基于余弦翘曲位移函数的薄壁箱梁剪力滞效应分析

宋爱明，李志聪，周 鹏，万 水，苏 强

(1.盐城工学院 土木工程学院，江苏 盐城 224051； 2.东南大学 交通学院，江苏 南京 211189； 3.河北省交通规划设计院，河北 石家庄 050011)

0 引言

薄壁箱梁以其自重小、跨越能力大、抗弯和抗扭性能强等诸多优点在桥梁建设中得到广泛使用[1]。当箱梁桥采用较大的腹板间距和悬挑长度时，恒载、活载、预加力等均会在结构横截面上引起显著的剪力滞效应[2]。翼板剪切变形是薄壁箱梁产生剪力滞效应的本质原因，受到对称荷载时，由于箱梁顶、底板发生剪切变形，剪力流在横向传递过程呈现滞后现象，使得横截面上的翼板拉应力不再均匀分布，这时按照初等梁理论的平截面假定不再适用。当板肋交界处的法向弯曲应力高于(或低于)横截面翼板中部应力时，即产生正剪应力滞效应(或负剪应力滞效应)。在国内外箱梁结构设计和建造史上因不考虑剪力滞效应而发生的结构破坏事故不在少数[3]，因此近些来，学者们针对箱梁剪力滞问题开展了一系列的试验研究[4]、理论解析[5]和有限元分析[6]。

能量变分法作为计算箱梁剪力滞效应行之有效的近似计算方法，由REISSNER[7]在1946年最先提出，其以矩形截面的薄壁箱梁为研究对象，并假定纵向翘曲位移沿箱梁截面横向按二次抛物线的线型分布。ZHANG[8]等基于二次抛物线型翘曲位移函数，分析了计入剪力滞效应的结构附加变形，继而以该附加变形为广义位移，提出了剪力滞效应的改进分析方法，并对翘曲函数的阶数精度进行了评价，最后采用有机玻璃模型试验对理论解析结果进行了试验论证。郭金琼[9-10]等国内研究者基于REISSNER的研究成果，分别将二次抛物线型翘曲位移函数变换为三次和四次抛物线的形式，进而对薄壁箱梁的剪力滞问题做了较为深入的理论解析和试验论证。倪元增[11-12]等研究者最早将余弦函数形式引入到剪滞翘曲位移函数中，并分别以槽型截面和箱形截面梁为研究对象，验证了采用余弦函数进行剪力滞效应分析的合理性和准确性。总的来说，翘曲位移函数的合理选择是基于能量变分法的薄壁箱型梁剪力滞效应分析的重点，目前采用多次抛物线型纵向翘曲位移函数的文献颇多，而采用余弦函数形式的文献较少。此外，学者们的研究成果在理论应用和指导设计方面具有重要意义，但在求解控制微分方程时往往为了简化计算方法而在箱梁各翼板间取一致的纵向位移差值函数，这样的简化方法忽略了各翼板因受力不同而产生的变形或剪力滞差异，与真实结构相比显然有所不符。

鉴于此，本文将选取余弦函数为薄壁箱型梁翼板剪滞翘曲位移函数，通过在横截面不同翼板处分别引入剪切转角最大差值u1(x)、u2(x)和u3(x)(即对应底板、顶板和悬臂板3个位置)，建立二阶常系数非齐次线性方程组，进一步求解得到薄壁箱梁任意截面法向弯曲应力以及无剪力滞效应时横向荷位的计算公式，并通过有限元分析软件ANSYS对受对称均布荷载作用下的简支箱梁进行数值分析，与本文理论计算结果进行对比验证。

1 基本假定

选取图1所示的薄壁箱型梁横截面为分析对象，坐标原点设置在截面形心位置处，箱梁体系的纵向、横向以及竖向分别对应坐标轴的x、y以及z方向。在箱梁顶板的某处(y0点)作用有z轴方向的荷载，分别引入不同翼板处的3个剪切转角最大差值函数ui(x)(i=1，2，3，下标i分别对应底板、顶板和悬臂板三个位置)，并且采用余弦函数形式来表示纵向位移ui(x，y)(i=1，2，3)沿箱梁横向的分布特征，那么不同翼板处的纵向位移有如下形式：

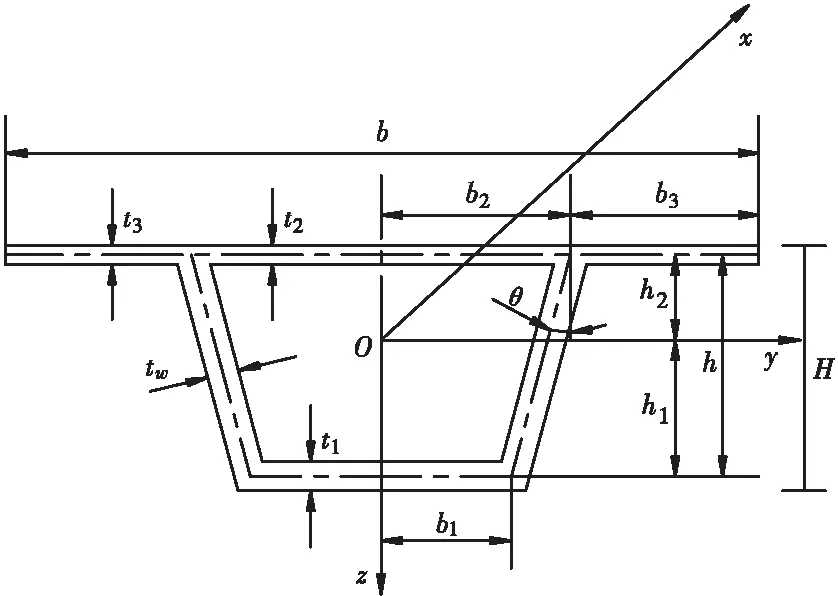
图1 箱梁横截面尺寸示意图

(1)

式中：w(x)是梁肋位置处的z轴方向挠度；h1、h2和h3是形心位置处与各翼板中轴线之间的距离；b1、b2和b3分别是各翼板的半宽。

假设箱梁截面在变形后仍与x轴方向的纤维相互垂直，那么翼板在x轴方向的变形ui(x)和z轴方向的变形Wi(x，y)可建立下述关系：

(2)

那么考虑横向位置(y方向)影响的z轴方向变形也可表述为按余弦函数分布的形式，如下式所示：

(3)

式(1)和式(3)是坐标x和y的连续函数，符合变形协调关系。在本文分析中有以下的假定：在计算截面应变时忽略剪切变形的影响，箱梁腹板仍遵循平截面假定；假定箱梁截面翼板z轴方向的纤维不发生挤压行为，那么有εz=0；此外，不考虑箱梁截面翼板、腹板等板平面外的横向应变及剪切变形，那么有γxz=γyz=εy=0。

2 微分控制方程的推导

根据最小势能原理，当受到外部荷载作用时，结构体系处于平衡状态。产生虚位移时，结构体系的总体能一阶变分为零，那么可记为：

(4)

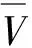
当有外部荷载作用于顶板时(0≤|y0|≤b2)，薄壁箱梁受弯曲而产生的外力势能可表述为：

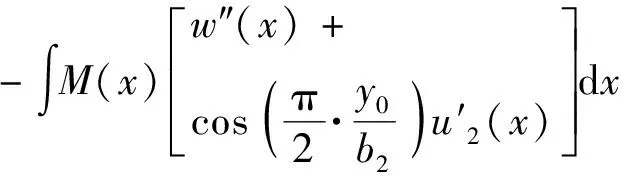
(5)

结构各部位应变能表达式分别为：

梁肋：

(6)

翼板：

(7)

式中：E、G分别为结构的弹性模量和剪切模量；t1、t2和t3为各翼板的厚度。

根据弹性力学平面问题的几何方程有：

(8)

将式(1)代入式(8)得到如下形式：

(9)

把上述式(8)和式(9)代入各翼板应变能表达式(7)可得到如下形式：

(10)

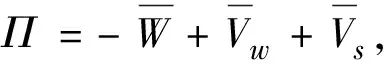
(11)

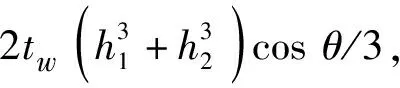
将式(11)得到的薄壁箱梁体系总势进行变分求解，并令其等于零，即δΠ=0，得到如下控制微分方程组：

(12)

其边界条件为：

(13)

3 二阶微分控制方程组的求解

上述内容根据能量变分法推导出了基于余弦翘曲位移函数的控制微分方程组，本节将对其进行求解分析。将式(12)中第一个等式对变量x进行求导并整理得到如下形式：

(14)

将式(14)代入式(12)其它3个微分控制方程可得：

(15)

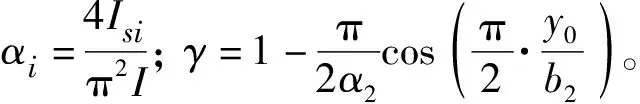
将方程组(15)转变为矩阵形式：

Au″-Bu=β

(16)

为方便推导，记：

C=A-1B；t=A-1β。

那么，则式(16)可转化为如下形式：

u″-Cu=t

(17)

计算A-1得：

(18)

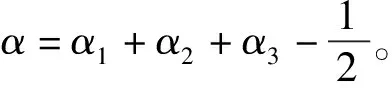
则有：

(19)

(20)

式(17)为二阶常系数非齐次线性微分方程组，根据文献[13]，得到该微分方程组的通解形式为：

U(x)=V[exp(-Λx)C′1+exp(Λx)C′2]

(21)

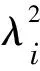
令u*为上述二阶常系数非齐次线性方程组的特解，该解只和结构剪力M′(x)的分布形式有关，那么进一步得到该方程组的通解表达式如下：

u(x)=V[exp(-Λx)C′1+exp(Λx)C′2]+u*

(22)

4 箱梁结构翼板中的应力计算

以上通过微分方程组解出了薄壁箱梁翼板剪切转角的3个最大差值式(22)，从而可进一步得到箱梁任意截面翼板各部分法向弯曲应力表达式为：

(23)

本文采用图2所示承受对称均布荷载的简支梁为算例，基于上述理论分析来进一步推导箱梁截面底板、顶板及翼缘板法向弯曲应力的表达式。

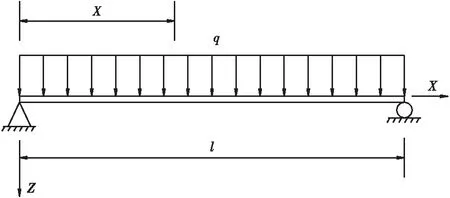
图2 简支梁承受均布荷载

箱梁任意截面x处的内力为：

x截面处的剪力是x的一次多项式，则微分方程组有特解：

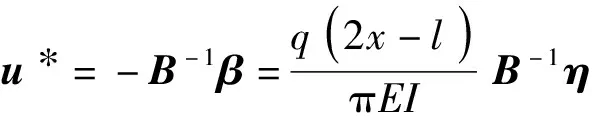
(24)

将式(24)代入式(22)并对变量x求导得到：

u′=VΛ[-exp(-Λx)C′1+exp(Λx)C′2]+

(25)

简支梁结构的边界条件为：u′i|x=0=0，u′i|x=l=0，则解得：

(26)

那么，可进一步由式(1)、式(23)和式(25)联合求解，得到对称均布荷载下简支箱梁结构截面弯曲法向应力表达式为：

(27)

5 算例分析及横向荷位确定

采用图2所示的单室梯形简支梁结构为算例来分析翼板各部位在采用余弦翘曲位移函数时，荷载横向作用位置(文中简称为：横向荷位)对剪力滞效应的影响规律。

a.箱梁截面采用图1所示形式，满跨对称作用均布荷载q=8 kN/m，材料及截面具体参数取值如下：泊松比ν=0.2，混凝土弹性模量E=3.5×104MPa，剪切模量G=E/(2+2ν)=1.46×104MPa；跨度l=40 m，腹板厚度tw=50 cm，腹板与翼板夹角θ=14°，翼板各部分厚度及宽度(半宽)分别为t1=50 cm，t2=t3=30 cm，b1=206.5 cm，b2=b3=300 cm，上板宽b=1 200 cm，箱梁高度H=415 cm，上下板壁厚中心距离h=375 cm，上板底至下板顶距离h′=335 cm。

上翼板壁厚中心面积矩按下式计算：

截面面积为A，则形心至上翼板壁厚中心的距离h2=S/A=160.11 cm，形心至下翼板壁厚中心距离h1=h-h2=214.89 cm。

其他参数计算结果如下：Iw=4.536 9 m4,Is1=9.535 5 m4,Is2=4.614 5 m4,Is3=4.614 5 m4,I=23.301 4 m4，α1=0.165 9,α2=0.080 3,α3=0.080 3,α=-0.173 5。

b.根据初等梁理论，薄壁箱型梁在任意截面上的应力计算方法如下：

(28)

取薄壁箱梁的跨中截面顶板为研究对象，那么截面弯矩为M(x)=ql2/8，则按式(28)得出σ1=0.147 6 MPa，σ2=σ3=-0.109 9 MPa。

当均布荷载对称作用于梁肋，即y0=b2，由数学软件分析MATLAB按式(27)解得：σ1x=0.155 5 MPa，σ2x=σ3x=-0.115 5 MPa，此时跨中梁截面表现为正剪力滞效应；当均布荷载对称作用于翼板中心，即y0=0，由MATLAB解得：σ1x=-0.001 8 MPa，σ2x=σ3x=-0.010 0 MPa，此时跨中梁截面表现为非常明显的负剪力滞效应现象；因此当均布荷载对称作用于梁肋与翼板中心之间，顶板上一定存在横向荷位y0=e，使得梁截面上σi=σix，即不产生剪力滞效应，这与文献[14]所得规律相似，说明本文方法具有可行性。为解得该横向荷位e，令：

U′=[U′1U′2U′3]T=

VΛ[-exp(-Λx)C′1+exp(Λx)C′2]

(29)

令σi=σix，且y=bi(i=3时，y=b2)，则可以解得式(30)：

(30)

当e

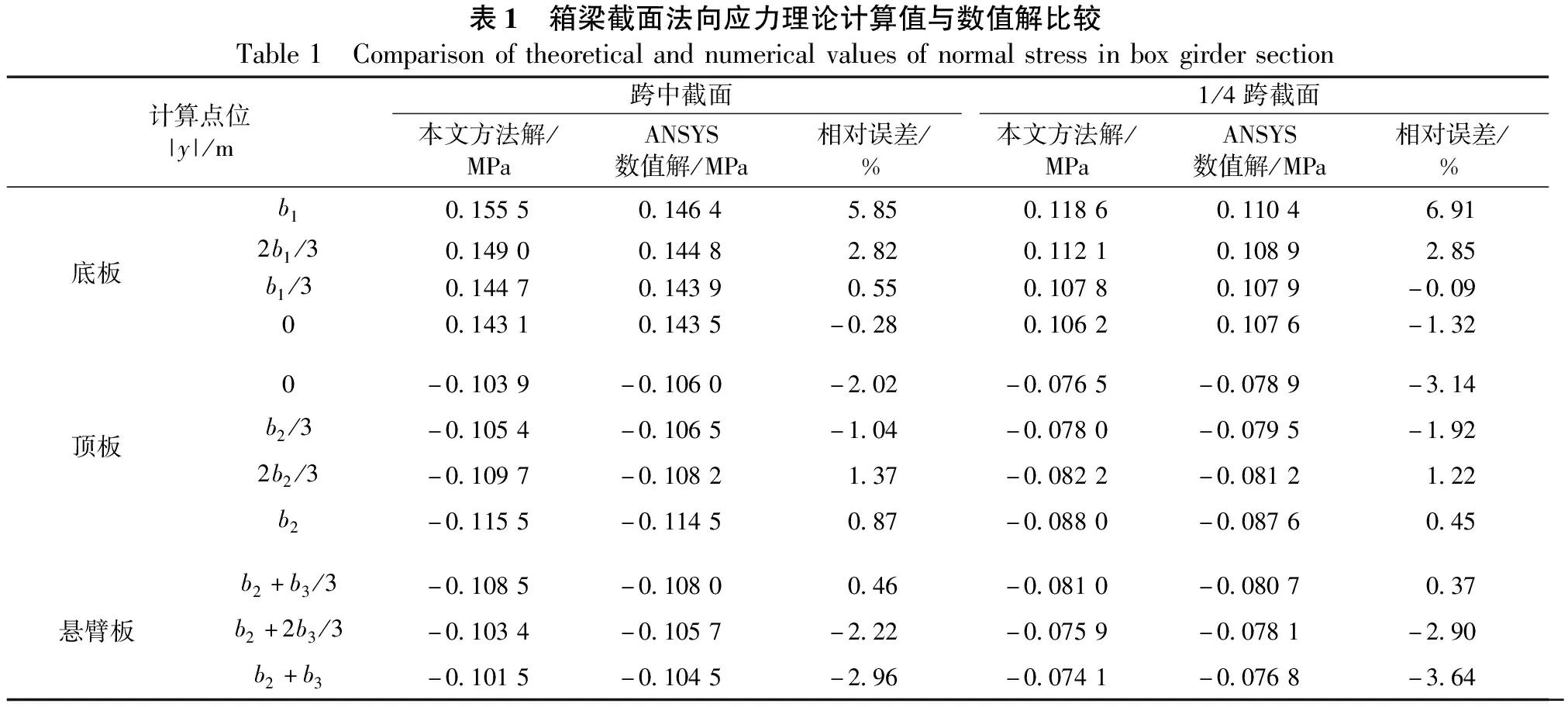
6 有限元数值分析

对上述算例通过ANSYS有限元软件进行数值模拟，对称均布荷载作用于梁肋处(即y0=±b2)。为保证计算结果的准确性，采用精度较高的六面体单元solid65来模拟全梁结构；箱梁一端支座处约束水平及竖直向位移，另一端约束竖直向位移；整个模型采用映射网格划分方式，单元数共计42 880个，计算模型如图3所示。

图3 箱梁有限元模型

采用本文方法计算得到的理论解与ANSYS数值解的对比结果列于表1，底板、顶板和翼缘板上各计算点位|y|均取自各板截面中心轴线上。

由表1数据分析可知，除了计算点位|y|=b1，通过本文方法得到的其它各点位的弯曲应力与ANSYS数值解误差均小于4%；计算位置|y|=b1处于腹板和底板交界点附近，腹板传递的剪力流在该点引起的剪切变形较为复杂，从而导致理论解与数值解之间的误差大于其它各点，在跨中和1/4跨截面分别达到了5.85%和6.91%。但总体来看，本文所采用的基于余弦翘曲位移函数的剪力滞效应变分解析方法与有限元数值解能够较好地吻合，表明本文方法具有一定的准确性，可为该类型桥梁结构的设计、分析提供理论依据。

表1 箱梁截面法向应力理论计算值与数值解比较Table1 Comparisonoftheoreticalandnumericalvaluesofnormalstressinboxgirdersection计算点位|y|/m跨中截面1/4跨截面本文方法解/MPaANSYS数值解/MPa相对误差/%本文方法解/MPaANSYS数值解/MPa相对误差/%b10.15550.14645.850.11860.11046.91底板2b1/30.14900.14482.820.11210.10892.85b1/30.14470.14390.550.10780.1079-0.0900.14310.1435-0.280.10620.1076-1.320-0.1039-0.1060-2.02-0.0765-0.0789-3.14顶板b2/3-0.1054-0.1065-1.04-0.0780-0.0795-1.922b2/3-0.1097-0.10821.37-0.0822-0.08121.22b2-0.1155-0.11450.87-0.0880-0.08760.45b2+b3/3-0.1085-0.10800.46-0.0810-0.08070.37悬臂板b2+2b3/3-0.1034-0.1057-2.22-0.0759-0.0781-2.90b2+b3-0.1015-0.1045-2.96-0.0741-0.0768-3.64

7 结论

本文通过引入余弦翘曲位移函数分析了薄壁箱梁剪力滞效应的变分解析方法，并进行了算例分析和有限元验证。主要结论有：

a.假设箱梁翼板剪滞翘曲位移函数为余弦函数形式，并分别引入顶、底板和悬臂板的剪切变形最大差值，建立了薄壁箱梁体系总势能函数表达式，应用变分原理推导出3个微分控制方程，通过对二阶常系数微分方程组的求解，得到了薄壁箱梁任意截面位置顶、底板以及悬臂板法向弯曲应力的计算公式。

b.以单室梯形截面简支梁结构为算例，分析了翼板各部位采用余弦翘曲位移函数时，荷载横向位置对剪力滞效应的影响，并进一步给出了箱梁截面无剪力滞效应时横向荷位的计算方法。

c.通过有限元分析表明，按照本文方法得到的箱梁截面弯曲应力理论解与数值计算结果吻合度较高，验证了其准确性。