不可靠网络环境下的网联汽车队列稳定性仿真分析

郭 迎，宋晓鹏，梁睿琳

（1.长安大学，陕西西安 710064；2.浙江数智交院科技股份有限公司，浙江杭州 310031）

车辆队列技术通过在车辆上安装传感器、雷达以及车载通信单元，使得车辆之间能够相互感应或通信，进而通过特定控制策略使多车辆排成一列，并保持一定的安全距离。该技术能够实现多车辆以相对较高的平均速度以及较短的跟驰间距安全行驶，提高了交通安全性与交通效率[1]。但车载无线通信的可靠性与许多不确定的因素有关，例如电磁波的多径效应、交通流密度、电子噪声、建筑遮挡、隧道和绿色植被等，并且当存在通信延迟时，车辆队列的速度及间距误差将沿着队列下游的方向放大，造成车辆队列的性能急剧下降[2]。

实车测试环境下的无线信道易受外界各种无线电信号干扰的影响，目前的仿真是国内外研究机构对于车辆队列性能的测试评估的重要技术手段。一些研究人员已经意识到通信延迟对车辆队列稳定性的影响，一部分研究人员通过改变网络配置来抑制通信延迟，从而达到提高车辆队列稳定性的目的。文献[3]提出了一种通过使用领导车辆和跟随车辆的预期信息来减轻车辆队列之间通信延迟的策略。文献[4]设计了一种策略，通过提供灵活的Ad-hoc 链接来减轻各种流量情况下的通信延迟。一部分研究人员通过设计更有效的队列控制器或跟车控制策略，例如文献[5]将车辆队列当作受时变异构通信延迟影响的动态网络，提出了一种缓解车辆队列稳定性问题的共识策略。还有基于图论推导了分布式控制协议，例如文献[6]在考虑时变通信延迟的基础上，提出了一种跟车控制策略，推导并证明了在频域内保证局部稳定性的充分必要条件以及保证串行稳定性的充分条件。此外，文献[7-9]为了处理通信和寄生延迟，将车辆队列建模为在各种时变网络拓扑下的多重延迟线性系统，研究了内部稳定性和串行稳定性，提出了一种自适应控制法和一种共识方法，旨在减轻通信延迟的影响。

通过对不可靠通信条件下的车辆队列稳定性的研究分析发现，目前研究人员在设计车辆编队行驶策略过程中，已经考虑到了通信延迟对于车辆队列稳定性的影响，但是始终缺少对车辆延迟环境下车辆队列稳定性表现的系统研究。针对上述问题，文中选取协同式自适应巡航控制系统(Cooperative Adaptive Cruise Control System，CACC)[16]作为车辆队列纵向控制策略，首先提出了一系列用于分析车辆队列状态的测试评价指标，包括速度、速度误差、间距误差以及实时车头时距等，然后在构建的仿真平台上，以“正弦振荡”为典型测试场景，仿真测试分析了在不同通信延迟环境下的车辆队列的稳定性。

1 网联汽车CACC控制策略分析

CACC 模式下工作的同质性车辆队列如图1 所示，其中di(t)是车辆i与其前一辆车i-1 之间的距离。di+1(t)是车辆i+1 与其前一辆车i之间的距离；vi+1(t)、vi(t)和vi-1(t)分别是车辆i+1、i和i-1 的速度；vi(t)⋅td+Gmin是车辆i和之前的车辆i-1 之间的期望间距[10]。

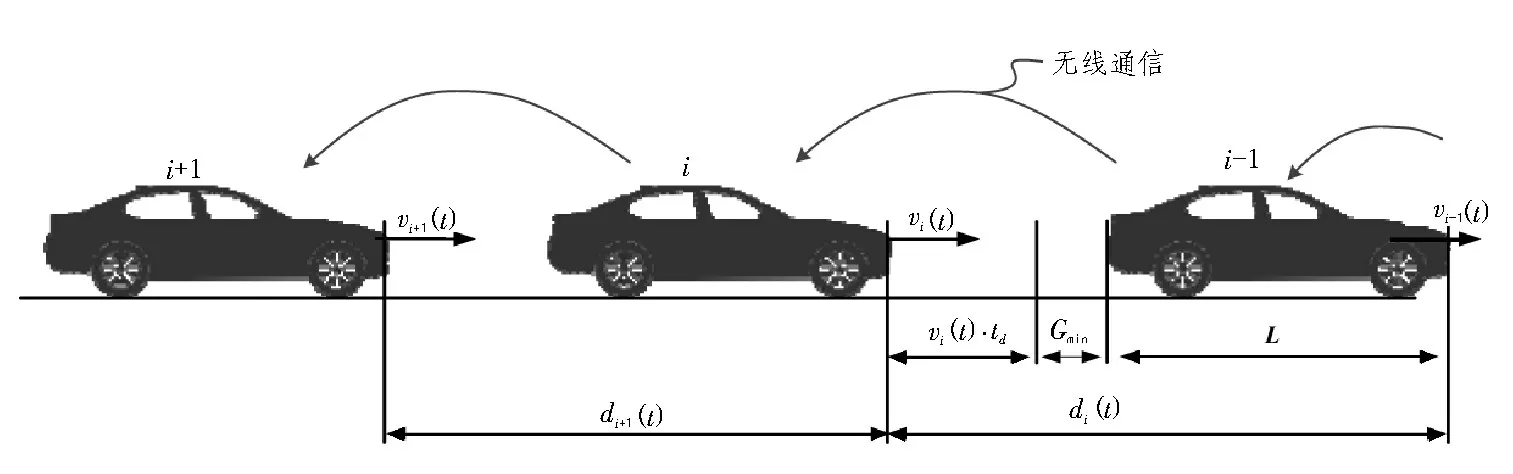
图1 同质性CACC车辆队列示意图

为了简化研究，文中使用单前继跟随（Single Predecessor Following,SPF）拓扑跟随车辆通过无线通信接收前方车辆的加速度信息，但仅识别并使用其最近的前方车辆的加速度[11]。尽管在实际情况中通信延迟是变化的，但是对于小范围内的同质性车队而言，文中认为车辆之间信道传输的通信延迟是相同的，即通信延迟的变化是整体的变化。

基于通用线性CACC 控制策略，文中选定恒定时距（Constant Time Gap,CTG）策略来讨论通信延迟边界[12]。引入通信延迟的控制策略如式（1）所示。需要注意的是，文中仅考虑前车加速度的通信延迟，并假设相对速度和间距等雷达探测信息不存在延时情况，基于上述假设可以集中讨论车联网环境下无线信道的通信延迟对车辆队列稳定性的影响。

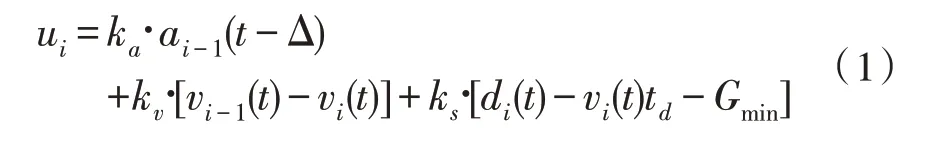
其中，ka是前车的加速度增益，kv是前方车辆i-1 与当前车辆i速度之差的增益，ks是前方车辆i-1与当前车辆i间距与期望间距之差的增益，Δ 是通信延迟项，di(t)是前方车辆i-1 与当前车辆i的间距，Gmin是车辆安全静止距离，td是CTG 策略当中定义的车头时距参数。CTG 控制策略的参数选取应满足车辆队列稳定性的要求。

2 仿真测试平台搭建

文中选用Plexe[13]仿真平台进行车辆队列稳定性的仿真测试与分析，并在该平台上进行二次开发，加入了采用CTG 策略的CACC 控制器，并进行了充分的调试以满足实验要求。Plexe 实际上是Veins[14]项目的扩展，目的是能够进行逼真的车辆队列仿真，同时Plexe 具有逼真的车辆动力学特性和多种巡航控制模型，可以分析车辆控制系统、大型交通流、混合交通流、车联网协议性能和车辆协同测试。Veins 依赖于两个模拟器，即基于事件的网络模拟器OMNeT++和道路交通模拟器SUMO。Veins 提供了一个Python 程序，以通过TCP 套接字连接将OMNeT++和SUMO 关联起来，从而对其进行扩展，以提供用于车辆间通信仿真的综合模型套件。

2.1 仿真环境及网络参数配置

文中选用的仿真环境是Plexe 2.1（基于Veins 4.7 拓展）、OMNeT++5.1.1 和SUMO 0.32.0，DSRC 设备的MAC 和PHY 层均基于IEEE 802.11p 标准，工作在5.89 千兆赫频段，带宽为10 MHz，数据传输速率设置为广播的最大值（IEEE 802.11p 中为6 Mbit/s），传输功率设置为100 mW，接收器灵敏度设置为-94 dBm。为了更好地模拟真实路网环境下的无线信道环境，使用弗里斯自由空间路径损耗传播（FPSL）模型，其中指数α的值设为2.0，信标的大小设置为200 字节，信标的发送频率设置为10 Hz，信标的优先级设为3。表1 汇总了仿真中所有的网络参数设置细节。

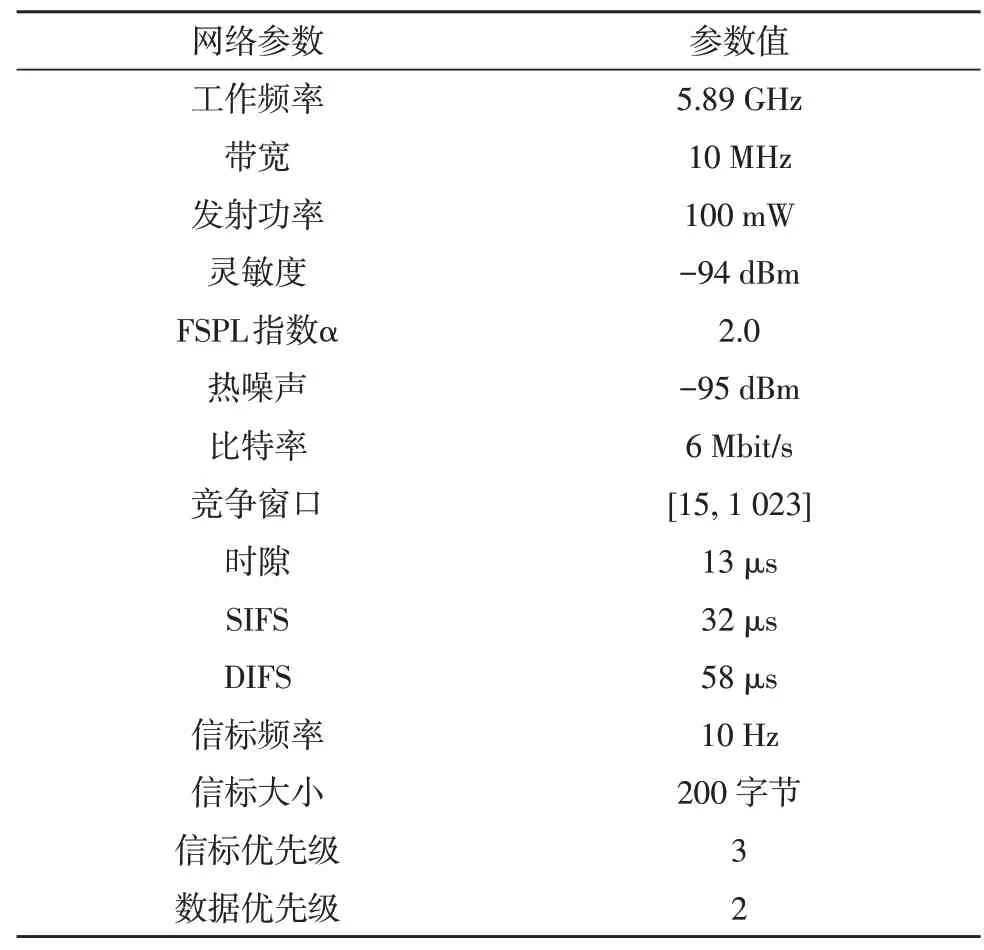
表1 网络参数设置

2.2 测试评价指标

为了仿真分析不可靠通信条件下的车辆队列稳定性及通信延迟边界，需要对仿真测试结果进行记录和分析。文中选取了一系列测试评价的指标，这些指标包括最基础的每辆车的速度，以及与车辆队列稳定性密切相关的速度误差、间距误差和实时车头时距。其中，速度误差是指前方车辆与后方车辆之间的速度差；间距误差是指实际跟驰间距与期望间距之差；实时车头时距是指车辆队列在行进过程中的动态车头时距。

1）速度。速度是车辆队列运行状态最直观的体现，通过观察车辆队列中每一辆车的实时速度变化，可以大致观测出车辆队列跟驰的效果优劣，但速度与车辆队列的稳定性之间没有直接的联系，因此还需要其他的评价指标。

2）速度误差(Speed Error,SPEE)。SPEE 定义如式（2）所示，车辆i的速度误差意为当前车辆的期望车速（在车辆队列中即最近前车的车速）与其车速之差。若速度误差沿着车辆队列下游递减/收敛，认为该车辆队列的状态是稳定的；相反，若速度误差沿着车辆队列下游递增，则认为该车辆队列的状态是不稳定的。

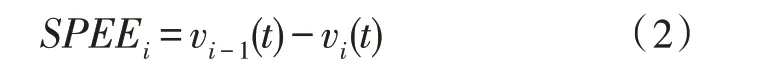
3）间距误差(Spacing Error,SPCE)。SPCE 定义如式（3）所示，车辆i的间距误差意为当前车辆与最近前车的距离减去期望间距。若间距误差沿着车辆队列下游递减/收敛，则认为该车辆队列的状态是稳定的；相反，若间距误差沿着车辆队列下游递增，则认为该车辆队列的状态是不稳定的。

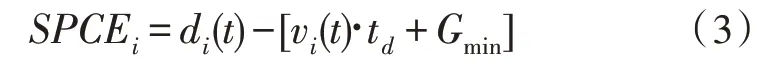
4）实时车头时距。此处实时车头时距是仿真过程中动态变化的车头时距，不难发现，实时的车头时距会在文中设置的期望车头时距上下振荡，其振幅的大小也反映了车辆队列稳定性的优劣，振幅越小表示稳定性越好。

3 测试场景构建

在仿真验证中设置了“正弦振荡”场景。该场景是车辆在高速公路上成群行驶时的典型场景，如图2所示。构建一个由一辆头部车辆与五辆其他车辆组成的车辆队列，在高速公路上的一个车道内行驶，并且六辆车的配置完全相同。在“正弦振荡”场景中，对车辆队列头部车辆进行速度配置，包括加速、巡航和制动过程。

图2 “正弦振荡”场景示例

在表1 中网络参数设置的基础上，表2 新增了用于评估车辆队列稳定性的仿真参数，将执行器迟滞设置为0.5 s[15]，期望车头时距设置为1 s，并根据前文建立的通信延迟边界模型，将CTG 控制策略参数ka、kv和ks分别设置为0.6、0.4 和0.2，头部车辆的正弦振荡频率为0.04 Hz，振幅为10 km/h。

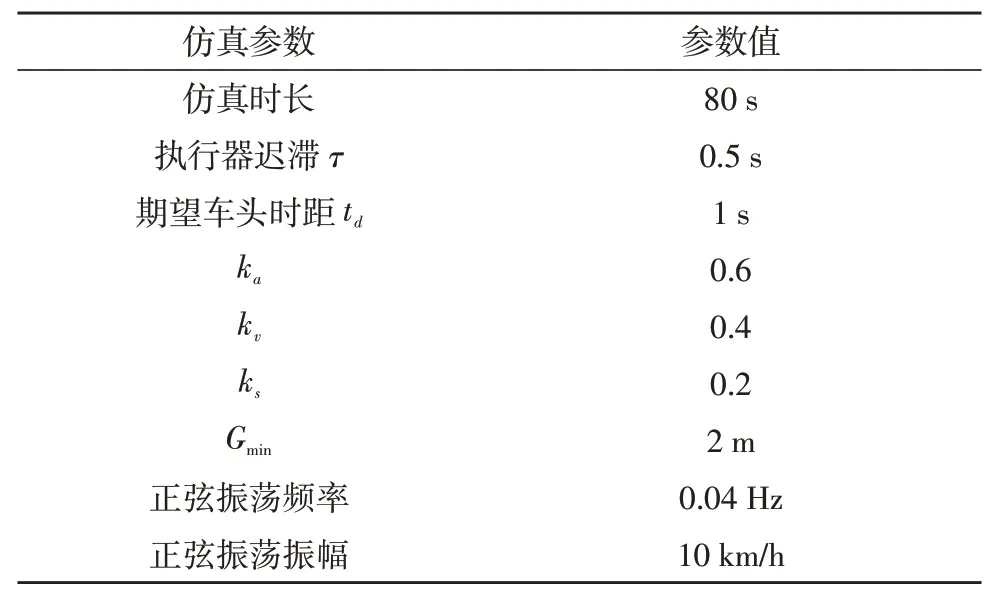
表2 仿真参数设置

在上述场景中进行仿真，首先头部车辆先以30 km/h 的速度巡航，并在第10 s 时开始进行正弦振荡，正弦振荡频率为0.04 Hz，研究表明，0.04 Hz 的干扰频率是运输流中的典型频率，正弦振荡的振幅为10 km/h，并一直保持到80 s 仿真结束。头部车辆的速度和加速度曲线如图3 所示。

图3 “正弦振荡”场景中领导车辆的速度和加速度曲线

4 仿真测试与分析

根据前文提出的测试评价指标，对车辆队列在“正弦振荡”过程中的速度、速度误差、间距误差以及实时车头时距结果进行分析，为了更加直观地展示实验结果，选取了通信延迟在0 s（即没有延时）、0.2 s、0.5 s 的结果进行分析。

4.1 行车速度分析

如图4(a)所示，可以观察到在没有通信延迟的情况下，后续车辆的速度能够被限制在车辆队列上游的速度以内，并且当通信延迟达到0.2 s 时，仍然可以很好地限制后续车辆的速度，如图4(b)所示。然而，如图4(c)所示，当通信延迟较高时，不能很好地限制后续车辆的速度。值得一提的是，在图4(c)所示的速度数据的第一个峰值处，车辆队列的稳定性很明显受到了干扰，但在接下来车辆速度在第二高峰和第三高峰处又得到了限制，这是因为kv和ks项减轻了由前车造成的速度干扰。因此，后续车辆速度能够被控制在第二峰值处，但是这并不能表明车辆队列处于稳定状态，因为在第一个峰值处的速度放大足以引起车辆队列的不稳定，从而产生碰撞事故，此时车辆队列处于不稳定状态。

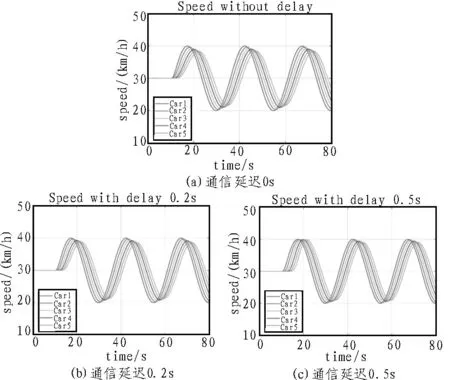
图4 不同通信延迟条件下车辆队列的速度

4.2 速度误差分析

车辆队列的速度误差信息如图5 所示，其中通信延迟分别为0 s、0.2 s、0.5 s。

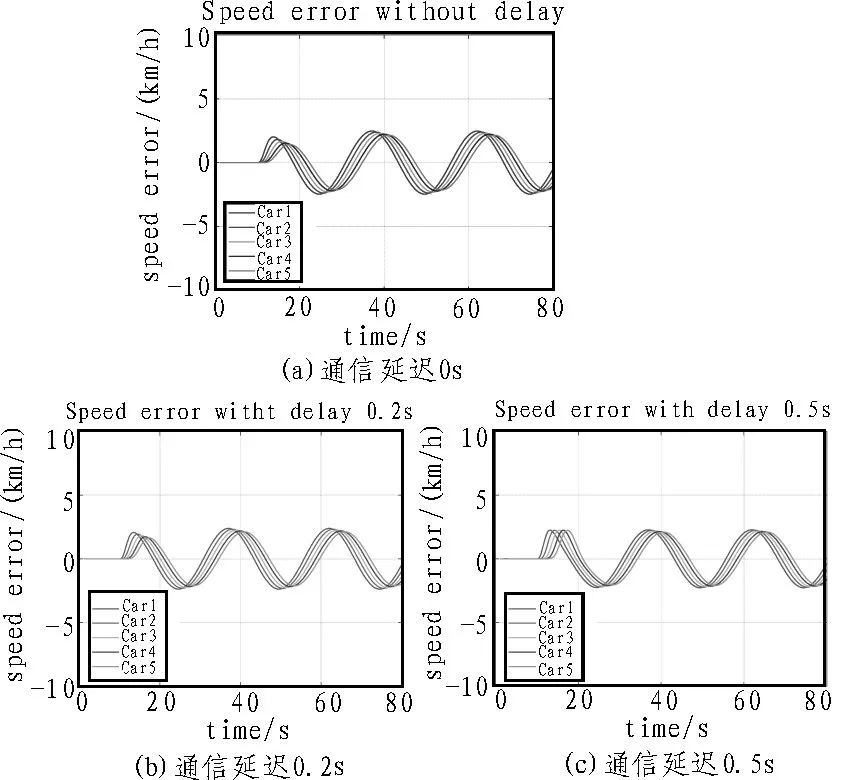
图5 不同通信延迟条件下车辆队列的速度误差

如图5 所示，速度误差的变化清晰地反映出了车辆队列的稳定性随着通信延迟的增加而恶化的情况。出于与上述相同的原因，以速度误差曲线的第一个峰值区进行分析，能够明显观察到，当无线传输信道没有通信延迟或只存在相对较小的延时时，后续车辆的速度误差会受到限制，如图5(a)和5(b)所示。但是，当通信延迟较高时，不能继续限制后续车辆的速度误差，即速度误差项会沿着车辆队列下游放大，如图5(c)所示，此时车辆队列处于不稳定状态。

4.3 间距误差分析

车辆队列的间距误差信息如图6 所示，其中通信延迟分别为0 s、0.2 s、0.5 s。

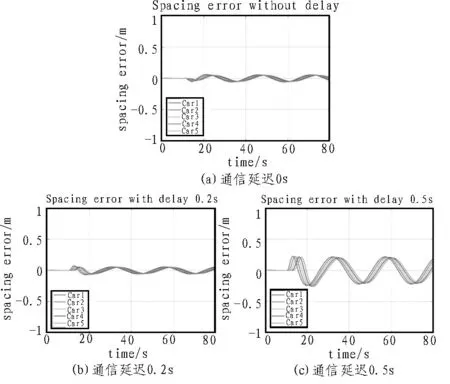
图6 不同通信延迟条件下车辆队列的间距误差

如图6 所示，间距误差的结果比速度误差更清晰地反映了车辆队列稳定性随着通信延迟的增加而恶化的情况，这是由于间距误差是速度误差积分的原因。可以观察到，当通信延迟较低时，车辆队列的间隔误差很小并且会在向下游传播时受到限制，如图6(a)和6(b)所示，这表明了车辆队列具有良好的稳定性。但是，当通信延迟到达其边界时，首先能够明显观察到，间隔误差的大小会显着增加；其次，与上述原因相同，在第一个波谷时，车辆队列的间距误差会沿着下游放大，如图6(c)所示，此时车辆队列处于不稳定状态，这表明较高的通信延迟不仅破坏了车辆队列的稳定性，而且还会威胁到交通安全。

4.4 实时车头时距分析

车辆队列的实时车头时距信息如图7 所示，其中通信延迟分别为0 s、0.2 s、0.5 s。

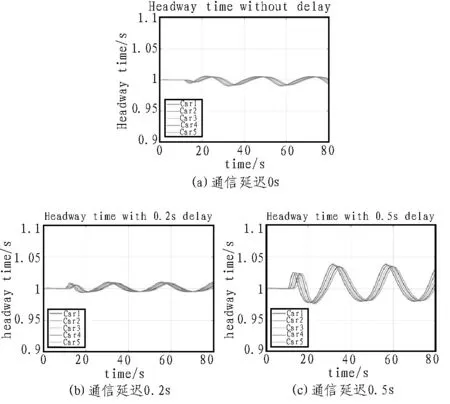
图7 不同通信延迟条件下车辆队列的实时车头时距

如图7 所示，从实时车头时距的变化中也能够得出与间距误差相似的结论。当通信延迟较低时，实时车头时距的振荡小且能够沿车辆队列下游收敛，但是当通信延迟较高时，实时车头时距的振荡会显著增大且在第一个波谷区域能够观察到振荡会沿着车辆队列下游放大，此时车辆队列处于不稳定状态[16-20]。

5 结束语

智能网联汽车是以C-V2X/DSRC 等车联网通信技术与自动驾驶技术融合落地应用的重要着力点，是全球创新热点和未来发展制高点。在众多典型应用中，智能网联汽车队列行驶被认为是最具代表的应用场景之一，预期将最快进行部署、应用。然而，基于V2X 技术构建的智能网联汽车队列极易受电磁波的多径效应、交通流密度、电子噪声、建筑遮挡、隧道和绿色植被等各种因素造成的通信延迟影响。文中针对上述问题，选取CACC 作为车辆队列纵向控制策略，提出了一系列用于分析车辆队列状态的测试评价指标，然后在构建的基于Plexe 仿真平台上，以“正弦振荡”为典型测试场景，仿真测试分析了在不同通信延迟环境下的车辆队列稳定性。仿真测试结果表明，通信延迟会在速度、速度误差、间距误差以及实时车头时距等方面对智能网联汽车队列造成显著影响。