高海拔环境下四旋翼无人机飞行姿态控制技术研究

高晗，颜世成

（中国南方电网有限责任公司超高压输电公司大理局，云南大理 671000）

四旋翼无人机在近些年的无人机领域中发挥着重要的作用，其具有驱动时间长、耦合性能好、抗干扰能力强等优势，大量地应用于军队与民间[1-2]。四旋翼无人机的飞行主要是通过调节4个旋翼的转速以及状态来完成起飞、斜飞、侧飞、盘旋等飞行姿态[3-4]。

在高海拔的环境下对四旋翼无人机的飞行姿态进行控制，更需要发挥其抗干扰与耦合性能强的特点，传统的对四旋翼无人机飞行姿态的控制技术主要是通过滑模算法以及PID 控制法实现[5]。滑模算法下对四旋翼无人机飞行姿态的控制主要是应用滑模算法的鲁棒性，当无人机的控制系统出现问题时，依靠鲁棒性体现出无人机的抗干扰能力强的性能，有效地降低四旋翼无人机的机身不平衡问题，对滑模的终端参数进行求导后出现的负指数项，能够引入积分项对四旋翼无人机的平稳性进一步增强，但是这种方法的参数精确度低，不能够精准地对干扰数据及时反馈，从而影响了对机身的姿态控制[6]。PID 控制法主要是通过对飞行姿态控制器的误差与变化率进行监测规划，用模糊算法引导飞行姿态控制器对无人机的机身控制，这种方法的实现方式比较简单，适用于简单的无人机模型控制，但是其应用在四旋翼无人机中需要具备过高的调控数据与相关资源，且模糊算法的参数运算语言精确度差，导致飞行姿态控制器对四旋翼无人机的姿态控制有较大的偏差[7]。

为了改善传统方法中存在的问题，文中将重新对高海拔环境下的四旋翼无人机飞行姿态控制技术进行研究。

1 飞行姿态控制动力模型

为了方便对高海拔下的四旋翼无人机飞行姿态控制技术的研究，文中将对四旋翼无人机的机身做出一定假设，统一性地对控制动力模型进行研究[8]。假设四旋翼无人机的机身不出现外形变形的状况，视四旋翼无人机为一个形态均匀的刚体；设四旋翼无人机的重心与机身在坐标系中的坐标点位置一致；设高原环境中的大地为坐标系平面，不考虑无人机在曲面的飞行路线；设四旋翼无人机在高海拔的环境中飞行气流与四旋翼的旋转状态呈正常关系[9]。四旋翼无人机结构示意图如图1 所示。

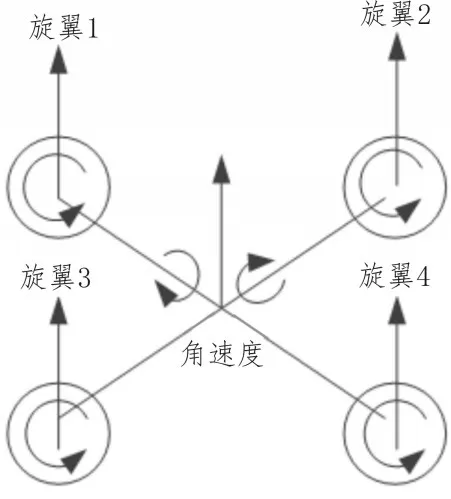
图1 四旋翼无人机结构示意图

四旋翼无人机的飞行姿态控制主要是依靠动力学理论实现，动力学理论的实现公式如下所示：

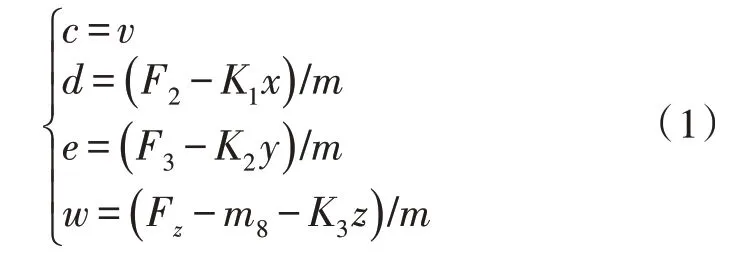
式中，k代表无人机飞行动力的阻力系数，F代表不同方向的运动气流，m代表飞行距离，v代表四旋翼无人机的飞行速度。四旋翼无人机的飞行过程中需要依靠多种角速度来代表无人机的非直线飞行状态，角速度的具体获取方法如下所示：

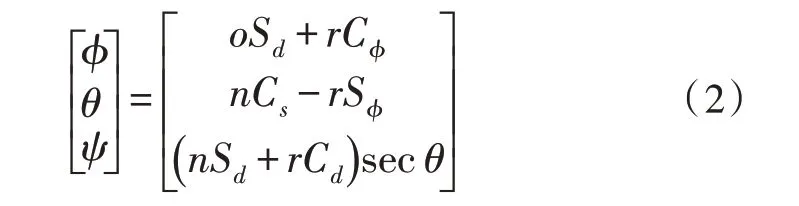
式中，ϕ、θ、ψ分别代表无人机在不同飞行姿态下的飞行角度，Sd、Cϕ、Cs、Sϕ、Cd分别代表四旋翼无人机的飞行控制器中发出的飞行姿态操作命令指令，o、n、r分别代表高海拔环境下的气流速度。可以应用四旋翼无人机的电机运行速度判断机身的飞行状态与角度，代入电机的运行速度进一步计算较精准的角速度，在忽略四旋翼无人机的其他干扰阻力时所获取的角速度与无人机的飞行速度呈非线性关系，方便引用动力相关原理[10]。

应用扰动动力原理来处理非线性关系，能够较好地控制四旋翼无人机飞行姿态变化过程中的较小扰动变量因素，使无人机的姿态变化在横向飞行和纵向飞行的整体变换范围内，都能够无视小扰动因素的影响，尤其是无人机在小角度运动的状态下可以视飞行姿态为滑行或悬停，认定飞行状态角度与加速度之间处于积分关系，受到角度的影响因素有限，设定扰动原理下的无人机姿态控制的状态变量为：

由式（3）可以看出，四旋翼无人机的飞行姿态变化角度控制主要是通过3 种飞行参数共同实现，同时也是无人机的飞行动力系统的理论组成部分，结合四旋翼无人机的耦合性与抗干扰性设计了高海拔环境下四旋翼无人机飞行姿态控制的动力模型[11-12]。

2 飞行姿态控制

高海拔环境下四旋翼无人机飞行姿态的控制需要有较敏感的数据反馈体系与数据运算体系。数据反馈体系主要是对飞行姿态的控制数据线性化处理，增强控制器对四旋翼无人机的控制精确度，增加飞行姿态控制器的可行性与精准性；数据运算体系主要负责对高海拔环境下的飞行数据与非线性动力数据进行运算并传输到控制器中，与反馈系统相互配合，实现更加精准的对四旋翼无人机飞行姿态的控制[13-14]。

文中数据反馈体系的设计主要是利用反馈的方法实现飞行数据的线性化，使控制器的指令输出与四旋翼无人机的飞行姿态信号接收呈线性关系，在动力模型中，高海拔环境下的驱动相关参数呈现非线性关系，反馈线性化原理虽然能够适应非线性关系的飞行数据，但是需要建立在控制器与无人机之间的通信信号的基础上，因四旋翼无人机的4 个旋翼均能够得到控制，所以控制器与无人机之间的参数传输属于一对多类型，并不符合反馈线性化的适应环境，为此，文中首先建设一套非线性参数系统作为状态变量的运算参考，运算的实现公式如式（4）所示。

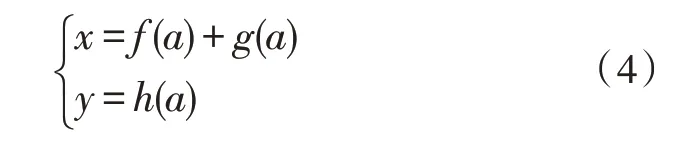
式中，x、y分别代表运算的参数状态变量，f(a)、g(a)、h(a)分别代表控制器的发送指令，指令信号包含角速度的大小、气流的方向与速度、空气阻力以及目前无人机的飞行加速度等[15]。

反馈体系中包含对飞行角速度与位移的反馈信息，这两种因素之间是相互独立的，非线性关系下的位移因素包含飞行状态的角度变化，而在反馈体系的线性关系下，文中选取角速度的精准运算程序作为四旋翼无人机飞行姿态控制器的指令发送主体。控制器的指令发送首先确定四旋翼无人机的滚角速度并对外输出，假设输出的指令信号定义为a，四旋翼无人机的跟踪指令接收信号误差为x，定义控制器对外的发送指令计算函数为：

若四旋翼无人机的跟踪指令接收信号无误差产生，则无人机的飞行姿态控制可以达到最精准状态[16]。进行其他指令的发送则需要实际控制其他参数系统中的数据以及外界干扰参数，由于不确定因素导致控制器对无人机的飞行姿态控制具有一定的不定时性与不确定性，因此在反馈体系中引入自律算法来规范不确定因素的产生，建立参数的线性关系，实现线性关系的定义公式如下：

式中，x代表其他指令中存在的参数误差。控制器在数据反馈体系下的结构框图如图2 所示。

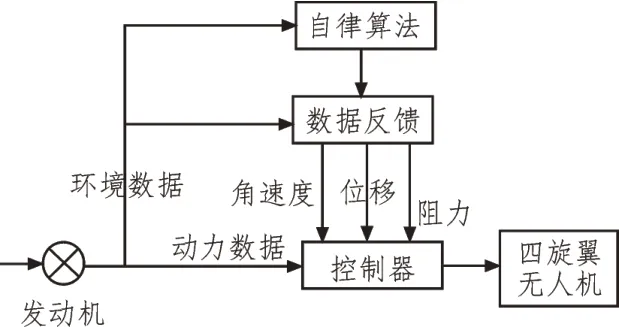
图2 控制器在数据反馈体系下的结构框图

随着参数误差的变化，控制器对四旋翼无人机飞行姿态的控制指令实现结果会产生不确定性偏差，为此，文中采用量化因子的方式改变误差的变化，使参数的误差随控制系统的数据变化而变化，在控制器的相关算法中加入伸缩因子，弥补控制器对参数误差的模糊计算。控制器中加入量化因子前后的指令效果对比图如图3 所示。

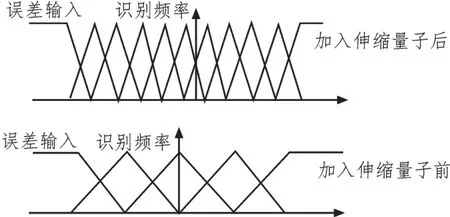
图3 控制器中加入量化因子前后的指令效果对比图

3 实验研究

对高海拔环境下的四旋翼无人机飞行姿态控制技术的传统实现方法主要有滑模算法以及PID 控制法。这两种传统算法虽然能够在高海拔环境中有较好的适应能力以及抗干扰能力，但是由于控制技术原因，导致这种两种算法在飞行姿态的识别度效果上有着较大的偏差，不能够精准地识别控制器发出的指令，导致四旋翼无人机飞行姿态的变换与控制器所发送的指令不同。且这两种传统算法的角度识别能力也较弱，导致无人机飞行姿态的变换不到位。而文中方法在这两方面均有所改善，为了验证该方法的有效性，设定实验对比3 种方法的相关结果。为了确保实验过程中不出现偶然性，该实验制定了实验参数，具体参数如表1 所示。

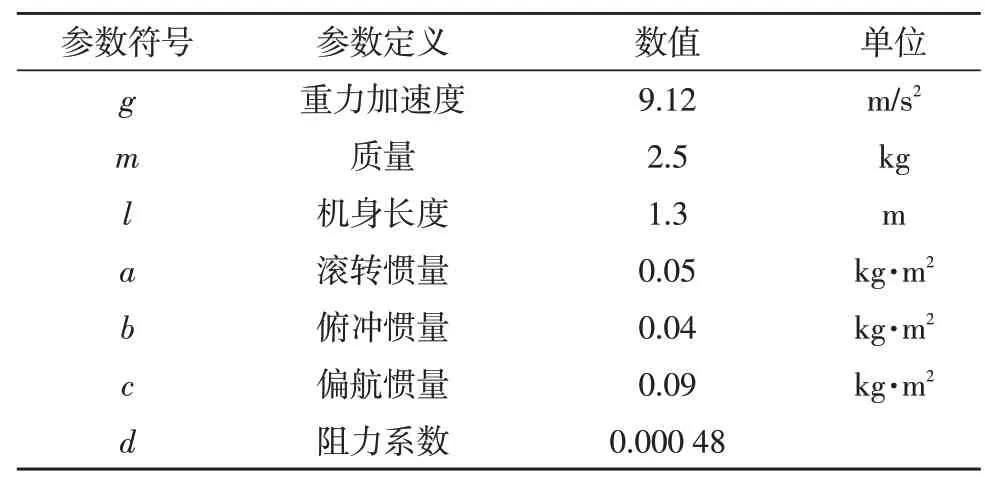
表1 实验参数表

实验过程中首先使四旋翼无人机处于悬停状态，此时的机身状态平稳，角速度、加速度、阻力等相关变量参数为零，文中方法下滚转角期望值为15°，俯仰角期望值为12°，偏航角期望值为23°，无人机的加速度为2 m/s2。四旋翼无人机的实验过程运行仿真角度如图4 所示。

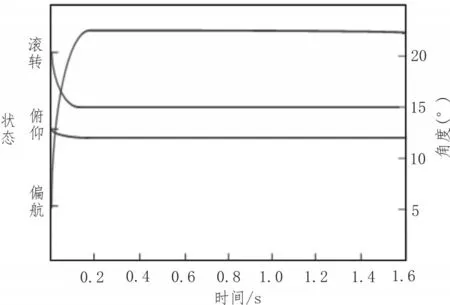
图4 四旋翼无人机的实验过程运行仿真角度

控制器在发送启动指令0.1 s 后，无人机的各个角度的姿态基本都能达到参考值范围，在2 s 后向控制器中添加一个脉冲信号，信号的内容为高压环境下的强风环境，控制四旋翼无人机进行滚转角姿态飞行，向控制器的指令算法中输入不连续的环境数据函数，抑制四旋翼无人机的高颤动作，使实验的运行效果更加稳定。在强风环境下，3 种方法下四旋翼无人机滚转角姿态飞行的姿态实现效果如图5所示。

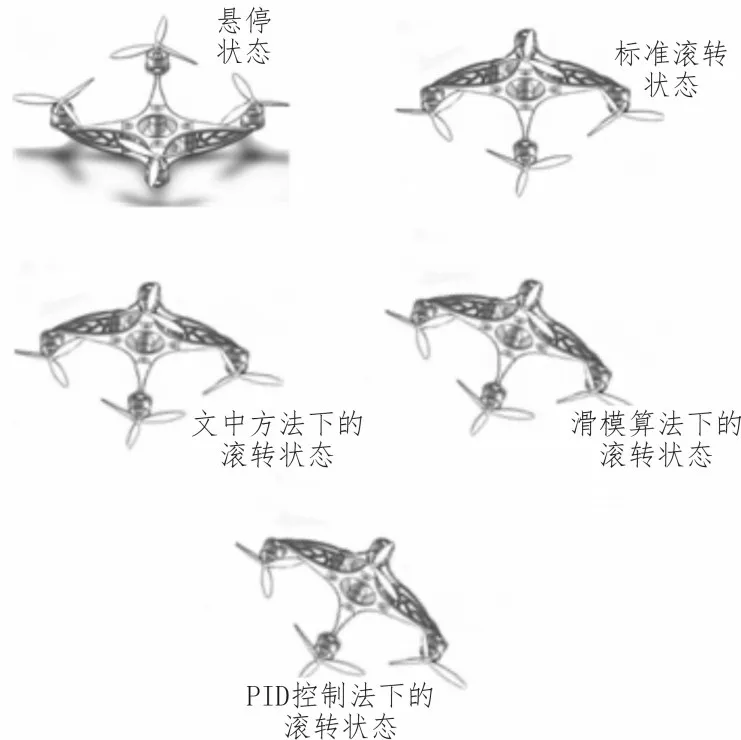
图5 3种方法下四旋翼无人机滚转角姿态飞行的姿态实现效果对比图

根据图5 可知，在文中方法控制下无人机的飞行姿态控制效果最明显，在控制器中输入反馈线性化体系以及相应的算法，能够对环境中的信息以及无人机的实时状态进行反馈处理，进而控制器能够在第一时间对四旋翼无人机的各个旋翼的旋转状态发送指令，更加有效地改变无人机的飞行姿态。而传统方法利用滑模终端的计算方式来判断环境数据，运算过程中的数据较为模糊，导致控制器发送的指令不具有实时性。

文中还对3 种方法下的无人机角度识别能力进行对比，结果如图6 所示。

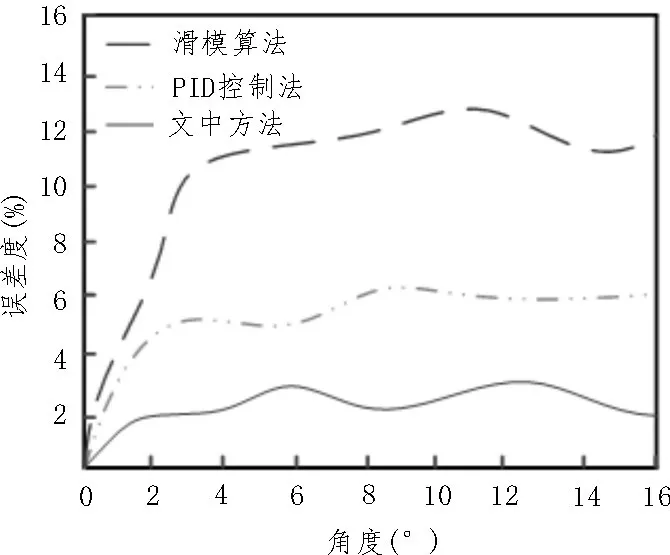
图6 3种方法下的无人机角度识别误差

根据图6 可知，文中方法下的无人机飞行姿态对角度的识别误差程度更低，引入了量化因子对控制器中的指令数据误差做出精准化处理分析，并以线性关系形式实现控制器的指令表达。而传统方法中主要采用模糊算法对角度数据处理分析，具有不精准性导致角度识别能力较弱。

4 结束语

文中针对高海拔环境下的四旋翼无人机飞行姿态控制技术进行研究，改变传统方法中存在的部分问题，分析动力模型在控制器中的作用并建立模型，在实现控制的过程中加入反馈线性化体系和数据运算体系，最终通过对比实验验证了该方法的有效性。