无证书的支持树形访问结构的属性基签名方案
邓银娟,杜红珍,马巧梅
(1.宝鸡文理学院数学与信息科学学院,陕西宝鸡 721013;2.宝鸡文理学院计算机科学学院,陕西宝鸡 721013)
在电子医疗档案系统中,传统的数字签名会造成用户身份信息泄露,从而给用户隐私带来威胁。属性基数字签名不仅可以保护签名者的身份信息,而且可以实现细粒度的访问结构。2005 年,文献[1]首次定义了基于属性的密码体制,该体制用一组属性集合定义用户。文献[2]中首次提出了属性签名ABS(Attribute-Based Signature)的概念,方案的提出是基于属性加密的,在该方案中访问结构为单层属性。属性签名在访问控制方面具有极好的优势,国内外学者们在其功能性、灵活性以及效率等方面提出了各种改进方案[3-8]。然而,这些属性签名所用私钥一般都由中心化的机构产生,从而会产生安全隐患。在无证书公钥密码体制中[9-14],签名者的私钥不完全由中心生成,签名私钥由KGC(Key Generate Center)和签名者共同生成,因此可以有效地解决上述问题。
为了实现安全灵活的访问控制,文中在分析现有树形访问结构属性签名的基础上,利用无证书签名技术,提出了一种新的无证书的属性基签名方案。该方案的创新点有:1)解决了属性公钥密码体系下固有的密钥托管问题,同时保留其不需要公钥证书的特性。2)对新设计算法的安全性进行了严格的数学证明,并且通过效率分析表明签名和验证过程仅使用一次双线性对运算,计算效率得到很大的提高。最后通过仿真实验,与效率较高的属性签名算法[4]比较,结果表明,该方案具有更好的签名和验证效率。
1 预备知识
1.1 双线性映射
双线性映射相关定义请参考文献[5]。
1.2 应用系统架构
电子医疗档案系统中用户更新信息的系统架构由4 部分组成:用户、用户中心、密钥生成中心、存储系统。应用系统架构如图1 所示。

图1 应用系统架构图
具体操作流程如下:
1)系统需要更新某类用户信息,下发该类用户的树形访问结构给KGC,并通知该类用户及时将信息上传到存储系统更新。
2)用户选择自己的签名公私钥对和传输公私钥对,并将传输公钥给KGC,申请用户的部分私钥,并验证公钥。
3)KGC 传输加密后的部分私钥给用户。
4)用户对自己要更新的信息进行签名,并将签名、要更新的信息以及用户属性集合发送给用户中心。
5)用户中心验证用户属性集合的逻辑合理性,并将签名、待更新的信息以及用户属性集合发送给存储系统。
6)存储系统验证签名,若签名验证通过,则更新用户信息。
1.3 秘密共享方法
秘密共享方法请参考文献[15]。
Case1:当τ为关系“or”时,令τ的每个子结点的值为s;
Case2:当τ为关系“and”时,τ的子结点数量为u,前u-1 个子结点为随机值,最后一个子结点为
Case3:当τ为关系“threshold”时,如果结点门限值为h,那么随机选择一个h-1次的多项式f(x),使得f(0)=s;索引次序为的子结点,取值为f(i)。
从根结点起,由上述法则为每个结点自顶向下、递归地赋值,最后完成所有叶结点的赋值。
1.4 秘密重组算法
由秘密共享办法定义一个与其可逆的递归算法Verify(Node),该算法对象Node是树形访问结构的各个结点,分情况处理如下[16]:
Case1:当Node结点不是叶结点,关系为“and”时,遍历此结点的所有子结点,并将所有子结点的返回值作乘积,结果为该结点算法的返回值;若存在一个子结点不满足要求,则返回验证失败;
Case2:当Node结点是非叶结点,关系是“or”时,遍历此结点的所有子结点,当遇到首个满足条件的子结点时,遍历停止,并且返回该子结点的值,即为此结点的验证值;若所有子结点都不满足要求,则返回验证失败;
Case3:当Node结点是非叶结点,关系为“threshold”,且门限值为h时,遍历此结点的所有子结点。当子结点中满足要求的个数大于或等于h时,选取其中h个结点,记集合为H,计算的值并返回;当子结点中满足要求的个数小于h时,返回验证失败。
Case4:当Node结点是叶结点,且叶结点的属性值满足i∈w时,返回σi,当i∉w时,返回⊥。
1.5 拉格朗日插值
定义1(拉格朗日插值)设f(x)是值域Zp上的一个h-1 次多项式,设元素个数为h的集合为S⊆Zp,那么可以通过下面公式求得f(x):
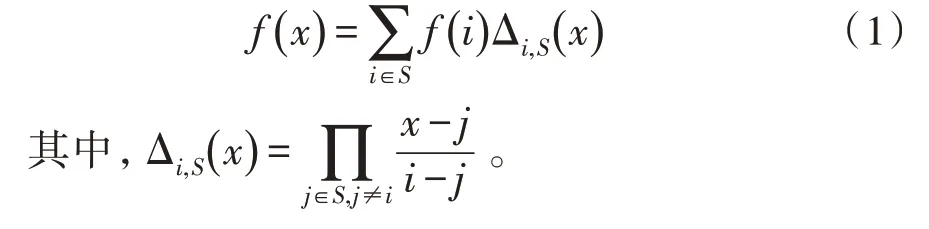
2 算法描述
1)系统建立阶段
setup(λ):输入安全参数λ,选取一个阶为q(q为大素数,且q>2λ)的加法群G1和乘法群G2,设g为G1的生成元。e:G1×G1→G2是一个双线性映射,H:{0,1}∗→为抗碰撞哈希函数,设属性集合为U={1,2,...,n} 。随机选取,并定义树形访问结构为T。参数定义如下:
params={g,G1,G2,e,H},MSK=y。
2)密钥值建立阶段
Set-Secret-Value(params):用户随机选取s,SKs=s为用户传输私钥,SKx=x为用户签名私钥,计算公钥PKs=gs,PKx=gx。
3)部分私钥提取阶段
Extract-partial-private-key(params,w,MSK,PKs,T):w为用户属性,MSK为系统主密钥,PKs为用户的传输公钥,MSK为共享秘密,由秘密共享方法将其赋值给树形访问结构的所有结点。设叶结点的属性集合为L,叶结点的赋值为{yi,i∈L},随机选取,则定义集合S={si,1 ≤i≤n},其中:
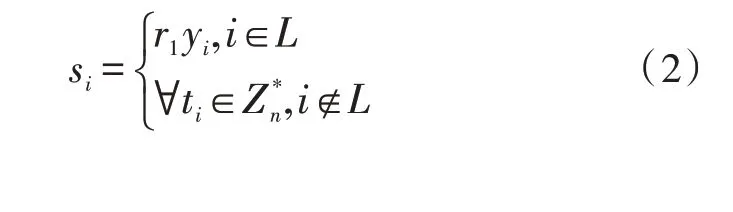
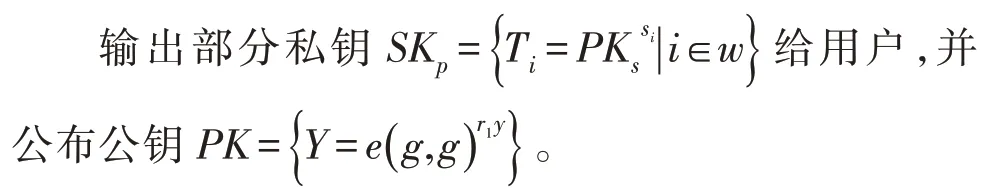
4)私钥建立阶段
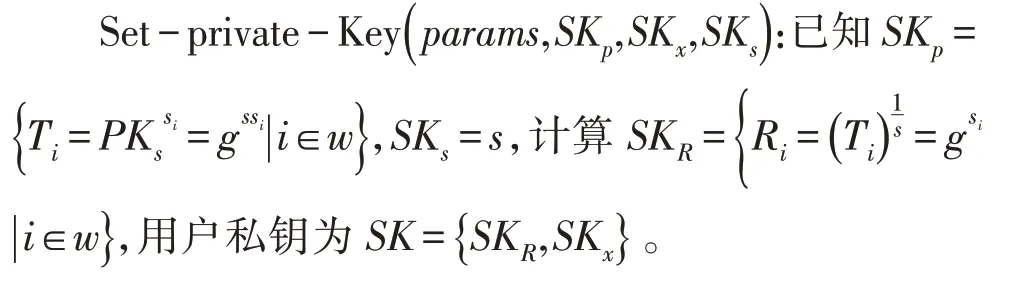
5)签名阶段

6)验证阶段
Verify-Sign(params,T,m,PK,PKx,σ):params为系统参数,树形访问结构为T,消息为m,树形访问结构根结点为τ,验证签名等式如下:
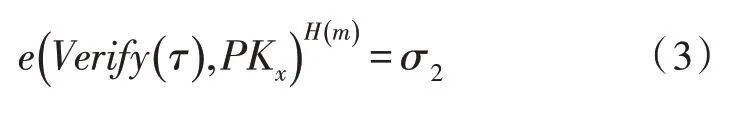
3 安全性分析
3.1 正确性
方案的正确性证明如下。
当Node为树形访问结构根结点τ时,。验证签名:
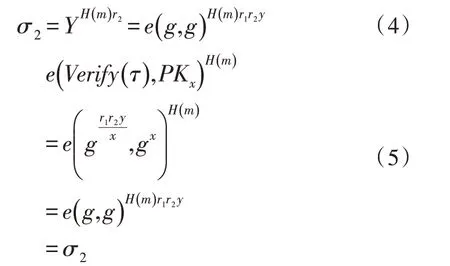
3.2 匿名性
定理1:该方案在选择属性攻击下,满足匿名性。
证明:假设一个多项式时间敌手A模拟签名者。设C为挑战者应答A的询问。模拟交互过程如下:选择两个长度相同的属性集合{w0,w1},C任选其一进行签名,则敌手A正确区分签名及部分私钥的概率可忽略。
1)系统建立阶段:C运行系统生成算法Setup(λ),生成系统参数params,系统主密钥MSK={y} 。
2)密钥值建立阶段:敌手A选取随机数s,x∈,计算PKs=gs,PKx=gx,SKs=s,SKx=x。
3)部分私钥提取阶段:挑战者C随机选择一个比 特b∈{0,1},并执行算法 Extract-partial-private-key (params,wb,MSK,PKs)以生成部分私钥,,其中i∈U,为随机选取的;生成本次签名的系统公钥
4)私钥建立阶段:A运行Set-Private-Key(params,SKpb,SKx,SKs),生成SK={SKR,SKx} 。
5)签名阶段:A运行Sign(params,SK,m),生成,其中
6)验证阶段:C运行Verify-Sign(params,T,m,PK,PKx,σb),给出签名的验证结果。
7)挑战阶段:敌手已知消息{w0,w1}、部分私钥SKPb、签名σb={σ1,σ2} 以及签名的验证结果。但签名过程中仅有部分私钥SKpb含有属性信息,而经过r1及ti的随机化,敌手无法正确区分属性属于哪个集合。
综上所述,敌手A成功输出b∈{0,1} 的概率为,故方案满足匿名性。
3.3 不可伪造性
定理2:在标准模型下,提出的无证书属性基签名方案满足不可伪造性。
证明:不失一般性,假设存在攻击者A1(不知系统主密钥但可以对用户的公钥进行任意的替换)、A2(知道系统的主密钥不能替换目标用户的公钥),定义攻击游戏Game1,Game2,在游戏过程中C为挑战者,模拟挑战询问。
1)Game1:模拟攻击者A1的伪造游戏
系统参数设置:挑战者C执行系统参数生成算法Setup(λ),从而生成系统参数params={g,G1,G2,e,H}及主密钥MSK={y} 。C发送params给攻击者A1。
①询问阶段
秘密值询问:A1对用户i的秘密值进行询问,C运行算法Set-Secret-Value(params)生成SKxi=xi和SKsi=si。如果用户i的部分私钥提取询问已经被执行,则输出⊥,否则将SKxi和SKsi发送给用户A1。
部分私钥提取询问:A1对用户i的部分私钥进行询问,C运行 Extract-Partial-Private-key(params,w,MSK,PKsi)生成部分私钥SKPi=如果已经执行了用户i的秘密值询问,则输出⊥,否则发送SKPi给A1。
签名询问:A1对用户i在消息mj的签名进行询问,C运行算法Sign(params,SKi,mj)输出签名σi={σ1i,σ2i},其中
②伪造阶段
A1询问以上信息后,输出一个签名者i在消息m∗上的有效签名σ∗。签名需满足下面两个保证条件:a.签名者i未同时提交秘密值询问和部分私钥提取询问;b.没有对消息m∗进行过签名询问;
以下分析A1在m∗上的签名σ∗的有效性概率,SK={SKR,SKx} 需A1通过询问获取,生成签名的必要条件。SKx可以由秘密值询问获取,SKR=,SKp需要经过部分私钥提取询问获得,SKs可以通过秘密值询问而获取,SKR及SKx是经过Set-Secret-Value 算法随机生成的,SKp的随机性由Extract-Partial-Private-key 算法的ri和ti保证,由条件a 通过计算SK伪造有效签名的概率可以忽略。在无证书签名询问中,r2保证了询问签名σi的随机性,由条件b 通过询问签名方式获取有效签名的概率可忽略。
因此,Game1 中A1获取胜利的概率可忽略。
2)Game2:模拟攻击者A2的伪造游戏
系统参数设置同Game1,C将params和MSK发送给攻击者A2。
①询问阶段
秘密值询问:同Game1,C将PKxi和PKsi发送给攻击者A2;
部分私钥提取询问:同Game1,A2可获取wi,SKpi;
签名询问:同Game1;
②伪造阶段
A2通过以上询问,输出一个签名者i对消息m∗的有效签名σ∗。
签名满足保证条件:消息m∗未经签名者i的签名询问。
以下分析签名的有效性:因为A2不能执行公钥替换,所以A2输出的签名验证必须为合法用户的公钥,A2已通过秘密值询问获取一系列的用户有效公钥值。由于签名需要相对应的用户私钥才能使伪造的签名验证通过,而,根据公钥要求解私钥xi相当于解离散对数问题,因此,A2伪造成功签名的概率可忽略,从而赢得Game2 游戏的概率可忽略。
综上所述,A1赢得Game1 的概率可忽略,A2赢得Game2 的概率可忽略,所以提出的无证书的属性基签名方案满足不可伪造性。
4 效率分析
表1 给出了提出方案与现有效率较高的树形访问结构属性签名方案在功能上的对比。
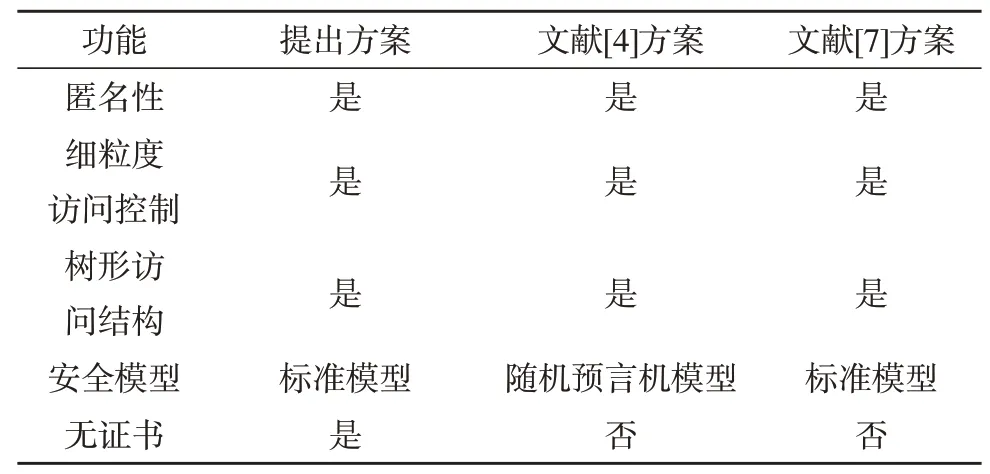
表1 方案功能比较
表2 给出了提出方案与现有方案在性能上的对比。ω表示签名者拥有的属性个数,|G1|表示G1中元素的长度,|G2|表示G2中元素的长度,l表示访问结构中所有属性的个数,m表示消息的长度,S表示访问结构中用到的所有内结点的集合,内结点集合的元素个数表示为ξ=|S|,h表示为访问结构中所有“threshold”中门限的和,P和EXP分别表示双线性对运算和指数运算的时间。
通过表1 和表2 的比较可以看出,提出方案在功能上具有无证书性,可以有效地削弱KGC 的权限,避免密钥托管问题。在性能上,提出方案比其他两个方案具有更短的密钥长度和签名长度,并且在签名生成和验证开销上花费更短的时间。

表2 方案性能比较
实验中树形访问结构如图2 所示,为3 层结构,其中“threshold”的门限值为2,签名者的属性集合ω={1,2,4,5,7}。图3 给出了在Inter(R) Core(TM)2 DuoT6670 CPU 2.2GHz 2.00 GB RAM 的计算机上,提出方案与文献[4]算法的平均运行时间对比,用JPBC 库在Eclipse 上实现。
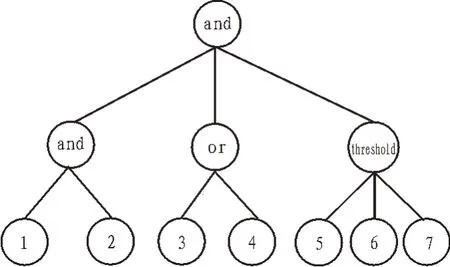
图2 树形访问结构示意图
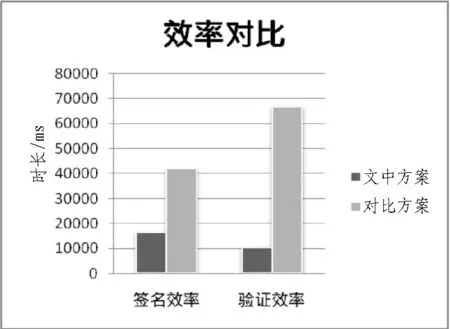
图3 算法的平均运行时间对比
5 结论
提出的方案可用于电子医疗档案系统的用户信息更新的操作方案,使用无证书的属性基签名来保证用户更新信息的完整性。无证书密码体制的使用,削弱了密钥生成中心的权限,解决了传统的密钥托管问题。在系统安全性得到提高的情况下,效率也有了很大的提升。

