分形视角下股票市场的聚类分析

张红梅，王 沁，汪 玲，董 鑫

（西南交通大学数学学院，成都 611756）

一直以来，有效市场假说（EMH）作为金融学的研究基石，是分析金融市场的理论前提.然而，国内外学者［1-4］对金融市场的研究表明，由于受到众多复杂因素的影响，金融市场并不符合有效市场假说，而是表现出非常复杂的非线性特征.多重分形作为一种重要的非线性方法，能解释众多传统有效市场假说无法解释的现实经济现象，因此常常被用来研究金融市场的特征.聚类是数据挖掘和时间序列分析中一类重要的方法，所谓聚类就是将数据划分成多个有意义的簇，使得簇中的数据尽可能相似，而簇与簇之间的数据具有明显的差别.目前，时间序列聚类分析被广泛用于能源系统［5］、自然灾害［6］、公共交通［7］、医学［8］和航天［9］等多个领域.针对金融领域，由于金融时间序列具有高维度和高动态的非线性特点，因此常常结合多重分形来对其进行聚类分析，这有助于分析金融市场的板块效应和联动机制，对制定最优投资组合，降低投资风险有重要的意义.

随着分形理论的不断发展和完善，越来越多的学者使用多重分形消除趋势波动分析法（MF-DFA）［10］和多重分形消除趋势交叉相关分析法（MF-DCCA）［11］来探讨金融市场的动态规律.He和Chen［12］用MF-DFA法研究国际石油市场价格的多重分形特征，结果表明Brent和WTI石油市场均存在多重分形结构；Dewandaru等［13］用MF-DFA法探讨市场的分形特征并制定了有效的投资策略；Yin和Shang［14］利用修正的MF-DCCA法分别研究了美国和中国股票价格的自相关性和交叉相关性，实证结果表明，中美股票市场均存在多重分形特征，且分形强度不同；Cao等［15］用MF-DFA法研究中国股票市场的对称性，实证结果表明上涨趋势下，股票的多重分形强度更强，波动越大不对称性越明显.

近年来，越来越多的学者将分形理论和其他算法结合，常见的是与聚类分析相结合.钟维年等［16］基于分形维和多重分形谱，对上海股票市场进行分类，结果发现同一类型的股票在走势、流通性等方面高度一致，而不同类型的股票存在较大差异；黄超等［17］基于分形理论，使用聚类分析法研究全球证券市场24个主要指数的特征；袁铭［18］基于标度曲线对股票市场的金融时间序列进行聚类，发现该方法能很好地揭示股市的行业聚集性和板块间的关联性；张鑫等［19］将分形和K均值聚类分析结合，应用到轴承故障诊断，发现该方法能很好地识别轴承的故障.

从上述文献可以看到，股市、期货和外汇市场的金融时间序列均存在多重分形特征.本文充分考虑金融时间序列的复杂性特征，从分形的角度来分析股票市场的规律，将广义Hurst指数分布和多重分形谱的两个特殊值作为反应股票波动特征的指标，其中Hurst指数分布选取的指标为均值、标准差、偏度和峰度，多重分形谱的两个指标分别为多重分形谱宽度Δα和反应最大、最小概率分形维差的Δf，并以欧氏距离函数作为测度函数，使用层次聚类法对股票进行归类，深入分析每一类中股票的特征，为构建投资组合提供了合理的建议.与传统多重分形消除趋势波动分析法不同的是，本文在消除序列趋势时，采用的是经验模态分解法（EMD）［20］，该方法能更好地消除序列趋势.

1 研究方法——多重分形指标计算

多重分形消除趋势波动分析法（MF-DFA）是由Kantelhardt［10］提出的，主要用来研究金融时间序列的多重分形特征.其思想大致如下：

1）重排列序列.设x(t)为任意的收益率时间序列，t=1,2,…,N.其中N是时间序列的长度，对收益率序列x(t)进行累计离差和处理，得到重排列序列x(i)，i=1,2,…,N.

式中：

2）等间距分割区间.将累积离差和序列x(i)分割成Ns=[N/s]个不重叠的子区间，每个子区间的长度为s，s的取值范围为10～N/5.由于时间序列的长度N通常不是s的整数倍，为了充分利用序列涵盖的信息，从序列尾部向前反向划分区间，由此可以得到2Ns个区间.

3）EMD法消除趋势.使用经验模态分解法（EMD）分解每一个子区间序列，并提取趋势项x͂m(k)，其中：m=1,2,…,2Ns；k=1,2,…,s.

4）q阶矩波动函数.计算消除趋势后的波动函数：

再由波动函数推导出相应的q阶矩波动函数：

5）多重分形指数（广义Hurst指数）.q矩阶波动函数Fx(q,s)依赖于区间长度s和矩的阶数q，且与多重分形指数存在幂律关系：

利用双对数坐标线性拟合来估计h(q)，h(q)通常称为多重分形指数.若h(q)不随q变化，则为单分形；若h(q)随着q非线性变化，则为多重分形.h(q)>0.5时，序列存在长记忆性特征；h(q)<0.5时，序列存在反持续性特征.

6）多重分形谱.若收益率序列x(t)存在多重分形特征，则用多重分形谱分析法［21］，求得其质量指数t(q)：

相应的奇异标度指数α和重分形谱f(α)为：

奇异标度指数α用来刻画序列局部的分形特征，在多重分形谱中，常常关注两个特殊值Δα=αmax-αmin和Δf=f(αmin)-f(αmax)，Δα称为多重分形谱宽度，Δα越大表示分形越显著；参数Δf用来表征最大、最小概率分形维差，若Δf>0，说明股票有更大的概率在高收益波动；若Δf<0，说明股票有更大的概率在低收益波动.

2 实证分析

2.1 数据收集与分析

行业分析是股市基本面分析的重要内容，行业股票的分类便于对股票进行分析研究.目前，行业板块已逐渐成为投资选股的重要依据，因此本文从不同行业板块中选取股票来研究股票市场的特征.把能源、酿酒、家用电器和房地产4个板块作为研究对象，分别从每个板块中随机选取5只股票，获取股票的日收盘价，数据来源于“通达信”客户端，具体时间窗为2010年1月4日至2020年3月19日，由于各种原因使股票停牌，导致在时间窗内每只股票的样本容量不同，具体样本及其容量如表1.

表1 股票名称与样本容量Tab.1 Stock names and sample sizes

在获得日收盘价后，根据公式rt=lnpt-lnpt-1计算股票日对数收益率，使用日对数收益率分析股票波动的特征，由于篇幅有限，表2只给出了部分股票的描述性统计和正态性检验结果.由表2可以看出，4只股票收益率序列的偏度都小于0，样本均值几乎为0，峰度都大于0，整体呈现出“尖峰厚尾”的特征，从K-S检验结果也可以看到，股票收益率序列均不服从正态分布.同样的，剩下的16只股票也具有相同的特征，说明所选股票收益率序列不符合有效市场假说，而是呈现出复杂的非线性特征.

2.2 多重分形特征分析

使用重复划分区间的MF-DFA法，检验股票收益率序列多重分形特征的存在性.区间长度s的取值范围为30～100，波动函数的阶数q在-10到10之间变化.同样，由于篇幅的限制，图1只给出了部分股票收益率序列的广义Hurst指数图和多重分形谱图.

图1 收益率序列的广义Hurst指数图和多重分形谱图Fig.1 Generalized Hurst index diagram and multifractal spectrum diagram of the return series

从Hurst指数图（图1a）可以看到，4只股票收益率序列的广义Hurst指数均随着q值呈非线性变化，说明股票收益率序列均存在多重分形特征；4只股票收益率序列的Hurst指数变化趋势相似，均随着q值的增大而减小，且在q=0时出现拐点.建投能源、泸州老窖、格力电器的Hurst指数十分接近，尤其是q值接近0时，说明这3只股票收益率序列的多重分形强度接近；绿地控股的Hurst指数整体比其他3只的大，说明绿地控股的多重分形强度更强，其股票收益波动也更剧烈，与另外3只股票存在较大差异，说明用Hurst指数分布聚类是合理的.

从多重分形谱图（图1 b）可以看到，序列的多重分形谱既存在差异性也存在相似性.相似性主要体现在多重分形谱的走势上，均呈“倒钩”形，差异性主要体现在“倒钩”形的形态和多重分形谱的宽度上，建投能源、泸州老窖、格力电器的多重分形谱呈“左偏”状态，而绿地控股的多重分形谱呈“右偏”状态，绿地控股的多重分形谱宽度明显宽于其他股票，这也说明使用多重分形谱进行聚类是合理的.用同样的方法分析其他未展示的16只股票可以得到类似的结论.

2.3 聚类结果和比较

广义Hurst指数仅能从整体上刻画序列的波动特征，而多重分形谱的两个特殊值Δα和Δf能刻画序列波动的均匀性和波动幅度的相似性，因此将广义Hurst指数分布和多重分形谱的两个特殊值作为衡量金融时间序列相似性的指标.其中广义Hurst指数分布的指标是广义Hurst指数的均值、标准差、偏度和峰度，多重分形谱的指标为Δα和Δf.将传统欧式距离函数作为测度函数，使用层次聚类法对股票序列进行分类，当目标分为3个类别时，聚类结果如表3所示.

表3 股票聚类结果Tab.3 Stock clustering results

根据表3的聚类结果，分析每一类股票的波动特征.使用R软件对每一类股票的广义Hurst指数进行描述性统计分析，表4给出了相应的结果.

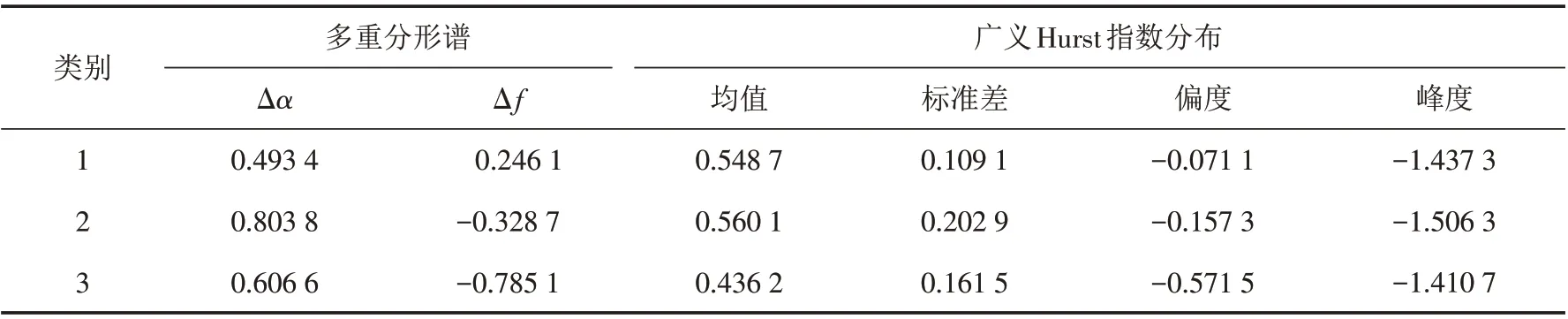
表4 股票波动分析结果Tab.4 Results of stock fluctuation analysis

分析表4，可得到如下结果：

1）观察目标分类1的多重分形谱和广义Hurst指数分布，从表中可以看出，该类中广义Hurst指数的标准差、偏度的绝对值均是最小的，表明该类的广义Hurst指数集中在均值附近波动，整体的波动幅度较小；从Δα值也可以看到，类别1的多重分形谱宽度是最小的，说明该类别中股票序列的多重分形强度最弱，股票价格的波动最稳定.再看广义Hurst指数均值和Δf值，Hurst指数均值为0.548 7，大于0.5，说明该类别中的股票存在长记忆性特征；Δf值大于0，说明该类别中股票有较大的概率在高收益波动.由于长记忆性的存在，使得这种趋势会持续一段时间，股票在未来一段时间内仍然会在高收益波动，因此，将此类股票称为“绩优股”.

2）观察目标分类2，该类别中广义Hurst指数的标准差和峰度的绝对值都是最大的，偏度的绝对值居中，广义Hurst指数波动较大.从Δα值也可以看到，此类的多重分形谱宽度最大，说明该类别中股票序列的多重分形强度最强，股票价格的波动最剧烈.再看Hurst指数均值和Δf，Hurst指数均值大于0.5，说明该类别的股票存在长记忆性特征；Δf值小于0，股票序列有更大的概率在低收益波动.由于长记忆性的存在，在未来的一段时间内，股票将持续在低收益波动，因此，将此类股票称为“垃圾股”.

3）分析目标分类3的特征，观察广义Hurst指数的分布，可以看出，广义Hurst指数的标准差处于居中位置，峰度的绝对值最小，偏度小于0且绝对值最大，表明Hurst指数大部分位于均值左边，且有更大的概率处在小波动；多重分形谱的宽度Δα居中，说明该类别中股票序列的多重分形强度居中.再观察广义Hurst指数均值和Δf，可以看到Hurst指数均值小于0.5，表明该类股票存在反持续性的特征；Δf值小于0，说明股票有更高的概率在低收益波动.由于反持续性特征的存在，股票收益有回升的趋势，因此，将该类别的股票称为“潜力股”.

3 结论

本文以4个行业板块的股票日收益率数据为基础，使用重复划分区间下的MF-DFA法，分析了股票的多重分形特征，并基于广义Hurst指数分布和多重分形谱的两个特殊值，使用层次聚类法比较行业板块股票间的多重分形特征，得到如下结论：

1）多重分形指数分析结果表明，本文所选股票均存在多重分形结构，且每只股票的多重分形强度不同.

2）从聚类分析结果来看，将股票市场分为绩优股、垃圾股、潜力股3类比较合理.

3）研究结果能为构建投资组合提供合理的建议.当投资者在投资股票时，可以从绩优股和潜力股中选取股票来构建投资组合，从而有效地降低投资风险，并且实现收益最大化.