阿波罗尼斯圆的一个几何结论及应用

江西省瑞金第一中学(342500)魏东升

古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下著名结果:

到平面上两定点距离比等于已知数的动点轨迹为直线或圆.

此结果中的圆就是著名的阿波罗尼斯圆,简称阿氏圆.有关阿波罗尼斯圆的文章很多,但涉及其应用的文章大多基于代数视角,本文探究阿波罗尼斯圆的一个几何结论及其在解题中的妙用:

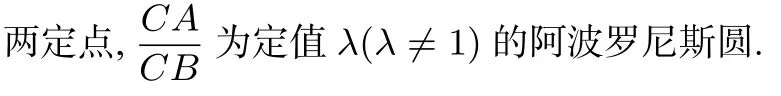
1 解三角形

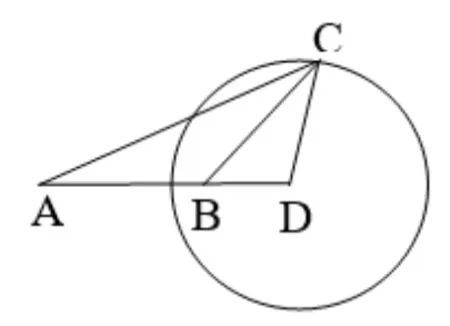
图2

变式1ΔABC中,角C的平分线交AB于T,且AT=2,TB=1,若ΔABC中AB边上的高长为2,则ΔABC的周长为____.

图3

2 立体几何

例2在棱长为6 的正方体ABCD−A1B1C1D1中,E是BC的中点,F是正方形DCC1D1内的动点,且满足∠AFD=∠EFC,则三棱锥F−BCD的体积的最大值为____.

图4

变式2在直四棱柱ABCD−A1B1C1D1中,底面ABCD为菱形,E,F分别是BB1,DD1的中点,G是AF的中点,FG=3,则ΔAEF的面积的最大值为____.

图5

3 平面向量

例3已知向量a,b满足|b|=3,|a|=2|b−a|,若|a−2b|≤n2−3n,求n的取值范围.

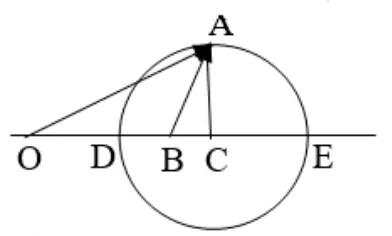
图6

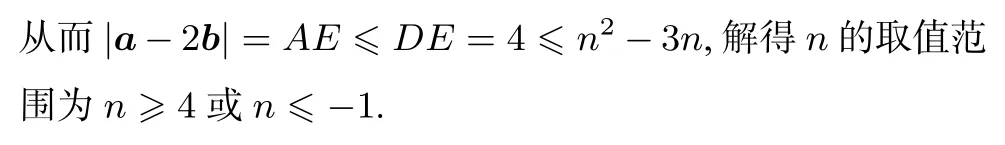
变式3已知a,b,c是平面内三个单位向量,a·b=0,求|a+2c|+|2a+b−c|的最小值.

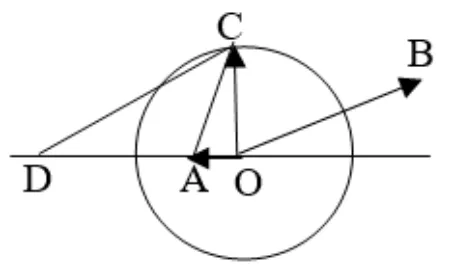
图7

评析向量是数与形的完美结合在上述例子中可谓体现地淋漓尽致,灵活运用其几何意义往往有事半功倍地效果,其中变式3 是借助阿波罗尼斯圆结论解题的典型的“胡不归”问题.

4 解析几何

例4(2013年高考江苏卷)如图8,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x−4,设圆C的半径为1,圆心在l上.

图8

(1)略;(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.

解析(2)因为圆C的圆心在在直线l:y=2x−4上,所以设圆心C为(a,2a−4),则圆C的方程为:(x−a)2+[y−(2a−4)]2=1.又因为MA=2MO,可知点M的轨迹是一个阿波罗尼斯圆,如图9,设圆心为D(m,n),根据结论可知

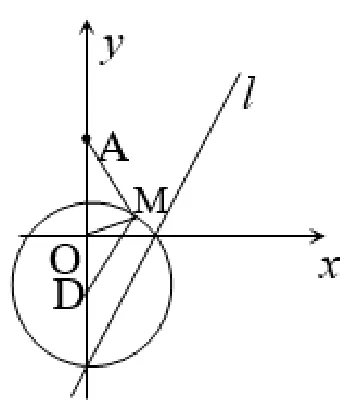
图9

变式4(2015年高考湖北卷理科)如图10,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2

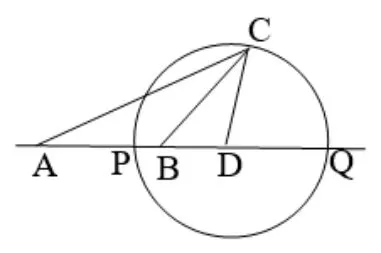
图1

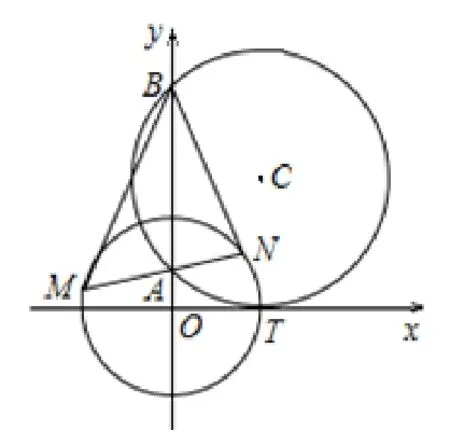
图10

(1)圆C的标准方程为

(2)过点A任作一条直线与圆O:x2+y2=1 相交于M,N两点,下列三个结论:

其中正确结论的序号是____.(写出所有正确结论的序号)

评析例4 通过假设点M的坐标进行代数运算得到圆D的方程也不难,但变式4 如不知道阿波罗尼斯圆的上述结论要想得到正确答案就要下一些功夫了,所以在解析几何问题中多掌握一些相关结论就显得很有必要.

结语本文主要探究了阿波罗尼斯圆中的一个几何结论在不同的数学知识板块中的应用,给我们解决与此有关的问题带来了极大的方便,同时也让我们感受到了数学传统文化的博大精深.作为数学教育工作者,像这样在解决数学问题中向学生渗透数学文化知识,很有必要,也十分有效.