具有输入时延的离散时间多智能体系统事件触发编队控制研究
朱 伟,王治健,曹文吉
(重庆邮电大学 复杂系统智能分析与决策重庆市高校重点实验室,重庆 400065)
0 引 言
多智能体系统作为群体智能领域的一类典型系统,近10余年来受到了广大科研工作者的高度重视,其协同控制在包括航空航天在内的众多领域中展现出了强大的应用潜力。柴院士[1]指出:多智能体协同控制系统是实现运载工具未来需求的自动化系统愿景功能的三大系统之一。
编队控制是多智能体系统协同控制的热点研究问题之一,其通过智能体之间形成的网络进行局部信息传输,调整智能体之间的相对位置,使智能体系统形成与保持特定的编队队形。近年来,学者们针对不同类型的多智能体系统开展编队控制问题的研究,如一阶系统[2],二阶系统[3],一般线性系统[4-5]以及哈密顿系统[6]等。
最近,林志贇教授团队将复Laplacian引入到多智能体系统编队控制研究中[7-9],基于相对位置信息,得出连续线性分布式控制策略,证明了稳定增益矩阵的存在性,得出了编队形成的几何条件,即图是双根的,从而实现了多智能体系统的完全分布式编队控制。然而,留意到关于多智能体系统编队控制的大部分研究成果中,控制器需要使用邻居的连续信息,导致编队的实现需要消耗大量的通信资源、在线计算信息等,对编队的实际应用具有巨大的挑战性。基于事件触发的通信机制提供了一种能有效节约多智能体系统资源的新方法,由于其在减少信息交换方面的潜在优势,受到了广泛关注。文献[10]研究了基于实Laplacian的二阶多智能体系统环形编队的问题,证明了在集中式和分散式的事件触发控制协议下,二阶多智能体系统能形成环形编队。文献[11]研究了基于事件触发机制的环形编队问题,假设所有智能体均在同一圆环上移动,每个智能体仅能获取自身与其前后2个相邻智能体的相对位置信息。文献[10-11]的研究局限在环形编队。文献[12]研究了连续和离散系统在事件触发控制下基于复矩阵的编队问题,在满足图论的条件下,系统能形成具有3个自由度——平移、旋转、收缩的相似编队且不存在Zeno现象。文献[13]研究了存在输入时延的连续多智能体系统在事件触发控制下基于复矩阵的编队问题,给出系统能形成相似编队的充分条件,且排除了Zeno现象。
本文将针对一类由复差分方程描述的多智能体系统的编队问题开展研究。利用智能体的状态信息及指数衰减函数构造了事件触发函数,进而根据事件触发条件确定事件触发序列,并在考虑智能体控制器存在输入时延的情况下,设计了一类基于事件触发机制的控制器,从而获得了多智能体系统形成任意给定编队的充分条件,并给出了输入时延的存在范围。进一步,排除了事件触发序列在离散意义下可能存在的Zeno现象。最后通过数值仿真例子验证了本文理论结果的有效性。
1 基本定义及模型
为了刻画智能体之间的连接关系,引入如下的图论知识。
无向图G=(ν,ε,A) 表示智能体之间的通信拓扑图,其中,ν={v1,…,vn}为顶点集合;ε⊆ν×ν为边集;A=(aij)n×n为邻接矩阵,aii=0,aij=aji>0 如果(i,j)∈ε,否则aij=0。Ni表示智能体i的集合,即Ni={j:(i,j)∈ε)}。
复LaplacianL的元素L(i,j)由(1)式确定
(1)
(1)式中,ωij满足
(2)
(2)式中,ξ=[ξ1,ξ2,…,ξn]T∈n,ξi≠ξj当i≠j, 为任意编队。
定义1[8]如果ker(L)=c11n+c2ξ,则称由Lξ=0指定的框架图(G,ξ)是相似的,其中,c1,c2∈。
定义2[8]对顶点v及非孤立点集u⊆G,若去掉任意不同于v的顶点后,还存在一条u中的顶点到顶点v的路,则称顶点v是2可达的。
定义3[8]如果无向图G中存在2个顶点,使得其他顶点到这2个顶点都是2可达的,则称无向图G是双根的,这2个顶点称为图G对应的根。
考虑复平面中的n个智能体,其动力学方程为
zi(t+h)=zi(t)+hui(t),i=1,2,…,n
(3)
(3)式中,zi∈与ui(t)∈分别表示第i个智能体的状态与控制输入。本文在假设系统状态可测的基础上研究控制器存在输入时延时,系统(1)的基于事件触发机制的任意队形编队问题,为此控制器设计如下
(4)
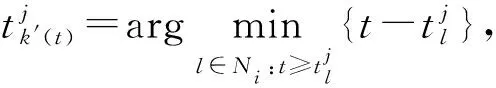
(5)


ei(t-τ)-ej(t-τ))
(6)
令Q为(n-2)×n的行正交矩阵,即QQT=In-2,且Q1n=0,Qξ=0。由文献[9]知,多智能体系统(3)能形成目标编队ξ等价于y:=Qz→0,z=[z1,z2,…,zn]T。
注意到In-QTQ为向量1n与ξ生成空间上的正交投影矩阵,且1n与ξ在L的零空间中,所以L(I-QTQ)=0 ,即L=LQTQ。
故,由(3)式和(6)式得
y(t+h)=y(t)-hρQΓLQTy(t-τ)-
hρQΓLe(t-τ)
(7)
(7)式中:y(t)=[y1(t),…,yn(t)]T,Γ=diag{γ1,…,γn};e(t)=[e1(t),…,en(t)]T,
定义4如果对任意初始值zi(0),都存在正常数χ>0与0<ζ<1,使得
‖Qz(t)‖=‖y(t)‖≤χζt,t≥0
(8)
则称多智能体系统(3)能全局指数收敛到任意队形ξ的相似编队。

2 主要结果
引理1[9]给定双根图G及队形ξ,对满足条件Lξ=0的LaplacianL,存在矩阵Γ使得ΓL除2个0以外的特征值可以分布在复平面任意位置。
引理2[12]矩阵QΓLQT与矩阵ΓL具有相同的非零特征值。

引理4若σ(In-2-hρQΓLQT)<1,则存在正常数ψ>0与ζ∈(0,1)使得
‖In-2-hρQΓLQT‖p≤ψζp,
p=0,1,2,…
(9)


证由方程(7),通过简单迭代可知
y(t)=(In-2-hρQΓLQT)py(0)-y(sh))-
p-s-1hρQΓLe(sh-τ)
(10)
进而由引理4有
(11)
由事件触发条件知
(12)
下面将证明对任意N>1有
‖y(t)‖ (13) 若(13)不成立,则必然存在t*=p*h>0 使得 ‖y(t*)‖≥NZηt* (14) 且 ‖y(t)‖ (15) 所以,由(11)—(15)式得 NZηt*≤y(t*)≤ ψζp*‖y(0)‖+hρ‖QΓLQT‖ ψζp*‖y(0)‖+ Nψζp*‖y(0)‖+ (16) 情形1Z=Z1 此时有ψ‖y(0)‖-Z1≤0,则 情形2Z=ψ‖y(0)‖ 此时有ψ‖y(0)‖≥Z1,则 NZηt* NZηt*矛盾。 以上2种情形矛盾显示,(3)式对任意N>1均成立,令N→1即可得 ‖y(t)‖≤Zηt,t≥0 (17) 因此,z(t)全局指数收敛到c11n+c2ξ,即多智能体系统(3)能全局指数收敛到任意队形ξ的相似编队。 因为z(t)全局指数收敛到c11n+c2ξ,所以存在正常数T>0使得 ‖zi(t)-(c1+c2ξi)‖≤Zηt,t>T (18) ‖zi(t)-(c1+c2ξi)‖≤ (19) 由事件触发时间的确定知,只有当fi(t)≥0 时事件才会被触发,即 (20) 因此,由(19)式和(20)式可得 即 (21) 本部分将利用包含6个智能体的多智能体系统进行数值仿真,验证本文所得理论结果的有效性。假设 ξ=[-1+ι,-2+2ι,-2-2ι, 2-2ι,2+2ι,1+ι]T, 智能体之间的通信拓扑如图1。 图1 通信拓扑图Fig.1 Communication graph 并假设智能体之间有连接,则权重为1,否则为零。显然节点1与2为此图的2个根。由ξ可知,Laplacian矩阵可以选择如下 (22) 满足rank(L)=n-2,Lξ=0。 简单计算可知,Laplacian矩阵L的特征值为 λ1=-5.9767-0.9778ι;λ2=-1.8096+0.5166ι;λ3=-1.8425-2.3150ι;λ4=-0.3713-2.2239ι;λ5=0,λ6=0。令Γ=diag{-1,-1,-1,-1,-1,-1}, (23) 则QΓLQT的特征值为λ1=5.976 7+0.977 8ι,λ2=1.809 6-0.516 6ι,λ3=0.371 3+2.223 9ι,λ4=1.842 5+2.315 0ι。因此,根据定理1,可以选择α,γ,β1,β2,τ使得多智能体系统队形ξ的相似编队。 令z(0)={1+ι,2-ι,3+1ι,4-1ι,5+ι,2-ι}T,h=0.000 1,ψ=1,η=0.36,ζ=0.35,δ1=0.01,δ2=2.2,ρ=1,α=0.37,β1=0.01,β2=2.2,γ=0.35,τ=0.000 1。仿真结果如图2,图3,可见相似编队达到且事件触发时间序列不存在Zeno现象。 图3 事件触发时间序列Fig.3 Event-triggered timesequences 针对存在输入时延情况下的多智能体系统编队问题,本文利用图论、矩阵理论和稳定性理论研究了事件驱动控制下一类由复差分方程描述的多智能体系统的编队问题,设计了含输入时延的事件驱动控制器,其驱动时间序列由构造的事件触发函数确定。利用事件触发控制器,很大程度的减少了控制器的更新次数,并得到了系统形成任意给定编队的充分条件也排除了离散意义下的Zeno现象。数值仿真结果验证了理论的有效性。
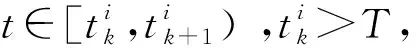

3 数值仿真



4 结 论

