低时间复杂度的极化码译码算法

陈发堂，赵昊明，石 丹，陈 洋

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

极化码设计的核心理论是对信道的极化方案，信道极化过程主要包括2部分：信道联合过程和信道分裂过程。通过信道联合和信道分裂，各个子信道的二进制对称容量将呈现两极分化形式。随着信道联合数的增加，一部分信道的容量趋近于1；另一部分则趋近于0。正是利用这种极化现象，我们用趋近于1的信道传送信息，而趋近于0为冻结位，一般为0[1]。理论推导证明，随着码长N趋于无穷大，极化码是一种可以达到香农信道容量的理想码字。

串行消除(successive cancellation，SC)译码是最早提出的极化码译码方法[1]，它可以被看做是一种树的遍历。在SC译码中，以深度优先的方式访问码树的节点，因此，采用这种方式会有较大的时间复杂度。所以对不必要的子树进行修剪是提高SC译码性能的关键，在文献[2-4]中对SC译码做了优化，在满足特定条件时可以停止子树的遍历，从而降低时间复杂度。

极化码串行抵消列表译码(successive cancellation list，SCL)[5]是目前极化码应用最广泛的译码器。可以认为SCL是L个并行SC译码器，尤其是极化码在加了冗余循环校验(cyclic redundancy check，CRC)之后[6]，大幅度地提高了SCL译码器的纠错性能，但是复杂度和时延很高。球形译码(sphere decoding, SD)找到传输数据的ML(maximum-likelihood)估计，但是球形译码的时间复杂度是可变的，并且译码延迟是不可预期的。SD译码过度依靠半径的选择，半径过大，候选路径过多算法复杂过大。半径过小，SD无法找到ML估计。为了克服这些问题，提出了列表球形译码[7](list sphere decoding，LSD)。

本文改进了文献[10]中的一种剪枝算法并与文献[9]中的联合译码算法相结合，提出了SC-SCSL(syndrome check-successive cancellation sphere list)译码，相比于CA-SCL译码在几乎不损失性能的情况下，时间复杂度降低了50%以上。

1 极化码简介

Arikan所提出的信道极化理论被认为是编码理论中的一个重大突破。因为它是经过严格证明，具有能力实现香农信道容量和低复杂度的编码和解码算法[1]。

1.1 极化码编码

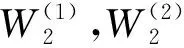
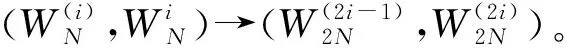
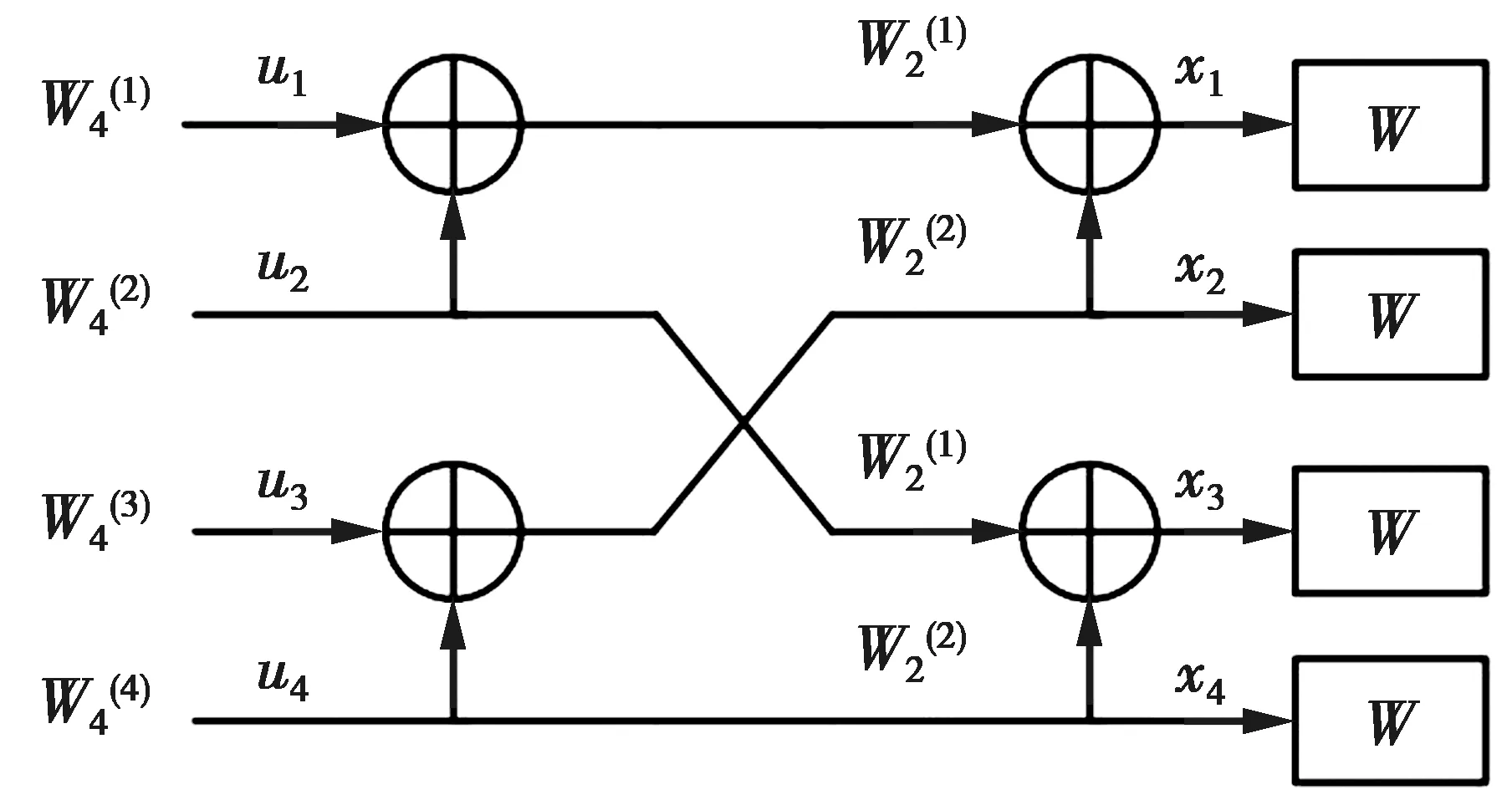
图1 长度为4的极化码编码Fig.1 Polar code of length 4

1.2 SC译码

SC译码算法可以解释为对二进制树的遍历，如图2，子节点通过接收母节点的软信息图中的α，经过计算似然比(logarith-mic likelihood ratios,LLR)，硬判决后传回β。树是通过深度优先搜索且左边的优先级高。

图2 SC译码树Fig.2 SC decoding tree

(1)

(2)

(1)—(2)式中:

f(a,b)≈sign(a)sign(b)min(|a|,|b|)，

g(β,a,b)=(-1)βa+b

(3)

对于子节点β，通过硬判决得到

(4)

(5)

保留的L条路径，其中最小PM值对应的路径为译码结果。但SCL译码的复杂度很高，文献[8]所提出的综合检测串行消除(syndrome check successive cancellation，SCSC)译码极大地提高了SC译码的性能。对于非叶子节点若满足了综合检测

(6)

(6)式中：β为Nv位硬判决值得到的矩阵；H为奇偶校验矩阵，可由生成矩阵得到。

该节点下的叶子节点译码结果可直接得到

(7)

(7)式中：u为Nv位译码结果；GNv为行数与列数为Nv位的方阵生成矩阵。

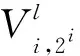
(8)

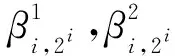
(9)

将会与文献[10]中的结果相矛盾。

1.3 LSD译码

利用GN的下三角结构，SD译码从uN-1开始，并行分裂路径0和1[11]。计算出根节点到子节点的欧氏距离，作为下一比特估计球的半径。所有在球内的候选路径被用于下个比特的估计，重复此过程，直到找出欧式距离最小的候选比特。路径度量值的近似表达式为

(10)

球形译码可以找到传输数据的ML估计，但复杂度不可预期。为了克服这个问题，提出了LSD[12]译码。LSD译码有固定时间复杂度。每次都有一个新比特被估计，它可能的值0和1都需要被考虑。由于存在L组码字候选，所以每次更新的后产生2L组候选路径，其中一半丢弃，没有涉及半径。

2 SC-SCSL译码

首先对ESSCL译码进行了改进，提出了SC-SCL译码；并联合了LSD译码，提出SC-SCSL译码，极大地减少了时间复杂度。

2.1 SC-SCL译码

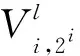
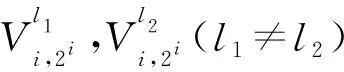
2.2 SC-SCSL译码

SC-SCSL译码：结合上文所述，将长度为N的码字{u1,u2,…,uN}分成2段进行译码。其中,{u1,u2,…,uM}使用SC-SCL(L=LS)译码,而{uM+1,uM+2,…,uN}使用LSD(L=LD)译码，两者并行进行。对结果的LS条路径和LD进行组合，选出通过CRC校验的码字为最终译码结果。如图3，由于译码并行进行，SC-SCSL译码所需的时间为

图3 SC-SCSL译码Fig.3 SC-SCSL decoding

t=MAX(tSC-SCL,tLSD)

(11)

由于引入了CRC，结果可能出现同时满足检测的情况；对此，通过LLR作为可靠性的度量方式，选择LLR最小的为最终结果。

2.3 仿真结果分析

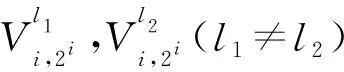
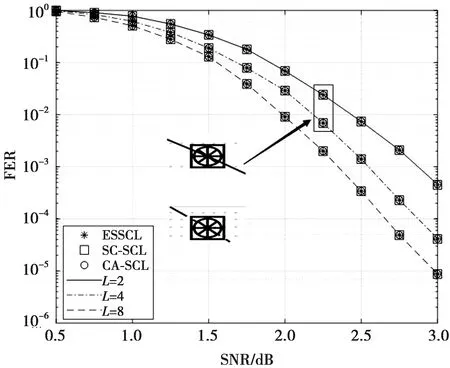
图4 未出现同时满足综合检测时的误帧率比较Fig.4 Comparison of FER when syndrome check is not met at the same time

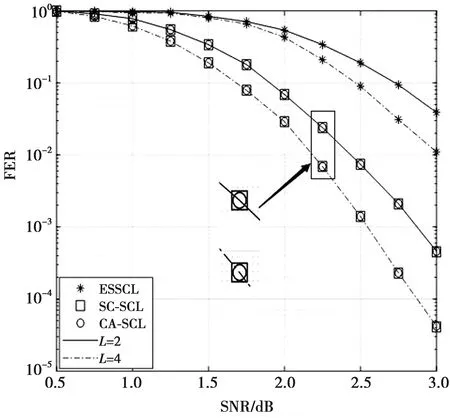
图5 出现相同点同时满足综合检测时的误帧率比较Fig.5 Comparisons of FER when the same points are met with syndrome check at the same time

对(1 024,512)型极化码运用SC-SCSL的FER性能仿真，如图6。其中，SCL,CA-SCL,LSD的搜索路径数相同L=4；SC-SCSL的SC-SCL部分LS=4，LSD部分LD=4，M取683，并且设定CRC校验码类型为CRC-24。

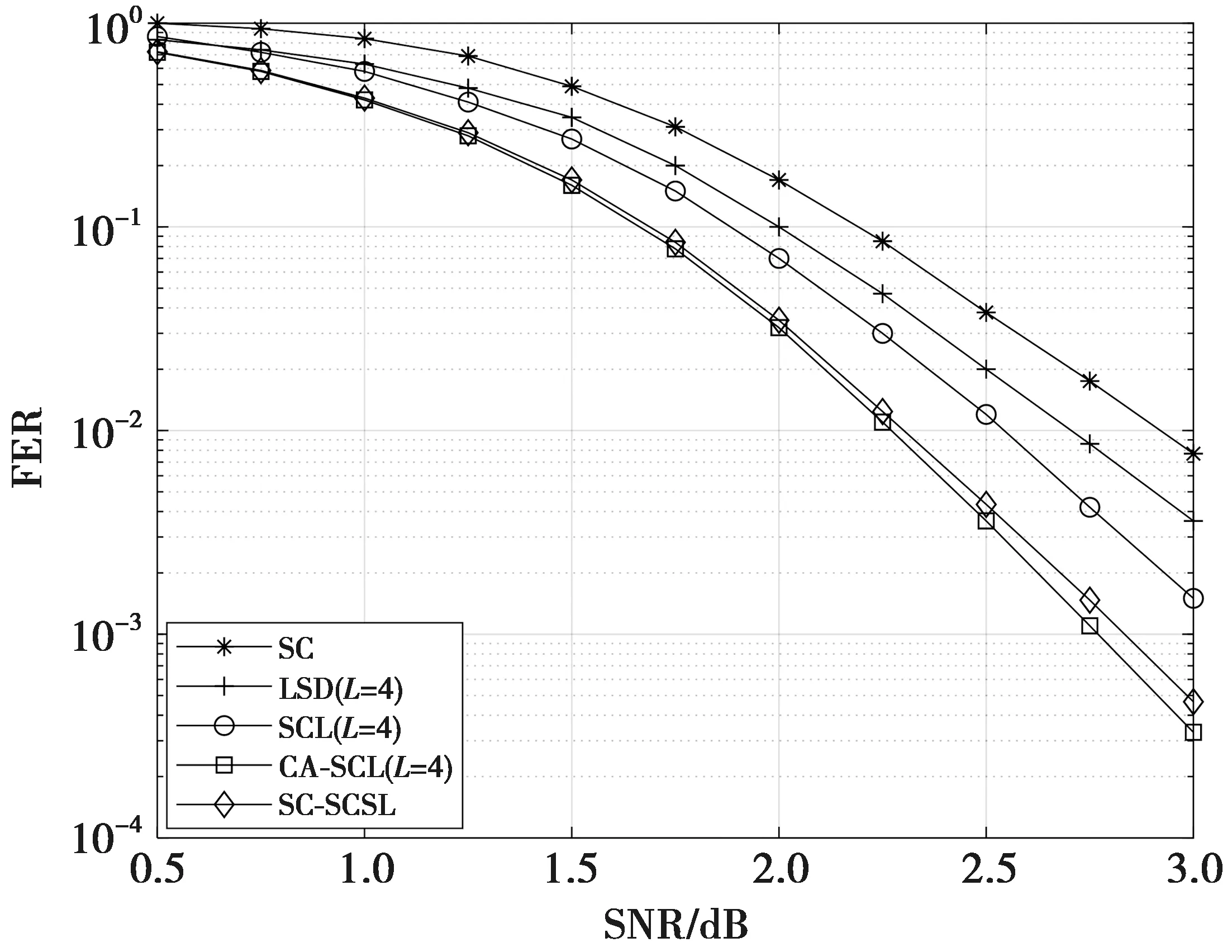
图6 码长1 024的几种算法误帧率比较Fig.6 Comparison of frame error rates of several algorithms with code length 1 024

从图6可以看出，在相同情况下，SC-SCSL的性能明显优于SC，SCL和LSD。虽然相比于CA-SCL在高信噪比时，有一定的性能损失，如在信噪比为2 dB时，有约0.4 dB的性能损失，但由于此算法的并行特性，可极大地降低译码时间复杂度。

3 复杂度分析

作为复杂度的度量标准，本节分别给出了SCL，SC-SCL，LSD的加法次数，乘法次数，和比较次数计算公式。将所提出的SC-SCSL与CA-SCL运算次数进行比较。结果表明，在几乎不损失性能的情况下，时间复杂度降低了50%～55%。

3.1 SCL译码复杂度

(12)

(12)式中：K，Ng，Nf，SASCL，SMSCL，SCSCL分别表示冒泡序列排序时的信息比特数；(3)式中g,f算法的运算次数、加法次数、乘法次数和比较次数。

3.2 SC-SCL译码复杂度

(13)

3.3 LSD译码复杂度

(14)

(14)式中：A是信息比特集合；AC是冻结比特集合；ki为第i个访问比特位置。

3.4 SC-SCSL复杂度比较

由(11)式，SC-SCSL的时间复杂度为LSD和SC-SCL的最大值。表1给出了(512,256)的极化码在LS=LD=4,M=342时，分进行CA-SCL，SC-SCSL,LSD译码仿真时，通过计数器累计的所需加法次数，乘法次数，比较次数。虽然SC-SCSL加入了CRC会在高信噪比时，有轻微的性能损失，但却降低了50%～55%的时间复杂度。仿真结果表明，M=2N/3左右时，SC-SCSL性能最佳。

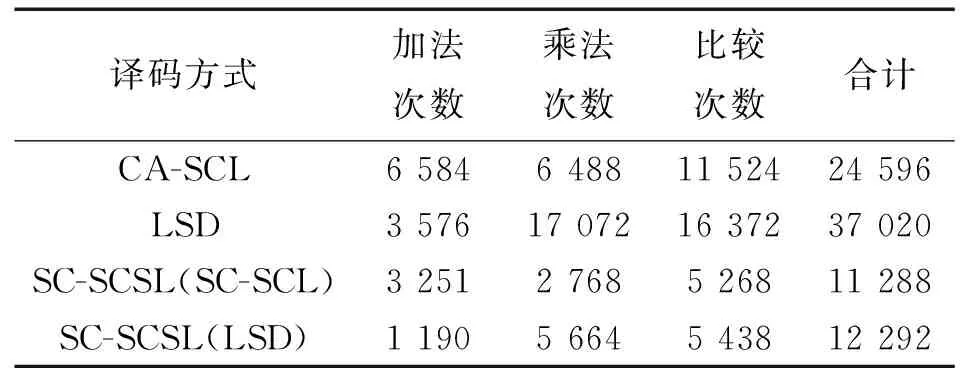
表1 码长512时几种译码算法运算器次数Tab.1 Number of decode algorithm operators for code length 512

4 结束语

为了避免在长码字时同时满足综合检测，采用ESSCL译码导致的错误译码结果，本文提出了一种SC-SCL算法。仿真结果表明，在出现同时满足综合检测时，SC-SCL性能明显优于ESSCL。并联合了LSD译码，提出的SC-SCSL译码在高信噪比时，会有较低的性能损失，但采用并行的方式降低了50%～55%的时间复杂度。接下来将研究LSD译码的剪枝算法，进一步减少复杂度。