稀疏数据下基于用户偏好的协同过滤算法

赵文涛，张 烁

(河南理工大学 计算机科学与技术学院，河南 焦作 454150)

0 引 言

协同过滤推荐技术[1]在推荐系统中占据着很重要的地位。协同过滤推荐技术可以通过用户对物品的评分或者别的行为模式为用户提供优质的推荐服务。基于邻域的算法[2]是协同过滤推荐算法中最基本也是最常用的方法之一。其基于用户对项目的评级，把具有相似评级的用户称为最近邻居[3]，如果找到邻近的邻居，则通过邻居预测用户的未评级项目，然后向用户推荐具有高预测评级的项目。

但是，现存的基于协同过滤推荐算法的推荐系统仍然存在诸多问题，譬如冷启动[4]，数据稀疏性以及可扩展性[5-8]等。一般而言，传统相似性算法可以很好地反映2个用户或项目之间的相似程度，但却没有重复考虑用户偏好。同时，当数据稀疏的时候，用户或项目之间可能没有共同评级项目，相似性计算将无法进行[9]，这也被称为共同评定问题。

1 相关工作

当前，研究人员为协同过滤提供了非常丰富的理论依据和技术支持，文献[10]给出了Jaccard和均方差组合的方法(Jaccard mean squared difference，JMSD)，JMSD中Jaccard用于捕获共同评定项目的比例，均方差(mean squared difference，MSD)用于获取评级信息，该方法解决了传统算法过于依赖距离和矢量导致相似性度量不准确的问题，文献[11]提出了另一种相似性方法，结合6种相似性度量来获得全局相似性，每个测量的权重是通过神经网络学习获得的。但是，这些措施在稀疏数据的情况下不起作用。文献[12]通过考虑用户在不同评级等级上提供的本地和全局评级信息，结合Matusita系数提出一个新的Matusita协同过滤模型 (Matusita collaborative filtering，MCF)，有效解决了稀疏数据集下的共同评级问题，然而该算法只单纯计算用户得分偏好而忽视了用户兴趣偏好，在极端情况下推荐会非常不稳定。文献[13]考虑到传统的余弦相似度不考虑用户偏好的问题，通过用户项目评级值减去项目平均值的方法得到修正余弦。文献[14]提出了一种新的相似性度量，称为新启发式相似性方法，为每个共同评定的项目计算3个参数，分别是接近度，重要性和奇异性，之后，将每个计算出的参数乘以修改后的Jaccard相似度。

上述研究并没有从全局的角度分析用户的兴趣偏好问题，尤其是在数据稀疏的情况下，传统的推荐算法仅使用户间的共同项目，会让推荐的精度更加不准确。针对这些问题，本文通过深入挖掘和分析用户的兴趣偏好，从多角度考虑影响用户偏好的因素；同时，采用全局项目扩大了相似用户的查找范围，避免数据稀疏性引起的相似度计算问题；最后，结合加权的JMSD提高算法的精确度。

2 基于用户偏好的改进协同过滤算法

2.1 稀疏数据下用户的偏好问题

传统用户项目评分矩阵如表1，用户评分是1—5，0表示用户间没有共同项目，如果对用户U1进行推荐，会发现U2,U3与U1并没有共同评分项目，传统相似度计算无法进行，相似度默认为0，U4与U1的有共同项目评分分别为(5,4)和(1,1),根据计算相似度为负值，此时，推荐系统会把优先级高的U2,U3推荐给U1。反观U3对项目的打分非常低，U1却对此类物品有高的评分，从用户偏好的角度出发，U3和U1对物品的喜好有所不同，U2会更适合向U1推荐。但传统的相似性度量显然没有考虑到这个问题，并且现实中的数据往往比较稀疏，用户间的共同项目缺失严重，上述问题出现频率会更多，这会对推荐的精度产生很大影响。

表1 用户项目评分矩阵Tab.1 User-Item scoring matrix

2.2 基于用户偏好的相似度

2.2.1 用户的兴趣偏好贴近度

在模糊数学中，贴近度可以用来表示2个集合的贴近程度，若2个模糊集合距离越大，贴近程度越远，集合的相关性越弱。假设u=(u1,u2,u3…un)，则海明贴近度为

(1)

用户的兴趣偏好度可以通过项目评级表现出来，评分越接近的用户，他们喜欢某一物品的概率也会越大。所以可以通过贴近度算法来计算用户间的偏好。定义用户的评级项目L=(l1,l2,l3…lm)，u和v是L上的评分集合，则基于用户偏好的贴近度可以定义为

(2)

(2)式仅使用了用户共有评定项目，这只能反映很小一部分用户的真实状况，忽视了游离在共同项目之外的用户评分，未能全面把握用户的兴趣偏好。本文使用全局评分项目，扩大对用户兴趣偏好的查找范围。然后，考虑到稀疏数据上由于评分分布稀疏且不均匀，公式计算会偏大造成用户贴近度失真的问题，利用分层的思想把全局项目分成用户共同项目和用户本地项目。对于无共同评定部分计算，使用平均评分填充。计算表达式为

(3)

2.2.2 用户的评分偏好

每个用户都有属于自己的评分风格，有的用户可能不喜欢给高分，有的用户可能会给相同的评分，对同一喜好物品，不同用户基于自己的评分偏好，可能会给出不同的数值，这就会降低推荐的精确度。考虑到用户在全局的评分项，通过计算不同用户可能出现的评分概率分布用以处理用户评分偏好问题。用户的评级偏好定义为

(4)

(4)式中：P(u,v)的取值为[0,1]；φ表示用户对物品的评分取值范围；l(u)与l(v)表示用户对所评分物品的数目；Φn与φm表示评分φ在u，v用户的物品评分列表中出现的次数之和。(4)式反映了在离散区间内，不同用户全局评分的概率分布的密度。对(4)式进行举例演示，假设u=(0,0,1,0,0,2,0,0,3,0,0,4,0,0,5)，v=(1,2,0,2,3,0,3,3,0,4,5,0,5,3,0)是项目的评级数据，其中评级值是1—5，根据(4)式，可以得出

(5)

2.2.3Jeffries-Matusita距离的组合相似度

Jeffries-Matusita距离[15]广泛用于各种领域，如图像处理，信号和模式识别等。对于度量距离较小的2个分量，会反映出较差的可分性，从而得出精度不高的结果。在协同过滤中，该距离可以用来计算用户的相似度，所以可以利用Jeffries-Matusita算法把用户在全局实际评分中的偏好度转化成用户间的相似度，表示为

(6)

2.3 基于共同评分项的相似度计算

2.3.1 基于logistic函数的惩罚因子

在推荐系统中，不同用户之间的共同评定项目的数量变化很大。评级越多的项目，从中提取的信息越多，相似度计算结果就越准确。因此，共同评定项目数量的比例是一个非常重要的影响因素。本文引入logistic函数对用户的共同评分项进行线性映射，得到一种关于共同评定的限制性惩罚因子，如果用户共同项目越少，得分就会越小。模型表示为

(7)

2.3.2 加权JMSD算法

JMSD算法考虑了用户的共同评级和项目信息，但是如前文所提问题一样，该算法过度依靠用户的共同项目，未能考虑到全局信息，在稀疏的数据下，用户共同项目较少，用户对项目评级缺失，共同评级计算难度大，这会造成相似度计算不准确。结合(7)式，对JMSD算法进行加权得

simJM(u,v)=Qu,v×JMSD

(8)

2.4 改进协同过滤算法ED-JM

加权JMSD算法使用用户的绝对评级信息和共同评级的比例，这是偏好度算法没有考虑到的地方。使基于用户的偏好度算法与加权JMSD算法相结合，可以充分利用他们的优点。最终得出本文算法模型为

simED-JM(u,v)=D(u,v)+simJM(u,v)

(9)

(9)式通过考虑用户兴趣偏好贴近度和用户的评分偏好，有效地使用共同评级项目和所有评级信息，这解决了在稀疏数据中，常规度量中找到相似性的参数仅考虑共同评定项目的实际评级信息而造成的共同评定问题；最后，结合加权JMSD算法对用户的绝对评级信息和共同评级的比例，提高了协同过滤算法的准确度。具体算法流程如图1。

图1 算法公式流程图Fig.1 Algorithm formula flow chart

2.5 评级预测

相似度计算完成后，预测表达式可以表示为

(10)

(10)式中，Nu表示用户u的最近邻居集合。该方法可以计算目标用户的所有未评级项目[16]。然后，推荐算法将前N个项目推荐给目标用户作为推荐结果。

3 实验对比分析

3.1 评价标准

推荐系统中推荐精度的评价标准有多种，现阶段使用最广的是平均绝对偏差MAE和均方根误差RMSE等[17]方法进行精度评估。MAE和RMSE的值越小表明推荐越精确越高，MAE用于估计实际评级与预测评级之间的平均绝对偏差，用pui和rui分别表示用户u在项目i上的预测评级和实际评级。MAE可以定义为

(11)

RMSE用来表示实际评级与预测评级之间的均方根误差，定义为

(12)

3.2 实验分析与结果1

本次实验采用的数据集是Movielens 100 K。Movielens 100 K含有943名用户对1 682部电影的100 000次评分，其中评分为5分制，稀疏程度为93.7%。其中，MAE，RMSE覆盖的性能值是基于邻居数K的数值计算的，K的值定义为10到100，间隔为10。

图2和图3分别展示出了在Movielens 100K的数据集上不同的相似性度量在不同K值下MAE和RMSE的对比。从图2和图3中可知，JMSD算法和修正的余弦算法明显不如其他算法，除了以上2个算法外，其他算法的函数曲线相对稳定，随着K值增加，算法准确率不断上升，之后略有下降。相比于性能较好的MCF算法[8]与COS算法，本文模型算法ED-JM在MAE指标上分别提高了2.1%和1.86%，在RMSE指标上分别提高了4%和3.68%。

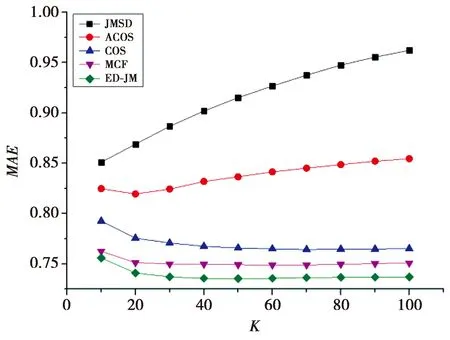
图2 在Movielens100 K下不同相似性度量的MAE对比Fig.2 MAE comparison of different similarity measuresunder movielens 100 K

图3 在Movielens100 K下不同相似性度量在RMSE对比Fig.3 Comparison of different similarity measures in RMSE under Movielens 100 K

3.3 实验分析与结果2

数据的稀疏性可能会使协同过滤算法的精度降低，为进一步验证所提算法，采用更为稀疏的数据集FilmTrust进行实验。FilmTrust数据集是一个小型的公开数据集。该数据集在2 071部电影中有1 508位用户拥有35 497个评分，其值为0.5的倍数，范围从0.5到4。FilmTrust的稀疏度为98.86%。在实验方面，使用COS算法、JMSD算法和MCF算法进行对比。

表2为不同算法在邻居数为[10，20，40，80，100]上不同的MAE值。

表2 不同相似度对应的MAETab.2 MAE values for different similarities

表3展示了3种相似度与本文算法在MAE上平均和最小的误差对比。

表3 算法误差对比Tab.3 Algorithm error comparison

由于FilmTrust数据集展现更为稀疏的特性，从表2、表3可知，随着K值增加，算法误差逐渐变大。JMSD算法准确度的高低和用户项目数有关，所以该算法相比其他算法依旧有着较差的MAE；传统协同过滤算法COS只考虑用户共同项目，所以在稀疏数据下整体性能较差，如表3，余弦算法最低误差率达到14.89%，该点在全图中有着最大误差。MCF的平均误差率为4.39%，相比Movielens 100 K实验可以发现，MCF算法对比所提算法性能有所下降。从图4可知，所提算法明显优于其他算法，在K=10的时候，本文算法精度要略低于MCF算法，但随着邻居数增加，算法要优于MCF算法并在K=40取得最优点。由此可见，本文算法在稀疏数据下也会有着高的准确率。

图4 FilmTrust数据集下不同的MAEFig.4 Different MAEs in the FilmTrust dataset

4 结束语

传统相似性度量算法不能向稀疏数据集中的用户提供有效推荐，本文算法有效地利用全局所有评级信息，而非单纯考虑用户提供的共同评定项目值。该算法将用户的兴趣贴近度评分偏好考虑到相似度计算中，然后结合加权JMSD算法，得出一个基于用户偏好的改进协同过滤算法。通过实验表明，本文算法不仅缓解了稀疏性问题，算法的精度也要高于传统算法和文献算法。在未来研究中，要进一步优化推荐算法，提高算法的精确度，为用户提供更好的推荐体验。