一种多属性的时空数据聚类算法分析研究

王慧东，宋耀莲，田榆杰

(昆明理工大学 信息工程与自动化学院，昆明 650500)

0 引 言

时空聚类分析是时空数据挖掘领域的重要分支，是计算机科学与地球信息科学交叉领域中最前沿、最具挑战的研究课题之一[1]。其目的在于从时空数据库中提取具有相似特征的密集时空对象集合，它是从空间维度到时空维度的扩展。时空数据的可视化分析[2-4]同样是近年数据可视化研究领域的热点前沿，以可视环境下交互式挖掘分析实现问题可以更高效地表达数据包含的信息。

时空聚类在疾病异常趋势[5]、全球气候变化[6]、犯罪热点分析[7]、地理现象分析[8]等领域的研究中起到了重要作用，辅助用户更好地发现和分析事务发展变化的趋势和规律。赵其杰等[9]针对小样本及混叠类群提出一种密度-距离的新式聚类优化方法；李晓璐等[10]针对具有密度分布非均匀特征的数据集，提出基于高斯混合模型的DBSCAN聚类算法分析车站内乘客的聚集特征；XIE等[11]针对DBSCAN算法聚类精度的问题，提出了一种设定参数的新方法来提高聚类的准确率；BIRANT等[12]基于DBSCAN算法之上考虑了时间因素，并提出ST-DBSCAN时空聚类算法，但其人为参数设置过多，导致聚类结果随机性增大；JOSHI[13]等基于密度聚类思想，通过拓扑邻接关系定义时空邻域，进而定义时空核点进行扩展聚类，该方法主要针对时空数据进行聚类；PEI[14]等在密度分解思想上提出了WKN时空聚类算法，该算法减少了参数的设置量，但是该算法仅适用于三维时空数据，无法考虑非时空的属性因素。传统的时空聚类算法主要针对固定属性的时空数据进行聚类分析，并且现有算法中，阈值设定的主观因素较多，客观性不足，存在较大随机性，容易导致聚类结果不理想。

ST-DBSCAN算法只能处理固定属性的时空数据，本文首先对特征属性进行分类，再通过引入Gower相似系数、Dice相似系数与欧几里德距离构建多属性相似计算模型用于多属性的时空数据聚类分析；基于ST-DBSCAN采用人为设定阈值的方法存在较大随机性，本文提出一种绘制时空对象距离频数柱状图的方法来设定阈值；最后，结合北京市计算机行业职位招聘数据进行仿真实验。

1 ST-DBSCAN算法概述

ST-DBSCAN是基于密度的时空聚类算法，时空密度聚类是从空间密度聚类到时空维度的扩展，它将对象密度当作对象间相似计算的标准，把时空簇从一系列不同密度区域中提取出来。由于在空间维度的基础上多考虑了时间因素，所以该算法需要设定的聚类参数为3个：时间距离阈值temporal_threshold，空间距离阈值spatial_threshold和时空对象量阈值MinPts，前2个参数用于确定时空邻近域，后一个用来确定时空邻近域内的对象数量。算法基本步骤如下。

步骤1建立一个三维的时空数据库，库中时空对象的经度为x，纬度为y，时间为t，一条时空对象数据为一个对象点Pi={idPi,xi,yi,ti}，i为时空对象序号，所有对象点的集合为DP；

步骤2从DP中依次选取一个对象点Pi，判断其是否已属于现有簇中，是则重新选取下一个对象点，否则进行步骤3；

步骤3判断对象点Pi是否为时空核心对象，是则进行步骤4，否则回到步骤2中重新选取下一个对象点；

步骤4搜寻时空核心对象点Pi的所有时空相邻点Qi，若Qi不属于任何已有的簇，则将Qi放入新建的簇中，若Qi属于已有的簇，则不进行操作；

步骤5判断簇A中新加入的对象是否为时空核心对象，若非时空核心对象，则将其标为边缘时空对象不进行进一步操作，是则对该时空核心对象重复步骤4的操作；

步骤6重复步骤2—步骤5的工作，直到DP中所有对象都属于某个簇，或为时空孤立点。

ST-DBSCAN算法只限于处理固定属性的时空数据分析，且在阈值设定上存在较大随机性容易导致其将噪声归到时空簇中或忽略部分低密度的簇。

2 改进的多属性时空聚类算法

2.1 特征属性分类

本文将时空事件数据对象定义为P={idP,x,y,t,Att}，其中，idP表示P的唯一对象标识符；x，y分别表示P对应的地理经、纬度坐标值；t表示P对应的具体时间值；Att表示P的属性特征集合。属性特征定义为attribute，用att表示，att∈Att，Att={att1,att2,…，attp}为P个不同属性特征的集合，attq={attq1,attq2,…，attqw}为第q个属性项里的w个不同属性值的集合。连续变量型的属性特征用attu表示，attu∈Attu，Attu={attu1,attu2,…，attuj}为j个不同连续变量属性特征的集合。有序分类变量的属性特征用attof表示，attof∈Attof，Attof={attof1,attof2,…，attofg}为g个不同有序分类变量属性特征的集合。无序分类变量的属性特征用attnf表示，attnf∈Attnf，Attnf={attnf1,attnf2,…，attnfh}为h个不同无序分类变量属性特征的集合。

2.2 多属性相似计算模型

为了计算具有多种不同类型属性特征的时空对象之间是否相似，本节提出了一种多属性相似计算模型。其模型计算式为

(1)

(1)式中：E表示具有连续变量属性特征的2个时空对象是否相似的结果；DG表示具有分类变量属性特征的2个时空对象是否相似的结果。其中，E与DG值的判断条件为

(2)

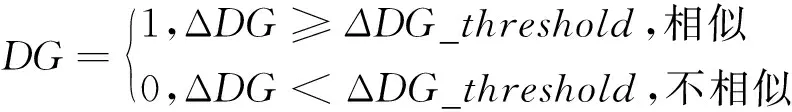
(3)

(2)—(3)式中：ΔE为具有多个连续变量属性特征的2个时空对象的相似距离，该距离越小，2个时空对象相似度越大；ΔE_threshold为连续变量相似度阈值，当ΔE≤ΔE_threshold(即E=1)时，2个时空对象相似；ΔDG为具有多个分类变量属性特征的2个时空对象的相似度大小，ΔDG值越大，2个时空对象相似度越大；ΔDG_threshold为分类变量相似度阈值，当ΔDG≥ΔDG_threshold(即DG=1)时，2个时空对象相似，且

(4)

(4)式中：ΔD与ΔG分别是具有多个无序和有序分类变量属性特征的2个时空对象之间的相似度值。多维的连续变量属性值之间的相似度距离通常采用欧氏距离计算方法，那么，2个时空对象中n维连续变量Attux={attux1,attux2,…，attuxn}间的相似度距离(即欧式距离)为

i∈[1,n]

(5)

将Dice相似系数应用于计算2个时空对象的无序分类变量属性值之间的相似度距离，表示为

(6)

2个时空对象中n维有序分类变量Attofx={attofx1,attofx2,…，attofxn}间的Gower系数为

i∈[1,n]

(7)

0≤δ(attofxi,attofyi)≤1

(8)

(7)—(8)式中，Ri为时空对象中第i个有序分类变量属性特征中值的极差。

2.3 阈值设定方法

本文提出通过绘制时空对象距离频数柱状图来设定时间与空间阈值的方法，需要计算空间距离ΔS与时间距离ΔT。若有2个时空对象点P1={idP1,x1,y1,t1}和P2={idP2,x2,y2,t2}，它们的时间距离为

ΔT=|t1-t2|

(9)

空间距离为

(10)

因本文后续研究中所采用的时空对象的位置均为实际地理位置即经纬度，故将(10)式演变为

ΔS=|Distance((x1,y1)-(x2,y2))|=

R×arcos[cos(y1)×cos(y2)×cos(x1-x2)+

sin(y1)×sin(y2)]

(11)

(11)式中，R为地球赤道半径。

该方法具体步骤如下。

步骤1计算时空对象事务集中两两时空对象在时间维度(或空间维度)下的时间(或空间)距离数值；

步骤2计算步骤1所得的各个距离大小值出现的频数；

步骤3将步骤2所得的频数数值对应纵轴，距离大小值对应横轴，绘制出时空对象距离频数柱状图，找出柱状图中最大距离频数数值对应的点，该点的时间(或空间)距离数值作为此维度下的时间阈值temporal_threshold(或空间阈值spatial_threshold)；

步骤4计算时空对象量阈值为

MinPts=ln(|DP|)

(12)

(12)式中，|DP|为时空对象点的总数。

2.4 算法流程

改进的多属性时空聚类算法的实现过程大致如图1。该算法共包括5个参数阈值：时间阈值temporal_threshold、空间阈值spatial_threshold、时空对象量阈值MinPts、连续变量相似度阈值ΔE_threshold、分类变量相似度阈值ΔDG_threshold。

图1 多属性时空聚类算法实现步骤流程图Fig.1 Multi-attribute spatial-temporal clustering algorithm implementation steps

算法流程如下。

步骤1建立一个多维度的时空信息数据库DP；

步骤2设置时空对象量阈值MinPts，根据多维时空数据集画出时空对象距离频数柱状图，确定空间阈值spatial_threshold、时间阈值temporal_threshold；

步骤3从DP依次选取一个对象点Pi，判断其是否已属于现有簇中，是则重新选取下一个对象点，否则进行步骤4；

步骤4判断对象点Pi是否为时空核心对象，是则进行步骤5，否则回到步骤3中重新选取下一个对象点；

步骤5搜寻时空核心对象点Pi的所有时空相邻点Qi，若Qi不属于任何已有的簇，则进行步骤6，否则重新选取下一个Qi继续本步骤；

步骤6通过混合属性相似计算模型计算出Pi与Qi的混合属性特征是否相似，相似则将Qi放入新建的簇中，否则重新选取下一个Qi继续步骤5；

步骤7判断簇中的各对象是否为时空核心对象，是则对该时空核心对象重复步骤5的操作，否则将不再进行下一步操作；

步骤8重复上述步骤3—步骤7的工作，直到DP中所有对象都属于某个簇，或为时空孤立点；

步骤9将上述得到的簇标签赋值给数据库新建的字段“簇标签”中。

3 实验结果及分析

3.1 阈值设定实验分析

本文随机生成了一组数据集来验证该方法的准确性。该数据集共有1 100个时空对象点，每个时空对象点有x，y，t3个值，x，y值分别对应地理经纬度坐标(即X，Y轴)，t对应时间月份(即Z轴)。如图2，黑点的集合即为实验数据集，图2中有2个黑色点密集区域，它们为密度相同、形状不规则的待验证时空簇，共计900个点；剩余的210个噪声点散布在密集区域周围，即离散区域。

图2 实验数据集散点图Fig.2 Scatter image of the experimental data set

为了判断聚类结果的好坏，本文将密集区域中被标记为时空簇的点数量占密集区域中所有对象点总数的百分比称为正标率，将离散区域中被标记为时空簇的点数量占离散区域中所有对象点总数的百分比称为误标率。正标率越大，且误标率越小，则说明该阈值设定得越合理。

绘制出该时空数据集的时空对象距离频数柱状图部分截图，如图3。

图3中时间和空间距离频数最大数值分别对应(4，15 830)和(5，3 349)点，即时间阈值temporal_threshold=4，空间阈值spatial_threshold=5，时空对象量阈值MinPts=ln(1100)≈7。通过ST-DBSCAN算法在4组不同阈值设定条件下对该数据集进行聚类分析，得出的聚类结果如图4。

图3 时空对象距离频数柱状图(部分截图)Fig.3 Spatial-temporal data object distance frequency columnar image

图4 实验数据集在4种阈值条件下的聚类结果图Fig.4 Clustering results of experimental data sets under four threshold conditions

图4的4幅聚类结果中，黑色点集群代表噪声(即时空独立点)，不同彩色点集群代表不同时空簇。图4a中3个阈值均是本文所提方法来设定的，并将该方法所得阈值条件下的聚类结果图作为参照图与另外3个阈值条件下的聚类结果图进行对比。图4b—图4d是在图4a所设定的阈值基础上分别对时空对象量阈值MinPts、空间阈值spatial_threshold、时间阈值temporal_threshold做了修改。从图4a可以看出，该时空数据集中的待验证时空点有98.5%分别被蓝色和红色标记出来，噪声点被标记为时空簇的概率为1.38%，可见该阈值下的聚类结果较好；图4b和图4c将原本同属于某一密度的时空簇被分为了多个不同密度的时空簇，导致正标率较低，聚类结果有较大误差；图4d将2个时空簇周围的多个噪声点也纳入了簇中，使得误标率较大，聚类结果精确度降低。通过该实验分析，可以确定本文所提出的设定阈值的方法具有较强的合理性与准确性。

3.2 多属性时空数据聚类分析

本文使用某主流招聘网站上发布的3 114条北京市计算机行业职位招聘数据构建了实验样本数据库。其中，时间、经纬度的数据格式符合要求，不用进一步处理；“五险一金”属于无序分类变量类型，其值的标识符可定义为0，1形式，0代表没有，1代表有；“学历”为有序分类变量类型，其值的转换定义如表1；为了能计算连续变量对聚类结果的影响，本文将职位数据中的“薪资”按照其数值所在区间生成随机整数，从而将薪资数据转换为类似连续变量的类型。

表1 学历值的转换定义对应表Tab.1 Educational conversion value correspondence table

职位数据集在时空维度及“五险一金”“学历”“薪资”属性特征条件下进行多属性时空聚类分析，聚类后的结果如图5，黑色点表示时空独立点，即噪声；不同的彩色点集表示不同的时空簇；因生成的簇数量较多，选取前10个体积较大的时空簇来进行结果分析；在三维坐标中，X轴为纬度，Y轴为经度，Z轴为时间(12个月)。

图5a为10个彩色时空簇和黑色时空独立点分布情况经纬度斜视图，为方便观察，图5b中只显示时空簇的分布情况。为进一步分析含有“五险一金”“学历”“薪资”的职位数据在聚类后的结果，此处将各个时空簇中“五险一金”“学历”“薪资”的情况用表2，表3展示出来。

表2 各时空簇中“五险一金”与“薪资”的数据统计Tab.2 Statistical results of different“five social insurance and one housing fund” and “salary” attributesin each spatiotemporal cluster

表3 各时空簇中“学历”的数据统计Tab.3 Statistical results of “educational background” attributes in each spatiotemporal cluster

图5 职位数据集在多属性条件下的时空聚类结果图Fig.5 Spatial-temporal clustering results of data sets under multi-attribute conditions

从图6可以看出，10个时空簇中有“五险一金”的比例都比较高，仅簇1、簇20相对较低，结合这2个簇在图5中的分布情况，可以分析出：在1月到2月期间的海淀区、昌平区一带以及八月的西城区、宣武区、崇文区一带，计算机行业职位招聘条件中有“五险一金”的几率相对较低一些；学历要求较高的是簇12、簇19、簇21和簇29，几乎都要求大专以上学历，学历要求较低的是簇3和簇20；薪资待遇方面，簇12、簇21和簇29的薪资待遇较好，大部分都在8 000～12 000元/月。综合上述分析结果得出：计算机行业职位招聘要求大专以上学历，有五险一金；待遇较好的职位集中于7月的西城区、崇文区和11月的西城区，以及11月、12月的朝阳区、东城区。

4 结束语

时空数据挖掘作为数据挖掘的拓展，不仅考虑到了空间因素，还考虑到了时间因素，主要是侧重于对空间对象进行动态性研究，以发现隐藏在动态空间对象下的规律模式和知识，目前已经受到各个行业的极大关注。

时空聚类分析是时空数据挖掘方向较为前沿，且技术不够完善的分支领域，本文通过研究分析当前时空聚类算法的国内外研究现状与其存在的问题，从以下2点进行深入研究：①根据已有的时空聚类算法ST-DBSCAN在人为设定阈值上存在较大随机性，从而导致聚类结果不理想的问题，本文提出了一种通过绘制时空对象距离频数柱状图的方法来合理设定阈值，通过仿真实验证明，新的阈值设定方法能够更为准确地识别出部分低密度簇，提高了聚类的准确性；②针对ST-DBSCAN算法仅限于对固定属性的时空数据进行聚类分析提出了一种新的改进型多属性时空聚类算法，实验结果表明，在加入了无序变量、有序变量和连续变量的条件下，该算法能够针对多属性的时空数据生成理想的聚类结果，在现实生活中具有很好的实用性。