EEMD-ARIMA在干旱预测中的应用——以新疆维吾尔自治区为例

许德合，丁 严，张 棋，黄会平

（华北水利水电大学，郑州450000）

干旱灾害是常见的自然灾害之一，其发生的主要原因是一段时期内降水量的减少，若遇到高温、大风和低温等异常气候，则会进一步加重干旱程度［1］。通常情况下，长时间的干旱将导致地区水资源供应不足，影响正常的农业生产和经济发展，造成不可估量的经济损失［2］。因此，如何对干旱的发生情况进行准确评估、监测和分析，成为了国内外学者研究的热门议题［3，4］。在对干旱进行研究的过程中，常使用易于进行对比分析和计算的干旱指标来评估干旱程度、持续时间和影响范围［5-7］。常用的干旱评价指标有标准化降水指数（Standard Precipitation Index，SPI）、标准化降水蒸散指数（Standard Precipitation Evaporation Index，SPEI）、帕默尔干旱指数（Plamer Drought Severity Index，PDSI）等［8-13］，其中SPI的运用最为广泛。SPI是用来描述一段时间内降水量出现频率多少的指标，可应用于不同时间尺度下的计算，干旱分级精度相对较高［14-16］。不同时间尺度的SPI能够反映不同类型的干旱，1个月时间尺度的SPI适用于季节干旱的分析，6 个月时间尺度的SPI可用于分析农业干旱，长时间尺度的SPI适于分析水文干旱。

近几年，国内干旱灾害时常发生，其中以西北地区最为严重［17］。对新疆维吾尔自治区不同地区的干湿变化进行研究，探索不同时期的降水量对区域产生的影响，明确干旱的成因机制，可为相关部门在制定有效干旱应对措施时提供帮助，减少干旱灾害所带来的经济损失［1］。目前，常用的干旱预测模型有差分自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）、支持向量机（Support Vector Machine，SVM）等。其中ARIMA 模型是最常用的数据驱动模型，常用于时间序列数据的预测。韩萍等利用ARIMA 模型对多个时间尺度的SPI进行预测，并对模型预测结果进行对比分析，得出ARIMA 模型较适合SPI3、SPI6、SPI9序列的短期预测，适合SPI12、SPI24序列长期预测的结论［18］；李佳佳等为识别长江流域月降水周期振荡和长期趋势的显著影响因子，应用集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）方法，分别对各站点的月降水序列进行分解［19］；王佳等基于EEMD-ANN（Artificial Neural Network，ANN）预报模型预测入库径流量，结果表明使用EEMD-ANN 可以较为精准地进行径流量预测［20］；李辉等为提取机组故障特征，将EEMD 与SOM 神经网络结合进行故障自动识别，结果表明该方法可以准确提取机组故障特征且计算速度快［21］；李勃旭等为确定地铁门传动系统的退化状态，采用EMD-ARIMA 模型对夹紧力峰值的均值和标准差进行预测，结果表明EMD-ARIMA 模型能够较好的预测夹紧力的峰值［22］。利用气象站点监测到的降雨量值计算得到的SPI序列属于典型的非平稳时间序列，而ARIMA模型能够更多的提取原始序列的信息，常用于处理非平稳的时间序列，因此可以利用ARIMA模型预测SPI序列［23］。EEMD 能够提取出原始信号在不同尺度的局部特征信号，精准地反映出原时间序列信号的物理特性，从而为模型预测提供稳定的前提。EEMD-ARIMA 模型集合了EEMD 和ARIMA 模型的优点，通过EEMD 分解得到时间序列平稳的局部特征，有利于ARIMA 模型的预测，可以提高模型的预测精度。因此，本文利用EEMD-ARIMA 组合模型对多尺度SPI序列进行预测，分析模型在干旱预测中的应用及优势，以期为干旱防控工作提供帮助。

本文通过对新疆维吾尔自治区32 个气象站点于1960-2019年间收集到的降水量数据进行计算，得到不同时间尺度的SPI，通过ARIMA 模型和EEMD-ARIMA 组合模型，分别对1、3、6、9、12、24，6个时间尺度的SPI进行预测，并采用平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、决定系数（R-Square，R2）对两种模型的预测精度进行评价。由于计算处理的数据量大，受论文篇幅限制无法展示所有数据的处理结果，加之本文侧重于讲述组合模型在干旱预测中的优势，故在文中仅以分布在整个新疆地区3 个不同方位上的福海站、巴音布鲁克站、莎车站为例，分析组合模型的预测结果，并进行两种模型预测结果的对比和分析。两种模型对32 个站点多尺度SPI的预测结果，结合ArcGIS 的经验贝叶斯克里金插值法在文末进行可视化展示和分析。

1 研究区概况

新疆维吾尔自治区地理坐标介于34°25'N～48°10'N、73°40'E～96°18'E 之间。省域内平均海拔约1 000 m，区域北部有阿尔泰山，南部有昆仑山系，省域中部的天山以北为准噶尔盆地，南部为塔里木盆地。新疆维吾尔自治区远离海洋，区域地形复杂，四周高山环绕，海洋气流不易到达，致使区域内气候干燥，是典型的干旱、半干旱地区。区域年平均降水量在150 mm 左右，区域北部的降水量高于南部，各地降水量相差很大。受气候和地理环境的影响，新疆维吾尔自治区生态环境脆弱，各种自然灾害频繁发生，在全球气候变暖的形势下，干旱灾害产生的影响呈现出扩大化的趋势［24，25］。

图1 研究区域及气象站点分布Fig.1 Distribution of meteorological stations in study area

2 数据来源与方法

2.1 数据来源

本文所用逐日降水量数据来源于国家气象科学数据中心（http：//data.cma.cn/）中新疆维吾尔自治区气象站观测数据。所用新疆维吾尔自治区地理高程数据来源于地理空间数据云（http：//www.gscloud.cn/search）。表1 为所选3 个示例站点的信息。

表1 示例气象站点信息Tab.1 Information of sample meteorological stations

2.2 研究方法

2.2.1 标准化降水指数（SPI）

近年来，国内外学者常使用SPI指数进行气象干旱研究。SPI指数是通过计算出某时段内降水量的Γ 分布概率，经正态标准化处理后，根据处理结果划分干旱等级。它可以用来反映一段时间内降水量出现频率的多少，易于计算且能直观反映气象干旱的程度［26］。SPI的具体计算过程参见气象干旱等级（GB/T20481-2017）。依据国家标准气象干旱等级（GB/T20481-2017）规定的干旱分级标准（表2），根据计算得到的SPI，确定区域的干旱类型。

表2 标准化降水指数干旱分级Tab.2 Drought classification based on SPI

SPI1、SPI3、SPI6、SPI9、SPI12、SPI24分别对应1、3、6、9、12、24个月时间尺度的SPI。短时间尺度的SPI常用来反映短期内的降雨量变化。SPI1适用于气象干旱，可用于反映短期降水变化情况。3个月时间尺度下的SPI用来描述降雨量的季节变化，计算出的SPI3中5、8、11、2月数据可分别用于描述春、夏、秋、冬的干旱情况。6 个月时间尺度下的SPI适用于农业干旱。长时间尺度的SPI常用来分析长期的干旱趋势。SPI9可用于表征较长时间内的地下水位变化。SPI12的时间周期较长，能较清楚的描述年际降雨量变化情况，24 个月时间尺度的SPI序列则用于分析长期的降水变化所引起的干旱［27-29］。

2.2.2 ARIMA模型

自回归移动平均模型（Auto-Regressive and Moving Average Model，ARMA）的建模思想是将预测值假定为一组随机序列，确定能够近似描述这组序列的模型，之后根据该序列的过去值和现在值，对未来值进行预测［30］。ARMA 模型分为自回归模型（Auto-Regressive，AR）、滑动平均模型（Moving-Average，MA）以及ARMA。只要是平稳且非白噪声的时间序列皆可通过建立ARMA 模型进行预测，但大多数时间序列都是非平稳时间序列。因此，在时间序列具有某种趋势时，需要对时间序列进行d次差分，使其成为平稳序列。进行d次差分后的ARMA 模型即为ARIMA模型。ARIMA（p，d，q）模型的一般式为：

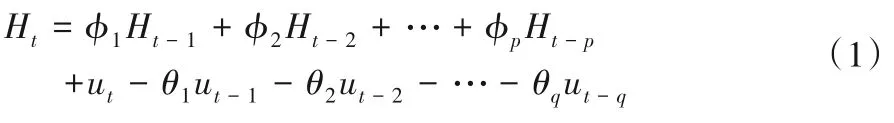
式中：Ht为时间序列值；φi(i= 1，2，…，p)和θj(j= 1，2，…，q)分别为自回归系数和滑动平均系数；ut为白噪声序列，且ut～N(0，σ2)。

ARIMA模型建模流程为：

（1）平稳性检验。本文使用单位根检验（Augmented Dickey-Fuller Test，ADF）法进行判断。在ADF 检验中，原假设为非平稳时间序列且存在单位根，给定显著水平α=0.05，若检验统计量对应的概率值（P）小于0.05，则拒绝原假设［31，32］。对于非平稳的时间序列需要进行差分，得到平稳序列。

（2）p、q取值范围确定。根据数据的自相关函数和偏自相关函数来确定模型阶数p、q的取值范围。

（3）模型定阶。采用赤池信息准则（Akaike Information Criterion，AIC）、贝叶斯信息准则（Bayesian Information Criterion，BIC）进行模型定阶，AIC、BIC公式如下：

式中：N为参数个数。

在不同p和q组合的模型中，选择AIC、BIC的最小值所对应的参数，从而得到最优ARIMA模型。

2.2.3 EEMD分解

1998年N E Huang 等人提出了经验模态分解（Empirical Mode Decomposition，EMD），EMD 能够完美地适应于全部的非线性、非平稳信号的处理，并且经过该方法处理后的结果具有相当高的信噪比［33］。原始序列输入EMD 后得到有限个固有模态函数（Intrinsic Mode Function，IMF）和余量，各IMF分量包含了原始序列不同时间尺度的局部特征，尽可能地保留原始数据的 特 性［22］。EEMD 是EMD 的 一种改进方法，与EMD相比，EEMD在信号中加入了高斯白噪声，高斯白噪声以其均匀分布的特性补偿了IMF分量的损失，其步骤算法如下［34］：

（1）在原始数据Y(t)中添加正态分布的白噪声序列ωi(t)，试验次数为i；

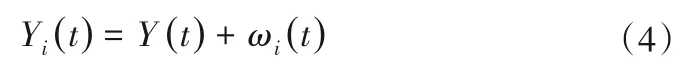
（2）进行EMD 分解，将含有白噪声的原始数据分解为IMF的组合；

（3）每次都加入服从同一分布的不同白噪声序列，重复步骤1和2，得到一组不同的IMF成分和残差；

（4）以所有IMF的均值作为最终的IMF组。

最终的分解结果为：

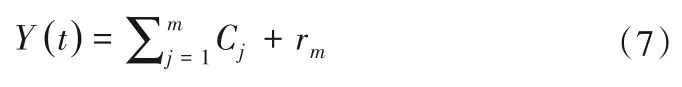
2.2.4 EEMD-ARIMA模型

通过Python编程语言，将EEMD 与ARIMA 模型结合为新的预测方法EEMD-ARIMA 模型。组合模型先利用EEMD 将有非平稳特征的时间序列SPI分解为N项含有原序列局部特征的序列，再利用ARIMA 模型对这些序列分别进行预测，最后把各项预测结果求和得到该序列的最终预测结果，这样的预测结果比直接用ARIMA 模型预测的非平稳时间序列SPI的结果具有更高的精度。使用EEMD-ARIMA模型进行预测的步骤如下：

（1）EEMD 处理。将降水量数据导入EEMD 进行分解，原始序列分解为从高频到低频的IMF1、IMF2、…、IMFn以及残差量。残差量即趋势，将其记为IMFn+1。

（2）ARIMA 模型处理。将IMF1、IMF2、…、IMFn+1，分别导入ARIMA模型进行预测，对各个分量进行平稳性检验和模型定阶，并将预测结果输出。预测结果记为P1、P2、…、Pn+1。

（3）对P1、P2、…、Pn+1进行相加求和。

EEMD-ARIMA模型建立流程见图2。

图2 EEMD-ARIMA模型建立流程Fig.2 EEMD-ARIMA combined model forecast flow chart

2.3 评价指标

常见的回归预测评估指标有MAE、均方误差（Mean Square Error，MSE）、RMSE，其中MAE和MSE是基础的评估指标，RMSE是MSE指标的扩展，相较MSE指标更加准确。为了比较各模型预测精度的高低，本文选定了RMSE、MAE和R23 种评价指标对ARIMA 模型和EEMD-ARIMA 组合模型的预测结果进行评价。RMSE是用来衡量观测值与真实值之间的偏差，MAE是绝对误差的平均值，能够更好地反映预测值误差的实际情况，RMSE和MAE的值越小，模型效果越好。R2是将预测值与均值进行对比，R2越大，表示拟合效果越好，最大值为1。

式中：xi是观测值；yi是真实值；是yi的平均值为预测值；N为样本数。

3 结果与分析

3.1 ARIMA模型建模和预测

依据国家气象信息中心提供的中国地面气候资料月值数据集，选择1960-2019年新疆维吾尔自治区境内32 个气象站点持续测定的逐月降水量数据，进行多尺度SPI的计算。由于SPI在不同时间尺度适用于不同种类的干旱，因此选取了1、3、6、9、12、24 共6 个时间尺度［18］。将计算得到的SPI序列，分别记为SPI1、SPI3、SPI6、SPI9、SPI12、SPI24。

通过Python3.6 对ARIMA 建模。经过ADF 检验，SPI1、SPI3、SPI6、SPI9、SPI12、SPI24的P值均小于0.05，故为平稳时间序列。通过ACF、PACF进行模型定阶，选择当AIC、BIC值最小时对应的p、q值［35］，各序列的模型定阶结果见表3，即为各时间尺度的最优模型。选取1960-2007年数据作为训练集，2008-2019年数据作为测试集。应用32个气象站点各时间尺度的ARIMA 最优模型对SPI序列进行预测。示例站点的预测结果分别见图4、图5和图6。

表3 六尺度SPI序列的ARIMA模型定阶Tab.3 Order the ARIMA model based on six scales SPI values

3.2 EEMD-ARIMA模型建立和预测

EEMD能够将原始信号逐级分解并提取出其在不同尺度的局部特征信号，从而准确反映出原时间序列信号的物理特性。在分解过程中，需要对Nstd和NE进行设置。Nstd用于设置添加高斯白噪声的标准差，取值范围一般为0.01～0.4，具体设置数值根据原信号中的噪声干扰大小，视具体情况确定。NE是添加噪声的次数，通常取值为50或100。利用EEMD对多尺度SPI进行分解，经过多次参数修改及其分解结果的对比，最终将Nstd设置为0.2，NE设置为100。将加入白噪声序列的原始序列进行分解，得到8 个IMF分量和1 个残差数据，如图3 所示为对福海站SPI3序列进行EEMD 分解得到的结果。从图3 中可以看出，分解出的时间序列均围绕0 值上下波动，趋于平稳，说明通过EEMD进行分解能够降低原始序列的非平稳性。

图3 EEMD分解结果Fig.3 EEMD decomposition results

选取1960-2007年数据作为训练集，2008-2019年数据作为测试集。将EEMD 分解得到的1960-2007年数据输入ARIMA 模型进行预测，并以ARIMA 模型预测结果之和作为预测的最终结果。将6 个时间尺度的SPI实际计算值、ARIMA 模型预测值、EEMD-ARIMA 模型预测值进行对比展示。3 个示例站点的预测对比图分别为图4、图5和图6。

图4 基于ARIMA模型与EEMD-ARIMA组合模型对福海站多时间尺度SPI值的预测结果与观测值计算结果对比（2008-2019）Fig.4 Comparison of predicted and observed value of multi-time scale SPI of ARIMA model and EEMD-ARIMA combined model in Fuhai Station（2008-2019）

图5 基于ARIMA模型与EEMD-ARIMA组合模型对巴音布鲁克站多时间尺度SPI值的预测结果与观测值计算结果对比（2008-2019）Fig.5 Comparison of predicted and observed value of multi-time scale SPI of ARIMA model and EEMD-ARIMA combined model in Bayinbuluke Station（2008-2019）

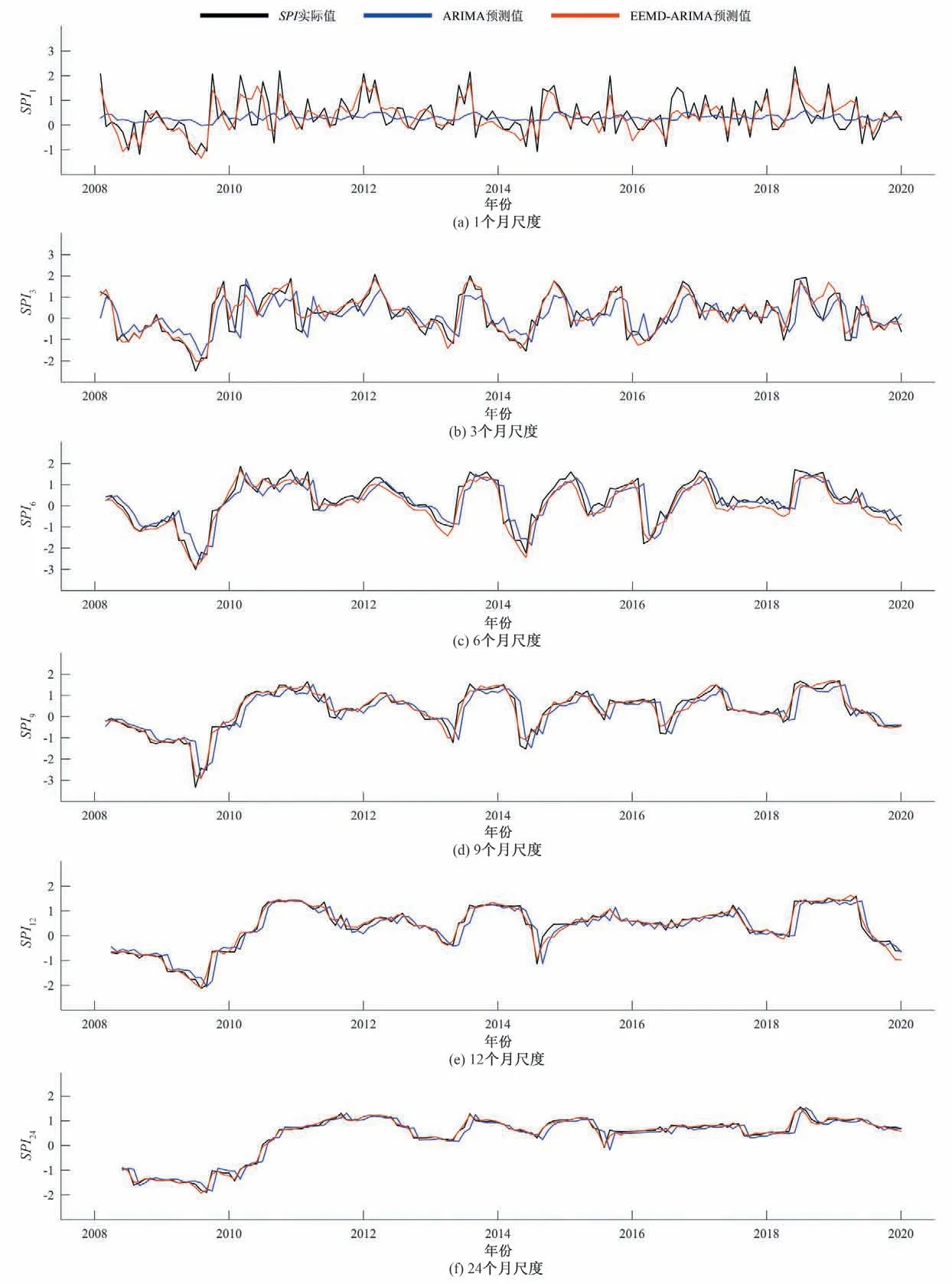
图6 基于ARIMA模型与EEMD-ARIMA组合模型对莎车站多时间尺度SPI值的预测结果与观测值计算结果对比（2008-2019）Fig.6 Comparison of predicted and observed value of multi-time scale SPI of ARIMA model and EEMD-ARIMA combined model in Shache Station（2008-2019）

由图4（a）可知，2010年、2012年、2018年，福海站旱情最为严重，EEMD-ARIMA 组合模型的计算结果与实际情况最为接近，较为精确的预测到了严重干旱的发生，在这些时间段中组合模型的预测值比ARIMA 模型的预测值更接近SPI实际计算值。在图5（a）中2018年，组合模型的预测结果更符合实际情况，这表明组合模型对极端天气预测结果的准确度要高于单一模型。根据组合模型的预测结果可知，3 个站点在2008年和2014年有严重干旱发生，这与新疆年鉴中对大范围干旱的记录一致。图4（b）2010-2011年，图5（a）2016-2017年SPI值异常，在快速增长后快速下降，对于这种异常变化，通过组合模型预测得到的干旱情况更接近实际的变化情况。根据图4、图5 和图6 的（c）、（d）、（e）、（f）图可以看到，两种模型的预测值均与实际计算得到的SPI值接近，但随着时间尺度的增大，单一模型预测结果延迟越发明显，在24 个月时间尺度，与实际计算结果相比有近一个月的延迟。而组合模型随着时间尺度的增大，预测结果与实际计算结果更为接近。从3个站点的多尺度SPI对比中可以明显看到，两种模型在1 个月时间尺度下的预测值与实际值有明显差异。在各时间尺度下，组合模型的预测值与SPI实际值之间的差值均小于单一模型预测值与SPI实际值的差值，表明组合模型在6 个时间尺度下均能更好的预测SPI序列。

为验证EEMD-ARIMA 组合模型和ARIMA 模型在6个时间尺度下的预测精度，通过MAE、RMSE、R2对两种模型在6个时间尺度下的预测结果进行了评价，结果见表4。RMSE和MAE的取值范围为［0，+∞］，取值越小，模型效果越好，当值为0 时，说明模型完美。R2取值越大，表示拟合效果越好，最大值为1，当值为1 时表明模型预测效果最佳。对比3 个站点在不同时间尺度下的组合模型和单一模型的MAE、RMSE、R2值发现，组合模型在任一时间尺度下的MAE、RMSE值均小于单一模型的值，且在任一时间尺度下的R2值均大于单一模型的值，说明EEMDARIMA 组合模型在各个时间尺度下的预测精度均高于单一模型，表明组合模型更适用于多时间尺度下的时间序列预测。组合模型在1个月时间尺度时，预测精度远高于单一模型，随着时间尺度的增加，两种模型预测精度之间的差距逐渐缩小，在24个月时间尺度时达到最小，表明组合模型在1、3 个月时间尺度下的预测结果远优于单一模型，在6、9个月时间尺度时，优于单一模型，在12、24 个月时间尺度下略优于单一模型。随着时间尺度的增加，SPI序列特征趋于平稳，ARIMA模型对序列的拟合效果逐渐提升。

表4 ARIMA模型和EEMD-ARIMA组合模型的MAE、RMSE、R2值Tab.4 MAE、RMSE and R2 values for ARIMA and EEMD-ARIMA models

结合ArcGIS的空间分析功能，利用经验贝叶斯克里金插值法对2019年32 个站点的SPI实际观测计算值和预测值进行可视化（如图7）。由于不同时间尺度的SPI适用情况不同，且新疆的春旱威胁最大，其次为夏旱和秋旱［36］，故此处选择能够进行降雨量季节变化分析的SPI3，对新疆维吾尔自治区春、夏、秋、冬的干旱情况进行插值可视化。从图7 中可以看到EEMD-ARIMA 组合模型在四季的预测结果与实际情况接近，较ARIMA 模型的预测结果更符合实际。

图7 基于SPI实际值、ARIMA模型预测值和EEMD-ARIMA模型预测值的季尺度干旱空间分布Fig.7 Spatial distributions of seasonal drought levels based on the actual values and the predicted results of models

4 讨 论

ARIMA 模型和EEMD-ARIMA 组合模型对SPI的预测精度随时间尺度的增加而提高，并在24 个月时间尺度时达到最高。从SPI的计算公式来看，随着时间尺度的增加，SPI序列中集合了原始数据中更多的信息，因此，预测值对实际计算值的拟合更为充分。从结果来看，EEMD-ARIMA 组合模型的预测结果比单一模型的预测结果更接近实际情况，这是因为通过ARIMA模型对多尺度SPI进行预测存在特征不平稳的情况，而EEMD可以通过提取出原始时序在不同尺度的局部特征，从而将SPI数据序列平稳化，为ARIMA 预测提供稳定的前提。因此，EEMD-ARIMA 组合模型优于单一模型，能够用于新疆地区的干旱预测。

新疆四季降水不均，四季的干旱情况不同，以春旱最为严重，秋旱和夏旱次之。因此，文中主要考虑了降水量对区域的影响，选取了3 个月尺度的SPI进行可视化展示。在对预测结果进行分析时，也侧重于对3 个月尺度的计算结果的分析。但河流、植物覆盖等都会对干旱情况产生影响，1978-2008年新疆耕地面积总体呈增加的趋势，农作物的增加对地区的水利设施造成负担，减弱了地区的抗旱能力，造成干旱程度的进一步加剧。在之后的干旱研究中，将通过对长时间尺度的SPI值的分析，进一步研究地下水位的变化，植被的覆盖等对干旱产生的影响。从不同尺度的SPI值进行研究得到更加准确详细的结果。

对极端干旱的预测是目前研究的热点和干旱预测问题的研究重点。本文利用SPI对新疆地区的干旱时空变化情况进行分析，基于计算出的数据，对EEMD-ARIMA 模型在新疆地区的干旱预测中的适用性进行研究发现，组合模型可以较好的捕获2008-2019年的干旱事件，适用于新疆地区的干旱预测。北疆和南疆的干旱情况有所不同，南疆大部分地区以农业为主，水利设施投入不足；而北疆的抗旱浇灌面积持续增长、农业和水利设施投入程度增加，因此南疆的受旱面积增长趋势大于北疆［37］。在后续的研究中，针对不同地区的实际情况，进一步细化干旱评价指标的选取，找出不同地区最为适合的干旱指数，提高模型在新疆的适用性。

5 结 论

本文基于新疆维吾尔自治区32个气象站点的降水量数据，计算出不同时间尺度下的SPI值，通过对SPI序列的分析、建模及预测，得到如下结论。

（1）单一的ARIMA 模型，在1 个月尺度下的预测精度最低，在24个月尺度的预测精度最高。主要是由两个原因造成的，其一，ARIMA 模型是一个整体线性自回归模型，随着预测数据的增多，精度会下降。在1 个月尺度下，通过ARIMA 模型得到的预测数据多于其他时间尺度，故精度相较其他时间尺度而言较低。其二，长时间尺度的SPI序列集合了更多原始数据的信息，有利于模型的预测。在不同时间尺度下，组合模型的预测精度均高于单一模型。

（2）EEMD-ARIMA 组合模型预测出的干旱发生年份与实际情况近似一致，能够用于对新疆地区干旱的预测。通过EEMD对数据进行分解，精简了模型对原始数据的读取过程，提高了预测精度。利用EEMD 对各尺度的SPI进行分解，得到一组比原始序列特征更加平稳的分量，将各分量导入ARIMA进行预测，并将各分量的预测结果累加得到每一时间尺度下的预测数据，得到的预测数据的精度均高于单一模型。从预测结果来看，EEMD-ARIMA 组合模型优于ARIMA 模型，即EEMDARIMA组合模型能够更好的拟合不同时间尺度下的SPI。

气象干旱能够为区域的干旱情况提供预警，气象站点监测到的气温、降水数据只能近似的反映区域的情况，粗略的估计区域的干旱变化情况，需要研究更加优化的干旱评价指标使其更精确的描述区域的变化情况。