基于SWAT模型和降水随机模拟的径流预测

张金萍，王宇昊

（1.郑州大学水利科学与工程学院，郑州450001；2.郑州大学黄河生态保护与区域协调发展研究院，郑州450001）

SWAT 模型基于物理过程建立，且能够充分反映流域内降水和下垫面要素空间变化对水文过程的影响，是研究流域水文循环的有效工具，是探究水文规律和机理的有效手段［1，2］。SWAT 模型在国内外应用广泛，包括对水质、径流、泥沙等方面的研究，其中最为常见的就是径流模拟［3］。例如王博威等依据四期土地利用数据构建SWAT 模型，从而分析土地利用变化对流域径流及其空间分布的影响［4］；廖亚一等将蒙特卡洛随机采样引入SWAT 模型，探讨气象数据输入不确定性对径流模拟结果的影响［5］；这些研究主要集中于通过构建SWAT 模型探究土地利用变化、人类活动、气候变化等因素对径流的影响［6，7］，但降水是气象数据中对径流模拟结果影响最大的因素，降水的总量和年内分布均会对径流过程造成较大的影响［8］，而对不同量级和年内分布降水情景相应径流过程的研究较少。

降水模拟包括降水概率的模拟和降水量的模拟，目前国内外运用比较多的降水概率模型主要有一阶Markov 链、高阶Markov链、间隔长度和半经验分布法4种，而分布模型广泛用于降水量模拟［9］。其中耦合Markov 链-Gamma 分布的随机模拟模型既能利用Markov链将降水日和非降水日相联系，也能在考虑降水年内分布不均匀的前提下利用降水的概率分布较好的模拟降水日的降水量［10］。例如王斌等应用模拟的降水序列，结合缺水率指标划分农业旱情等级［11］；秦道清等将比例调整算法引入随机模拟模型，生成日降水模拟序列［12］。但这些研究并没有考虑到不同降水量级下降水年内分布规律和模拟参数的差异性，因此根据年降水量级的不同分别构建随机模拟模型能有效提高模拟的代表性和准确性。

本文的创新点在于将降水随机模拟和SWAT 模型相结合，基于不同降水量级下降水年内分布规律和模拟参数的差异性，通过构建不同量级降水下的随机模拟模型，生成未来年降水量为800 mm（丰水）、550 mm（平水）、300 mm（枯水）相对应的日降水过程，并将其输入SWAT模型预测径流，从而进一步探究降水和径流的关系，具体流程见图1。

1 数据与方法

1.1 研究区域概况及数据来源

沙河属于海河流域大清河水系，发源于山西省灵丘县，流经河北省阜平境内，最后注入王快水库。王快水库以上流域控制面积为3 770 km2，主河道长166 km，占沙河流域6 420 km2的59%。该流域多为山区，地表植被覆盖较差，水土流失较为严重。王快水库以上流域地处中温带半湿润半干旱大陆季风气候区，多年平均气温12.5 ℃，最高气温41.7 ℃，多发生在7月份，最低气温-18.9 ℃，多发生在1月份［13］。

本文气象数据选用CMADS 数据集［14，15］在研究区域内及周边的15 个站点和阜平站的气象资料（最高、最低气温，平均风速，日降水量，相对湿度，日照时数），径流资料选用阜平水文站2008-2015年实测径流资料，研究区域地理位置和站点分布见图2。

图2 研究区域和站点分布Fig.2 Study area and distribution of stations

1.2 SWAT模型

SWAT 是一种基于物理机制的半分布式水文模型，该模型以日为时间步长，能够在不同的时间尺度（日、月和年）上进行连续的长时段的模拟，通常设计用于利用流域和流域尺度的输入数据对连续的长期径流、泥沙和农药产量进行建模和模拟［16］。SWAT模型将流域水文过程模拟分为水循环陆面过程和水循环水面过程，其中前者综合了气候、冠层截留、蒸腾蒸发、入渗、植被、地下水等产流和坡面汇流的影响因素，后者综合了子河道传输过程、主河道汇流、洼地滞蓄过程等河网汇流的影响因素。因此，相比集总式模型，SWAT模型对于流域下垫面非均质的描述更符合实际情况［17］，SWAT 模型的具体运行流程见图3。

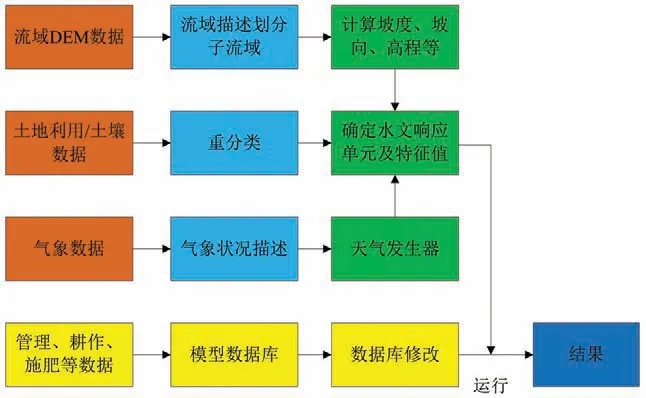
图3 SWAT模型运行流程Fig.3 Operating process of SWAT model

1.3 耦合Markov链和Gamma分布的降水模拟

一阶Markov 链模型将自然日分为降水日（P≥0.1 mm）和非降水日（P＜0.1 mm），模型的两个基本参数是非降水日转移到降水日的概率P（W/D）和降水日转移到降水日的概率P（W/W）。研究表明当月的两个状态转移概率值均与同月降水日出现频率q密切相关且存在线性关系，且转移概率可用下式估算［18］：

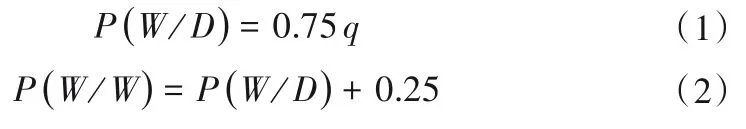
若连续型随机变量X服从Gamma 分布，则X的密度函数为：

式中：α为形状参数，决定了Gamma 分布的形状；β为尺度参数，决定了Gamma 分布的分散度。一阶Markov 链模型的两个转移概率值和Gamma分布的两个参数合称为降水模拟参数。

随机模拟步骤如下：

（1）以1月为例，假设1月1日为非降水日，在确定模拟参数的基础上，将计算机产生的［0，1］之间的随机数和P（W/D），P（W/W）进行比较。

（2）当前一日为非降水日时，若随机数大于当月的P（W/D），则当日仍为非降水日，反之则为降水日；前一日为降水日时，若随机数小于当月的P（W/W），则当日仍为降水日，反之则为非降水日；

（3）当日为降水日时，将当月降水的Gamma 分布结合随机数产生当日降水量。以此类推，即可产生若干年的逐日降水序列［19］。

2 SWAT模型的构建

2.1 基础数据库的构建

除气象数据和径流数据以外，SWAT 模型的构建还需要流域的地形高程数据、土地利用数据、土壤分类数据等资料。其中地形数字高程图（DEM）来源于地理空间数据云，分辨率为30 m；土地利用数据选取2015年全国土地利用数据，分辨率为30 m；土壤数据来自HWSD 全球土壤数据库1∶100 万中国土壤数据集。此外，由于水库位于流域出口位置且研究区域多为山区，人类活动对研究区域内水文循环过程的影响较弱，因此在SWAT模型中可忽略不计。

根据DEM 图提取坡向、坡度数据，生成王快水库以上流域河网，并根据设定的临界集水面积将王快水库以上流域划分为14 个子流域（图4），其中阜平水文站位于5 号子流域的出口；对流域内的土地利用/覆盖数据进行重分类，共分为耕地、林地、草地、水域、城乡工矿居民用地、未利用地等6个种类；以HWSD土壤数据集为基础，结合SPAW软件计算土壤层有效持水量、土壤湿密度等参数，完成土壤数据库的制作并对土壤进行重分类，共分为26 个种类，其中土地利用分类和土壤分类见图5。根据土地利用、土壤、坡向设置，共划分水文响应单元（HRU）119个。

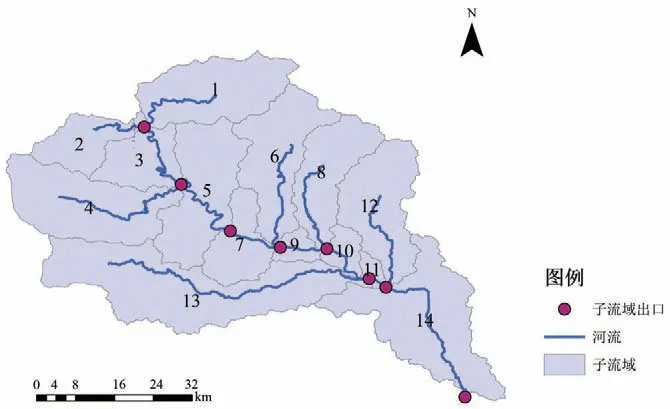
图4 子流域划分Fig.4 Watershed Subdivision of study area

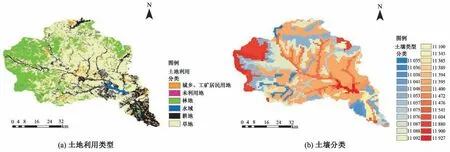
图5 土地利用分类和土壤分类Fig.5 The classification of land use and soil

2.2 参数敏感性分析

在模型初步构建完成后，应当在其运行结果的基础上进行参数敏感性分析，从而确定该模型中对径流模拟影响较大的参数，以此为依据求解使模型模拟效果最佳的参数组合。本文依托SWAT-CUP 软件的SUFI2算法进行参数敏感性分析，参数的相对显著性可由t-Stat检验值确定，其中t-Stat检验值的绝对值越大，参数敏感性越高［20］。选取影响径流的28 个参数［21］，将模型输出结果和阜平水文站的实测径流数据结合，进行1 000 次迭代运算，挑选敏感性排名前17 的参数进行下一步的率定，敏感性分析见表1。

表1 参数敏感性分析Tab.1 Parameter sensitivity analysis

由表1 可得：各参数对径流模拟结果均有不同程度的相关性，其中最为敏感的参数是湿润条件下的初始SCS 径流曲线数，该参数的大小代表着下垫面不透水性的强弱，即CN2 值越大，径流量越大；第二敏感的参数为地下水延迟时间，反映的是基流快慢，对水文过程有重要影响；此外，土壤饱和容重、最大冠层截留量等参数对模型输出结果的影响也较为显著。

2.3 参数率定与验证

将2008，2009 作为预热年份，选用阜平水文站2010.1.1-2012.12.31 的实测流量对模型进行参数率定，本文选取决定系数（R2）、纳什效率系数（NSE）、相对误差（Re）3 个指标用于评价模型的模拟精度，R2和NSE越接近1，Re越接近0，模拟效果越好。一般来说，当模拟结果满足R2＞0.6，NSE＞0.5，|Re|≤20%时视为模拟结果可信；当模拟结果满足R2＞0.7，NSE＞0.65 时视为模拟结果良好［22］。计算公式分别如下：

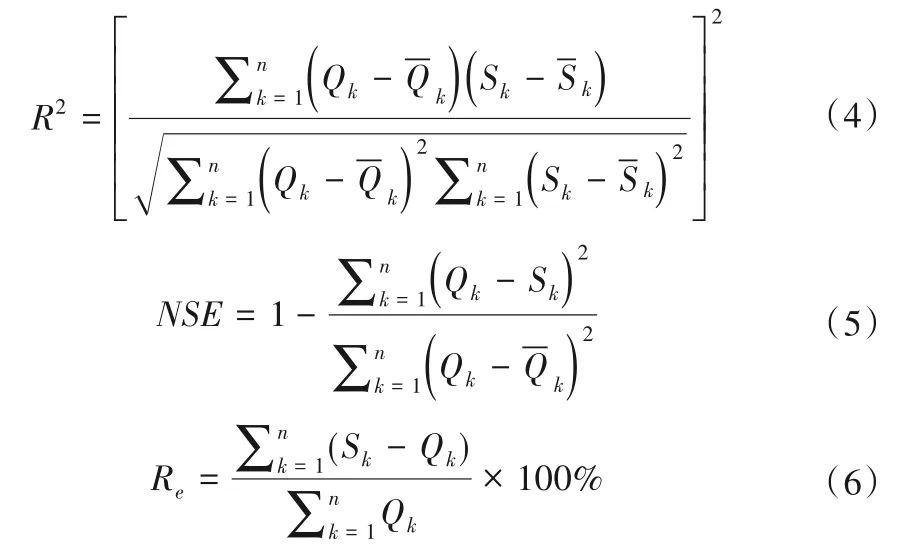
式中：Qk为第k个实测流量；Sk为第k个模拟流量为实测流量的均值为模拟流量的均值。

在参数敏感性分析的基础上，进行多次迭代，使模拟结果与实测结果较为拟合，此时月径流R2为0.92，NSE为0.90，Re为-9.1%。选取2013.1.1-2015.12.31 的实测流量数据作为验证资料，将参数组代入SWAT模型进行模拟验证，模拟结果与实测径流拟合较好，此时月径流R2为0.85，NSE为0.81，Re为8.6%，精度达到模型的良好标准，率定期和验证期的模拟结果如图6。

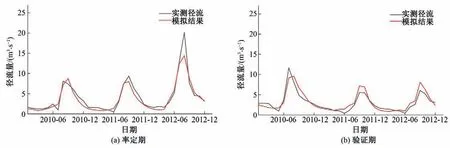
图6 阜平站实测月径流与模拟径流对比Fig.6 Comparison of measured monthly runoff and simulated runoff at Fuping Station

3 基于降水随机模拟的径流预测

3.1年际-年内降水统计分析

由图7 可得：1958-2017年间，阜平站年降水量在均值线附近上下波动，21世纪以来，年降水量的波动幅度逐渐趋于平缓。汛期降水量占全年降水量比重大多为80%～90%，且年降水量过大或过小时，汛期降水占比相比均值存在较大的偏差，即年降水量的量级和降水年内分布的规律存在一定的相关性。因此针对不同量级年降水量进行年内分布模拟更准确，根据多年降水量均值和均方差将年降水量划分为3 个状态，划分标准见表2。

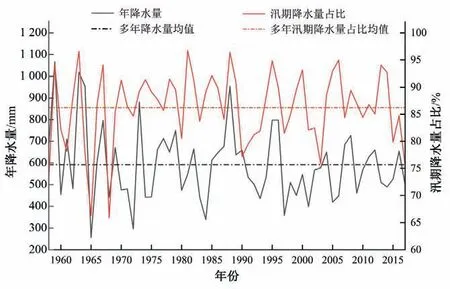
图7 1958-2017年阜平站年降水量Fig.7 Annual precipitation at Fuping Station from 1958 to 2017

为合理预测未来不同量级年降水量下的径流量，设置300 mm 为某一枯水年的年降水量，550 mm 为某一平水年的年降水量，800 mm 为某一丰水年的年降水量。根据状态I内22年的逐日降水量进行300 mm年降水量的年内分布模拟，同理根据状态II、状态III 内逐日降水量分别进行550、800 mm年降水量的年内分布模拟。

表2年降水量状态划分标准Tab.2 Standard for dividing annual precipitation status

3.2 降水随机模拟

根据阜平站1958-2017年的逐日降水数据，分别计算各状态下各月降水日的出现频率，结合式（1）、（2）估算降水状态转移概率，其中各月P（W/D）见图8。

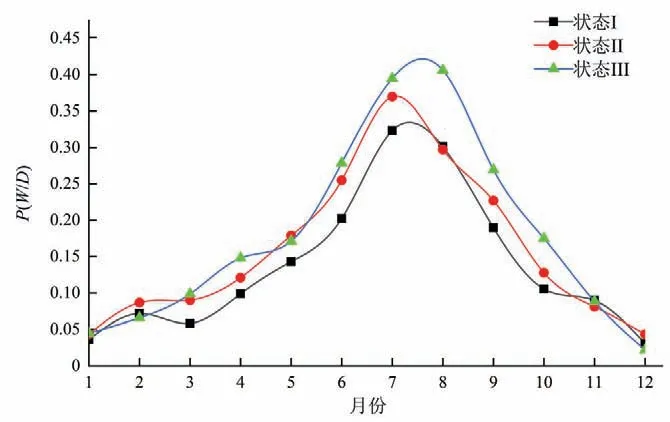
图8 各月降水状态转移概率P（W/D）Fig.8 Probability of monthly precipitation state transition P（W/D）

从图8 中可以看出P（W/D）总体上均呈现先增大后减小的趋势，且在汛期（5-9月）较大，在非汛期（10-4月）较小。当年降水量为状态III 时，P（W/D）最大值出现在8月；当年降水量为状态I 或II 时，P（W/D）最大值出现在7月。以各状态1月、7月、12月降水量为例，其Gamma 分布概率Q-Q 图见图9，同理可得不同状态年降水量的各月降水基本符合Gamma分布，满足构建耦合Markov 链-Gamma 分布随机模拟模型的要求，并计算相应的分布参数见图10。

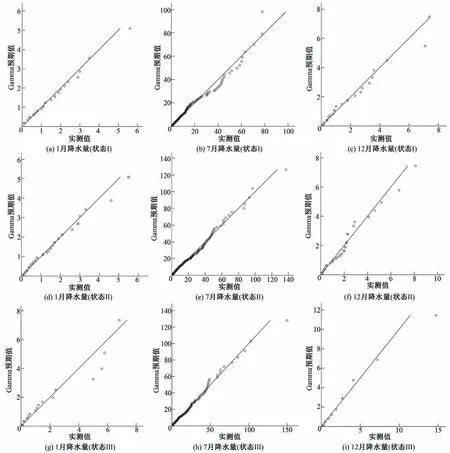
图9 各状态1、7、12月降水量Gamma分布Q-Q图Fig.9 Q-Q chart of Gamma distribution of precipitation in January，July and December under different states

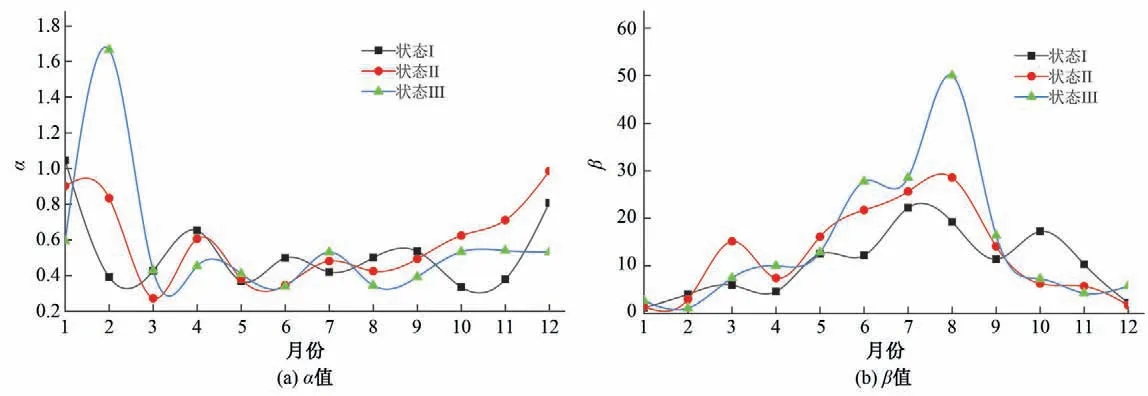
图10 不同状态年降水量各月Gamma分布参数Fig.10 Gamma distribution parameters of annual precipitation in different states

以800 mm年降水量的年内分布模拟为例，耦合状态III 中各月的降水转移概率和Gamma 分布参数，根据生成的随机数，连续进行100年的模拟，综合考虑年降水总量接近800 mm、汛期降水量占比和各月降水天数与样本均值相近等条件选取模拟年，对其进行适当修正后即可得800 mm年降水量在日尺度上的分配。同理，求得550 mm 和300 mm年降水量的年内分配见图11。

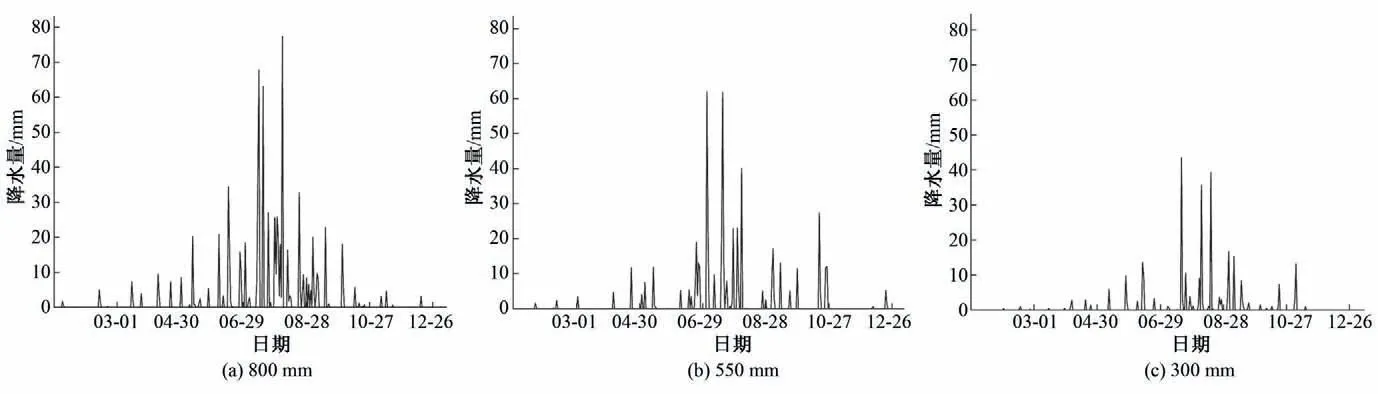
图11 不同量级年降水量年内分配Fig.11 Annual distribution of precipitation in different magnitudes

3.3 不同量级降水下的径流预测

将模拟的日降水输入到SWAT 模型中，结合已验证的参数进行输出，即可得出3种降水情景下的月径流过程线见图12。

由图12 可得，年降水量为800、550、300 mm 的随机降水模拟结果输出的阜平水文站月径流过程中，三者均呈现减小-增大-减小的变化趋势，且1 至3月的径流量基本相等，这是由于汛期降水量占了年降水量较大的比重，不同量级的年降水量在1 至3月份的降水分配相差不大；年降水量为800 mm 相对应的月径流过程中，月径流量在8月份达到最大，为17.81 m3/s，全年平均径流量为5.97 m3/s；年降水量为550 mm 相对应的月径流过程中，月径流量在9月份达到最大，为7.01 m3/s，全年平均径流量为2.79 m3/s；年降水量为300 mm 相对应的月径流过程中，月径流量在9月份达到最大，为4.08 m3/s，全年平均径流量为1.51 m3/s。

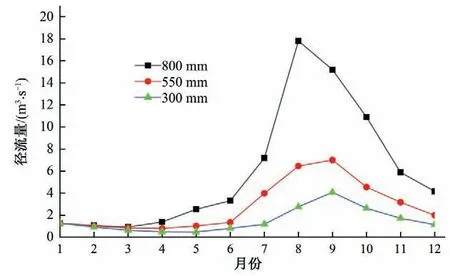
图12 不同量级年降水量下的径流模拟Fig.12 Runoff simulation under annual precipitation of different magnitudes

4 结 论

基于2015年土地利用数据构建相应的SWAT 模型，可得CN2、GW_DELAY、SOL_BD等参数对径流模拟结果的影响较为显著；根据流域内阜平水文站2008-2015年的实测径流数据对模型进行率定和验证，率定期和验证期的R2和NSE均高于0.8，|Re|均小于10%，表明该SWAT 模型对于研究区域径流的模拟结果良好。

根据阜平站1958-2017年逐日降水数据可得，不同降水量级对应的年内分布规律存在一定差异。在此基础上，分别构建了耦合Markov-Gamma 分布的降水随机模拟模型，并生成了年降水量为800、550、300 mm 对应的日降水过程，输入模型后得三种降水情景下的年径流量分别为5.97、2.79、1.51 m3/s，最大月径流量分别为17.81、7.01、4.08 m3/s。这一结论体现了不同量级降水对径流过程的影响，可为后续降雨-径流关系的研究提供理论基础。此外，耦合Markov-Gamma 分布的降水随机模拟模型没有充分考虑特大暴雨等极端降水事件，从而在一定程度上影响径流的模拟，因此对极端降水的发生过程进行研究并和降水模拟相结合是一个研究方向。