基于鲸鱼优化算法的区域水资源优化配置研究
田林钢,杨 丹
(华北水利水电大学,郑州450046)
1 研究背景
水资源是人类赖以生存的重要资源,在人类的生产生活中发挥着重要的作用,是国家可持续发展的基础[1-3]。随着社会的不断进步和经济的快速发展,水资源需求与供给的矛盾日趋严重,水资源短缺与水环境恶化等问题已经成为社会发展的制约因素[4-7]。为解决区域水资源短缺问题,通过水资源优化配置,对区域有限的、不同形式的水资源进行科学合理分配,实现水资源可持续利用和社会可持续发展。
目前国内水资源优化配置研究受到学术界的广泛关注,研究方法正逐步趋于成熟[8,9]。沙金霞等应用粒子群算法实现了引大济湟工程受水区在不同规划水平年下的水资源优化配置[10];曾萌等运用鱼群算法解决了广东省的水资源分配问题[11];潘俊等以沈阳市为实例分析,使用遗传算法对水资源量进行优化配置[12];刘玒玒等运用蚁群算法实现了黑河流域的水资源配置[13]。这些算法均在水资源优化配置中得到应用,但存在收敛速度较慢,易陷入局部最优等问题。鉴于此,本文将鲸鱼优化算法与水资源优化配置问题相结合,该算法具有收敛速度快、收敛精度高和全局寻优能力强等特点[14]。以河南省某县为例,以经济效益、社会效益和生态效益最优为目标,构建水资源优化配置模型,利用鲸鱼优化算法求解出该县不同规划年(2025年和2030年)的水资源优化配置方案,以期实现该区域水资源合理开发利用,使该区域的经济社会得到协调发展。
2 鲸鱼优化算法
鲸鱼被认为是世界上最大的哺乳动物,成年鲸鱼可以达到30 m 长,180 t 重。研究表明,鲸鱼大脑的特定区域内有着类似于人类的梭形细胞,这些细胞负责人类的判断、情感和社会行为。换言之,梭形细胞使鲸鱼区别于其他生物[15]。2016年,澳大利亚学者Seyedali Mirjalili 和Andrew Lewis 提出了一种新型群体智能优化算法——鲸鱼优化算法(Whale Optimization Algorithm,WOA)[16]。该算法受座头鲸捕食行为的启发,对座头鲸群体的收缩包围、螺旋式位置更新和随机捕猎机制进行模拟,其数学模型包括环绕式捕食、泡泡网捕食和搜索捕食3 个阶段。
2.1 环绕式捕食
在环绕式捕食中,座头鲸能识别猎物的位置并对其进行包围。假设当前最优位置为目标猎物位置,在定义了最优位置之后,其他鲸鱼个体会朝着最优位置不断更新它们的位置。其位置更新的表达式为:
式中:t为当前迭代次数和为系数向量为当前鲸群个体的最优位置为当前鲸群个体的位置。
的计算公式为:

2.2 泡泡网捕食
根据座头鲸的泡泡网捕食行为,建立如下两种机制的数学模型。
(1)收缩包围机制:该行为是通过减小参数来实现的。随着的减小而减小,即的取值范围是[-a,a]。当的取值范围在[-1,1]时,鲸鱼个体的新位置可以定义在当前鲸群个体位置和最优位置之间的任意位置。
(2)螺旋式位置更新机制:首先计算鲸鱼个体和猎物(当前最优位置)之间的距离,然后在鲸鱼个体和猎物(当前最优位置)的位置之间建立一个螺旋数学模型,以模拟座头鲸的螺旋形运动。其数学模型为:
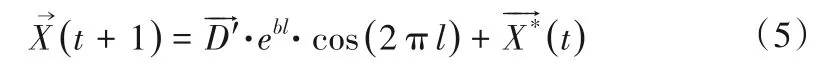
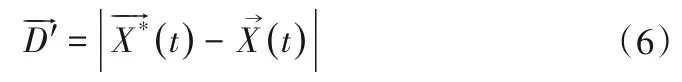
座头鲸在收缩包围猎物的同时,也沿着螺旋形路径运动。为了模拟这种行为,假设收缩包围机制和螺旋式位置更新机制的更新概率相同,均为50%。其数学模型为:
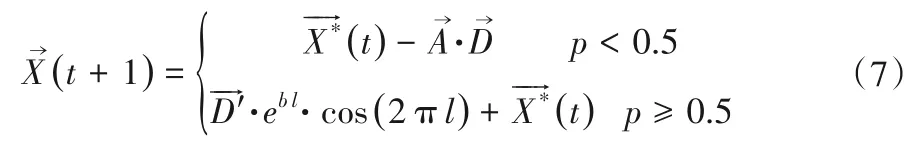
式中:p为[0,1]之间的随机数。
2.3 搜索捕食
搜索捕食是通过的大小来搜索猎物的。在搜索捕食过程中,鲸鱼个体会根据彼此的位置进行随机搜索猎物。因此,设定迫使鲸鱼个体远离猎物,搜索其他更合适的猎物。这种机制以增强算法的搜索捕食能力,使该算法能进行全局搜索。其数学模型如下:
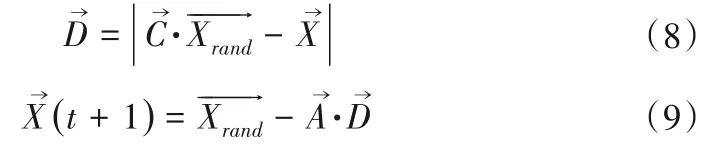
3 实例分析
3.1 研究区概况
某县位于河南省西北部,地势西高东低,自西向东倾斜,县域面积805 km2,属暖温带大陆型季风气候,年平均降雨量575.10 mm。由于该县经济在快速发展阶段,水资源的开发利用呈快速增长趋势,导致整个区域水资源量短缺,供需矛盾突出,以及经济发展与水资源协调不够等一系列水资源问题。因此,对该区域的水资源进行合理配置,实现不同水源和用水部门之间的供需水量平衡。
3.2 供需水量预测
该县供水水源主要包括地表水(沁河水、黄河水、南水北调水以及其他地表水)、地下水和再生水,不同水平年的可供水量预测结果见表1。
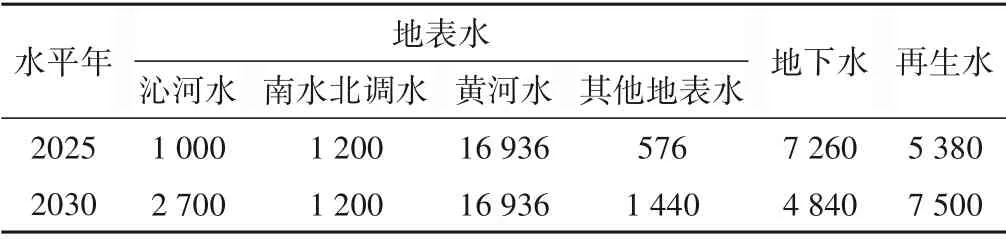
表1 不同水平年的供水量预测结果 万m3Tab.1 Prediction results of water supply in different level years
该县用水部门主要包括生活用水、农业用水、工业用水、第三产业用水和生态用水。以2017年为现状基准年,采用定额法预测2025年与2030年该县各用水部门的需水量,具体结果见表2。
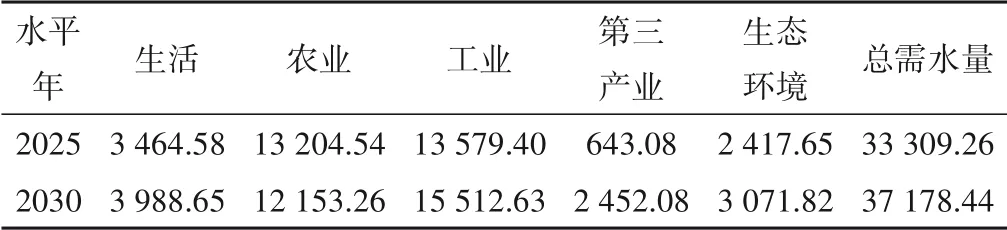
表2 不同水平年的需水量预测结果 万m3Tab.2 Prediction results of water demand in different level years
3.3 水资源优化配置模型
3.3.1 目标函数
(1)经济效益目标。以区域供水经济效益最大来表示:
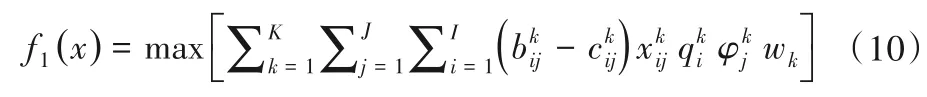
(2)社会效益目标。以区域总缺水量最小来表示:
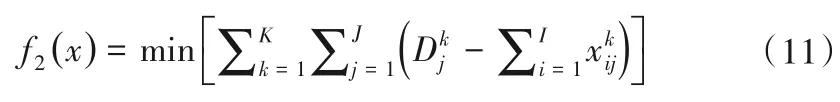
(3)生态效益目标。以区域重要污染物化学需氧量(COD)排放总量最小来表示:
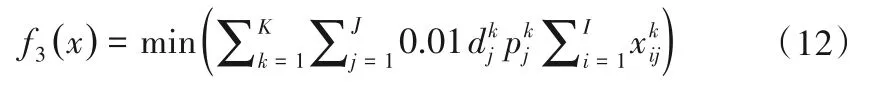
3.3.2 约束条件
(1)供水能力约束。k子区i水源向所有用户的供水总量应不大于其可供水量:

(2)需水能力约束。水源向用户所分配的水量应介于用户需水量上下限之间:
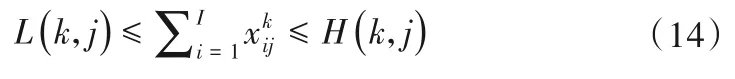
式中:L(k,j)、H(k,j)分别为k子区j用户需水量的上限、下限。
(3)废水污染物质量浓度约束。k子区j用户排放的废水中重要污染物(COD)的浓度应在国家允许的排放指标内,且排放的重要污染物总量应不超过该区域的最大允许排放量:
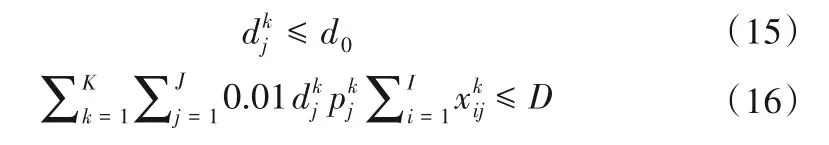
式中:d0表示在各行业中国家标准规定所排放的重要污染物(COD)质量浓度,mg/L;D表示区域内最大允许排放重要污染物的总量。
(4)变量非负约束。

3.3.3 模型参数确定
(1)权重确定。采用层次分析法和熵权法组合赋权,确定经济、社会和生态环境3 个效益目标权重,分别为0.47、0.30、0.23。
(2)供水效益系数。基于居民生活用水优先序最高的原则,结合某县及周围地区的实际情况,生活供水效益系数取0.05 万元/m3。2025年农业供水效益系数0.002 6 万元/m3,工业供水效益系数取0.018 2 万元/m3,第三产业供水效益系数取0.200 0 万元/m3;2030年农业供水效益系数0.004 5 万元/m3,工业供水效益系数取0.025 0 万元/m3,第三产业供水效益系数取0.153 8 万元/m3。由于城市生态环境与居民生活密切相关,故取生态供水效益系数等于生活供水效益系数,取0.05 万元/m3。
(3)供水费用系数。费用系数参考该县水价及税费征收标准,确定生活用水费用系数2.35 元/m3、农业用水费用系数0.40元/m3、工业用水费用系数2.90 元/m3、第三产业用水费用系数3.60 元/m3、生态用水费用系数2.35 元/m3。
(4)供水次序系数。供水次序系数反映k子区i水源相比于其他水资源优先使用程度的一种度量。水源供水次序系数参考下式确定[17]:
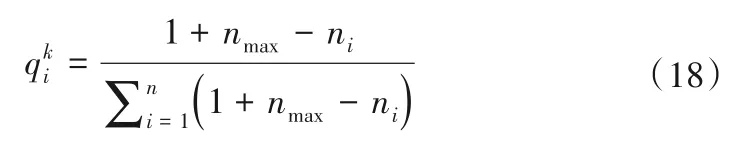
式中:ni为i水源供水次序序号;nmax为最大水源供水序号。
基于某县各供水水源的实际情况及各用水部门用水的重要程度,确定某县水源的供水次序为:其他地表水、沁河水、南水北调水、黄河水、地下水、再生水。由上式确定各水源供水次序系数分别为:0.29、0.24、0.19、0.14、0.10、0.05。
(5)用水公平系数。参考某县各用水部门的重要程度,得到各用水部门的先后次序为:生活用水、生态用水、工业用水、第三产业用水和农业用水。参照供水次序系数的计算公式,计算得到各用户的用水公平系数分别为0.33、0.27、0.20、0.13、0.07。
(6)鲸鱼优化算法参数设置。鲸鱼种群数目N=150,最大迭代次数tmax=900。
3.3.4 模型求解过程
在建立以经济、社会和生态效益为目标函数的水资源优化配置模型和确定相关参数后,利用鲸鱼优化算法对模型进行求解,具体求解步骤如下:
(1)随机产生N只鲸鱼作为初始种群,初始化算法参数和最大迭代次数tmax。
(2)以河南省某县为例,根据经济、社会和生态环境3 个目标函数确定的权重,将多目标问题转换为单目标问题,然后计算每只鲸鱼个体的适应度值,找到当前适应度值最佳的鲸鱼个体。
(3)进入算法主循环过程,当p<0.5 时,若利用公式(1)和(2)更新当前鲸鱼个体位置;若利用公式(8)和(9)更新鲸鱼个体位置。当p≥0.5 时,利用公式(5)和(6)更新鲸鱼个体位置。
(4)计算更新后每只鲸鱼个体的适应度值,找到全局最优的鲸鱼个体。
(5)判断算法是否满足终止条件,若满足,则输出最优鲸鱼个体的位置及其对应的适应度值;否则,令t=t+1,转到步骤(3)继续进行算法迭代。
3.4 结果与分析
通过结合某县的实际情况,以及水资源优化配置模型的相关参数,利用Matlab 软件求解出该县不同水平年的水资源优化配置结果。具体计算结果和供需平衡关系见表3和表4。
(1)配水量分析。分析表3和表4可以看出,2025年某县各用水部门按配水比例依次排序为工业、农业、生活、生态、第三产业,该顺序与2025年某县各用水部门预测需水量的结果一致。2030年各用水部门排序结果与2025年相同,符合该县地区的实际情况。从配水比例看,2030年相比于2025年,农业配水有所减少,生活、生态、工业和第三产业配水增加,该结果符合需水预测结果。
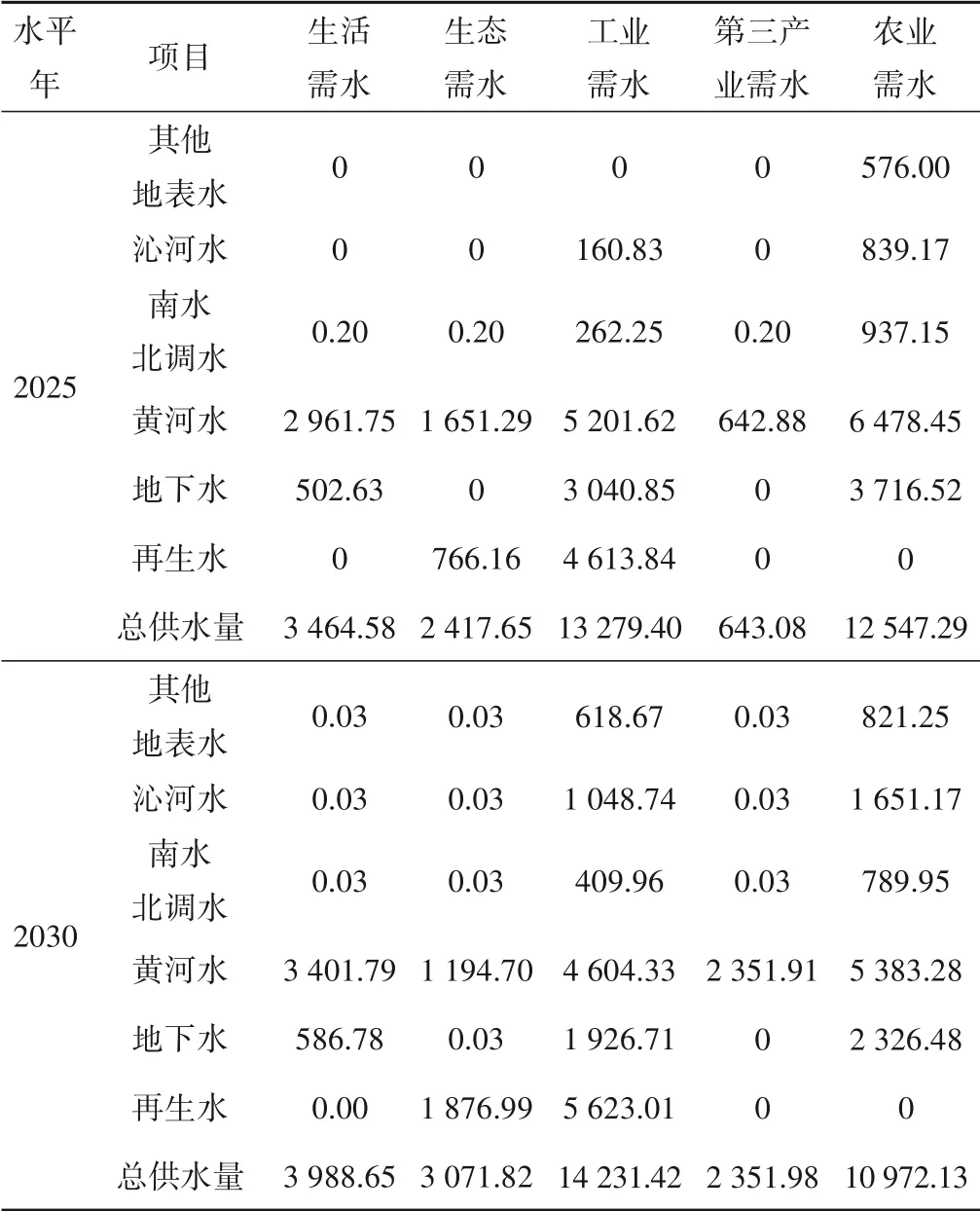
表3 不同水平年的水资源优化配置结果 万m3Tab.3 Results of water resources optimization in different level years
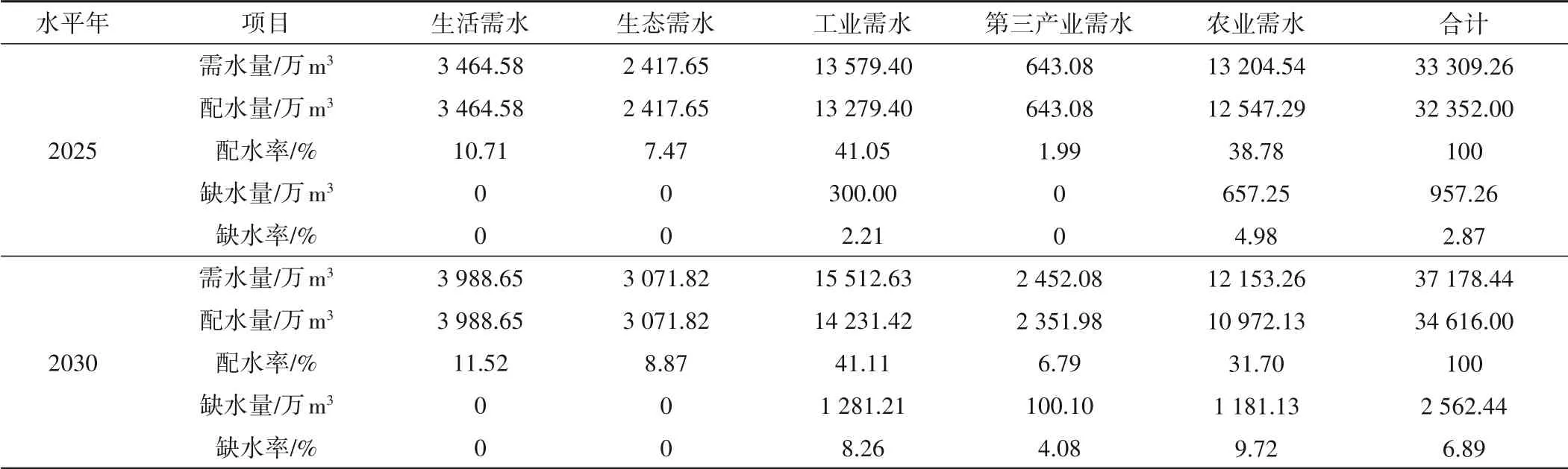
表4 不同水平年的供需平衡关系表Tab.4 Balance of supply and demand in different level years
(2)缺水量分析。将某县水资源优化配置结果和需水量预测结果进行对比,可知该配置方案充分满足生活需水、生态需水,允许生产部门少量缺水,符合可持续发展原则与用户用水公平原则。该地区的缺水情况主要集中于生产部门,在生产用水部门配水中,综合考虑经济、社会和生态效益,尽量保证工业与第三产业生产用水的基本需求,允许少量缺水,但由于农业部门用水公平系数较低,相较于其他两个生产部门出现缺水情况较为严重。总体来看,在经济、社会和生态环境综合效益最大的前提下,该区域不同水平年的缺水率都控制在10%以内,表明建立的水资源优化配置模型和设置的参数是合理的。
4 结 语
本文以经济、社会和生态环境目标函数及相应的约束条件建立河南省某县的水资源优化配置模型,并运用鲸鱼优化算法对模型进行了求解。研究结果表明2025年和2030年该县的水资源量可充分满足生活需水和生态需水,只在生产用水部门存在少量缺水,缺水率在10%以内,基本满足未来用水需求,配置方案科学合理,可为该县未来的水资源规划和管理提供科学合理的依据。运用的鲸鱼优化算法克服了传统优化算法收敛速度慢等问题,在求解水资源优化配置问题上表现出较好的适应性和有效性,在水资源优化配置方面具有良好的应用前景。

