一类Pell方程组的非负整数解*

王志兰

(1.泰州学院 数理学院,江苏 泰州 225300;2.江苏省吴江中等专业学校,江苏 吴江 215200)

1 引言及主要结论

x2-dy2=1与y2-Dz2=4,x,y,z∈,

(1)

的求解一直是热门话题.目前的结论主要有：

(i)d=2,D≢-1(mod 12)且D为不超过6个不同的奇素数之积以及D≡-1(mod 12)且D为不超过3个不同的奇素数之积时，陈永高[1]分别证明了除D为3×5×7×11×17×577，17×19×29×41×59×577外，(1)仅有平凡解z=0，以及除D为5×7，29×41×239外，(1)仅有平凡解z=0.

(ii)d=2,D=2p1…ps(p1,…,ps为不同的奇素数, 1≤s≤6)时，管训贵[2]证明了除D为2×17，2×3×5×7×11×17以及2×17×113×239×337×577×665857外，(1)仅有平凡解z=0.

(iii)d=2,D为偶数且D没有适合p≡1(mod 8)的素因子p时，乐茂华[3]证明了(1)仅有平凡解z=0.

(iv)d=6,D=p为奇素数时，苏小燕[4]证明了除D=11外，(1)仅有平凡解z=0.

(v)d=6,D=2p1…ps(p1,…,ps是不同的奇素数, 1≤s≤4)时，杜先存等[5]证明了除D为2×11×97外，(1)仅有平凡解z=0.

本文进一步讨论d=s(s+1)，D=2q1或2q1q2(q1,q2为不同的奇素数)时方程(1)的求解问题,得出以下一般性的结果.

定理1设p,q1,q2为不同的奇素数，且p=2s+1，s≡2(mod 4)，D=2c(c∈N*，c=q1或q1q2)，则Pell方程组

(2)

除平凡解(X,Y,Z)=(2s+1,2,0)外，当2p2-1=cr2(r∈N*)时，(2)仅有解(X,Y,Z)=(4p3-3p,8p2-2,4pr).

2 引理

引理1设D∈N*且不是平方数，则Pell方程

x2-Dy2=1，x,y∈N*,

(3)

证明参见文[6，定理6.11].

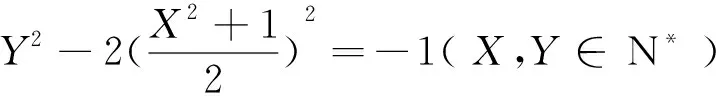
证明参见文[7].

引理3不定方程

2Y2=X4-4X2+2，X,Y∈N,

仅有解(X,Y)=(2,1)和(0,1).

证明参见文[8].

引理4若D是一个非平方的正整数,则不定方程x4-Dy2=1(x,y∈N*)除当D=1785，4·1785，16·1785时，分别有两组解(x,y)=(13,4)，(239,1352)；(x,y)=(13,2)，(239,676)；(x,y)=(13,1)，(239,338)外，至多只有一组解(x1,y1)，且满足

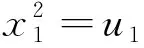
证明参见文[9].

引理5若D是一个非平方的正整数,则不定方程

x2-Dy4=1，x,y∈N*,

证明参见文[10].

由引理5立得

引理6设p为奇素数，则不定方程x2-(p2-1)y4=1(x,y∈N*)仅有解(x,y)=(p,1).

3 定理1的证明

因D≡2(mod 4)，故由(2)的第二式知，Y,Z均为偶数. 令X=x，Y=2y，Z=2z，则(2)成为

(4)

容易验证下列各式成立：

xk+2=2pxk+1-xk，x0=1，x1=p，x2=2p2-1；

(5)

yk+2=2pyk+1-yk，y0=0，y1=1，y2=2p；

(6)

xk+l=xkxl+(p2-1)ykyl，yk+l=xkyl+xlyk；

(7)

x-k=xk，y-k=-yk；

(8)

(9)

若(x,y,z)=(xk,yk,z)是(4)的解，则根据k的奇偶性分以下两种情形讨论.

情形1当2|k时，可令k=2l(l∈N*).由(4)的第一式知

(10)

将式(10)代入(4)的第二式，并结合式(9)得

(11)

因为

故式(11)可改写成

(12)

又

因而

令D=b1b2，gcd(b1,b2)=1,则式(12)可化为

(13)

或

(14)

若式(13)成立，则由(13)的第二式得

(15)

由gcd(s,p)=gcd(s,2s+1)=1知，式(15)成为

(16)

根据式(5)，当2|l时，xl≡±1(mod 2s+1)；当2⫮l时，xl≡0(mod 2s+1).故由式(16)得-s,-s-1≡0(mod 2s+1)，显然不可能.因此式(13)不成立.

若式(14)成立，则由(14)的前两式得

(17)

易知，Legendre符号(注意:p≡1(mod 4))

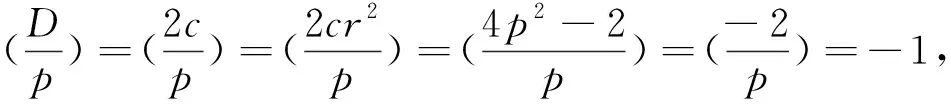
情形2当2⫮k时，可令k=2l-1(l∈N*).由(4)的第二式知

(y2l-1+1)(y2l-1-1)=Dz2.

(18)

再由(7)、(8)两式可得

y2l-1+1=2xl-1yl，y2l-1-1=2xlyl-1.

(19)

根据式(6)，gcd(y2l-1+1,y2l-1-1)=2，故gcd(xl-1yl,xlyl-1)=1.

将式(19)代入式(18)，整理得

Dz2=4xl-1yl-1xlyl.

(20)

若l=1，则式(20)成为Dz2=4x0y0x1y1=0,此时z=0，可得(4)的平凡解(x,y,z)=(p,1,0),从而可得(2)的平凡解(X,Y,Z)=(2s+1,2,0).

若l=2，则式(20)成为Dz2=4x1y1x2y2=8p2(2p2-1)，即cz2=4p2(2p2-1).考虑到gcd(4p2,2p2-1)=1，当2p2-1=cr2(c,r∈N*，c=q1或q1q2，q1,q2为不同的奇素数)时，z=2pr,可得(4)的一组解为(x,y,z)=(4p3-3p,4p2-1,2pr),从而可得(2)的一组解为(X,Y,Z)=(4p3-3p,8p2-2,4pr).

若l=3，则式(20)成为

Dz2=4x2y2x3y3=8p2(2p2-1)(2p-1)(2p+1)(4p2-3).

(21)

这里2p2-1,2p-1,2p+1,4p2-3两两互素.

由于p≡1(mod 4)，即2p+1≡3(mod 8)，故2p+1非平方数.

当4p2-3=w2(w∈N*)时，p=1，不合题意，故4p2-3也非平方数.

当2p2-1=u2，2p-1=v2(u,v∈N*)时，有

(22)

根据引理2，式(22)给出v=1或3，故p=1(不合题意)，或p=5.因此当p≠5时，式(21)右边至少提供4个不同的非平方素因子(其中包括2)，而左边至多提供3个不同的非平方素因子(其中包括2)，矛盾；另外，当p=5时，由2×52-1=cr2得c=1，与c=q1或q1q2矛盾.

若l=4，则式(20)成为

Dz2=4x3y3x4y4=16p2(4p2-3)(2p+1)(2p-1)(2p2-1)(8p4-8p2+1).

(23)

这里4p2-3,2p+1,2p-1,2p2-1,8p4-8p2+1两两互素.

当8p4-8p2+1=t2(t∈N*)时，有

2t2=(2p)4-4(2p)2+2.

(24)

根据引理3，式(24)给出2p=2或0,显然不可能.故式(23)右边至少提供4个不同的非平方素因子，仍得矛盾.

下面讨论l≥5的情形.

(i) 考虑到gcd(xl-1,yl-1)=gcd(xl,yl)=gcd(xl-1,xl)=gcd(yl-1,yl)=1，且由(7)、(8)两式知

gcd(xl,yl-1)=gcd(pxl-1+(p2-1)yl-1,yl-1)=gcd(pxl-1,yl-1)=gcd(p,yl-1)=1或p,

gcd(xl-1,yl)=gcd(xl-1,xl-1+pyl-1)=gcd(xl-1,pyl-1)=gcd(xl-1,p)=1或p,

故当gcd(xl,yl-1)=p时，gcd(xl-1,yl)=1；当gcd(xl-1,yl)=p时，gcd(xl,yl-1)=1.

(ii) 若xl-1=A2(A∈N*)，则(2)的第一式成为

(25)

因为p2-1≠1785，4·1785，16·1785，所以根据引理4，方程(25)至多只有一组解满足A2=p或2p2-1，即xl-1=p或2p2-1，因此l=2或3，不符合要求，故xl-1≠A2.

(iii) 若xl=A2(A∈N*)，则由(ii)的讨论知l=3或4，也不符合要求，故xl≠A2.

(iv) 若yl-1=B2(B∈N*)，则(2)的第一式成为

(26)

根据引理6，式(26)给出xl-1=p，此时l=2，不符合要求， 故yl-1≠B2.

(v) 若yl=B2(B∈N*)，则由(iv)的讨论知l=3，也不符合要求，故yl≠B2.

综合(i)～(v)知，若l≥5，则式(20)右边至少提供4个不同的非平方素因子，与题设矛盾.定理得证.