有界简单格的不可比图的亏格*
罗士峰,邓贵新,黄春红
(南宁师范大学 数学与统计学院,广西 南宁 530100)
1 引言
格是一类重要的代数结构.孙中举和方捷引入了有限格的正则图[1];Javaheri引入了格的余极大图,并研究了其线图的亏格问题[2];Wasadikar和Survase定义了格的不可比图,并研究了它的围长、零因子和单位的性质[3,4].本文研究格的不可比图的亏格.使一个图G嵌入到拓扑平面Sk中的最小自然数k称为G的亏格,记作γ(G).特别地,平面图的亏格为0.
定义1.1设E是偏序集,a,b∈E,若a≤b或b≤a,则称a与b是可比的.若E中任何两个元素都可比,则称E是一个链.若链E含有n+2个元素,则称E的长度为n.
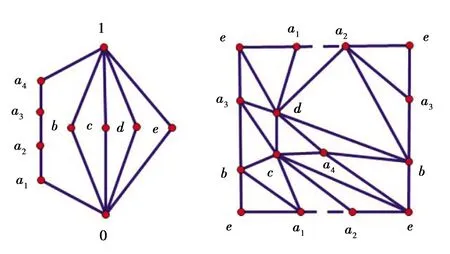
定义1.2设E是偏序集,m∈E,若对任意a∈E都有m≤a,则称m为E的最小元,记为0.对偶地可定义E的最大元,记为1.若E中元素a满足a≠0,且不存在b∈E使得0 定义1.3设L是偏序集,若L中任何两个元素在L中都有上、下确界,则称L是一个格.如果L有最大元1和最小元0,则称L是有界的;若L中除0,1外的任一元素都只有两个元素与之相邻,则称L是简单格. 定义1.4设L是格,L的不可比图记作Γ(L),它以L{0,1}为顶点集,两个顶点a与b相连当且仅当a与b不可比. 本文中出现的其他的图论和格论术语可参见[5,6]. 以下所讨论的格均为有限格.易知一个有界简单格L由它所含的链数k及各条链的长度c1,c2,…,ck决定(不妨设c1≥c2≥…≥ck≥1),故可记L为(c1,c2,…,ck),此时L含有k个原子,于是Γ(L)含有子图Kk.特别地,当k=1时L=c1是一条链,此时Γ(L)为空图.故以下均设k≥2. 本节给出一些引理,均是为下一节主要结果的证明作准备. 引理2.1设m,n,p均为正整数. 引理2.2[7]设简单连通图G有v个顶点和e条边. 引理2.3[10]若简单图G含有9个顶点和33条边,则γ(G)=3. 引理2.4[11]γ(K2,2,2,2,1)=3. 引理2.5[9]γ(K4,2,2,2)=3. 引理2.6γ(K3,3,3,1)=3. 证明因K3,3,3,1含有10个顶点和36条边,故由引理2.2知γ(K3,3,3,1)≥2,注意到K3,3,3,1在S2上是不存在三角嵌入的,因而其亏格为3. 设有界简单格L=(c1,c2,…,ck).若k≥9,则γ(Γ(L))≥γ(K9)=3,故当γ(Γ(L))≤2时必有k≤8.同理可知,当k≥8时γ(Γ(L))≥2,当k≥5时γ(Γ(L))≥1. 定理3.1设L=(c1,c2),则 (1)γ(Γ(L))=0当且仅当c2≤2; (2)γ(Γ(L))=1当且仅当(c1,c2)=(3,3),(4,3),(5,3),(6,3),(4,4); (3)γ(Γ(L))=2当且仅当(c1,c2)=(7,3),(8,3),(9,3),(10,3),(5,4),(6,4). 证明此时Γ(L)=Kc1,c2,由引理2.1(2)即得结论. 定理3.2设L=(c1,c2,…,c8),则γ(Γ(L))=2当且仅当(c1,c2,…,c8)=(1,1,1,1,1,1,1,1). 定理3.3设L=(c1,c2,…,c7),则 (1)γ(Γ(L))=1当且仅当(c1,c2,…,c7)=(1,1,1,1,1,1,1); (2)γ(Γ(L))=2当且仅当(c1,c2,…,c7)=(2,1,1,1,1,1,1). 证明如果c1≥3,则Γ(L)含有子图K3,1,1,1,1,1,1,注意到该子图是含有9个顶点和33条边的简单图,由引理2.3知其亏格为3,因此γ(Γ(L))≥3. 若c1=1,则Γ(L)=K7,故γ(Γ(L))=γ(K7)=1. 定理3.4设L=(c1,c2,…,c6),则 (1)γ(Γ(L))=1当且仅当(c1,c2,…,c6)=(1,1,1,1,1,1)或(2,1,1,1,1,1); (2)γ(Γ(L))=2当且仅当(c1,c2,…,c6)=(3,1,1,1,1,1),(4,1,1,1,1,1)或(2,2,1,1,1,1). 证明若c3≥2,则c1≥c2≥2,于是Γ(L)含有子图K2,2,2,1,1,1,而K2,2,2,1,1,1又含有子图K2,2,2,2,1,故由引理2.4知γ(Γ(L))≥3.因此我们只需考虑c3=1的情形. 图1格L=(3,2,2,1,1)及Γ(L)=K3,2,2,1,1在S2中的嵌入 接着考虑c2=1的情况. 若c1≥5,则Γ(L)含有子图K5,1,1,1,1,1,而K5,5是K5,1,1,1,1,1的子图,因此γ(Γ(L))≥γ(K5,1,1,1,1,1)≥γ(K5,5)≥3. 若c1=4,则由引理2.2知γ(Γ(L))≥2,又注意到Γ(L)可嵌入S2(如图2所示),故其亏格为2. 图2格L=(4,1,1,1,1,1)及Γ(L)=K4,1,1,1,1,1在S2中的嵌入 若c1=2,则Γ(L)=K2,1,1,1,1,1⊆K7,所以γ(Γ(L))=1. 若c1=1,则Γ(L)即为K6,故其亏格为1. 定理3.5设L=(c1,c2,…,c5),则 (1)γ(Γ(L))=1当且仅当(c1,c2,c3,c4,c5)=(1,1,1,1,1),(2,1,1,1,1),(3,1,1,1,1),(4,1,1,1,1),(2,2,1,1,1),(3,2,1,1,1); (2)γ(Γ(L))=2当且仅当(c1,c2,c3,c4,c5)=(5,1,1,1,1),(6,1,1,1,1),(4,2,1,1,1),(3,3,1,1,1),(2,2,2,1,1),(3,2,2,1,1). 证明如果c4≥2,则c1≥c2≥c3≥2,此时Γ(L)含K2,2,2,2,1作为子图,而由引理2.4知γ(K2,2,2,2,1)=3,所以γ(Γ(L))≥3.故c4=c5=1. 若c3≥3,则c1≥c2≥3,此时Γ(L)含K3,3,3,1,1作为子图,而K6,5⊆K3,3,3,1,1,所以γ(Γ(L))≥γ(K6,5)=3.因此c3≤2. 当c3=2时,若c2≥3,则K3,3,2,1,1⊆Γ(L),但K5,5⊆K3,3,2,1,1,所以γ(Γ(L))≥γ(K5,5)=3,故c2=2.若c1≥4,则K5,5⊆K4,2,2,1,1⊆Γ(L),进而有γ(Γ(L))≥γ(K5,5)=3. 最后考虑c3=1的情况. 若c2≥4,则K6,5⊆K4,4,1,1,1⊆Γ(L),而若c2=3且c1≥4,则有K5,5⊆K4,3,1,1,1⊆Γ(L),于是都有γ(Γ(L))≥3,而图3给出了K3,3,1,1,1在S2上的嵌入,所以γ(K3,3,1,1,1)=2.当c2=3时,c1=3. 图3格L=(3,3,1,1,1)及Γ(L)=K3,3,1,1,1在S2中的嵌入 图4格L=(3,2,1,1,1)及Γ(L)=K3,2,1,1,1在S1中的嵌入 图5格L=(4,1,1,1,1)及Γ(L)=K4,1,1,1,1在S1中的嵌入 图6格L=(6,1,1,1,1)及Γ(L)=K6,1,1,1,1在S2中的嵌入 定理3.6设L=(c1,c2,c3,c4),则 (1)γ(Γ(L))=0当且仅当(c1,c2,c3,c4)=(1,1,1,1),(2,1,1,1); (2)γ(Γ(L))=1当且仅当(c1,c2,c3,c4)=(c1,1,1,1)(其中3≤c1≤6),(2,2,1,1),(3,2,1,1),(4,2,1,1),(3,3,1,1),(2,2,2,1),(2,2,2,1),(3,2,2,1),(2,2,2,2); (3)γ(Γ(L))=2当且仅当(c1,c2,c3,c4)=(c1,1,1,1)(其中7≤c1≤10),(5,2,1,1),(6,2,1,1),(4,3,1,1),(4,2,2,1),(3,3,2,1),(3,2,2,2). 证明若c4≥3,则K6,6⊆K3,3,3,3⊆Γ(L),这使得γ(Γ(L))≥γ(K6,6)≥3,故c4≤2. 接下来考虑c4=1的情形. 由引理2.6知c3≤2,否则Γ(L)含K3,3,3,1作为子图,使得γ(Γ(L))≥3. 情形1c3=2. 若c2≥4,则有K6,5⊆K4,4,2,1⊆Γ(L),进而γ(Γ(L))≥3. 若c2=3,则c1=3,否则K5,5⊆K4,3,2,1⊆Γ(L),从而γ(Γ(L))≥3.而c1=3,此时Γ(L)=K3,3,2,1.由于K5,4⊆K3,3,2,1⊆K3,3,1,1,1,因此γ(K3,3,2,1)=2. 若c2=2,则c1≤4,否则γ(Γ(L))≥γ(K5,2,2,1)≥γ(K5,5)=3.又因为K3,3⊆K2,2,1,1⊆K3,2,1,1⊆K3,1,1,1,1,故γ(K2,2,2,1)=γ(K3,2,2,1)=1. 情形2c3=1. 显然c2≥4是不成立的,因为K5,5⊆K4,4,1,1⊆Γ(L),这使得γ(Γ(L))≥3,故c2≤3. 当c2=3时c1∈{3,4},否则K5,5⊆K5,3,1,1⊆Γ(L),即γ(Γ(L))≥γ(K5,5)≥3,所以c1=3或4.一方面由于K4,4⊆K3,3,1,1,而K5,4⊆K4,3,1,1,另一方面因为K3,3,1,1⊆K3,2,1,1,1,K4,3,1,1⊆K4,2,1,1,1,所以γ(K3,3,1,1)=1,γ(K4,3,1,1)=2. 当c2=2时,易知c1≥7是不成立的,因为K7,4⊆K7,2,1,1⊆Γ(L),这使得γ(Γ(L))≥3.故2≤c1≤6.再因为K3,3⊆K2,2,1,1⊆K3,2,1,1⊆K3,1,1,1,1,K4,4⊆K4,2,1,1⊆K4,1,1,1,1,K5,4⊆K5,2,1,1⊆K6,2,1,1⊆K6,1,1,1,1,因此γ(K2,2,1,1)=γ(K3,2,1,1)=γ(K4,2,1,1)=1,γ(K5,2,1,1)=γ(K6,2,1,1)=2. 当c2=1时,若c1≥11,则K11,3⊆K11,1,1,1⊆Γ(L),导致γ(Γ(L))≥3,故c1≤10.若1≤c1≤2,则Γ(L)是平面图,即γ(Γ(L))=0.若3≤c1≤6,则Γ(L)=Kc1,1,1,故有K3,3⊆K3,1,1,1⊆K4,1,1,1⊆K5,1,1,1⊆K6,1,1,1,且图7给出K6,1,1,1在S1上的嵌入,故γ(Γ(L))=1.同理,若7≤c1≤10,则K7,3⊆K7,1,1,1⊆K8,1,1,1⊆K9,1,1,1⊆K10,1,1,1,且图8给出K10,1,1,1在S2上的嵌入,故γ(Γ(L))=2. 图7格L=(6,1,1,1)及Γ(L)=K6,1,1,1在S1中的嵌入 图8格L=(10,1,1,1)及Γ(L)=K10,1,1,1在S2中的嵌入 定理3.7设L=(c1,c2,c3),则 (1)γ(Γ(L))=0当且仅当(c1,c2,c3)=(c1,1,1),(2,1,1),(2,2,2),c1≥1; (2)γ(Γ(L))=1当且仅当(c1,c2,c3)=(3,2,1),(4,2,1),(5,2,1),(6,2,1),(3,3,1),(4,3,1),(3,2,2),(4,2,2),(3,3,2),(3,3,3); (3)γ(Γ(L))=2当且仅当(c1,c2,c3)=(7,2,1),(8,2,1),(9,2,1),(10,2,1),(5,3,1),(6,3,1),(4,4,1),(5,2,2),(6,2,2),(4,3,2),(4,4,2),(4,4,3). 证明若c1≥c2≥c3≥4,则有K8,4⊆K4,4,4⊆Γ(L),从而γ(Γ(L))≥γ(K4,4,4)≥γ(K8,4)=3,故c3≤3. 情形1c3=3.若c2≥4,则K7,4⊆K4,4,3⊆Γ(L),即γ(Γ(L))≥3.因此c2≤3.此时令c2=3,则当c1≥5时有K6,5⊆K5,3,3⊆Γ(L),这使得γ(Γ(L))≥3.故c1∈{3,4},于是由引理2.1(4)知γ(K3,3,3)=1,γ(K4,3,3)=2. 情形2c3=2.显然c2≤4.否则K7,5⊆K5,5,2⊆Γ(L),导致γ(Γ(L))≥3. 情形2.1c2=4.若c1≥5,则有γ(Γ(L))≥γ(K5,4,2)≥γ(K6,5)=3.而由引理2.1(4)知γ(K4,4,2)=2. 情形2.2c2=3.若c1≥5,则K5,5⊆K5,3,2⊆Γ(L),故有γ(Γ(L))≥3,所以c1≤4.再由引理1(4)知γ(K4,3,2)=2,γ(K3,3,2)=1. 情形2.3c2=2.若c1≥7,则γ(Γ(L))≥3,故c1≤6.由引理2.1(4)可得γ(K2,2,2)=0,γ(K3,2,2)=γ(K4,2,2)=1,γ(K5,2,2)=γ(K6,2,2)=2. 情形3c3=1.易知c2≥5时,K6,5⊆K5,5,1⊆Γ(L),从而γ(Γ(L))≥3,故c2≤4. 情形3.1c2=4.若c1≥5,则K5,4,1⊆Γ(L),即γ(Γ(L))≥3,因此c1=4.由引理2.1(4)知γ(K4,4,1)=2. 情形3.2c2=3.如果c1≥7,则K7,4⊆K7,3,1⊆Γ(L),导致γ(Γ(L))≥3.所以c1≤6.若c1≤5,则由引理2.1(4)可知γ(K5,3,1)=2,γ(K4,3,1)=γ(K3,3,1)=1.而若c1=6,则K6,4⊆K6,3,1⊆K6,1,1,1,1,且γ(K6,1,1,1,1)=2,因此γ(K6,3,1)=2. 情形3.3c2=2.显然c1≥11是不可能的,否则K11,3⊆K11,2,1⊆Γ(L),从而γ(Γ(L))≥3,故c1≤10.若c1≤5,则由引理2.1(4)可知γ(K5,2,1)=γ(K4,2,1)=γ(K3,2,1)=1,γ(K2,2,1)=0.而若c1=6,则Γ(L)=K6,2,1,且K6,3⊆K6,2,1⊆K6,1,1,1,故γ(Γ(L))=1.又因为K7,3⊆K7,2,1,故γ(K7,2,1)≥2.另一方面,因为K7,2,1⊆K8,2,1⊆K9,2,1⊆K10,2,1⊆K10,1,1,1,故γ(K7,2,1)=γ(K8,2,1)=γ(K9,2,1)=γ(K10,2,1)=2. 情形3.4c2=1.此时Γ(L)=Km,1,1显然是平面图,从而γ(Γ(L))=0. 本文确定了亏格小于3的有界简单格的结构.接下来我们将继续研究一般格的亏格问题,同时也将研究关于格的不可比图的其他问题,如正则性、团数的计算等.2 相关引理







3 主要结果
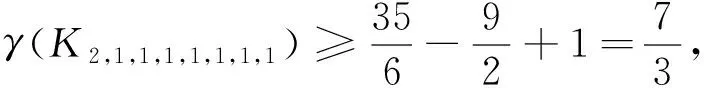
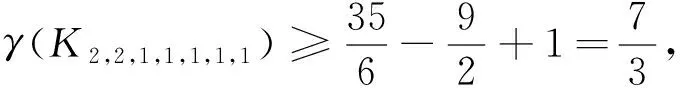
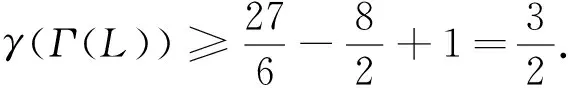





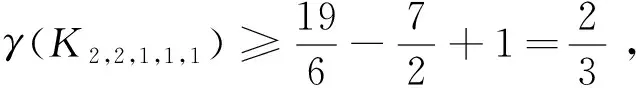

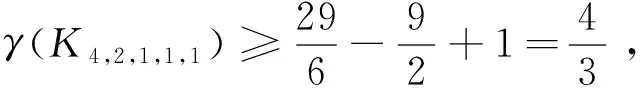



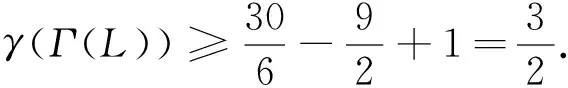


4 结束语

