考虑三维波纹度影响的深沟球轴承振动噪声计算方法研究
孙敏杰, 安 琦
(华东理工大学机械与动力工程学院,上海 200237)
深沟球轴承的波纹度误差是造成轴承振动继而产生噪声的重要因素,轴承的滚道波纹度具有空间三维性质。但长期以来对轴承波纹度引起的振动噪声问题一般都是简化成一维形式,无法实现精确计算。
Yhland[1]以外部激振力的形式来描述轴承波纹度的影响,并研究了轴承的线性振动问题。Aktürk[2]研究了内圈、外圈以及滚动体波纹度对轴承振动的影响,分析了波纹度数目与振动频率之间的关系。Harsha 等[3]研究了由轴承波纹度所导致的轴承非线性振动问题,发现当滚动体数目与外圈波纹度数目相同时轴承振动加剧。Sopanen 等[4]综合考虑了波纹度和弹流润滑的影响,建立了深沟球轴承的六自由度模型。Lynagh 等[5]通过理论和实验对滚动体尺寸误差、滚动体和内外圈滚道波纹度误差导致的轴承和转轴振动进行了研究。
Igarashi[6]通过测量声压发现噪声主要来自于轴承套圈与保持架。Ananthapadmanaban 等[7]通过试验获得了不同加工精度的轴承噪声频谱,并研究了在滚动和滑动状态下其不同的声学特性。Rho 等[8]将轴承视为无限长柱体,研究了无外载作用下圆柱滚子轴承的噪声特性。Ban 等[9]研究了在径向载荷作用下轴承油膜波动所产生的声压沿轴承径向的分布,揭示了声压与径向间隙、润滑油黏度之间的关系。涂文兵[10]利用边界元法,建立了轴承-轴承座系统的振动噪声模型,研究了承载区打滑状态下轴承的噪声特性。何磊等[11]采用专门从事噪声分析的CAE 软件Virtual. Lab 9A 对轴承的结构振动噪声进行了仿真。王培[12]提出了轴承声振耦合的算法,实现了对轴承声学特性的预估。
通过文献归纳可以看出,以往研究所建立的波纹度模型均只反映了轴承表面的一维特性。本文将通过力学分析,从三维角度构建轴承滚道三维波纹度模型,结合声学相关理论研究深沟球轴承的振动噪声问题。
1 计算模型构建
1.1 不考虑滚道波纹度误差时的力学分析
图1 所示为径向力作用下深沟球轴承力学模型,在径向力Fr的作用下,滚动体和内外圈滚道相互接触,产生接触变形。内圈中心由点O偏移到了位置O,其径向位移 δr在X轴、Y轴的分量为 δx、 δy,在方位角 φj处的套圈位移量( δr,j)为:δr,j=δxsinφj+δycosφj。

图1 深沟球轴承受力模型Fig. 1 Mechanics analysis of deep groove ball bearing
滚动体与内外套圈接触将会产生弹性接触变形,由文献[13]可知滚动体与内外圈滚道产生的弹性变形量 δi,j、 δo,j分别为:


其中Pe为轴承的游隙。根据受力平衡条件,内圈与滚动体之间的接触载荷分别在竖直与水平方向与所受到的外加载荷相互平衡:

其中Q为接触载荷,由式(1)可得:

通过式(2)、(3)、(4)、(5)可以求得理想情况下各滚动体的接触载荷Q的大小,同时也可以确定内圈的径向位移 δr。
1.2 考虑滚道波纹度误差时的力学分析
本文通过自相关函数法可以得到三维的随机波纹度表面。根据文献[14]取指数型自相关函数:
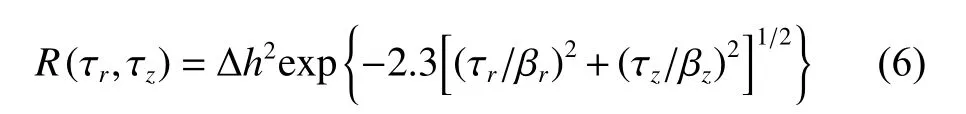
式中: Δh为波纹度的幅值;τr、τz为周向和轴向取样步长,βr、βz为相关长度。生成的波纹度表面如图2所示。

图2 轴承滚道表面波纹度示意图Fig. 2 Surface waviness schematic of bearing raceway
图3 所示为滚动体轴向位置示意图。由图3 可知,Obj为j号滚动体圆心未发生位移时的前球心位置,O′bj为发生位移后的前球心位置,ro为滚道外圈沟曲率半径,(Y′,Z′)为无波纹度存在时外圈滚道表面点的坐标,(Y,Z)为存在波纹度时该点相对应的坐标值。当轴承承受径向载荷作用时,由于滚道波纹度的存在,在中间平面滚动体受力不平衡,必然会向中间平面的两边发生窜动,当滚动体移动到一定的轴向位置,使得滚动体所受不平衡力分量相互抵消时,即为滚动体的实际平衡位置。

图3 滚动体轴向位置示意图Fig. 3 Axial displacement schematic of rolling body
滚动体在滚道内旋转,其与滚道所接触的轮廓随时间不断发生改变。在轴承旋转的任意时刻t,滚动体的上下表面与其接触的轴承内外圈表面可由一组函数来描述:



考虑接触点处内外圈滚道波纹度误差,在方位角φj处套圈位移量与各滚动体接触变形量的关系为:

其中: Δhi为接触点处内圈波纹度幅值; Δho为接触点处外圈波纹度幅值。

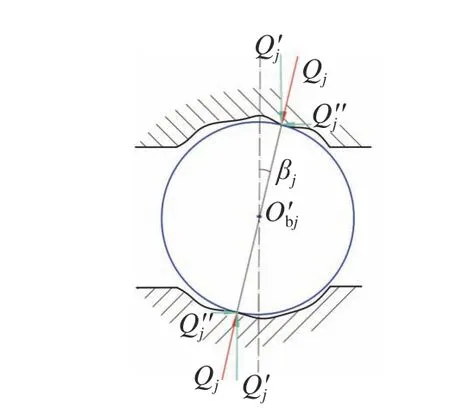
图4 波纹度影响下滚子受力平衡条件Fig. 4 Balance condition of balls under waviness

考虑波纹度影响时深沟球轴承受力模型如图5所示。假设轴承内圈受到的滚动体Z向载荷分量(Q)由转轴承担,即内圈沿着Z向不发生振动,根据轴承的受力平衡可知,内圈受到滚动体在竖直方向的作用力与所施加的载荷保持平衡:

图5 考虑波纹度影响时深沟球轴承受力Fig. 5 Mechanics analysis of deep groove ball bearing considering waviness
同理,内圈受到钢球在水平方向的分力相互抵消:

将各滚动体的变形协调关系代入受力平衡方程(11)、(12)中即可求得在考虑波纹度情况下各滚动体的接触载荷Q及内圈的径向位移 δr,同时将径向位移对时间求导可以获得内圈的运动速度。
1.3 声源模型建立
通过将轴承内圈和滚动体的振动进行Fourier 展开,可以得到不同幅值、频率和相位的简谐振动。深沟球轴承滚动体声源采用一阶球振声源模型,其辐射声压如式(13)所示。

式中:B1为一阶球诺伊曼函数系数;k为声音的波数;m为不同阶简谐振动的序数; θ 为各阶声波的初始相位;L为声压测点至轴承中心的距离; ω 为各阶声波的振动频率。
采用声学边界元方法研究内圈的声学特性,为了简化计算,对轴承内圈滚道进行简化,如图6 所示为离散后的内圈网格模型。

图6 轴承内圈边界元方法模型Fig. 6 Boundary element method model of bearing inner ring

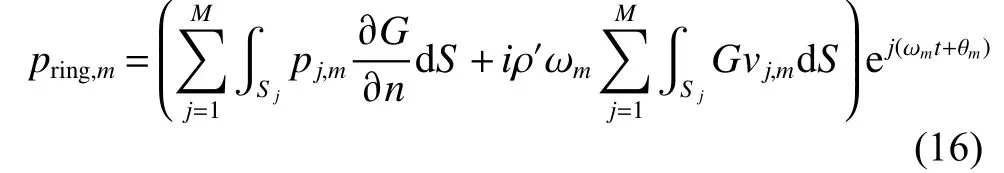
其中:pj,m为j球的声压值;vj,m为j单元的外法向振速。在求得了各阶简谐频率振动下内圈和滚动体的辐射声场后,复杂振动下各声源的辐射声压可以通过声压的叠加原理求得:
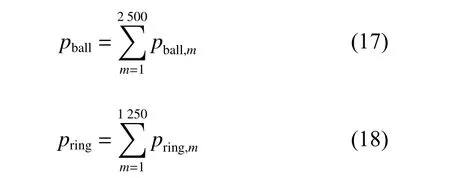
在求得了各声源的辐射声压以后,从声能的角度可得轴承内圈和滚动体总的合成声场,如式(18)所示:

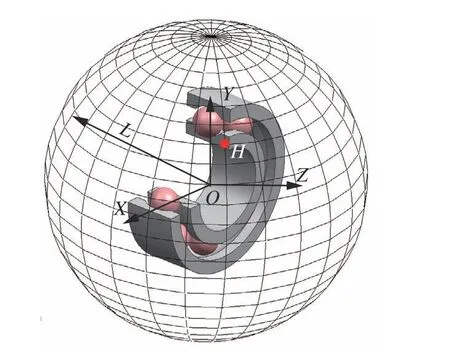
图7 轴承声压球面测点Fig. 7 Sound pressure field sphere points of bearing
2 算例研究
根据本文所建立的计算模型,以608 轴承为例对其进行算例研究,轴承的具体参数如表1 所示。

表1 轴承参数Table 1 Bearing parameters
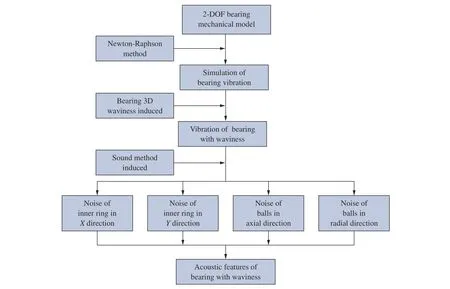
图8 轴承振动噪声算法流程图Fig. 8 Calculation flow chart for vibration and noise of rolling bearing
根据轴承声压级测试标准[18],轴承的旋转速度定为3 600 r/min,声压球面的测点半径L为50 mm。轴承内圈表面波纹度的幅值为1.0 μm,内圈表面离散为400 个单元,并且在所计算的最高频率内满足最大网格尺寸为波长的1/8 的要求。
根据已知的轴承几何参数和运动参数,求解得轴承内圈旋转频率fi= 60 Hz,滚动体旋转频率fb= 22.34 Hz,内圈相对滚动体的旋转频率fib=fi−fb= 37.66 Hz,滚动体通过外圈的频率fBPF=Nbfb=156.38 Hz,滚动体通过内圈的频率fBPFi=Nbfbi=263.62 Hz。
图9(a) 所示为内圈的轴心位移轨迹,图9(b)、9(c)分别为轴心轨迹在X轴方向和Y轴方向上的投影。由图可知,当不考虑波纹度的影响时轴心轨迹近似于椭圆,轴承内圈按一定的规律周期性地振动,振动频率等于滚动体通过外圈的频率fBPF。然而当考虑了轴承滚道的波纹度后轴承内圈中心偏离原来的轨迹进行无序运动,且振动的幅值远大于不考虑波纹度时的幅值。

图9 内圈轴心位移Fig. 9 Orbit of the inner ring center
图10(a)所示为滚动体球心的径向位移。由图可知滚动体的径向振动主要由两部分构成,一部分为轴承在运转过程中滚动体不断绕轴心作圆周运动时产生的周期性振动,其振动频率为滚动体的旋转频率fb,另一部分为由内外圈波纹度引起的高频分量。图10(b)所示为由波纹度引起的滚动体的轴向位移,滚动体绕中间平面往复振动。

图10 滚动体球心轨迹Fig. 10 Orbit of the ball center
图11(a)、(b) 所示分别为在球面测点处内圈X、Y方向振动分量产生的声场分布,图11(c)、(d)所示分别为滚动体径向及轴向振动的声场分布,图11(e)所示为轴承的总合成声压分布。由图可知内圈和滚动体由振动所产生的声压在空间中的分布是不均匀的,沿着内圈振动方向测得的声压级具有较大数值,而垂直于振动方向测得的声压等级较小。

图11 轴承内圈和滚动体的声压分布Fig. 11 Sound pressure level (SPL) distribution of inner ring and balls
图12(a)、(c)分别示出了内圈在X、Y方向振动所产生的声压信号,在对其进行傅里叶变换(FFT)后可以得到相对应的声压频谱图,如图12(b)、(d)所示。当考虑了滚道表面三维的随机波纹度后,声压频谱的成分十分复杂,其中在频率为157 Hz 附近出现了第一条峰值,此频率对应于滚动体通过外圈的频率fBPF。由图12(b)、(d)可知当频率低于fBPF时相对应的声压的幅值接近于零,当频率高于fBPF时出现了若干个峰值,其中部分峰值所在的频率与基频fBPF成倍数关系,部分峰值所在频率与外圈频率fBPFi成倍数关系,另外的一部分由波纹度的影响而产生。
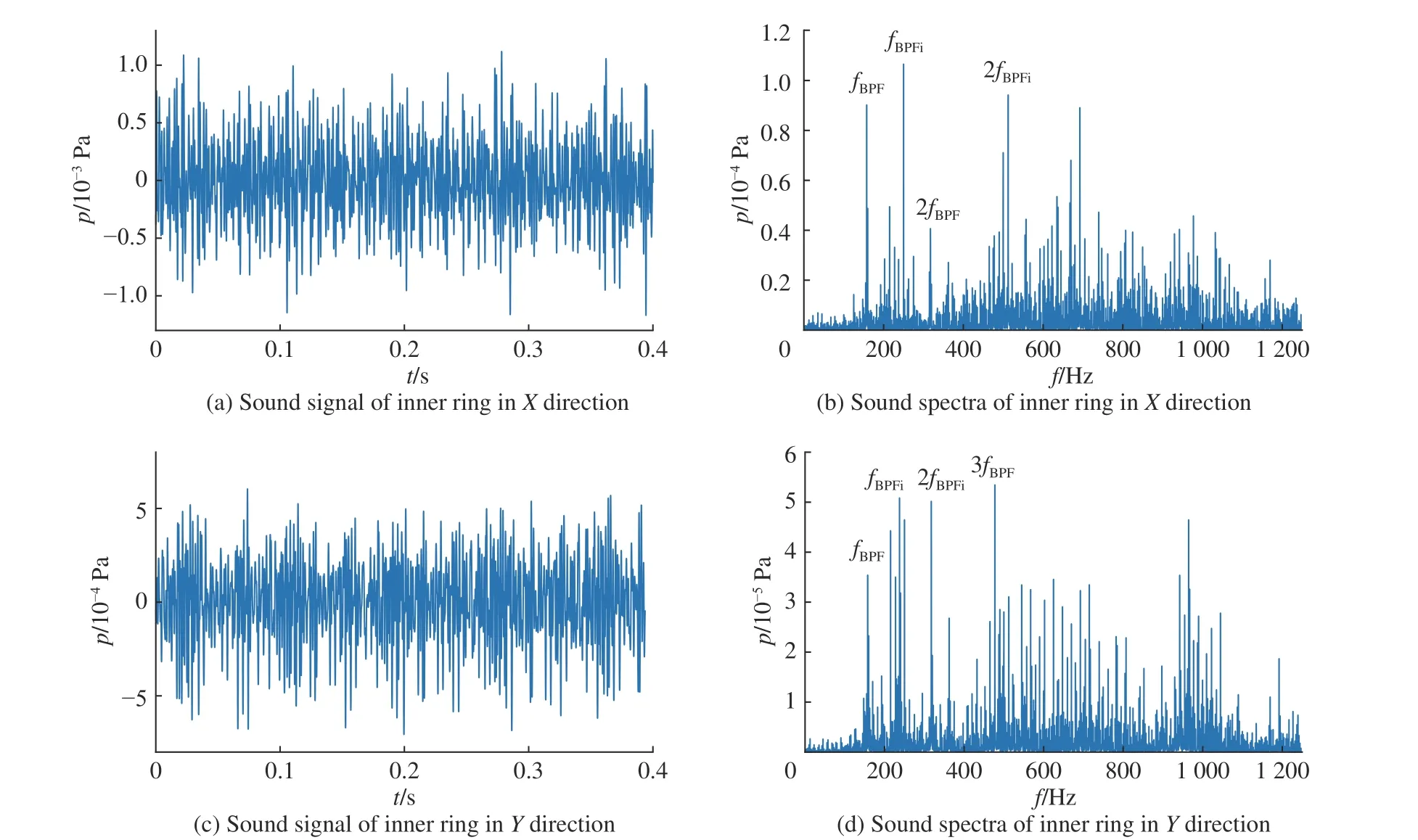
图12 测点H 处内圈的声压响应Fig. 12 Response of sound pressure for inner ring at point H
图13(a)、(b) 所示分别为在测点H处由单个滚动体在径向和轴向计算得出的声压信号。由图13 可知由于滚动体在振动的同时绕着轴心作圆周运动,声源与测点间的距离不断发生改变,从而使声压随着时间变化出现周期性的波动,其中径向振动产生的声压的波动频率为 2fb,轴向振动产生的声压的波动频率为fb。图13(b)、(d) 所示为对应的声压频谱图,可知在低频段(<500 Hz)和高频段(>1 000 Hz)声压所占比例较小,而中频段(500~1 000 Hz)所占的比例较大。

图13 测点H 处滚动体的声压响应Fig. 13 Sound pressure response for balls at point H
为了研究不同波纹度对深沟球轴承产生噪声的影响,根据JB/T 9 924—2014《磨削表面波纹度》标准[19],分别取值0.16、0.25、0.40、0.63、1.00 μm。图14 所示为在所选取的不同波纹度误差下测点处内圈沿X方向的声压响应及声压频谱,可知随着波纹度误差的上升,轴承内圈产生的噪声也随之增加,且在波纹度误差较小的情况下声压频谱主要由fBPF及其倍频所组成,而在波纹度误差较大时出现了fBPFi及其他高频成分。

图14 测点H 处不同波纹度内圈X 方向振动声压响应Fig. 14 Sound pressure response of inner ring in X direction with different waviness at point H
不同波纹度情况下深沟球轴承各噪声成分的峰值和RMS(Root Mean Spuare)值对比如图15 所示,其中波纹度误差为0 表示在正常轴承激励下得到的分析结果。由图可知各组分的声压值均随着波纹度误差的增大而增加,增速近似于线性且波纹度误差对滚动体轴向振动噪声的影响略大于径向振动噪声。

图15 测点H 处不同波纹度轴承声压响应成分对比Fig. 15 Comparsion of sound pressure for different components under different waviness at point H
3 结 论
(1)通过力学分析,建立了深沟球轴承内外圈滚道的三维波纹度误差模型,分析了在径向力作用下深沟球轴承的受力状态,建立了对内圈轴心轨迹及滚动体运动轨迹的计算模型。采用相应的声学理论,建立了对深沟球内圈和滚动体振动噪声定量计算的声学模型。
(2)通过具体算例,运用本文提出的声学计算模型,数值研究了深沟球轴承内圈和滚动体噪声的声辐射特性。研究表明内圈和滚动体的噪声辐射在空间中具有一定的指向性,且沿着其振动方向的声压级较大;通过对测点处各轴承组分的声压信号及频谱的分析,发现内圈的声压频谱主要出现了以fBPF及fBPFi为基频的倍频分量,并伴随波纹度引起的随机的高频成分,滚动体的声压频谱峰值则主要集中于500~1000 Hz 频率段;数值研究了不同波纹度误差对轴承各组分的声压响应影响,绘制了影响曲线,发现存在波纹度误差时的声压大于正常轴承的声压响应,且声压响应的峰值和RMS 值随着波纹度误差的增大而逐渐增大。
符号说明:



