基于自适应稀疏表示和保局投影的工业故障检测

邬东辉， 顾幸生

（华东理工大学能源化工过程智能制造教育部重点实验室，上海 200237）

随着科学技术的不断进步，现代工业过程日益大型化和复杂化，对工业过程的安全运行要求日益提高。为了提高生产效益、降低生产成本，人们对如何降低生产过程中潜在的危险性，提高工业生产的安全可靠性越来越重视[1-3]。故障检测与诊断作为化工过程异常工况管理最有力的工具，对化工过程的故障趋势进行分析、预测和恢复，为过程安全提供了一定的保障。故障诊断技术发展至今，基于机理模型的方法、基于知识的方法和基于数据驱动的方法[4]是研究故障诊断的三大方向。基于机理模型的方法需要对被检测系统的输入和输出数据构造数学模型，且该信息与正常运行状态无关，通过分析和处理被诊断系统中可以测得的有用信息和模型所表达的实际系统的先验信息的残差，实现过程的故障诊断。数学模型建立的精确与否是基于机理模型方法的关键之处，模型建立精度的高、低直接影响到监控效果[5]。基于机理模型的方法主要包括参数估计法 (Parameter Estimation, PE)[6]、状 态 估 计 法 (State Estimation, SE)[7-8]和等价空间法(Parity Space, PS)[9]。基于知识的方法利用人工智能相关方法，通过构建一些功能来学习和模仿监控过程中人类的思想、行为等，自动完成整个监控和诊断过程[1]。该方法将过程知识和相关理论相结合，虽然对模型的精度没有要求，但对过程知识存在依赖性，所以通用性有待提升。基于数据驱动的方法依据与数据相关的处理和分析方法来实现。该方法基于过程中获得的数据，通过分析和挖掘其内部特征来指导工作人员判断系统当前的运行状况，提取数据的有效特征信息来辨别是否发生故障，不需要建立精确的机理模型、不依赖过程知识[10-11]。多元统计是基于数据驱动方法常用的一类方法，包括主元分析 (Principal Component Analysis, PCA)[12]、偏最小二乘 (Partial Least Squares,PLS)[13]等。随着工业过程中检测和储存的数据维度不断增大，传统的多元统计方法在处理大样本、高维数据集的过程中，会出现运行速度慢、效率低、故障检测时数据的局部特征易丢失等问题。

针对上述问题，已有研究人员尝试利用流形算法对多元统计方法进行改进。Zhang 等[14]提出利用一种端到端的深流形到流形变换网络，以便于深层网络的批核优化。薛敏等[15]通过构建偏最小二乘、邻域保持回归(Neighborhood Preserving Regression,NPR)、局部全局主成分回归(Local and Global Principal Component Regression, LGPCR)3 种基础模型，提出了一种融合过程数据集全局与局部结构特征的集成质量监控方法；卢春红等[16]提出了非局部约束下的局部稀疏保持投影方法，利用稀疏编码获取表征全局结构信息的稀疏码，然后计算稀疏码的权重值，突出其对故障的贡献度，建立统计量进行故障检测。Zhao 等[17]提出了一种基于双谱局部保持投影的智能故障诊断方法，保局投影的引入极大地保留了双谱特征的高维特性，克服了传统双谱分析方法严重依赖专家经验的局限性，同时提高了诊断效率。

稀疏字典具有非常突出的数据特征提取能力，在众多的领域中表现卓越，尤其是在图像处理领域应用广泛[18]。Leal 等[19]将字典学习和稀疏编码相结合用于处理视觉检测问题。Lin 等[20]引入双稀疏字典的思想，提出了一种用于处理无线传感器网络的方法，通过稀疏编码提高数据采集的效率和可靠性。基于稀疏字典学习在数据降维方面的特点，近几年也有学者将稀疏字典学习应用到故障诊断中。李继猛等[21]在轴承的故障诊断问题研究中引入稀疏分解，使稀疏分解与正交匹配追踪算法相结合。郭小萍等[22]提出在多工况研究中，通过构建残差空间获取统计量，使模型的特征更加明显，利用稀疏编码构建全局模型，进行故障检测。

本文针对工业过程中检测和储存的数据维度不断增大，传统的检测方法存在处理速度慢、故障特征提取不明显等问题，提出了一种基于自适应稀疏表示和保局投影（ASRLPP）的故障检测算法。首先采用稀疏字典对数据集进行特征提取，构建残差空间；然后利用保局投影（LPP）算法在残差空间内进行降维，同时提取数据局部特征信息。在监测过程中，制定更新规则，利用控制限和局部离群因子(Local Outlier Factor, LOF)[23-24]对测试数据进行筛选判断，将检测到的正常工况数据集用于更新训练集，动态调整控制限。数值仿真例子和TE 过程仿真验证了本文方法的有效性和优越性。

1 稀疏字典和保局投影算法

1.1 稀疏字典

稀疏表示理论的基本思想是将正交变换中固定的基函数用过完备的字典来取代，使数据集的特征得到提取[22,25]。

1.2 LPP 算法

流形学习通过发现高维数据中的低维流形特征，将所要研究的对象降维到低维空间，同时保持局部特征[29]。LPP 算法主要分为3 个步骤：构建邻接图、选择权重、计算投影矩阵。

假设数据集X∈Rm×n，LPP 方法就是计算投影矩阵A，使得投影后的低维空间Y∈Rd×n(d＜m)能够满足yi=ATxi。

约束条件：

1.3 T2 统计量

T2统计量是一种可以用单变量控制图的形式来监测多变量工况的变量，利用主元模型内部的主元向量模的波动，用于反映多变量变化的情况[30]。其定义如下：

当控制限满足式（11）时，表示过程运行在正常状态下；否则认为过程处于故障状态，发出报警信号[31]。

2 ASRLPP 自适应模型故障检测

2.1 基于稀疏字典和保局投影的特征提取

假设有正常样本数据Xtrain∈Rm×n作为训练集。由式（1）对采集到的正常样本数据进行标准化处理，采用稀疏字典和保局投影结合算法（SRLPP）对标准化后的样本数据提取特征。设置初始字典集，一般考虑随机抽取正常样本数据集作为初始字典集，同时设定稀疏度s，利用正交匹配算法计算初始字典的稀疏编码，保持字典D不变。由式（2）计算得到相应的稀疏编码矩阵 α ，再保持 α 不变，更新迭代字典D，重复上述操作获得字典和稀疏编码矩阵。利用稀疏系数矩阵和更新后的字典求得原始样本的近似值，并计算残差，构造残差空间。将产生的残差空间利用LPP 算法进行局部特征提取和数据降维，由式（8）计算降维后的投影矩阵A。对于特征提取和降维后的矩阵A，利用核函数计算其T2统计量获得控制限Tlim。

2.2 自适应更新规则

3 故障检测步骤

ASRLPP 故障检测分为离线建模和在线检测两个步骤, 如图1 所示。

图1 故障检测流程图Fig. 1 Flow chart of fault detection

离线建模：

Step 1 采集正常样本数据组成训练集X∈Rm×n，同时进行标准化处理。

Step 2 设置初始字典D和稀疏度s，通过更新迭代得到更新字典和稀疏编码矩阵；计算得到残差，构造残差空间；利用LPP 进行降维，获得矩阵A。

Step 3 对于特征提取和降维后的矩阵A计算统计量的控制限Tlim。

在线检测：

Step 1 收集待检测数据Xtest进行标准化处理，将处理后的数据集作为测试集。

Step 2 计算得到待测数据集的稀疏矩阵和残差矩阵，利用建模中产生的投影矩阵进行降维得到Atest。

Step 3 计算降维后矩阵的T2统计量以及 局部离群因子，判断是否满足更新条件，如果满足，则将测试数据更新到训练集，调整控制限，若不满足，则判断为故障样本，返回Step 1。

复杂度分析：对数据集X∈Rm×n进行标准化处理，复杂度为O(n) 。迭代更新字典和稀疏矩阵获得残差空间，复杂度为O(ns) 。利用LPP 算法进行降维时分为两步，k 近邻搜索，时间复杂度为O((n+k)m2) ，计算特征值将m维数据降到d维，时间复杂度为O((n+d)n2) ，故LPP 算法复杂度[32-33]为O((n+k)m2+(n+d)n2) ；求 取 控 制 限，时 间 复 杂 度 为O(n2) ；故ASRLPP 故障检测算法的整体算法复杂度为O(n+ns+(n+k)m2+(n+d)n2+n2) 。

4 仿真实验

通过一个数值例子和TE(Tennessee- Eastman)过程验证ASRLPP 算法的有效性。

4.1 数值例子

采用文献[34]中的数值仿真例子进行测试，具体结构如下：

其中包括5 个变量x1、x2、x3、x4、x5和5 个相互独立且服从N(0,0.01) 的白噪声e1、e2、e3、e4、e5。设定工况1 下s1为 均 匀 分 布U(-10,-7) ，s2为 高 斯 分 布N(-15,1) 。首先在正常运行状态下，采集800 组正常样本作为训练集;再采集800 组数据作为测试样本，测试样本设定在第401 个数据点处引入两种故障。故障1：系统正常状态运行下，在x5加上幅值为4 的阶跃信号；故障2：系统正常状态运行下，给x1加上0.02(i-400) 的斜坡信号。

分别采用LPP、SRD[22]、ASRLPP 算法进行检测，其中LPP 是基础降维算法，SRD 是对稀疏字典改进后的故障检测算法，该算法的检测指标为D2。为使算法比较更具公平性，进行参数选择。对于有降维操作的算法降维后的维数为2，利用k 近邻法构建关系矩阵，近邻参数k=5，T2统计量置信度均设为0.99，初始字典维数设置为400。

工况1 下两种故障的数值检测结果如表1 所示。可以看出，SRD 算法和ASRLPP 算法相对于LPP 算法，故障1 和故障2 都获得了较低的漏报率（MAR），提供了比较理想的检测结果，说明检测性能都有较大提高；比较SRD 算法和ASRLPP 算法，对于两种故障，虽然SRD 算法有较低的漏报率，但是误报率（FAR）较高，相比之下ASRLPP 算法能保持非常低的误报率。

表1 工况1 下数值例子故障检测结果Table 1 Fault detection results of numerical examples under condition 1

图2 示出了LPP 算法和ASRLPP 算法对故障1 和故障2 降维后的PC1、PC2 散点图。从图中可以看出，LPP 算法对数据降维后，故障数据点和正常数据点并没有实现很好的分离，故检测效果较差；ASRLPP 算法对数据降维后，故障数据点和正常数据点分离明显，能进一步区分故障数据点，使得后续的故障检验操作更准确、有效，进而有助于提高故障的检测率，证明了该算法的有效性。

图2 故障1 和故障2 下两种算法的PC1 和PC2 散点图Fig. 2 PC1 and PC2 scatter diagrams of two algorithms under fault 1 and fault 2

改变数值测试的运行工况，设定工况2 下s1为 2cos(0.08k)sin(0.006k) ，s2为 sign[sin(0.03k)+9cos(0.01k)] ，其中k表示采样范围。同样在正常运行状态下，采集800 组正常样本作为训练集;再采集800 组数据作为测试样本，测试样本设定在第401 个数据点处引入两种故障，故障1：系统正常状态运行下，给x5加上幅值为4 的阶跃信号；故障2：系统正常状态运行下，给x1加上 0 .02(i-400) 的斜坡信号。在工况2 下数值例子的故障检测结果如表2 所示。图3示出了3 种算法对故障1 和故障2 的检测结果。

从表2 和图3 中可以看出，在工况2 下，SRD 算法和ASRLPP 算法相比于传统的LPP 检测效果更加优越，同时ASRLPP 能获得更低的误报率和漏报率，说明其检测效果更好。表3 对比了工况2 下的两种算法在不同字典维度下故障1 的检测结果，其中SRLPP 为未引入自适应更新规则的基于稀疏字典和保局投影算法，用于验证ASRLPP 算法中引入自适应更新规则的检测效果；分别设置初始字典维数为100、300、500、700，比较ASRLPP 和SRLPP 的误报率、漏报率，从表中可以看出，当初始字典维数较低时，SRLPP 算法的检测结果较差，分析认为当初始字典维数较低时，利用稀疏字典提取数据集特征的效果不佳，导致数据集的部分特征被遗漏，所以影响故障检测效果；而引入了自适应更新规则后，即使初始的字典维数较低，但通过自适应更新规则在检测过程中不断地优化初始训练集，使对故障1 的检测误报率和漏报率都保持较低，所以引入自适应更新规则对算法的稳定性有进一步的提高。

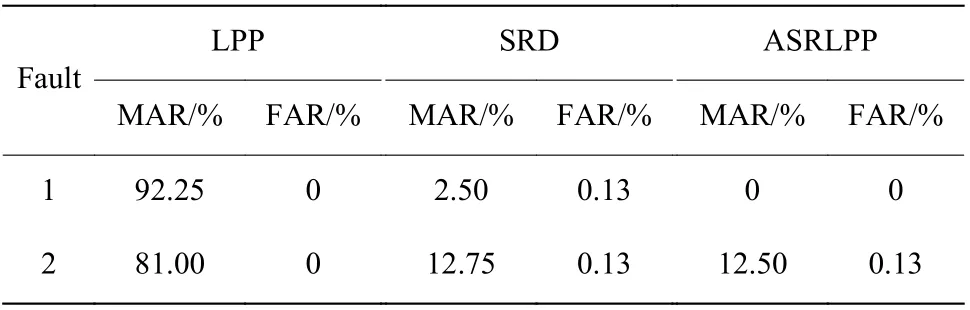
表2 工况2 下数值例子故障检测结果Table 2 Fault detection results of numerical examples under condition 2

图3 3 种算法对故障1 和故障2 的检测结果Fig. 3 Detection results of fault 1 and fault 2 under three algorithms

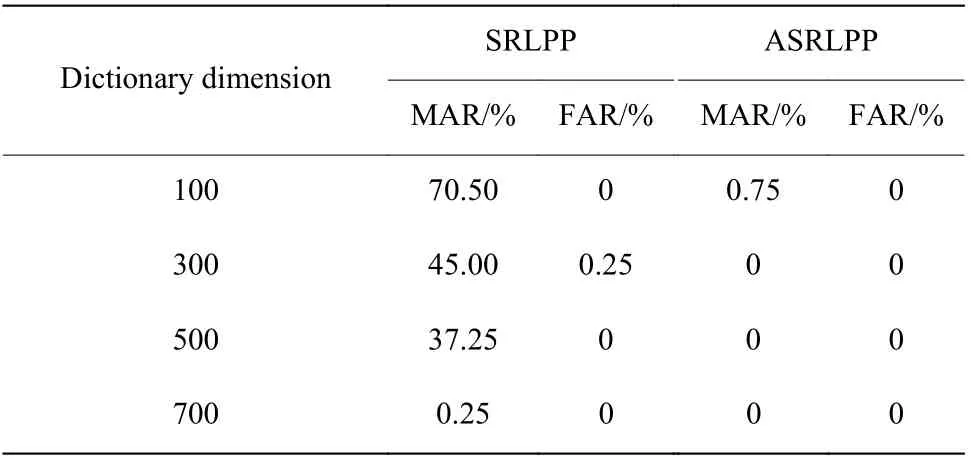
表3 两种算法在不同字典维度下故障1 的检测结果Table 3 Fault 1 detection results of two algorithms in different dictionary dimensions

从表中可以看出，ASRLPP 算法在特征提取和分离故障点方面具有一定的优越性，而且在保证获取较低漏报率的同时能控制极低的误报率，相较于其他算法具有更高的可靠性。

4.2 TE 过程仿真

TE 过程主要包括冷凝器、反应器、汽提塔、汽液分离器和循环压缩机5 个操作单元，共包括12 个操作变量和41 个测量变量。TE 过程还包含有预先设定的故障21 个，见表4，表4 中示出了前20 个故障用于算法性能的比较。采集TE 过程正常工况和20 个故障下的数据，其中正常工况和每个故障下的数据均采集960 个，故障测试集均在第161 个样本引入故障。

表4 TE 过程的20 个预设故障Table 4 20 preset faults of TE process

分别采用LPP、SRD、SRLPP、ASRLPP 算法进行检测。为保证对比实验的公正性和有效性，设定每个对照算法降维后的数据维度保持一致，设定降维后的维度为25 维，利用k 近邻法构建关系矩阵中法在SRLPP 算法的基础上可以进一步地降低误报率，提高检测准确率。

图4 示出了3 种算法对故障4 的检测结果图。

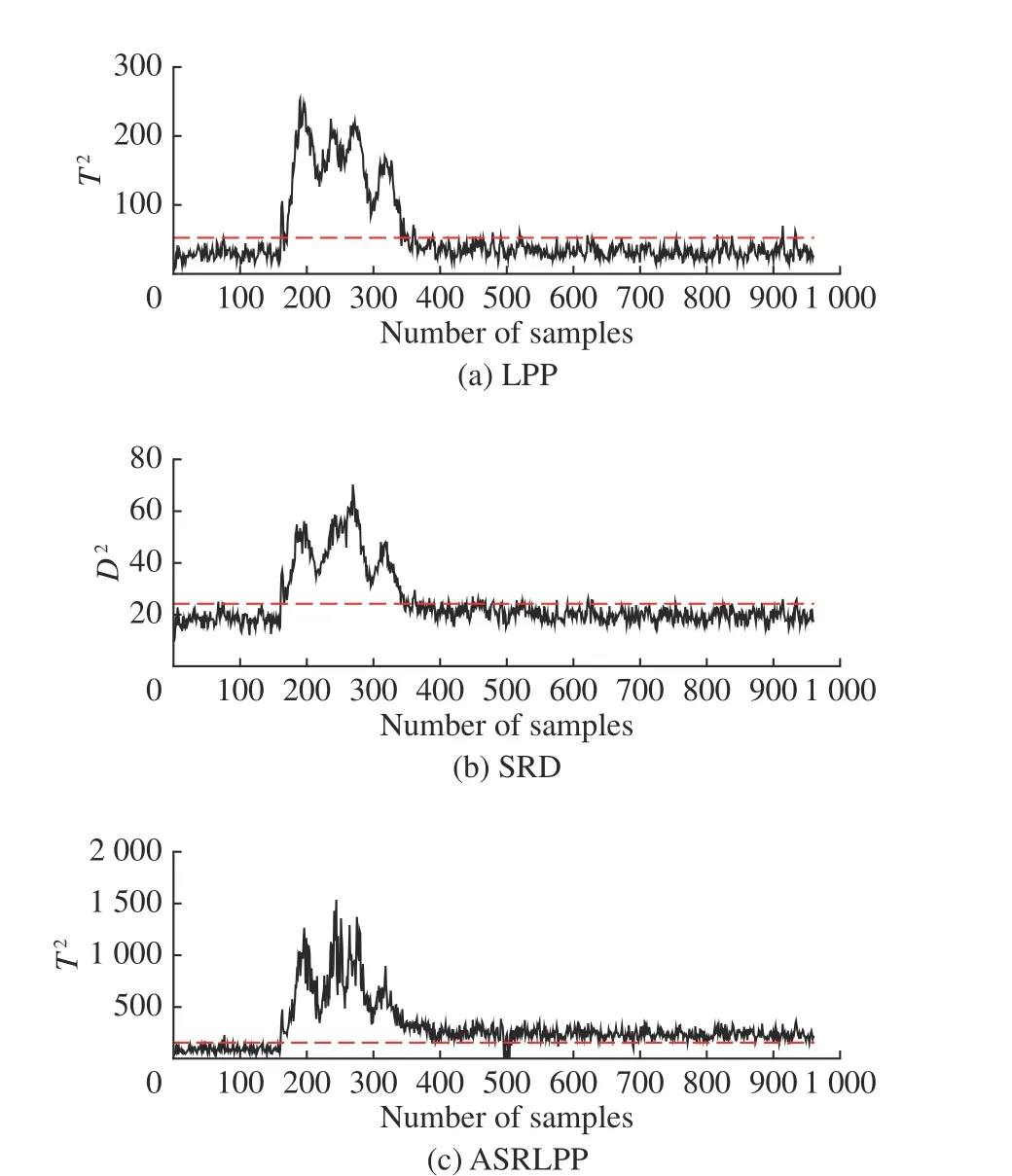
图4 故障4 在3 种算法下的检测结果Fig. 4 Detection results of fault 4 under three algorithms

表6 示出了3 种算法的故障检测时刻，检测时刻间隔3 min，表6 中数值表示第n个时刻开始，算法检测到故障信号。从表中可以看出，ASRLPP 算法的整体故障检测时刻明显早于其他两种算法，特别是对于一些较难检测的故障，如故障17、18、19、20 等，ASRLPP 算法都能获得较为准确的检测时刻，说明ASRLPP 算法的可靠性和准确性更高。从表4可知，故障5 表现为一种反应器冷却水入口温度的变化，该过程的干扰类型为阶跃变化，同时控制器对于该变量有较大的补偿效果。在实际过程中，如果发生故障，检测算法能迅速捕捉到故障发生，但是在350 个采样点过后，控制器的补偿作用会将检测量拉回到报警线以下，使系统无法继续检测到故障，这就造成了大量的漏报。本文提出的ASRLPP 算法能够在控制器补偿后仍能使检测量处于报警线以上，维持故障警报，保证系统的可靠运行。故障19 属于随机故障类型，对于该故障，上述方法均有较高的漏报率，分析认为，故障19 数据类型包括非高斯数据类型，当数据未知波动比较明显时，利用局部保局无法有效地区分离群点，同时不利于稀疏字典提取特征。ASRLPP 算法对易检测故障能获得比其他算法 的近邻参数k=5，SRD 的近邻样本设为5，T2统计量置信度均设为0.99。取960 组正常数据集作为字典的初始训练集，初始字典取其中的600 个。

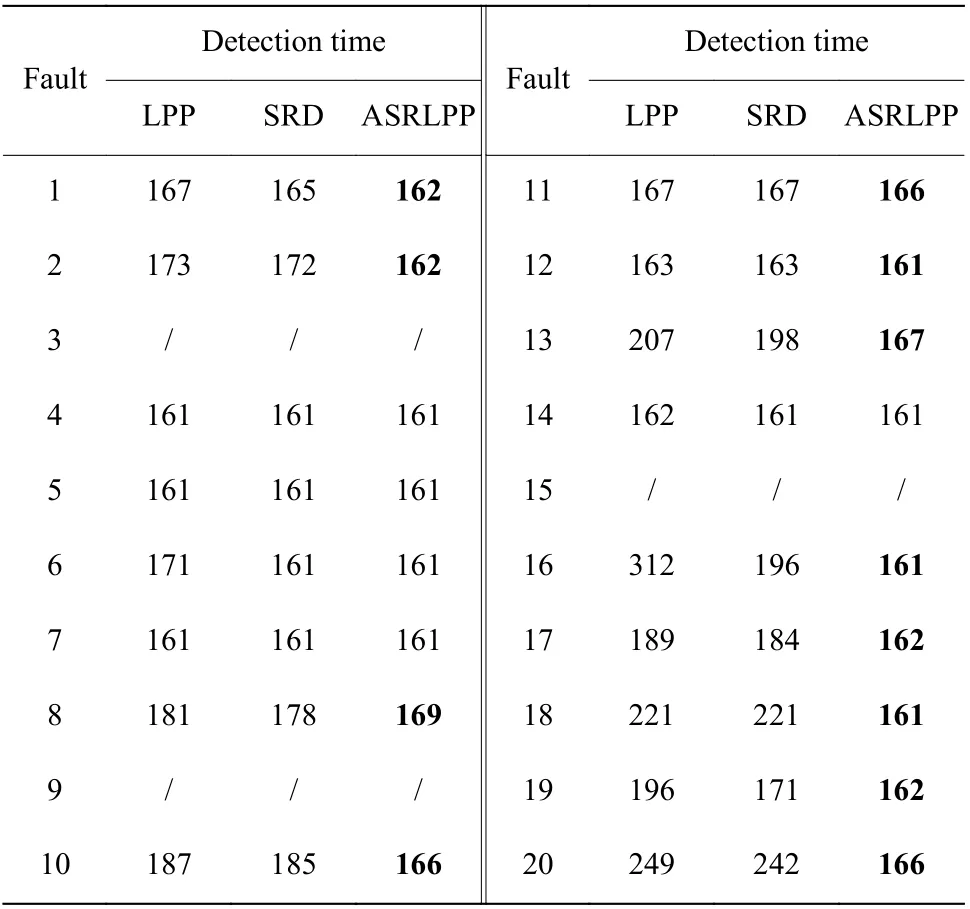
表6 TE 过程故障的检测时刻对比Table 6 Comparison of detection time on TE process

表5 示出了20 种故障（除故障3、故障9 和故障15 外）的漏报率、误报率检测结果，表中的数据为10 次运行结果的最优值。

从表5 可以看出，对于TE 过程中的20 种故障，ASRLPP 算法整体上在漏报率方面较LPP 和SRD 算法都有明显的降低，如故障5、10、11、16、19、20 等，ASRLPP 算法相比于以上两种算法都有较大的提高，特别是对故障5 的检测效果提高显著；对于容易检测的故障，如故障1、2、4、8、12、13、17、18 等，ASRLPP 算法能保证非常高的检测率，检测的准确性和精确性相比以上两种算法也基本都有提升，说明ASRLPP算法有一定的可靠性。从表中也能看到，虽然LPP 表现出很低的误报率，但是其整体的漏报率很高，算法的可靠性不高。对比表中SRLPP 和ASRLPP 两种算法的检测结果，可以发现ASRLPP 算更低的漏报率，是因为在故障检测的同时能利用数据点不断更新训练集，调整控制限。对于较难检测的故障，由于其本身的模型自适应能力受到限制，故不能获得非常理想的检测效果。

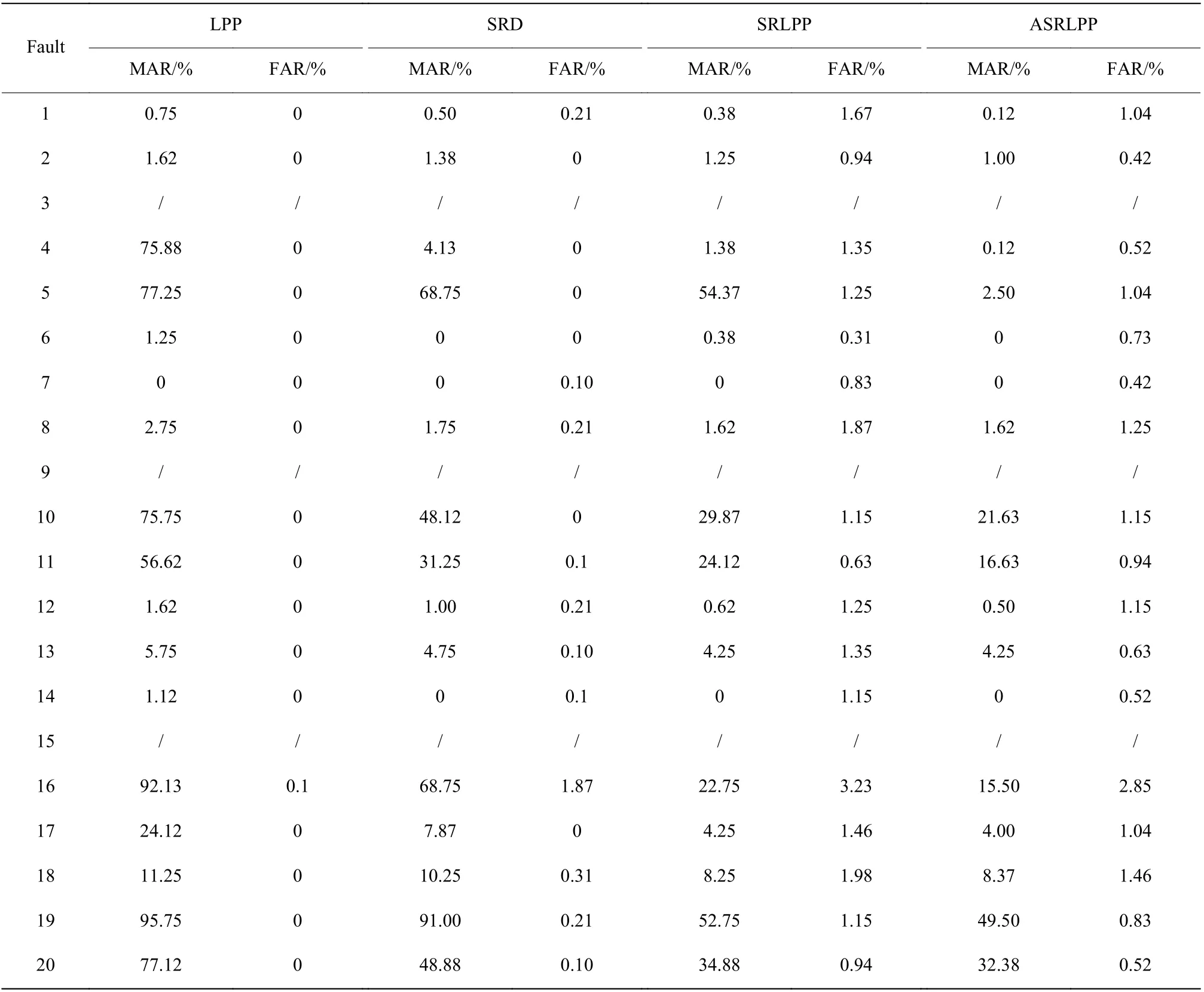
表5 故障检测结果Table 5 Fault detection results

5 结 论

本文提出的ASRLPP 故障检测算法在稀疏字典的基础上引入保局投影LPP 算法，将局部特征提取算法和全局特征提取算法相结合，从而对数据集的特征做到更有效的提取。同时在检测过程中，提出自适应更新规则，在实时的检测过程中，不断更新模型，调整控制限，进而使故障检测更加精确，有效提高故障的检测率。ASRLPP 算法所表现出来的对数据的特征提取和降维能力也为处理大数据、高维数据集等故障检测提供了一种解决思路。