亚音速喷流出口扰动对湍流与声场模拟的影响
许 聪, 刘琪麟, 赖焕新
(华东理工大学机械与动力工程学院,上海 200237)
作为气动声学的基本问题,喷射流动及其噪声的准确预测一直是国内外该领域的研究热点。对于实际的航空发动机,尾气喷流从涡轮到喷管出口的距离较短,而且在喷口处即为完全湍流状态,但相关的边界层厚度或湍流强度等湍流参数难以用实验测量得知[1]。数值计算方面,由于计算资源的限制,目前还难以一体化地计算上游叶轮机械和下游喷流的流-声场;喷射流动及其噪声问题仍只能单独考虑。而对于喷流模拟,上述湍流实验参数的缺乏使得数值合成湍流来流缺少依据,Bogey 等[2]的研究表明,喷口初始状态相关来流条件的准确性严重影响远场噪声的预测结果。实际喷管出口往往是湍流状态,而过去关于喷流计算的初始条件多为层流状态。文献[3-4]的结果显示层流的初始剪切层可导致远场总声压级的预测值与实验值有5~10 dB 的误差。层流的初始状态导致喷流发展中存在层流向湍流转捩,该现象会产生额外的低频噪声[5],但实际喷流下游并不存在这种流动过程。因此,数值合成湍流的喷管出口,从而准确预测湍流的混合层流动特性至今是喷流噪声研究的重点[6]。文献[7-8]将喷管包含在计算域内,试图让其自由发展得出湍流来流,但商用飞机发动机的喷流和全尺寸实验中的喷流中并没有这样的发展段[2]。因此,在喷流数值计算中如何利用人工扰动触发转捩,使其在尽可能短的范围内接近自由湍流条件,是当前喷流模拟普遍采用的策略,也是实现喷流大涡模拟准确预测的关键。
目前文献中对于喷管流动常用的方法有两种。一种是在流动中加入大尺度涡结构相关特征量的合成湍流[9-10],这一类方法可以使流动快速进入自相似区域进而改善预测结果,但是扰动作用随着大尺度湍流结构破碎而消失,不能准确预测下游剪切层流动特性。另一种较普遍采用的是基于不稳定本征模态的扰动方法[11-12],该方法借助于喷流中不稳定模态来触发湍流。相对于前者,后者合成的来流更符合实际喷管的流动条件,使喷流下游的特性也与实验一致,但是这种方法会增强近场湍流水平,进而导致远场噪声预测过高。Bogey 等[13-14]提出的多种周向模态组合的涡环扰动克服了这一问题,该方法对于主导流动的轴对称模态不敏感[15],并且可以降低模拟中预测过高的脉动和声压水平。但是受到扰动方式和施加位置的限制,只能在来流边界的下游一段距离开始起作用,且在与实验对比时,需要人为地减去涡环流向位置。
为了改善从喷口位置开始的全场预测结果,更早地触发向湍流过渡,本文将Hu 等[11]基于线性不稳定性分析得出的平行射流入口扰动扩展应用到圆口喷流,同时结合周向模态快速触发的优势,得出一种圆口喷流的多模态线性不稳定性来流扰动方法,以克服涡环扰动的上述不足。在此基础上,本文采用大涡模拟(LES)方法研究出口声学马赫数Ma=0.75、雷诺数ReD=8.7×105的喷流,将该扰动与Bogey 等[13]的涡环扰动以及来流无扰动的3 种工况进行对比分析,并采用已有的实验结果进行验证,研究比较3 种流动条件对该喷流流动和噪声预测准确性和有效性的影响。
1 计算设置
1.1 物理模型及网格划分
本文计算的圆口喷管出口直径Dj=50 mm[16],基于喷口速度(Uj)及远场声速(α∞)的Ma=Uj/a=0.75 ,基于喷口直径的ReD= ρUjDj/μ=8.7× 1 05,计算域示于图1 中。其中, ρ 为密度, μ 为动力黏度。坐标原点位于喷管出口的圆心处,计算域总长度为97.6Dj,其中喷管长度7.6Dj,渐扩段长度50Dj,缓冲区长度40Dj,计算域入口宽度为20Dj,出口宽度为40Dj。采用结构化网格,对剪切层区域进行了网格加密,网格节点数为 3 .5×106。本文前期已经通过外推法评估网格质量,结果表明该套网格可以分辨出唇线上80%以上的湍流脉动动能,满足LES 的质量指标要求[17]。
1.2 计算方法
大涡模拟计算采用商用软件Fluent,计算时选用Density-Based 求解器,扩散项和对流项分别采用中心差分和高阶迎风格式,时间采用隐式推进。初场由雷诺时均模拟给出,后续LES计算采用Smagorinsky-Lilly 亚网格模型,量纲为一时间推进步长为0.005Dj/Uj,对应全场CFL(Courant-Friedrichs-Lewy)≤1。经过时长为300Dj/Uj的发展,认为渐扩段已排除初始流场的影响,之后开始进行湍流量的采样统计,统计采样时间持续150Dj/Uj。采用FW-H 方程计算远声场,Mendez 等[18]提出该方法要求声源面需要包含绝大部分含能结构,但又不能过大而影响截止频率。基于湍流近场的涡量轴截面分布,取声源面流向范围25Dj,入口区域半径2Dj,出口区域半径4Dj。监测点位于r=30Dj和r=50Dj的两个同心圆面,圆心为喷管出口中心,流向监测角θ取30°~150°,测点和声源面位置如图1 所示,内部虚线为声源面。
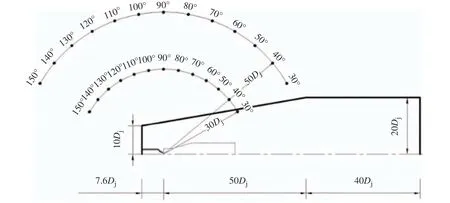
图1 计算域及测点示意图Fig. 1 Computational domain and measuring point positions
1.3 边界与扰动条件
本文计算了3 种不同来流条件下的圆口喷流,边界条件均为:入口边界给定总温320.4 K 和总压147 059.9 Pa,出口为静压边界,喷管壁面采用绝热无滑移条件,其他边界均给定远场静压进口条件,环境压力p∞=101 300 Pa,环境温度T∞=288 K,对应a∞=340 m/s。其中工况Nopert 的流场中无扰动施加是本文用作对照的基础工况,更多计算细节前期工作[17]已给出,工况Pert1 中加入来自Bogey 等[13]的涡环扰动,工况Pert2 中加入改进的多模态线性不稳定扰动。
工况Pert1 扰动计算式:


工况Pert2 的来流扰动即本文提出的以平行喷流扰动[11]为基础改进多模态线性不稳定扰动方案。Hu 等[11]基于线性不稳定性分析,得出了一种平行射流入口的单一模态扰动方法,为使其可应用于圆口喷流,本文考虑原扰动参数已经优化,因此首先对该扰动的流向分量保留,横向分量则改造为圆口喷流的径向。考虑多模态快速触发湍流的优势,本文将原扰动方法的单一模态修正为周向多模态组合,得到一种改进的多模态线性不稳定入口扰动,轴向和径向扰动速度的计算式如下:

在式(3)和(4)中,a1=0.33,a2=0.4,b=6, ω =2Uj/Dj,t为时间,扰动施加位置为喷口处,其余参数均采用涡环扰动中的优化数值[13]。采用软件Fluent UDF 将两种速度扰动施加在计算域中相应位置。
2 流场特性
2.1 平均流动特性
为方便表述,本文做如下规定:u和u0分别表示轴向速度及其脉动,v和v0分别表示径向速度及其脉动; h ·i 表示平均值,下标t和θ分别表示时间和周向平均。图2 和图3 分别示出了3 种工况下轴向速度的流向和径向分布,各计算工况与实验中的势流核长度如表1所示。由表1 可得,3 种工况的轴向速度预测结果与文献[16]中实验结果吻合良好,Pert1 的势流核长度Lc/Dj为5.52,最接近实验值6.5,Pert2 次之,Nopert 差距最大。此外,径向分布中,两种扰动工况比无扰动结果也有明显改善。以上结果表明本文所采用的计算方法及边界条件合理有效。

表1 势流核长度Table 1 Lengths of potential core
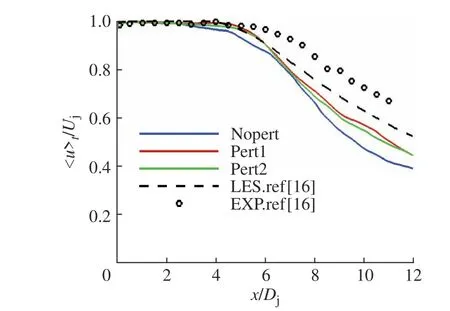
图2 中心线上轴向速度分布Fig. 2 Axial velocity distribution along centerline
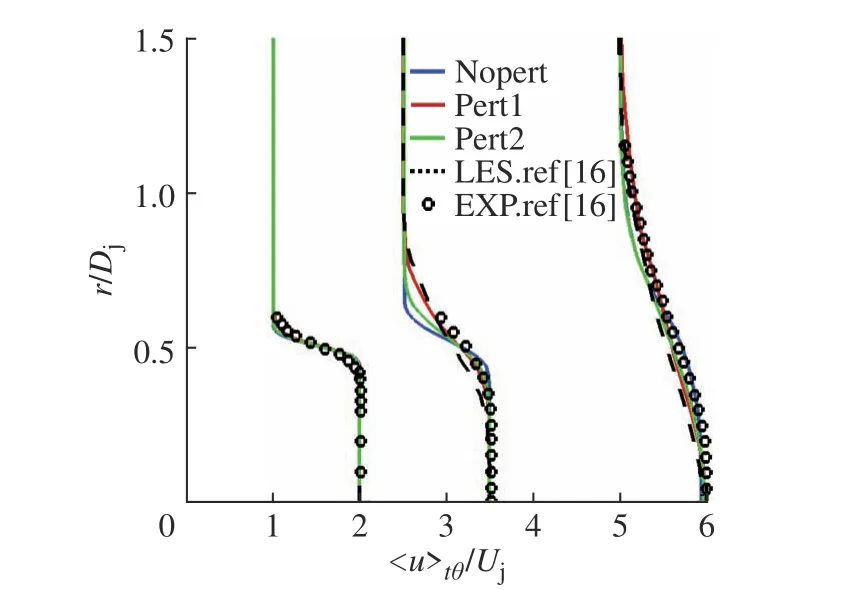
图3 x/Dj 为1、2.5、5 处轴向速度径向分布Fig. 3 Radial distribution of axial velocity at position x/Dj=1, 2.5, 5
剪切层速度半值宽r0.5是衡量剪切层发展的一个重要指标,其斜率反映剪切层的增长速率。从图4剪切层半值宽的轴向分布中可以看出,Nopert 中存在斜率明显不同的两个阶段,这种转变是层流剪切层中涡配对引起的转捩[19]。加入扰动后,两扰动工况的剪切层增长速率在近喷口区域升高,而在势流核下游降低,使剪切层半值宽整体上呈现无突变的缓慢增长,表明转捩在喷口附近短距离内已经完成,符合自由湍流的发展机制,形成了接近真实喷流的湍流来流。

图4 剪切层半值宽的轴向分布Fig. 4 Axial distribution of shear layer half-width
为了验证该现象,图5 示出了350Dj/Uj时刻的瞬态涡强的轴截面分布。从图5 涡量的轴截面分布中可以看出,Nopert 的涡配对在流向3Dj~4Dj发生,图中用虚线框标识出了这一区域,该位置对应剪切层半值宽斜率的转变,标志着层流向湍流过渡的开始。图5(b)和图5(c)中的Pert1 和Pert2 工况并没有配对现象,在x/Dj<3 之前,喷流剪切层已剧烈混合,处于完全发展的湍流状态,与均衡发展的剪切层一致。图6 示出了350Dj/Uj时刻x/Dj=2 截面瞬态涡强分布。从图6 可以看出,涡量在横截面x/Dj=2 的分布中,也可观察到Nopert 的喷流仍处于势流状态,涡量呈现规则的环状分布;而两扰动工况的旋涡周向不稳定性增强,这是由于加入的速度扰动破坏了流动稳定性,使流动与周围流体之间的掺混加剧。这些现象表明加入的扰动有效触发了流动快速转捩,形成了符合实际的湍流喷流。
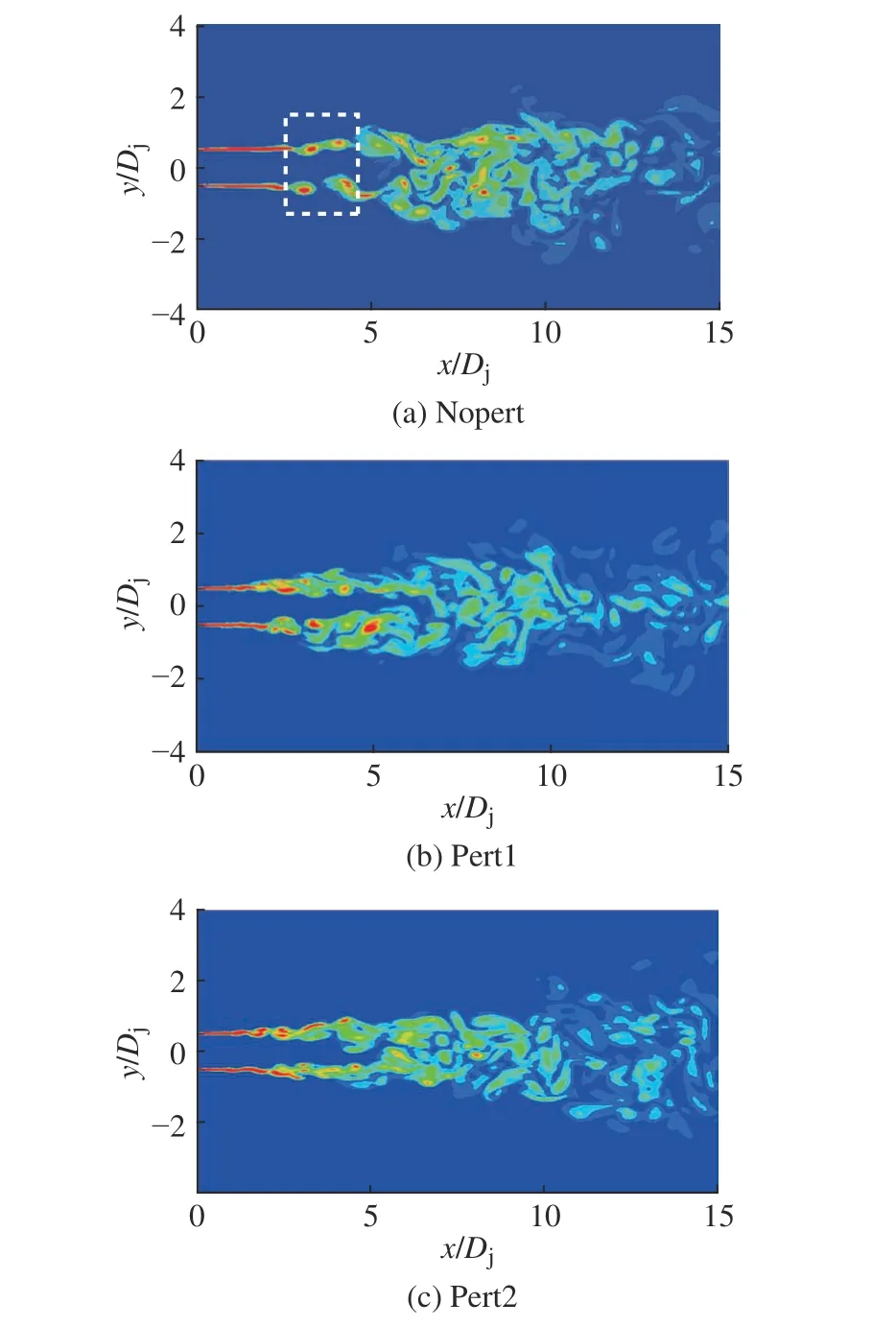
图5 t=350 Dj/Uj 时刻瞬态涡强的轴截面分布Fig. 5 Instantaneous vorticity magnitude distribution in axial section at t=350 Dj/Uj

图6 t=350 Dj/Uj 时刻x/Dj=2 截面瞬态涡强分布Fig. 6 Instantaneous vorticity magnitude distribution in the plane x/Dj=2 at t=350 Dj/Uj
2.2 喷流涡结构
喷射流动中,相干结构主导动力学以及声学特性,为了研究扰动对涡结构演化过程的影响,采用Q判据等值面进行可视化。图7 为Nopert、Pert1、Pert2 这3 种工况下Q判据等值面以及近喷口流域的局部放大图,颜色由蓝到红表征为从0 到Uj进行着色。从图7(a)示出的Nopert 工况中可以观察到环状涡形成、涡配对到失稳破碎的完整级串过程,在流向x/Dj为1~4 范围内有轴对称的涡环。而对于图7(b)和7(c)中两扰动工况,涡环的对称特征已不再明显,分别从Pert2 出口和Pert1 出口下游x≈Dj破碎成小尺度结构。施加扰动的射流均识别出了更细致的涡结构,物理现象更符合湍流来流的实际,再次证明了施加的两种扰动的有效性。
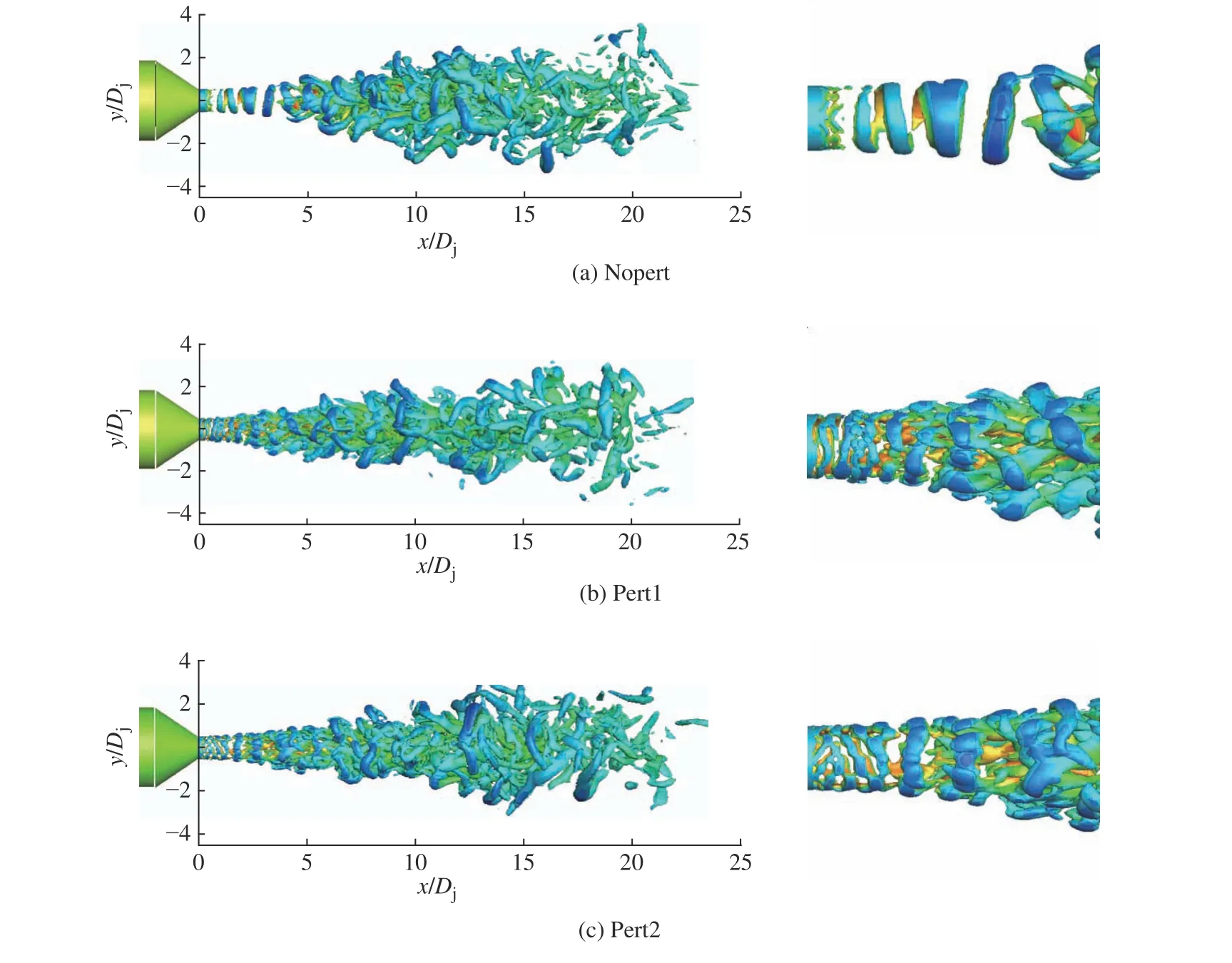
图7 t=350 Dj/Uj 时刻Q 判据等值面Fig. 7 Iso-surface of Q-criterion at t=350 Dj/Uj
2.3 湍流特性比较
2.3.1 空间分布 图8(a)和8(b)分别给出了轴向速度脉动和径向速度脉动沿中心线分布,其中rms 为均方根。3 种计算工况的速度脉动水平均高于实验结果,且峰值位置向上游移动,这与中心线上快速的速度衰减而导致的黏性耗散有关。在x/Dj<3 流域,Pert1 和Pert2 的速度脉动水平高于Nopert,这是由于Pert1、Pert2 和Nopert的剪切层在该区域处于不同的流动状态,这与2.2 节的现象一致,并且Pert2 喷流向湍流过渡早于Pert1,这是由于扰动涡分别从不同的流向位置开始破碎。当流动向下游发展,Pert1 和Pert2 的预测结果有不同程度的改善,均低于Nopert 预测的脉动水平,其中Pert1 的峰值水平最接近实验值。从图9 示出的脉动速度的径向分布也可以看出,虽然在喷口附近本文计算的脉动峰值低于实验测量值,但随着流动向下游进行,两种扰动工况的预测结果均有所改善,与测量的脉动水平相当。相对于参考文献[16]的LES 结果,本文两种扰动的加入,使喷流湍流特性更接近实验值。
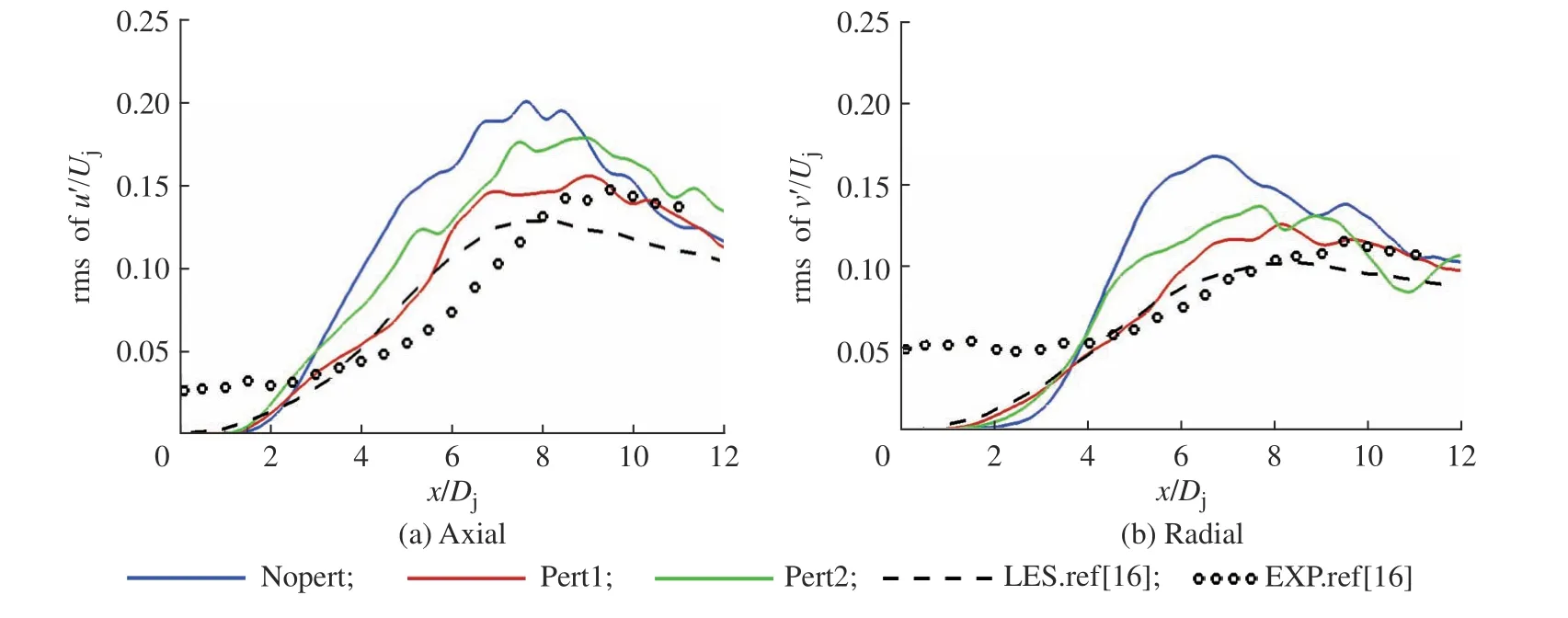
图8 中心线上脉动速度的均方根分布Fig. 8 Root mean square of fluctuating velocity distribution along centerline
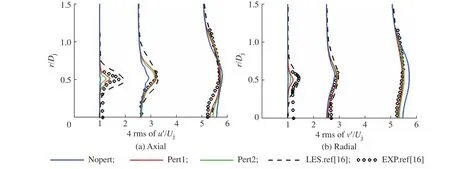
图9 脉动速度径向分布Fig. 9 Radial profiles of fluctuating velocity
轴向速度脉动和径向速度脉动沿唇线分布如图10(a)和10(b)所示。对比3 种工况,在唇线分布上同样可以观察到,其中Pert1 工况峰值水平最低。在靠近喷口区域x/Dj<2 ,Pert1 和Pert2 的速度脉动水平快速升高,且Pert2 脉动水平增长早于Pert1,而Nopert 在该区域发展缓慢,随后在x/Dj>2 的流域开始快速增长,Zhu 等[19]提出这是层流剪切层产生的自然现象。势流核末端及其下游区域,扰动工况的径向速度脉动低于无扰动工况,而轴向速度脉动区别较小。两条流向线上的预测结果表明,施加的扰动能够触发出逼近实际喷嘴出口的湍流水平,并且降低下游的脉动水平,改善流动发展的计算准确性。

图10 唇线上脉动速度均方根分布Fig. 10 Root mean square of fluctuating velocity distribution along lip line
2.3.2 谱密度(PSD)分布 高频声源位于中心线速度开始衰减的位置,低频声源位于势流核末端下游[20],因此选取了唇线上x/Dj为2.5、5、10 这3 个流向位置,分析速度脉动谱密度PSD。图11 和12 分别是唇线上轴向脉动和径向脉动的PSD 图。在流向位置x/Dj=2.5 处,Nopert 工况中轴向和径向速度脉动的峰值量纲为一的频率f D/Uj为0.6 左右,接近线性不稳定性理论中f Dj/Uj=0.68 ,该频率下的入口剪切层处于最不稳定轴对称模态,这代表了不稳定波的发展[21],造成与理论有差距的原因可能是非线性效应。随着流动向下游进行,脉动峰值逐渐向低频移动,这与喷射流动中两种不稳定模态有关,剪切层模态主导喷口区域,由剪切层涡卷曲的高频振荡引起。下游则受喷流优先模态控制,与低频的大尺度湍流结构的发展有关[22]。加入扰动后,在x/Dj=2.5 位置,Pert1 和Pert2 的PSD幅值在频率f Dj/Uj≈0.6 处变化不大,但其他在频段上均升高,因此与来流无扰动对比,扰动工况下的频谱没有明显的峰值,全频段的脉动水平都有所增强,说明Nopert 中的峰值可能与层流流动中的涡配对有关,而两种扰动加入以后,快速转捩得到的流动接近自然湍流,因此呈现出明显的多尺度特征,频谱表现为宽频特性。在势流核末端x/Dj=5 处,3 种工况下的PSD 趋于一致;而下游x/Dj=10的流向位置,Pert1 和Pert2 的PSD 在整个频段上都低于Nopert,与2.3.1 节中脉动沿轴向分布结果一致,快速转捩使得扰动工况的速度脉动峰值以及下游的脉动水平下降,频谱分析也进一步表明扰动能促使喷流在近喷口区域快速转捩以及在下游湍流发展。

图11 唇线上轴向脉动的谱密度Fig. 11 PSD of axial velocity fluctuation along lip line

图12 唇线上径向脉动的谱密度Fig. 12 PSD of radial velocity fluctuation along lip line
3 远声场
3.1 总声压级(OASPL)
图13 和图14 分别示出了r=30Dj和r=50Dj两圆面的OASPL 沿测角θ的分布。对比计算与实验结果,可以看出Nopert 的OASPL 高于测量结果5~10 dB,加入扰动后,与实验吻合程度明显改善。表明无扰动工况涡配对导致转捩的附加噪声引起很大误差,而采用扰动促成快速转捩,可以有效地消除这种误差。在r=30Dj的圆面上,Pert1 在θ为30°~110°的预测优于Pert2,而在θ为110°~150°时,Pert2 更接近实验值。而在更远位置r=50Dj,两种扰动工况预测相当。因此两种扰动虽有细微差别,但都能够大幅度地改善无扰动对声场计算造成的误差。
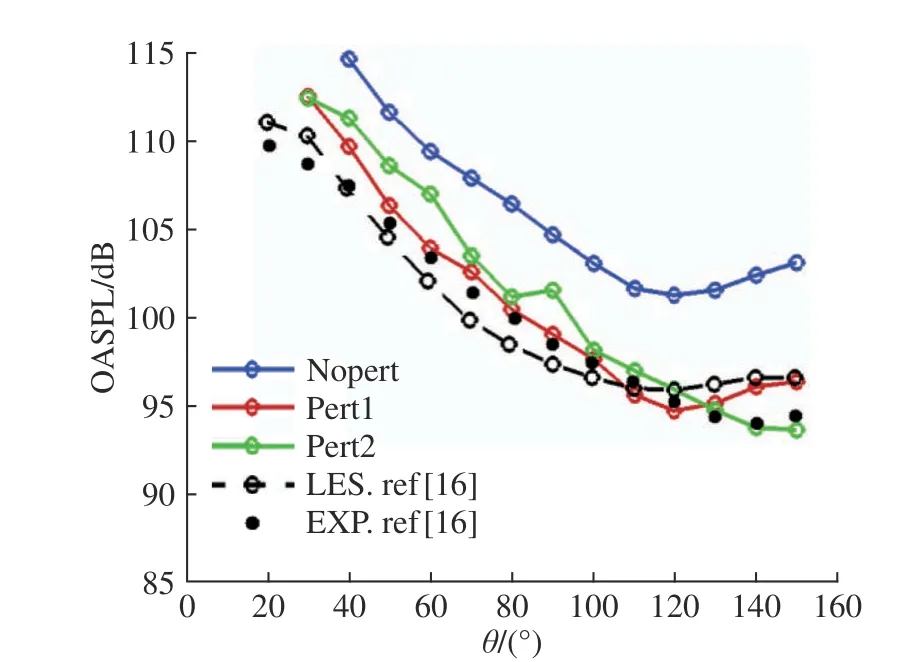
图13 远场r=30Dj 测点总声压级Fig. 13 OASPL at far-field r=30Dj

图14 远场r=50Dj 测点总声压级Fig. 14 OASPL at far-field r=50Dj
3.2 频谱特性
为了进一步研究扰动对声场预测的影响,测角选取了60°、100°和140°这3 个角度进行频谱特性分析。图15 和图16 分别示出了r=30Dj和r=50Dj两圆面上的声压级(SPL)频谱图。与实验结果对比发现,Nopert 的SPL 在低频段(f Dj/Uj<1 )高于实验结果,而高频段(f Dj/Uj>1 )低于实验结果,由于低频大尺度湍流噪声是总声场主要贡献者,其中就包括了涡配对带来的附加噪声误差,因此在前面总声压级分布中,Nopert 的预测高于实验值。相对于Nopert,随着扰动的加入,Pert1 和Pert2 的高频噪声有所升高,但低频噪声的降低有效地使整体噪声减弱,也证明了亚音速喷流中低频噪声占优势的地位。此外,Pert1和Pert2 的高频SPL 与实验仍有较大的视觉误差,可能是计算网格对最小尺度湍流结构的分辨仍然不是很充分而引起的。
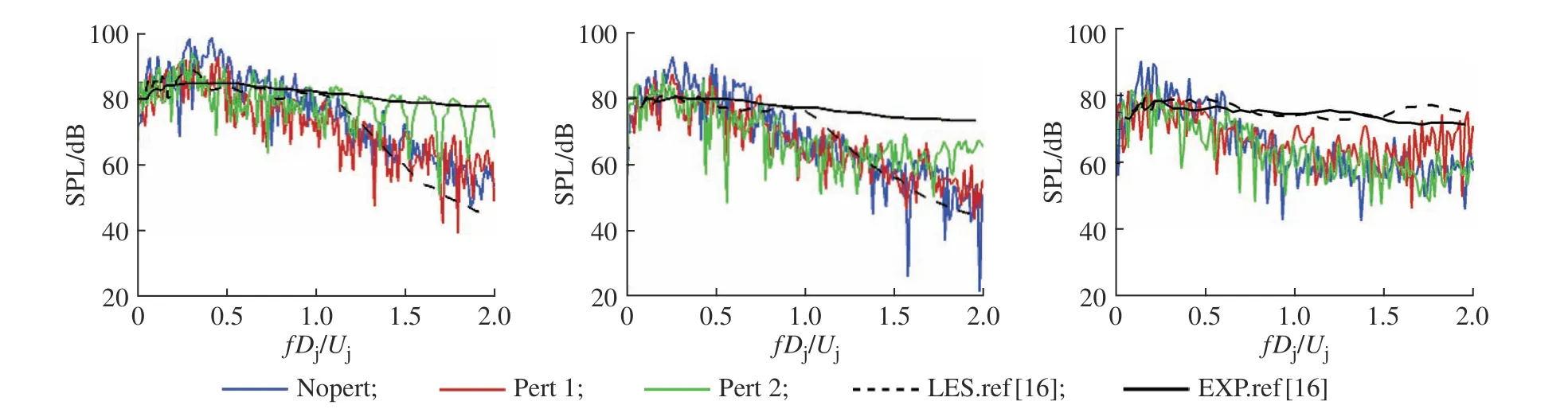
图15 远场r=30Dj 声压级频谱图Fig. 15 Spectra of SPL at far-field r=30Dj

图16 远场r=50Dj 声压级频谱图Fig. 16 Spectra of SPL at far-field r=50Dj
4 结 论
(1)触发喷口流动的快速转捩,使之接近实际的湍流来流,是喷流大涡模拟的一个关键。本文改进的多模态线性不稳定性扰动和涡环扰动都成功达到了这一效果。
(2)来流快速转捩的实现,有效地消除了无扰动时涡配对造成的声场误差,改善了湍流喷流远声场的预测结果。
(3)本文改进的多模态线性不稳定扰动方法,克服了涡环扰动湍流起始位置须人为移动的缺点。多模态的加入,更符合湍流来流的多尺度特性,体现了湍流频谱的宽频特征。

