双列圆锥滚子轴承内圈端面间隙偏差对其力学特性的影响*

温保岗 王家玉 杨 磊 王美令 康乃正

（1.大连工业大学机械工程与自动化学院;2.大连交通大学机车车辆工程学院;3.浙江兆丰机电股份有限公司）

0 引言

双列圆锥滚子轴承的内外圈均具有锥形滚道，且内圈为分体式结构的一对圆锥滚子轴承，能承受较大径向负荷和双向轴向负荷，广泛应用在轨道车辆轴承、风电主轴、驱动桥主减速等领域。双列圆锥滚子轴承内圈为分体式结构，设计加工过程中，两内圈滚道直径与锥角尺寸难免存在偏差，使得内圈端面间存在间隙，间隙存在偏差。在承受外载荷作用时，内圈间隙使得滚动体载荷分配等产生变化，直接影响轴承内部接触力学和整体刚度特性。因此，开展双列圆锥滚子轴承内圈端面间隙对其力学性能影响具有重要的研究意义和工程实用价值。

国内外学者对圆锥滚子轴承接触力学和刚度特性展开较为系统且大量的研究。Bercea[1]运用了拟静力学的研究方法，建立了双列圆锥滚子轴承力学模型。分析了不同外载荷对轴承接触载荷及刚度的影响；罗继伟[2]建立了轴承内部的接触应力数值求解计算模型。得到双列圆锥滚子轴承的载荷分布规律及接触应力大小；王彦伟[3]使用切片方法对单个滚子滚道接触进行数值计算，并以此为基础对圆锥滚子轴承进行总体接触受力和变形分析。根据变形协调和力平衡条件，建立了圆锥滚子轴承接触分析的数学模型；Creţu S[4]研究了圆锥滚子轴承在承受不同的轴向载荷和不同转速工况下轴承内部的载荷分布规律。吴昊[5]推导了考虑油膜厚度的圆锥滚子轴承径向刚度计算公式；张敬东[6]分析了车辆变速器在不同档位状态下圆锥滚子轴承滚动体与内、外圈的接触应力值。Tong[7]等基于分部积分法建立单列圆锥滚子轴承力学模型，分析径向载荷和力矩载荷的力学特征。Zhang HW[8]开展了圆锥滚子轴承对数型滚动体不同曲率下的接触应力变化规律。H.Wu[9]给出了润滑油油膜影响的圆锥滚子轴承综合刚度数值计算模型。上述研究主要分析了外载荷或轴承主结构参数对圆锥滚子轴承力学特性的影响，而均未针对内圈分体式结构双列圆锥轴承内圈端面间隙偏差对力学特性的影响进行分析，内圈端面间隙偏差如何设计和控制尚不明确。

针对双列圆锥滚子轴承内圈端面间隙引起的力学性能变化问题，本文以某型双列圆锥滚子轴承为研究对象，基于有限元方法建立具有内圈端面间隙的双列圆锥滚子轴承有限元模型，分析不同载荷作用下内圈间隙偏差对其接触力学和刚度特性的影响。

1 考虑内圈端面间隙的双列圆锥滚子轴承力学建模

1.1 双列圆锥滚子轴承有限元模型

双列圆锥滚子轴承外圈为一体，内圈为左右分体式结构。由于内圈、滚子以及外圈制造偏差使两内圈两端面间存在间隙，称之为端面间隙，下文简称内圈间隙，具体表示为dδ，轴承主结构参数见图1和表1所示。

图1 双列圆锥滚子轴承结构示意图Fig.1 Structural diagram of double row tapered roller bearing

表1 双列圆锥滚子轴承结构尺寸Tab.1 Structural dimensions of double row tapered roller bearings

轴承材料为GCr15，根据表1 轴承结构尺寸参数建立双列圆锥滚子轴承三维模型，建模需对轴承进行简化，忽略倒角、凹槽及保持架等结构特征，此外，内圈端面间存在间隙，具体三维模型如图2所示。

图2 双列圆锥滚子轴承三维模型Fig.2 Three dimensional model of double row tapered roller bearing

双列圆锥滚子轴承单元类型选用Solid45，采用扫略网格划分，最小网格尺寸为1mm，有限元模型中共包含网格数187445，节点数193405，具体网格划分如图3所示。

图3 双列圆锥滚子轴承模型网格划分Fig.3 Mesh generation of double row tapered roller bearing model

接触对设置单元选用CONTA174 和目标单元TARGE170来定义，具体如图4所示。

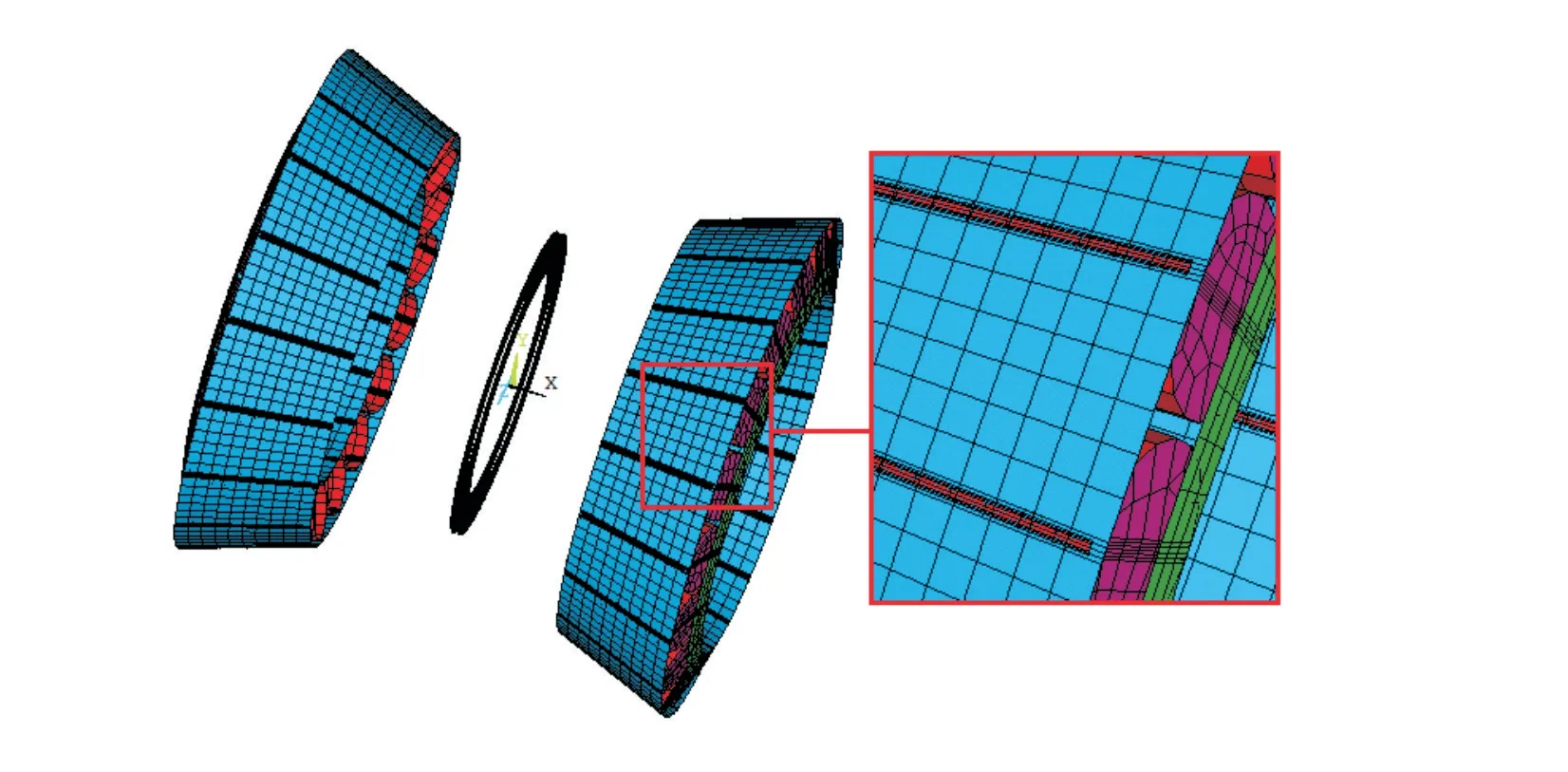
图4 双列圆锥滚子轴承接触对Fig.4 Contact pairs of double row tapered roller bearings

考虑工作和装配影响，轴承外圈固定，约束外圈外表面节点的全自由度；内圈旋转，约束内圈节点z方向的转动自由度；此外，约束滚子节点的周向自由度，内圈内表面施加载荷，具体如图5所示。

图5 轴承约束及载荷施加示意图Fig.5 Schematic diagram of bearing restraint and load application

轴承径向刚度计算公式为

式中，ΔFr表示轴承径向载荷变化量；Δδr表示轴承内圈中心径向位移的变化量，通过有限元内圈的位移点获取。

1.2 圆锥滚子轴承接触应力

滚子轴承接触符合赫兹线接触假设，在外载荷Qmax的作用下，滚子与内外圈滚道发生接触，接触处滚子有效长度l，负荷线密度q，其中q=Qmax/L，接触界面为宽2b、长度L的矩形，在区间[-b，b]内，接触应力沿着接触区域呈椭圆分布，表示为

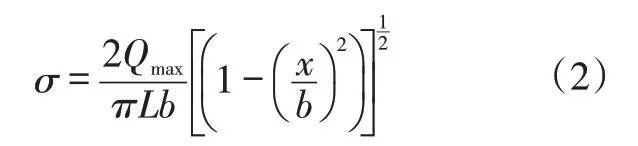
最大接触应力为

接触半宽为

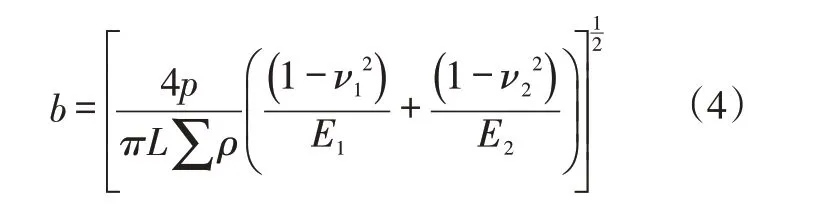
式中，∑ρ为轴承主曲率函数、F(ρ)为主曲率差函数，具体计算参考文献[10]。

1.3 模型对比验证

双列圆锥滚子轴承内圈间隙为0mm，径向载荷14000N、轴向载荷7000N 作用下右侧滚子与内外圈接触应力如图6所示。从图中可以看出，双列圆锥滚子轴承滚动体与滚道随着位置角度呈三角函数变化，且有限元与理论计算结果有较好的吻合性，变化趋势基本一致，验证了模型的准确性，其中理论计算值略高于有限元计算值，主要是由于解析计算内外圈假设为刚性套圈，有限元模型套圈为柔性体。

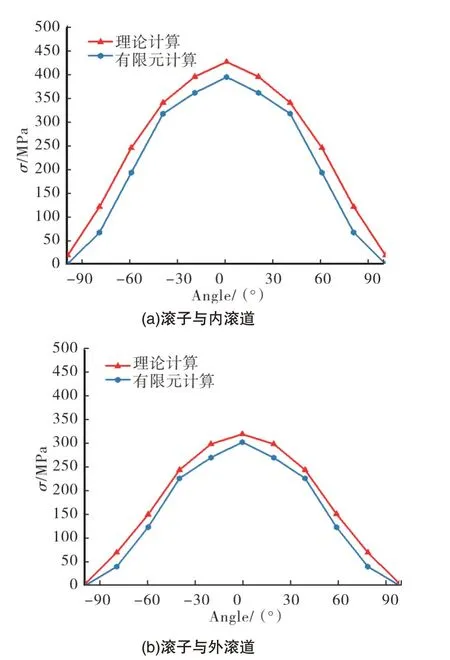
图6 右侧滚子与滚道的接触应力Fig.6 Contact stress between right roller and raceway

2 内圈间隙偏差对双列圆锥滚子轴承力学特性的影响

为了研究不同载荷下的内圈间隙的轴承力学性能变化，分别开展对轴承接触力学性能和轴承刚度特性的影响分析。有限元模型中不考虑转速影响，内外圈滚道接触应力变化一致，下文以内圈滚动与滚子的接触为例进行分析，具体工况如表2所示。

表2 工况参数Tab.2 Working condition parameters

2.1 内圈间隙偏差对轴承接触力学性能影响

轴向载荷7000N，径向载荷分别为14000N、15000N、16000N 条件下（工况一）的轴承接触应力随内圈间隙变化如图7所示。从图中可以看出：径向载荷一定时，内圈间隙增加会使得左右两侧滚子与滚道之间接触应力增大，而两内圈端面之间接触应力减小。间隙0.05mm以上时，接触应力变化不明显，这是由于在内圈间隙较小时，当轴承承载时，两内圈端面存在较大的相互的作用力，而随着间隙增加，两内圈端面作用逐渐减小，原来由内外圈端面承受的轴向载荷将由滚子与滚道承受，导致滚子与内外圈滚道间的接触应力增加。此外，径向载荷增加将引起左右两侧滚子与内圈滚道的接触应力增大，两内圈端面之间应力减小，这是由于增加径向载荷使轴向载荷的轴向分量减小，进而减小两轴承内圈的接触应力。

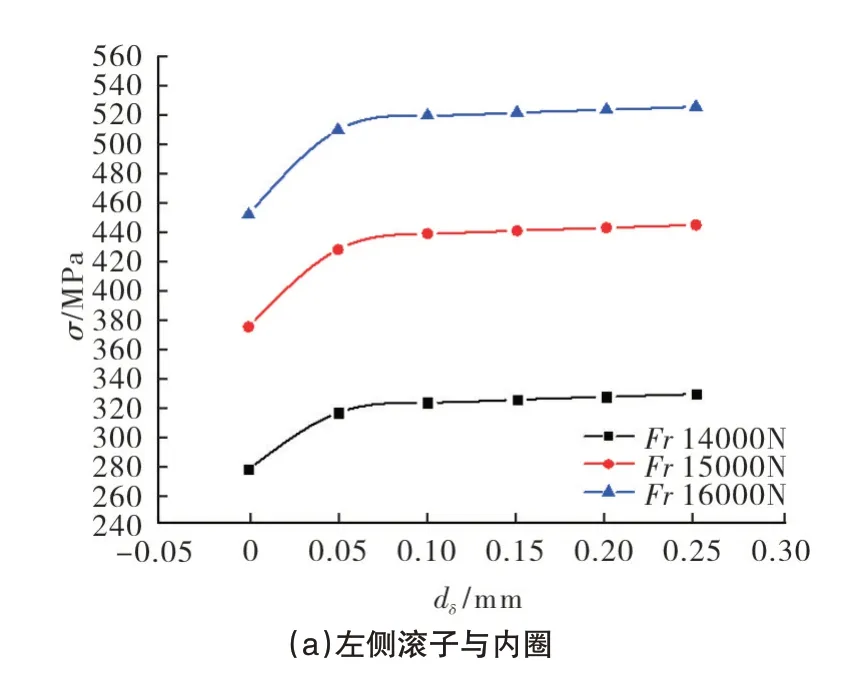
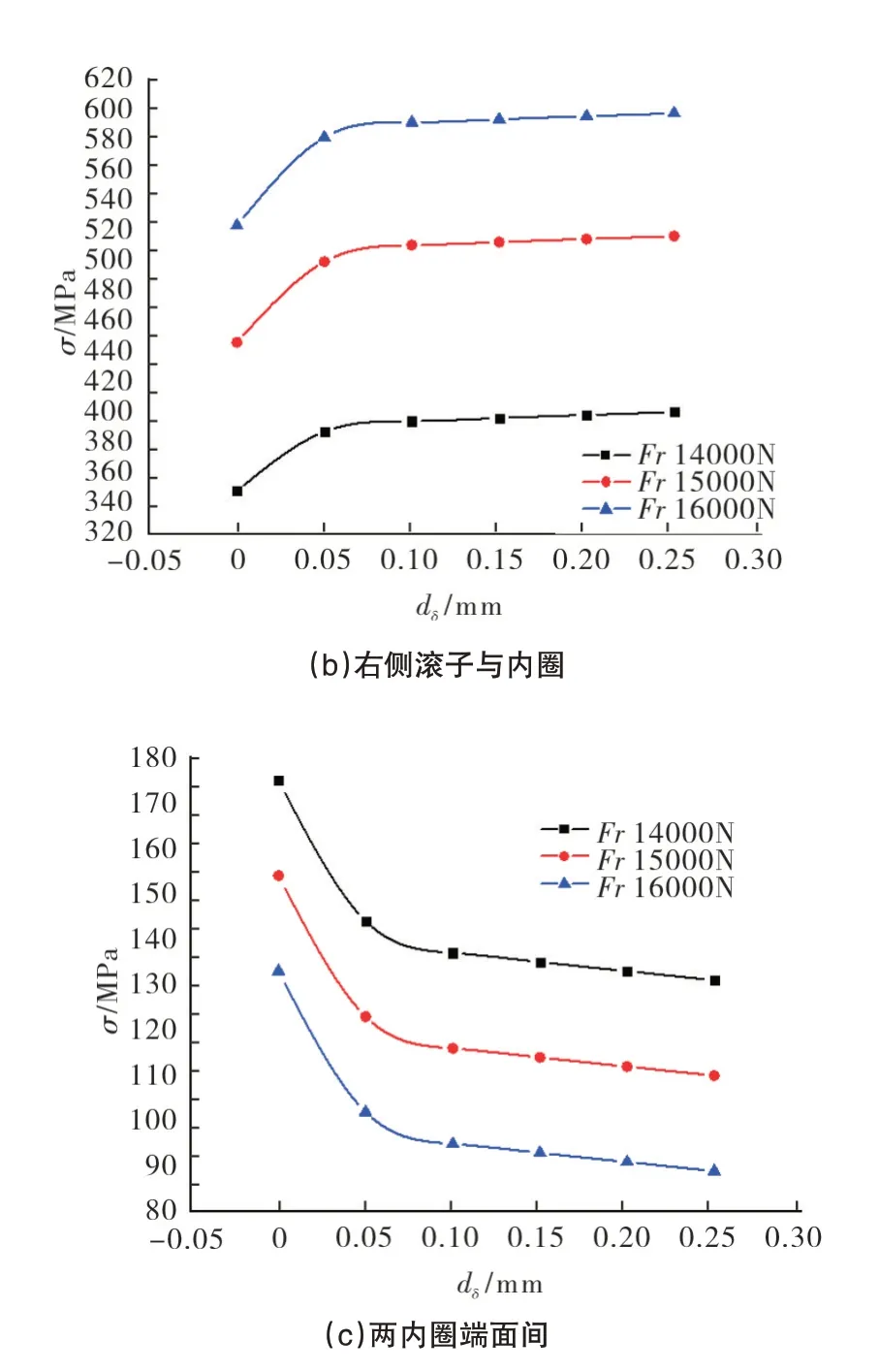
图7 不同径向载荷接触应力随内圈间隙变化Fig.7 Variation of contact stress with inner ring clearance under different radial loads

径向载荷14000N，轴向载荷分别为7000N、8000N、9000N 条件下（工况二）轴承接触应力随内圈间隙变化如图8 所示。从图中可以看出：内圈间隙一定时，轴向载荷的增加将会引起左右两侧滚子和内圈滚道以及两内圈端面之间的接触应力增大，且两侧滚子与内圈的变化速率存在较大差异，这是由于轴承滚子与滚道的轴向分量和内圈端面用来承受轴向载荷作用，轴向载荷的增加将致使滚子与滚道以及内圈端面的作用力增加，进而导致轴承接触应力增加。

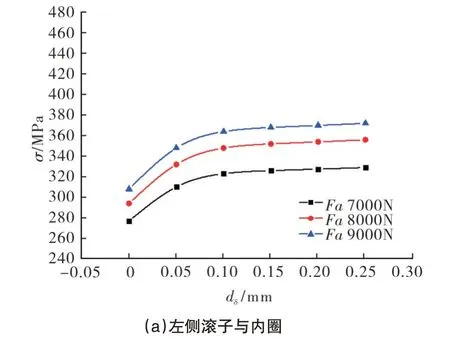
图8 不同轴向载荷下接触应力随内圈间隙变化Fig.8 Variation of contact stress with inner ring clearance under different axial loads

2.2 内圈间隙偏差对轴承刚度特性影响

工况一、工况二条件下，轴承径向刚度随内圈间隙变化分别如图9 所示。从图可以看出：随内圈间隙增加，轴承刚度略微增大，间隙增加到0.05mm 以上时，刚度变化不明显，这是由于随着内圈间隙变化，滚子与滚道以及内圈端面承载发生改变，滚子与滚道承载增加（见图7 和8），接触刚度增加所致。此外，随着轴向载荷、径向载荷的增加，轴承的刚度也增加，符合轴承刚度的变化规律，进一步验证模型准确。

图9 轴承刚度随内圈间隙变化Fig.9 The bearing stiffness varies with the inner ring clearance

3 结论

本文建立了考虑内圈端面间隙的双列圆锥滚子轴承的力学模型，研究了内圈间隙偏差对该轴承力学特性的影响，得到如下结论：

1）建立了双列圆锥滚子轴承有限元力学模型，并与赫兹接触理论计算结果进行对比，验证了模型准确性。

2）轴承内圈间隙变化会引起双列圆锥滚子轴承滚动体与滚道和内圈端面接触应力以及轴承刚度的变化，因此在设计与制造过程中需要对间隙进行控制。

3）随着轴承内圈间隙增加，双列圆锥滚子轴承的滚子与滚道间接触应力增大，两内圈端面之间应力减小，轴承刚度增加；轴承间隙增加到一定值后（0.05mm），轴承的内部接触应力和轴承刚度变化将不明显，以此作为端面间隙的控制范围。