用于风电场群规划的风电场尺度尾流模型研究*

王 鹏 刘建平 李大伟 孟 航 余 鑫

(1.中国三峡新能源（集团）股份有限公司；2.华北电力大学新能源学院）

1 概述

随着风电产业发展，风电机组单机容量与风电场占地面积都在逐渐增大。在建成风电基地中，风电场的尾流最长可以延伸至数十公里，周边上游风电场产生的尾流效应会对下游风电场发电量产生显著影响[1，2]。

下游大部分风电机组处于上游机组的尾流中，相比于来流，尾流区风速降低，湍流强度增加[3-6]，导致下游风电机组发电量损失为10%～20%[7]。在过去的研究中，通过构建不同的单台机组尾流模型来研究风电机组的尾流特性。Lissman[8]将Abramovitch 射流理论应用于尾流建模，提出了单台风电机组MILLY 半经验尾流模型。Jensen[9-10]基于理想流体力学的质量守恒方程，认为尾流区截面上各处速度相等，提出Jensen 尾流模型，该模型具有较强鲁棒性，在风资源计算软件中广泛应用。Frandsen[11]根据动量守恒定理提出了Frandsen尾流模型，该模型在尾流区假设的速度分布与Jensen尾流模型相同。文献[12-14]基于能量守恒和高斯分布函数发展了二维Jensen 尾流模型。Bastankhah[15]采用动量定理和高斯分布函数发展了Frandsen 尾流模型的二维形式，在学术研究中得到了广泛应用。然而，以往尾流研究关注风电机组尺度，目前缺少对风电场尺度尾流效应的相关研究。风电场尺度尾流对局地平均风速有较大影响。文献[1]在中国新疆哈密的风电场研究也发现，上游风电场对下游邻近风电场年平均风速有着较大影响，在盛行风向和年平均风速下，全场尾流一般在下游16.5km处恢复。此外，由于上游风电场的影响，下游风电场的尾流距离加倍。文献[16]发现风电场运行对局地边界层气象因素有一定影响。文献[17]通过大涡模拟方法模拟大型风电场，结果表明在风电场下游10km 处风速为来流风速的90%左右。文献[18]基于CFD方法提出了类Jensen风电场尾流模型，但是对风电场尾流模型各参数未做进一步探究。

上述研究使风电机组尾流模型得到了比较全面的完善，但是对风电场尺度尾流效应的研究却较少。风电大基地建设是目前风电发展的趋势，例如我国正在建设中的如乌兰察布，酒泉风电等风电基地，尾流效应问题对大基地的规划提出了新的要求。为了解决这一问题，本研究将对风电场尾流区流向平均风速变化规律展开研究。首先，通过模拟风电场尾流，探究风电场下游风速分布规律并提出类Jensen风电场尾流模型；然后，探究风电场尾流平均风速变化与湍流强度及风电机组排布疏密度的关系，并提出关于风电场阻滞参数和湍流效应参数的双参数风电场尾流模型；最后，根据我国西北某风电基地风电场的实测数据分析风电场间尾流效应，对所提风电场尾流模型进行验证。所提风电场模型模拟结果与实测结果相符合，能够较好地表达风电场尾流平均风速的变化规律，对未来大型风电基地宏观规划有指导意义。技术路线如图1所示。

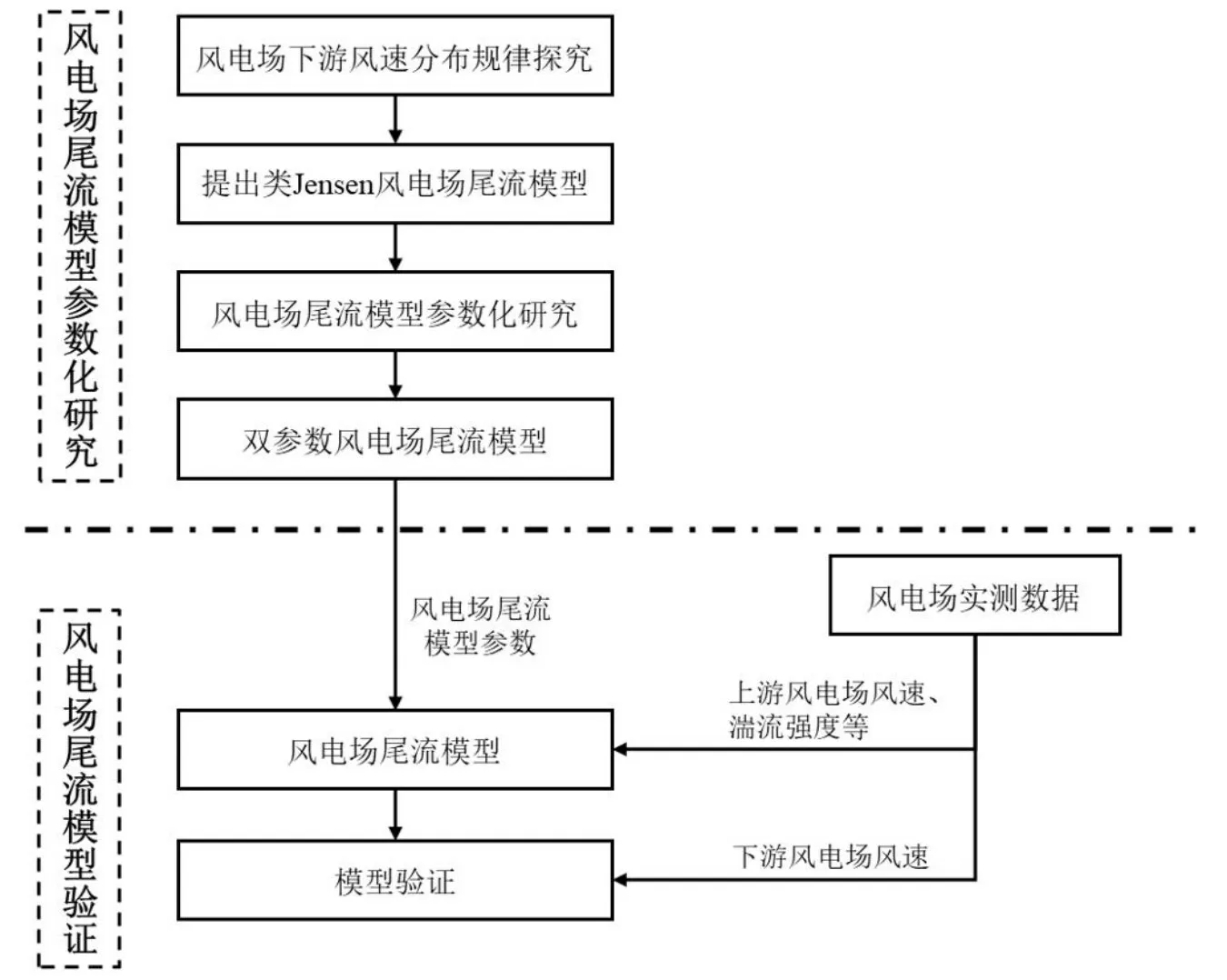
图1 本文技术路线Fig.1 The technical route of this paper

2 风电场尾流探究

风电场尾流的探究将以整个风电场尾流区为研究对象，探究风电场尾流区流向平均风速的发展变化。本节根据模拟的风电场尾流风速分布特征，探究风电场尾流平均风速变化与湍流强度及风电场疏密度的关系，最终建立风电场半经验尾流数学模型。

2.1 风电场尾流区风速

本文构建32 台风电机组的理想风电场（风轮直径126m，轮毂高度90m），风电机组横向间距为7D，纵向间距为5D，布局形式如图2 所示。使用工程尾流模型模拟风电机组尾流，其中尾流速度模型采用BPA 尾流模型[15]，其基于轴对称、自相似高斯分布的尾流速度亏损假设，根据质量和动量守恒，忽略动量方程中的粘性和压力项发展的二维尾流解析模型，在工程中得到广泛的应用。尾流叠加区域采用平方和叠加模型计算尾流速度[19]。设置入流风速为9m/s，风向为270°，环境湍流强度为6%。对风电场下游轮毂高度处风速采样，风速分布如图3(a)所示。随着与风电场距离的增加风速逐渐恢复，在下游4km处风速分布呈现“顶帽”形状。风电场下游轮毂高度处流向平均风速分布如图3(b)所示（Uwf为风电场尾流区流向平均风速，U∞为来流风速），风电场下游1～2km范围内，Uwf逐渐恢复；在风电场下游2km处，Uwf恢复至8.5m/s 左右；在风电场下游2km 外，随距离增加，Uwf增长速率减缓。

图2 风电场布局Fig.2 Layout of wind farm

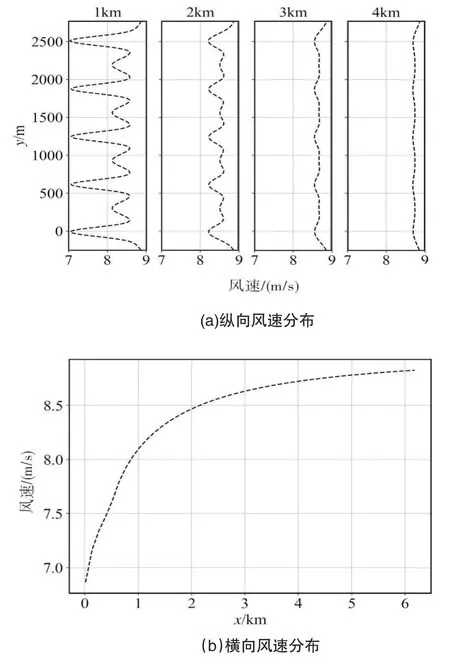
图3 风电场尾流区轮毂高度处风速分布Fig.3 Wind speed distribution at the hub height in the wake region of a wind farm

2.2 风电场半经验尾流数学模型

如图3(a)所示，风电场尾流向下游发展一定距离后风速分布呈现“顶帽”形状，与Jensen尾流模型水平方向上假设的速度分布相似。图3(b)所示的风电场尾流区流向平均风速变化规律与Jensen 尾流模型描述的流向尾流速度分布规律相似。因此，风电场尾流区流向风速的变化特征可通过类似于Jensen 尾流模型的形式描述，Jensen 尾流模型表达式如式（1）。根据Jensen 尾流模型引入风电场阻滞参数Cwf，表示风电场对来流风的推力作用，其影响风电场下游的风速下降的程度；引入湍流效应参数，表示风电场尾流的扩张程度，影响风电场尺度尾流恢复。因此，风电场半经验尾流数学模型（以下简称：风电场尾流模型）表达式如式（2）所示。

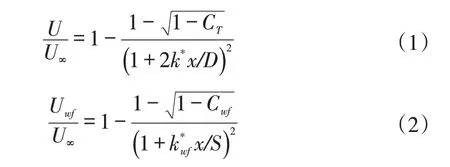
式中，k*为尾流扩张系数；CT为风电机组推力系数；D为风轮直径；Uwf为风电场下游x位置处的尾流平均风速；Cwf为风电场阻滞参数；为湍流效应参数；S为风电场纵向宽度。

2.3 风电场尾流数学模型参数化研究

在风电场中，湍流影响尾流的恢复，当湍流强度越大时，促使尾流与自由流的混合更剧烈，使得尾流风速恢复得更快[20]。另一方面，风电场中风电机组排布的疏密度也会影响风电场尾流的大小，当风电场中风电机组布置的越密集，风电场尾流就越严重。本小节将通过分析湍流强度和风电场疏密度对风电场尾流区风速的变化规律，讨论湍流强度和风电场疏密度与风电场尾流模型阻滞参数Cwf和湍流效应参数的关系。

本文中以风电场内风电机组风轮扫掠面积之和与风电场面积的比值来量化风电场疏密度，风电场机组布置的越密集,则疏密度越大。计算方法如式(3)：

式中，为电场疏密度；Dt为第t台机组风轮直径；T为风电场机组数量；A为风电场面积。

模拟不同湍流强度下和不同风电场疏密度下的风电场流场，采样风电场下游多个位置轮毂高度处平均风速，得到风电场下游轮毂高度处平均风速变化率与风电场下游距离的关系。通过非线性拟合得到风电场阻滞参数Cwf和湍流效应参数。其中设置入流风速为9m/s，风向为270°，湍流强度自4%到9%每次递增1%，共6 种情况，疏密度分别为0.052，0.042，0.035 和0.03共4种情况。

湍流强度为6%时不同疏密度风电场下游流向平均风速变化率如图4所示。当风电场机组布置的越稀疏，疏密度减小，湍流效应参数随之减小同时风电场阻滞参数Cwf随疏密度的减小而增加。

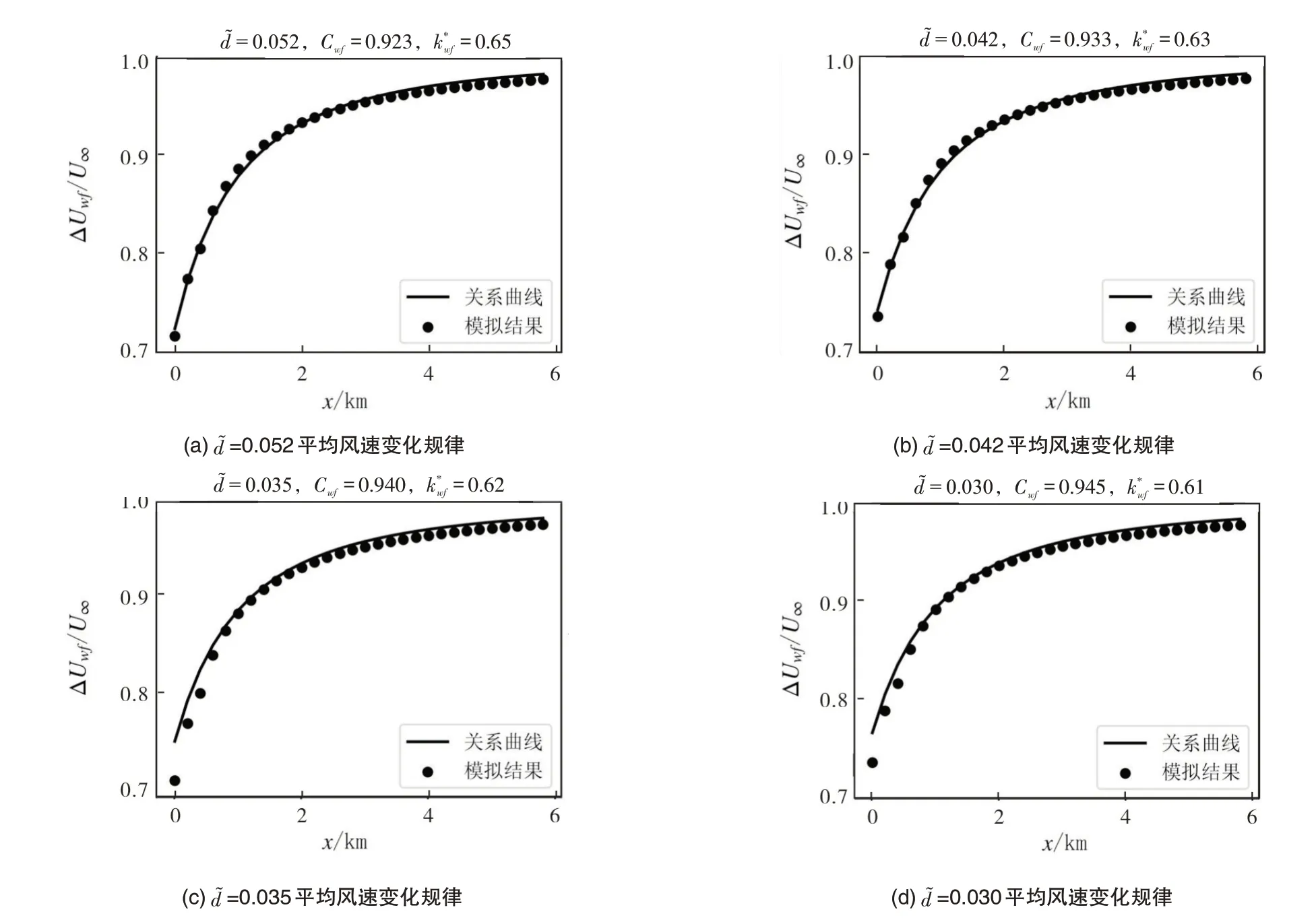
图4 不同疏密度下的风电场下游流向平均风速变化规律Fig.4 Variation of mean wind speed in downstream direction of wind farms with different densities

分别模拟上述24 种工况，模拟结果如图5 所示。图5(a)显示风电场阻滞参数Cwf受到风电场疏密度和湍流强度TI 的协同影响，风电场阻滞参数Cwf与风电场疏密度线性相关，关系曲线斜率随湍流强度TI变化，与纵轴的几乎一致，可认为其截距相等。因此，风电场阻滞参数Cwf与疏密度关系可以通过式(4)来描述，通过线性拟合得到参数kd=-8.26，ε=3.29，b=0.331。

图5 风电场疏密度与湍流强度对风电场模型参数影响规律Fig.5 The influence law of wind farm density and turbulence intensity on the parameters of wind farm model

式中，kd，ε，b为经验参数；TI为湍流强度。

图5(b)显示湍流强度TI和风电场疏密度对湍流效应参数的协同影响，湍流效应参数与湍流强度TI线性相关，其相关关系受疏密度影响较小。因此，湍流效应参数与湍流强度TI关系可以通过式(5)来描述，通过线性拟合得到参数kti=5.175，δ=0.314。

式中，kti，δ为经验参数。

根据式(2)、式(4)和式(5)，风电场半经验尾流数学模型表达式如式(6)：

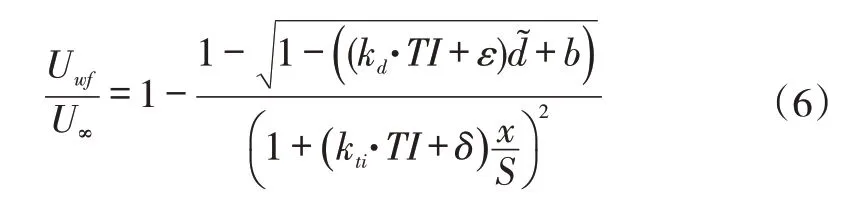
3 算例分析

在我国西北地区由于风资源丰富，且主导风向单一，沿主导风向排布众多风电场，位于下游前期建设的风电场将受到上游风电场的尾流影响。本节首先根据我国西北某风电基地中两座风电场实测数据，分析主导风向下风电场间尾流效应。然后，基于实测数据验证本文提出的风电场尾流模型。

3.1 基于实测数据风电场间尾流效应分析

该基地主导风向为西北风和东南风，由B1、B5 和B4 风电场构成风电场群局部，基本布局形式和主导风向如图6所示。当风向为120°和300°左右时，机组间距较大，场内尾流损失较小，风电场间尾流影响最显著。因此，对B1风电场和B4风电场的测风塔数据和SCADA数据进行数据清洗后，筛选上游风电场轮毂高度处入流风速大于4m/s，平均风向为120°或300°的风况（数据分辨率为10min，采样时长为4h）得到4个代表时段风速时间序列（其中代表时段1 平均风向为300°，其余代表时段平均风向为120°）。如图7 所示，代表时段的风速时间序列反映出了风电场尾流从上游风电场传递到下游的时移特性，此外，上下游风电场风速的变化趋势基本一致，存在显著的风速差。

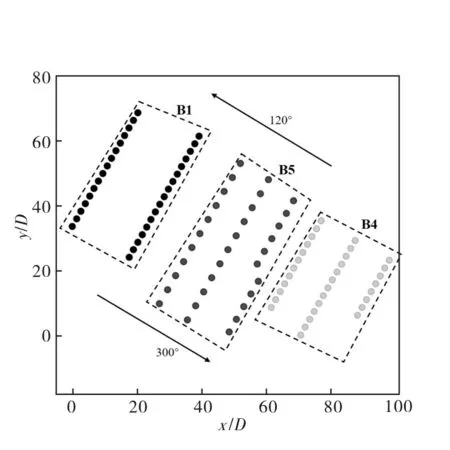
图6 风电场群布局Fig.6 Layout of wind farm clusters

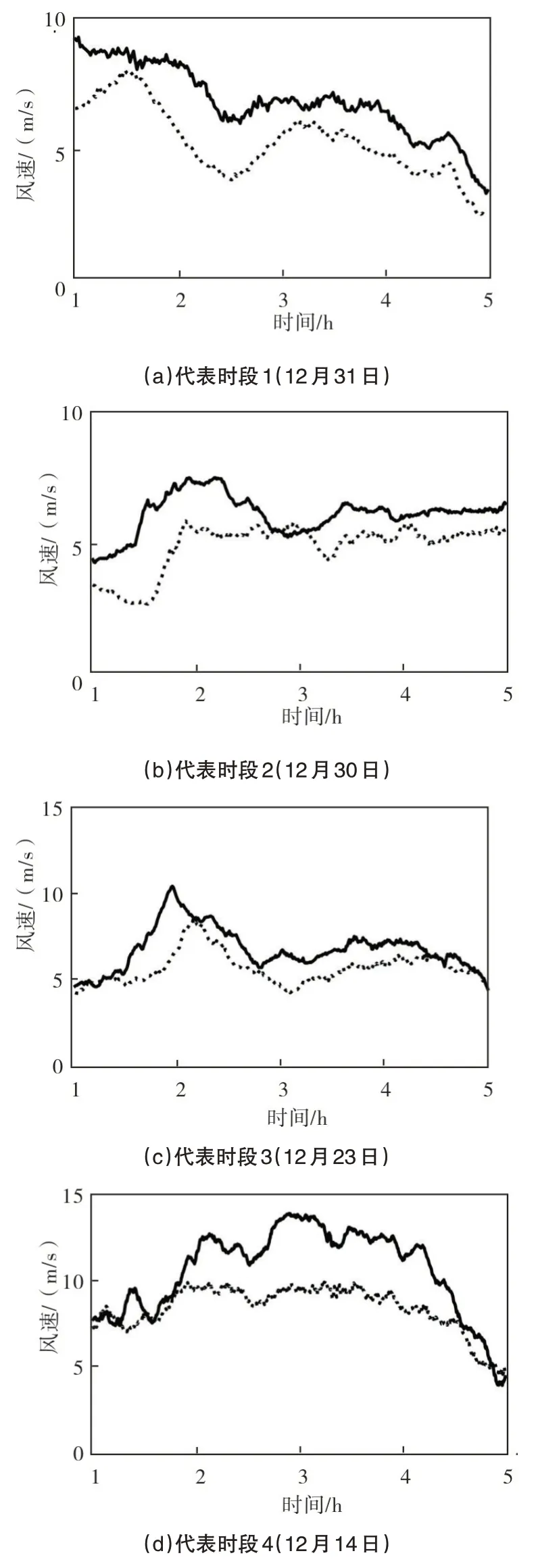
图7 不同代表时段上下游风电场风速波动比较Fig.7 Comparison of wind speed fluctuation of upstream and downstream wind farms in different representative periods

为进一步定量分析风电场间尾流效应，计算不同代表时段B1和B4风电场的时间段内的平均风速，通过上下游风电场平均风速的相对误差表示风电场间的尾流损失。计算公式如下式(7)。

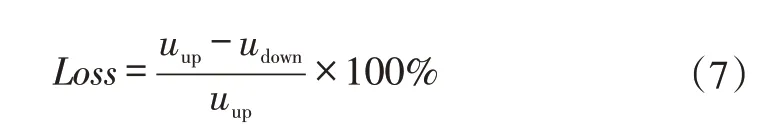
式中，Loss为风电场间尾流损失比率，uup为上游风电平均风速，udown为下游风电场平均风速。4 个代表时段的风电场平均风速和风电场间尾流损失如表1 所示。在主导风向下该风电场群上游两座风电场造成的尾流损失约为20%。相比于代表时段1，其他代表时段的平均尾流损失减小了4%。在代表时段1 风况下，风电场B4与风电场B5的流向间距较小，风电场B5的尾流效应对风电场B1 影响更显著；代表时段2，3 和4 风况下，风电场B1与风电场B5的流向间距较大，相较于代表时段1，风电场B5的尾流效应对风电场B4影响较小。

表1 不同代表时段的风电场风况和风电场间尾流效应造成的平均风速损失Tab.1 Wind conditions of wind farms in different representative periods and average wind speed loss caused by wake effects between wind farms

3.2 风电场尾流模型验证

本文通过风电场尾流模型模拟不同风况，计算下游风电场入流风速，并使用相对误差作为检验模型准确度的指标。相对误差的定义如下式(8)：

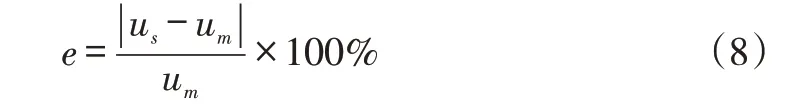
式中，e为相对误差；us为风电场尾流模型模拟结果；um为下游风电场实测结果。

为了简化计算过程，本文将表1中代表时段的平均风向和风电场平均风速作为该时段的代表风况。首先，根据平均风向确定风电场的相对位置，并计算风电场的宽度S，将上游风电场平均风速作为风电场尾流模型的入流风速U∞；然后，根据式(3)计算三座风电场的疏密度，并统计不同代表时段的湍流强度TI得到不同风况下的风电场参数，如表2 所示。最后，通过风电场尾流模型（模型参数如表3所示）与尾流叠加模型（在尾流叠加区域采用平方和叠加模型）计算出下游风电场的入流风速作为模拟结果。

根据表2 和表3 中的参数设定，对4 个代表时段风况进行模拟得到模拟结果，并根据式(8)计算模型的准确度。如表4 所示，4 个代表风况下风电场模拟结果均大于实测风速，低估了风电场尾流损失，但模拟结果的平均相对误差约为8.5%，其中代表时段3风况下模型误差最小仅为5.1%。因此，本文所提风电场尾流模型能够较好地表达风电场尾流平均风速变化规律。

表3 风电场尾流模型基本参数Tab.3 Basic parameters of wind farm wake model

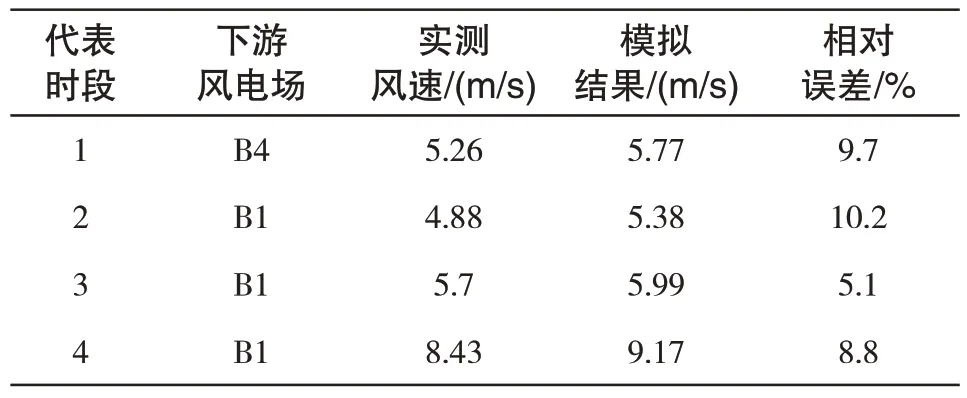
表4 不同风况下风电场尾流模型模拟结果与准确度Tab.4 Simulation results and accuracy of wind farm wake model under different wind conditions

4 结论

本研究首先通过模拟结果，揭示了风电场下游轮毂高度处流向风速变化规律，建立了双参数类Jensen风电场半经验尾流数学模型，揭示了风电场湍流强度和布机疏密度对模型参数的影响规律，基于实测数据对所提出的数学模型进行了验证。主要结论如下：

1）我国北方某风电基地实测数据表明：主导风向下，上游风电场尾流会造成下游风电场显著的平均风速损失（1～2m/s），损失比率约为15%～20%；

2）建立了风电场阻滞参数与湍流效应参数的双参数类Jensen 风电场尾流模型，通过模拟发现：a)湍流强度对湍流效应参数有显著的影响，当湍流强度越大时，风电场湍流效应参数越大；b)湍流强度与风电场疏密度协同影响风电场阻滞参数，当风电场中机组布置的越密集，风电场阻滞参数越大，但湍流强度越大时，风电场阻滞参数越小。

3）基于实测数据对所提风电场尾流模型进行验证，所提风电场模型模拟结果与实测结果的相对误差约为8.3%，能够较好地表达风电场尾流平均风速的变化规律，对未来大型风电基地宏观规划具有指导意义。

本文取得了一定研究成果，但还存在不足之处。本文中所提模型仅考虑平坦地形，对于复杂地形还需要进一步研究。此外，未来将结合风电场尾流区实测数据对风电场尾流模型做进一步探究。

致谢：本工作得到了中国长江三峡集团有限公司科研项目资助（合同编号：63010037）