内圈倾斜角对高速角接触球轴承动态特性的影响

常丽萍，常亚南，杨雷雷

(1.中车株洲电机有限公司，湖南 株洲 412000；2.洛阳轴承研究所有限公司，河南 洛阳 471000；3.长沙景嘉微电子股份有限公司，湖南 长沙 410000)

0 引言

角接触球轴承在武器装备、军用车辆等领域有着广泛应用，是关键零部件之一。随着对主机性能要求的不断提高，对与之配套的角接触球轴承性能要求也越来越高。实际工程中，由于加工装配误差和运转时轴的挠曲变形不可避免，导致轴承内外套圈发生相对倾斜[1]。若轴承内外圈之间存在倾斜角，则必将影响轴承动态性能，降低轴承旋转精度，从而影响轴承使用寿命，甚至造成轴承卡死，引起轴承早期失效[2]。

国外对套圈倾斜角接触球轴承的研究开始较早。Ellis[3]对球轴承套圈倾斜进行了研究，并论述了套圈倾斜产生的原因、可能的影响及倾斜故障的诊断方法，提出避免倾斜问题的经验性措施。Hinton[4-5]对航空发动机球轴承因保持架疲劳断裂而失效的案例进行了分析，通过大量实测统计数据发现套圈倾斜是主要原因之一。Crawford[6]对套圈倾斜状态下轴承保持架的应力进行测试，发现当套圈倾斜角从15.6′增加到36.6′时，轴承保持架的应力波动量从1.8 MPa增加到35.2 MPa，进一步证实了Hinton的结论。Ertas等[7]结合试验与计算机仿真研究了套圈倾斜对轴承径向刚度的影响，通过分析转子系统的特征频率与临界转速，发现套圈固定的倾斜角会增加轴承的径向刚度。Bugra等[8]通过实验测试和转子动力学计算机建模，给出了不同轴向载荷工况条件下套圈发生倾斜时的角接触球轴承径向刚度。Damian等[9]通过数值计算方法研究了内圈倾斜角对轴承载荷分布的影响。Oktaviana等[10]研究了内圈倾斜角对角接触球轴承打滑影响，发现在定位预紧下内圈倾斜角不会增大轴承打滑。张学宁等[11]研究了套圈倾斜角对轴承接触角的影响规律，发现套圈倾斜时接触角沿位置角分布不均，且这些现象随套圈倾斜角的增大而愈发明显。周阳[12]编制了考虑安装误差的角接触球轴承计算软件。熊万里等[13]研究了高速角接触球轴承套圈倾斜角允许范围，但其未考虑工况因素的影响。张进华等[14]和方斌等[15]研究了联合载荷作用下高速角接触球轴承快速计算方法并对接触角变化进行分析。尽管针对内圈倾斜角问题国内外学者开展了上述工作，但大多数学者的分析均假设轴承在单一工况下运行，没有涉及转速、轴向载荷、联合载荷及滚珠材料等应用条件改变时内圈倾斜角对轴承动态特性的影响分析。然而工程应用条件十分复杂，轴承在单一工况下运行的情况并不常见，且近年来氮化硅陶瓷滚动体轴承逐渐被广泛应用，因此迫切需要全面地研究不同工况条件下及滚动体材料为氮化硅陶瓷时内圈倾斜角对轴承动态特性的影响规律，为工程应用提供理论指导。

本文使用赫兹接触理论建立了一种综合考虑内圈倾斜角、高速离心效应的轴承分析计算模型，采用Newton-Raphson迭代法对模型求解，开发了适用于内圈倾斜条件的高速角接触球轴承动态性能分析软件。在此基础上，系统研究了复杂工况内圈倾斜角对轴承接触角、套圈最大接触应力(简称接触应力)、旋滚比、滚珠公转转速以及刚度的影响规律。

1 内圈倾斜球轴承建模理论与方法

1.1 几何分析

假定轴承外圈固定，随轴旋转的内圈可相对外圈移动。当内圈相对外圈倾斜时，轴承一般会同时承受轴向负荷、径向负荷和力矩，套圈不同位置处各组件之间的几何关系将发生变化。轴承滚珠角位置如图1所示。图1中，dm为轴承中径，轴承每个滚珠都对应1个编号，编号为j的滚珠位置角ψj=360(j-1)/Z，j≤Z，Z为滚珠数目。

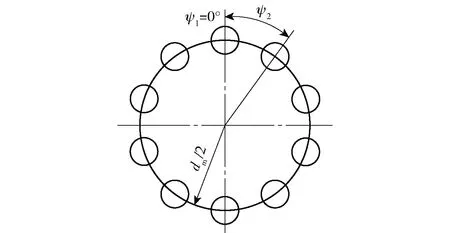
图1 滚珠角位置

图2为位置角ψj处，轴承运转前后套圈滚道沟曲率中心与球心相对位置的变化。图2中，δa表示轴向位移，δr表示径向位移，θ表示内圈倾斜角，A为外圈滚道沟曲率中心位置，保持固定不变，B点为球中心最初位置，B′为轴承运动平衡状态球中心最终位置，C点为内滚道沟曲率中心最初位置，C′点为轴承运动平衡状态内滚道沟曲率中心位置，α0为轴承初始接触角，αij和αej分别为轴承运动平衡状态滚珠内、外接触角，Aaj、Arj分别为轴承运动平衡状态内沟道曲率中心在轴向和径向的分量，Xaj、Xrj分别为轴承运动平衡状态球中心位置在轴向和径向的分量，Δij为内沟道曲率中心与球中心运转平衡位置之间的距离，Δej为外沟道曲率中心与球中心运转平衡位置之间的距离，Ri为内滚道沟曲率中心轨迹的半径，uc为轴承内圈的离心膨胀量，BD为轴承静止时内、外沟道曲率中心的距离。

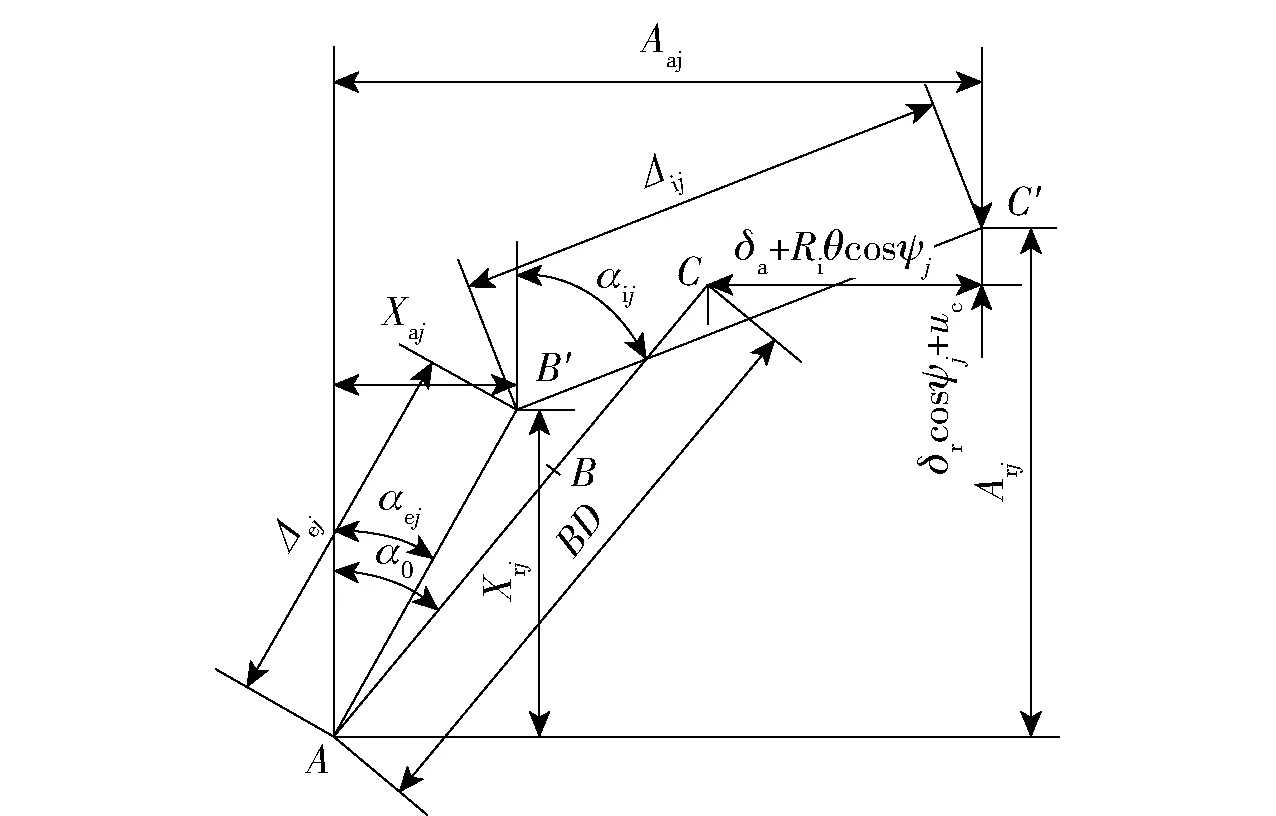
图2 滚珠j位移图

轴承内圈高速旋转产生离心膨胀，轴承内圈的离心膨胀量uc[16]表示为

(1)

式中:ρ为材料密度；ω为转速；E为材料杨氏模量；d为轴承内径；υ为材料泊松比。

轴承运行时，内外沟道曲率中心与球中心运转平衡位置之间的距离为

Δij=(fi-0.5)Dw+δij，

(2)

Δej=(fe-0.5)Dw+δej，

(3)

式中:fi、fe为内、外滚道沟曲率半径系数；Dw为滚珠直径；δij、δej为第j个滚珠与内外滚道间的接触变形。

变形后，轴承内、外沟道曲率中心间距离在轴向和径向分量分别表示为

Aaj=(fi+fe-1)Dwsinα0+δa+Riθsinψj，

(4)

Arj=(fi+fe-1)Dwcosα0+δrcosψj+uc，

(5)

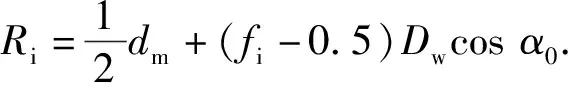
运行时，第j个滚珠与内、外滚道接触角可通过(6)式得到

(6)

根据勾股定理，得到变形协调方程组如下：

(Aaj-Xaj)2+(Arj-Xrj)2-[(fi-0.5)Dw+δij]2=0，

(7)

(8)

1.2 受力分析

高速角接触球轴承中，球的离心力引起接触变形和接触角变化，加之球自转轴线不断变化引起陀螺力矩和相应摩擦阻力，计算复杂。考虑通过轴承轴线和方位角ψj处球中心的平面，作用于球的载荷和力矩如图3所示。图3中：Mgj为第j个滚珠所受陀螺力矩，Fcj为第j个滚珠的离心力，Qij、Qej分别为滚珠与滚道之间的法向接触力；λij、λej为求解系数。

图3 滚珠受力平衡

滚珠与滚道之间的法向接触力表示为

(9)

式中：Kij、Kej为第j个滚珠与内外滚道间的负荷变形系数。

根据图3所示第j个滚珠的受力平衡情况，可以列出滚珠的平衡方程组为

(10)

Qijcosαij-Qejcosαej-

(11)

根据滚珠与轴承内圈的力学关系，列出轴承内圈的平衡方程为

(12)

(13)

式中:Fa为轴承所受轴向负荷；Fr为轴承所受径向负荷。

2 模型求解

根据第1节模型，采用Newton-Raphson迭代法对模型求解对该动刚度模型进行求解，按照图4算法设计开发了计算程序，求解精度ε=10-5.需要说明的是，内圈倾斜角θ并不是作为一个未知量经迭代求解得出，而是通过预先给定它的值来研究内圈倾斜角对轴承动态特性的影响规律。采取这种处理方式有两个原因：1)内圈倾斜角通过实验测试的方法易于获得；2)内圈倾斜角对轴承动态特性的影响很大，如果将其作为迭代求解的未知量，则很难得出收敛的结果。

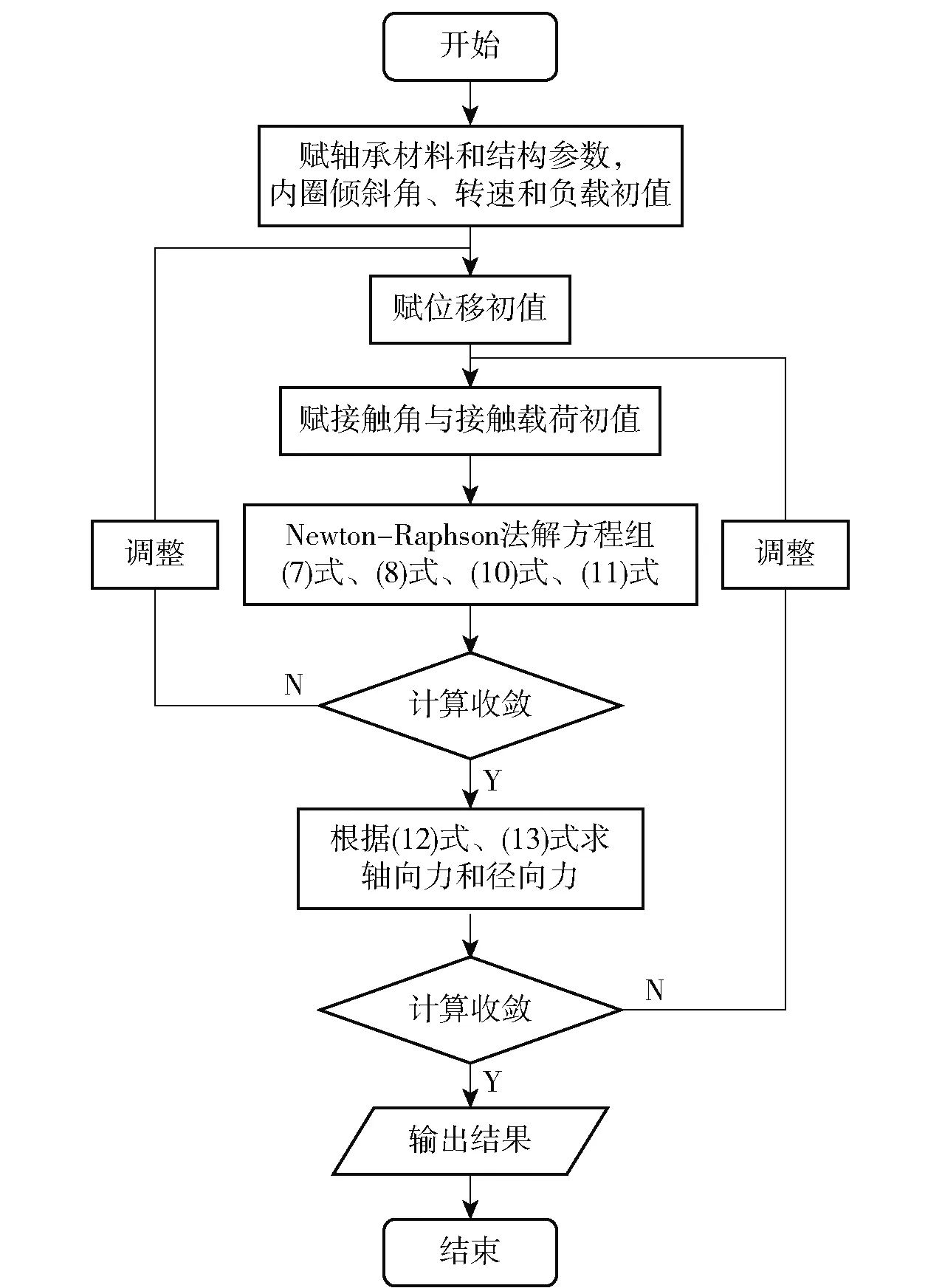
图4 角接触球轴承算法设计

3 计算结果与分析

使用自编程序与ROMAX软件对7206轴承(基本结构参数见表1)计算实例进行对比，对比结果如图5所示。由于ROMAX软件输出中不包含诸如轴承的旋滚比、滚珠公转转速和动刚度等参数结果，仅对轴承接触角和内、外圈最大接触应力进行对比。从表1中的对比数据来看，本文计算结果与ROMAX软件的计算结果十分吻合，最大计算差距3.7%.由此表明，本文分析模型所编制的程序可用于后续的分析。

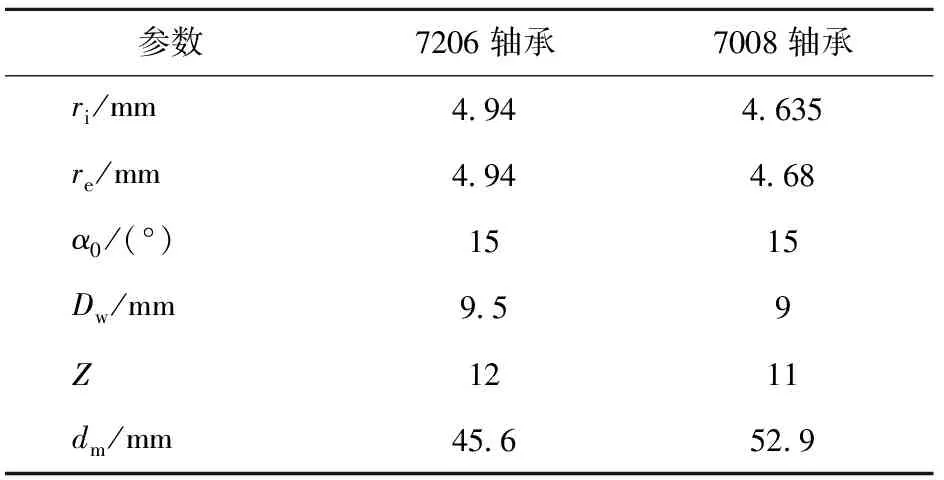
表1 轴承结构参数

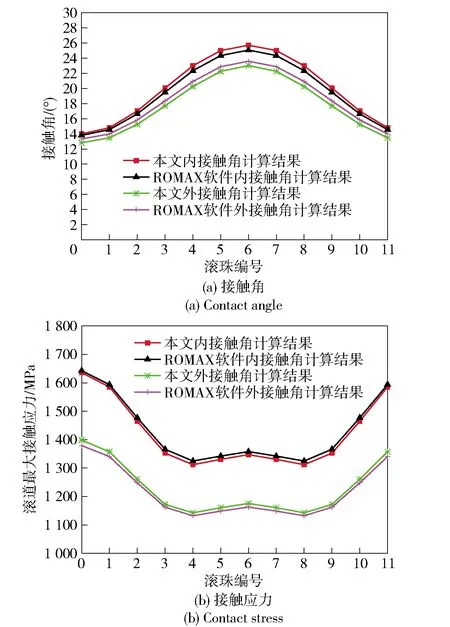
图5 计算结果对比

以7008轴承(基本结构参数见表1)为例开展研究。通过对接触角、接触应力、旋滚比、滚珠公转速度、刚度5个项点进行计算分析表征轴承动态特性变化。

3.1 内圈倾斜角对不同转速工况下轴承动态特性的影响

观察图6(a)、图6(b)可知，内圈倾斜角引起轴承内、外圈接触角波动变化，不同转速下波动规律基本一致，表明内、外圈接触角波动主要受内圈倾斜角影响，转速对其影响不大。

观察图6(c)、图6(d)可知，随转速升高，内圈倾斜角所引起的轴承接触应力波动变弱。同样是6′倾斜角，当转速为10 000 r/min时，内、外圈最大接触应力峰值较无内圈倾斜角时分别变化8.0%、8.4%；当转速为30 000 r/min，内、外圈最大接触应力峰值较无内圈倾斜角时分别变化5.7%、3.8%.

观察图6(e)可知，轴承转速升高，内圈倾斜角引起旋滚比大幅增加。转速为10 000 r/min时，有6′倾斜角旋滚比最大值较内圈倾斜前增加了7.8%；转速为30 000 r/min时，有6′倾斜角旋滚比最大值较内圈倾斜前增加了14.0%.旋滚比增大意味着轴承磨损发热严重。

观察图6(f)滚珠公转转速随位置角的变化可知，轴承转速愈高，内圈倾斜角引起滚珠公转转速波动幅度愈大。转速为10 000 r/min时，6′内圈倾斜角引起滚珠公转转速波动最大变化量为80 r/min，占比0.8%；转速为30 000 r/min时，6′内圈倾斜角引起滚珠公转转速波动最大变化量为570 r/min，占比1.9%.这意味着转速为30 000 r/min时滚珠在公转周期内会经历更加剧烈的加速和减速过程。

由以上分析可知，轴承转速升高，内圈倾斜角所引起的轴承接触应力波动变弱，但旋滚比、公转转速波动变化均增强。这表明在高速下，内圈倾斜角更易引发与轴承热相关的失效模式，而非常见的疲劳失效。

图6(g)为轴承动态刚度随转速的变化曲线，由图6(g)可知：无论是否存在内圈倾斜角，随转速升高，径向刚度Kr、轴向刚度Ka和角刚度Kθ均呈下降趋势，且角刚度下降最快。

图6 内圈倾斜角对不同转速轴承动态特性的影响(Fa=1 kN，Fr=0 kN)

3.2 内圈倾斜角对单轴向载荷工况下轴承动态特性的影响

图7给出了内圈倾斜角为6′时不同轴向载荷轴承动态特性变化曲线。通过观察可以发现，轴向载荷增加显著增大内、外接触角和最大接触应力，但几乎不改变波动规律，且随着轴向载荷增大，增幅放缓。轴向载荷对内圈旋滚比和滚珠公转转速影响不大。无论是否存在内圈倾斜角，随轴向载荷增加，轴承动态刚度变化规律一致[17]。

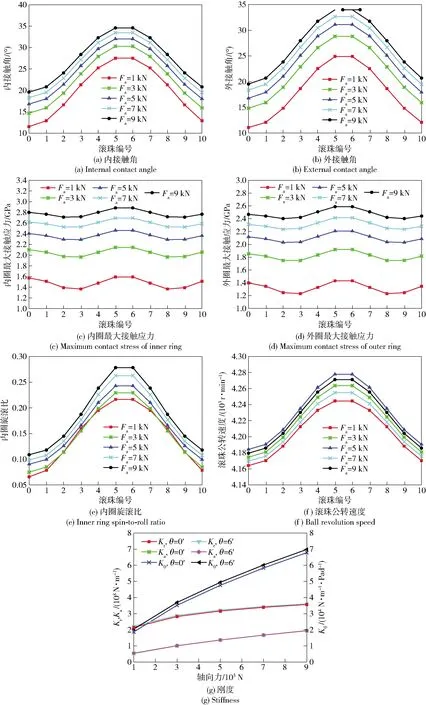
图7 内圈倾斜角对单轴向力工况下轴承动态特性的影响(Fr=0 kN, 轴承转速10 kr/min)

3.3 内圈倾斜角对联合载荷工况下轴承动态特性的影响

图8给出了内圈倾斜角对联合载荷工况轴承动态特性的影响。通过观察可以发现径向载荷的作用会引起轴承动态特性波动，存在一个适当的内圈倾斜角将径向载荷所带来的接触角、旋滚比、公转速度的波动降至最低。图8(g)为内圈倾斜角对联合载荷工况下轴承动态刚度的影响曲线，可以看到，内圈倾斜角的存在增大了轴承径向刚度和角刚度。以上这些变化对轴承稳定运转是有利的。然而，从图8(c)、图8(d)可知，内圈倾斜角会引起轴承套圈最大应力幅值增大，这削弱了轴承径向承载能力。尽管如此，在对轴承径向承载能力要求低的应用场合，通过适当初始内圈倾斜角使轴承非均匀预紧[18]，可降低轴承磨损和发热，增大轴承动态刚度，提高主机运转稳定性。

图8 内圈倾斜角对联合载荷工况下轴承动态特性的影响(轴承转速10 kr/min)

3.4 内圈倾斜角对不同材料滚动体轴承动态特性的影响

内圈倾斜角对不同材料滚动体轴承动态特性的影响如图9所示。由图9可知，受内圈倾斜角影响，氮化硅陶瓷球轴承内、外圈接触角波动较钢球轴承小，氮化硅陶瓷球轴承旋滚比和滚珠公转转速也远小于钢球轴承。图9(g)、图9(i)为不同滚珠材料轴承动态刚度变化曲线，从中可以看到，氮化硅陶瓷球轴承的动态刚度大于钢球轴承，随转速提高，氮化硅陶瓷球轴承动态刚度下降速度小于钢球轴承。此外，无论是钢球轴承还是氮化硅陶瓷球轴承，轴承径向刚度和角刚度因内圈倾斜角作用而显著增加，轴向刚度受内圈倾斜角影响较小，几乎没有改变。相同的工况下，陶瓷球轴承比钢球轴承有着相当多的优势，具有更低的磨损和发热、更高的刚度及运转稳定性。

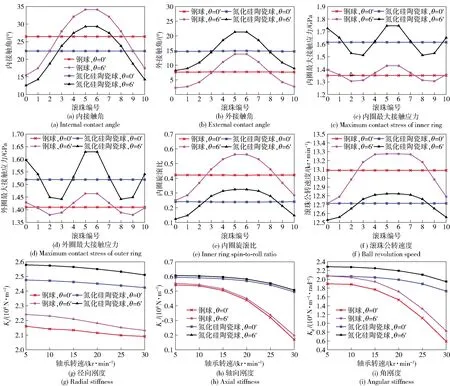
图9 内圈倾斜角对不同材料滚动体轴承动态特性的影响(Fa=1 kN, Fr=0 kN，轴承转速30 kr/min)

尽管如此，从图9(c)、图9(d)可见，氮化硅陶瓷球轴承接触应力对内圈倾斜角更加敏感，受内圈倾斜角影响接触应力波动更强烈，径向承载能力下降更多。可以看到，有6′倾斜角时：氮化硅陶瓷球轴承内、外圈最大接触应力峰值较无内圈倾斜角时分别变化8.0%、7.2%；钢球轴承内、外圈最大接触应力峰值较无内圈倾斜角时分别变化5.6%、3.8%.鉴于此，使用氮化硅陶瓷球轴承时，应更加严格地控制轴承配合件的形位公差，减小安装后内圈倾斜，否则易造成轴承提前失效。

4 结论

本文给出一种综合考虑内圈倾斜角、高速离心效应的轴承分析计算模型，采用Newton-Raphson法求解该模型，研究了内圈倾斜角对高速角接触球轴承接触角、接触应力、旋滚比、滚珠公转转速以及刚度的影响。得出如下主要结论：

1)轴承转速升高，内圈倾斜角所引起的轴承接触应力波动变弱，但旋滚比、公转转速波动变化均增强。这表明在高速下，内圈倾斜角更易引发与轴承热相关的失效模式，而非常见的疲劳失效。

2)对于承受联合载荷的角接触球轴承，适当的初始内圈倾斜角可大幅降低由径向载荷所带来的接触角、旋滚比、公转速度的波动，显著增大轴承径向刚度和角刚度，但同时也会减弱轴承径向承载能力。因此，在某些对轴承径向承载能力要求低的应用场合，通过适当初始内圈倾斜角使轴承非均匀预紧，可在一定程度上降低轴承磨损和发热，增大轴承动态刚度，提高主机运转稳定性。对于本文所研究的轴承及对应的工况，-4′的内圈倾斜角可最大程度减弱由径向载荷带来的轴承动态特性不均匀分布。

3)内圈存在倾斜角时，氮化硅陶瓷球轴承在接触角、内圈旋滚比、公转转速、动态刚度方面表现均优于钢球轴承，但与钢球轴承相比接触应力受内圈倾斜角影响波动更加剧烈，径向承载下降较多。因此，使用氮化硅陶瓷球轴承时，应更加严格地控制轴承配合件的形位公差，减小安装后内圈倾斜，否则易造成轴承提前失效。