截卵形弹体Taylor撞击的变形特点和冲击载荷特性

李俊承，陈刚，黄风雷，卢永刚，谭晓军，黄魏银

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081；2.中国工程物理研究院 总体工程研究所，四川 绵阳 621999)

0 引言

Taylor撞击实验是由Taylor[1]和Whiffin[2]等建立的一种测量高应变率条件下材料动态屈服应力的实验方法，实验采用平头圆柱形弹垂直撞击刚性靶面，通过对回收弹体外形尺寸的测量来获得材料的动态屈服应力。该方法操作简单、分析方便，广泛用于研究金属材料[3-6]在高应变率下的动态力学行为，此外还被用于高聚物材料、泡沫金属、玻璃等材料的研究中[7-9]。由于在Taylor撞击实验中可以容易地实现大变形、高应变率(104～107s-1)以及高温升，因此Taylor撞击实验也经常被用于本构模型的校验，通过与数值模拟相结合，Taylor实验发展为获取材料本构参量、模型校验和检验程序算法的手段[10-13]。经典的Taylor理论提出以来，研究者还不断在各个方面对其加以改进，如对运动方程的改进、对实验结果分析的改进、对实验测试手段和测试技巧的提高等[14-16]。同时在实验方法上也得到扩展，例如：将刚性靶扩展到变形靶体，研究破片的终点弹道效应[17]；将刚性靶替代为与弹体相同材料、相同直径的撞击杆，开展对称Taylor碰撞研究[18]；通过测试撞击靶背面的冲击力，研究聚合物复合材料的抗冲击、吸能特性等[19]。

目前有关Taylor撞击实验的研究中，大多数还是集中在材料本构参数获取、损伤模型验证等方面，而对于撞击产生的载荷以及载荷的应用关注较少。经典的Taylor撞击实验采用平头弹作为实验件，其弹体撞击产生的变形模式和载荷特征较为固定，无法将其应用在特定脉冲形状的冲击加载中。Taylor撞击实验本身具有冲击能量大、实验成本低、重复性好等优点，当适当放宽外形约束、改变弹体头部形状时，该实验方法具备产生不同脉冲形状冲击载荷的潜力，在冲击载荷模拟、高g值实验加载方面具有一定的应用前景；同时，不同头部外形的撞击过程能够产生更加丰富的变形模式和应力状态，可为材料模型及参数验证提供更多的选择。因此，开展不同头型弹体Taylor撞击的理论及实验研究，具有实际的研究意义和工程应用价值。

本文以典型的截卵形弹体为研究对象，基于Taylor撞击理论建立截卵形弹体的Taylor撞击分析模型，并对经典理论中的动量冲量守恒方程进行修正，使模型的预测结果更接近实际。设计并开展了具有相同外径、相同质量的截卵形弹、平头弹Taylor-Hopkinson撞击实验，实验记录了试件的撞击变形过程，并获得了由Hopkinson杆应变描述的撞击载荷历程。重点对比分析了两种头型弹体在变形模式、冲击载荷特征等方面的差异，讨论了弹体在撞击过程中经历的整体高g值过载，并基于建立的理论分析模型分析了产生不同脉冲形状冲击载荷的原因。本文研究可为弹体撞击动态响应分析、冲击载荷模拟控制、高g值加载实验件设计等提供参考。

1 理论分析

1.1 截卵形弹的Taylor撞击分析模型

基于经典的平头弹Taylor撞击理论，将撞击产生的应力波在弹体中来回传播、弹体速度逐渐降低的不连续的分阶段运动过程近似看成一个连续运动过程[20]。截卵形弹Taylor撞击的分析示意如图1所示，图1中：h为弹塑性界面和刚性靶面的距离，即塑性区长度；x为尚未压缩成塑性的弹性区长度；u为弹塑性界面向左传播的速度；v为无应力区向前的运动速度；Rh为弹体顶部半径；Rc为圆柱段半径；r=f(x)为头弧部的半径变化函数；L0为弹体初始长度；v0为初始撞击速度。另设弹体材料密度为ρ，弹性波波速为ce，弹体材料动态屈服强度为σd.

图1 截卵形弹Taylor撞击连续模型

根据运动关系可得

(1)

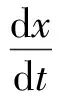
(2)

假设材料是不可压缩的，在dt时间内有一段截面为S0、长度为(u+v)dt的弹性区材料压入了塑性区域，变成了截面为S1、长度为udt的塑性区材料，但体积不变，于是得连续方程：

S0(u+v)=S1u.

(3)

考虑在dt时间内的动量冲量守恒，在时间内有ρS0(u+v)dt的材料以速度v进入塑性区域，这些动量转化为塑性区域中压缩应力σd的合力增加部分在dt中的冲量，根据动量守恒方程可得

ρS0v(u+v)=(S1-S0)σd.

(4)

对于平头弹，由应力波在弹性区内传播和尾部自由端反射后引起弹性区的速度减小量Δv为

(5)

(1)式～(5)式组成了平头弹Taylor撞击理论的方程组，5个方程含5个待定量，采用数值积分方法对方程组进行求解，起始条件为：当t=0时，v=v0,x=L0,h=0,S=S1；终止条件：当t=t2时，v=0,x=L2,h=h2,S=S0,u=0.

对于截卵型弹，头部撞击区域由平头弹的等圆截面体变为了连续变圆截面体。根据应力波传播原理，撞击产生的弹性波σi在传播过程中遇到截面发生变化(假设由截面S2向截面S3传播)将产生反射波σr和透射波σt，根据截面S2、S3两侧的总作用力和质点速度相等条件，可求得

式中：vt为跨过半径为r处截面的质点速度；vi为跨越前的质点速度。

令某时刻应力波在半径为r处截面向半径为r+Δr处截面传播，其中Δr足够小，则根据透射波和入射波关系可以写为

略去式中的高阶项Δr2并简化方程，得

(6)

同理，vt与vi的关系为

(7)

从(6)式和(7)式可知，弹性波在连续变圆截面体传播过程中，应力幅值、质点速度均随着截面处半径的增大而减小。当应力波到达弹体圆柱段后将向弹尾自由传播，此时应力波幅值不再发生变化。

因此，对于截卵形弹，在头部撞击产生的弹性压缩波到达弹体圆柱段之前(f(x)≤Rc)，由于传播过程中截面发生变化，不同截面处质点速度将有所变化。因此，弹性波往返传播一次，质点速度的变化量应该包括两部分：变截面弹性区传播引起的速度变化Δv1和尾部自由端反射作用引起的变化Δv2.根据(7)式，δt时间内由变截面传播引起的质点速度变化为

(8)

当应力波到达弹体圆柱段后，应力波幅值已由撞击面的σd减小为σt|f(x)=Rc，参照(5)式和(6)式，由尾部自由端反射作用引起的质点速度变化为

(9)

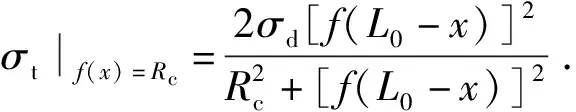
因此，对于截锥形弹体，当塑性变形区域还未到达弹体圆柱段时，弹性波在弹性区往返传播一次，弹体质点速度的变化为

(10)

当塑性变形区域到达弹体圆柱段后，弹性波往返传播一次，弹性区质点速度变化量的表达式与平头弹的相同。结合(1)式～(4)式，根据与平头弹相同的起始条件和终止条件，采用数值积分方法便能对截卵形弹体的Taylor撞击过程进行预测。对于图1中所示的截卵形弹体，假设头部曲径比为ψ，则头弧部半径变化函数为

(11)

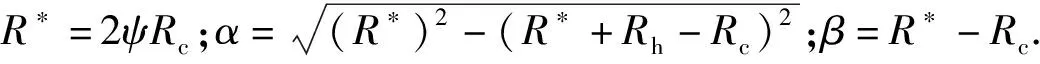
1.2 Taylor理论动量冲量修正

Taylor理论假设塑性区面积瞬时从S0变为S1，因此建立了(4)式所示的动量冲量守恒方程。事实上，塑性区面积的扩展是一个随时间变化的过程，虽然对于扩展的具体过程并不确定，但在撞击初始时刻即t=0 μs时，弹体刚接触到刚性撞击面，此时接触面的扩展速度应该是0 m/s；当撞击过程结束即t=Δt时，接触面停止扩展，此时接触面的扩展速度也应该是0 m/s.即如果将接触面的扩展分为两个阶段，在[0,Δt]的前半段，接触面扩展速度是逐渐增大的，而在[0,Δt]的后半段，接触面扩展速度是逐渐减小的。基于此，假设在任意时刻t，接触面S的扩展速度符合半正弦函数变化，为

(12)

式中：a为待定系数。对(12)式进行积分，得

式中：C为常数。根据撞击的起始条件(t=0,S=S0)和终止条件(t=Δt,S=S1)可求得

从而Δt时间内任意时刻t的接触面积为

因此，在Δt时间内压缩应力σd的合力增加部分冲量I应该为

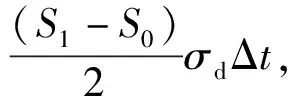
于是，动量冲量表达(4)式可修正为

(13)

对比(4)式和(13)式可知，修正后的冲量是原来的1/2.采用上述理论分析模型对文中第2节的实验进行预测，图2给出了两种头型弹体无量纲剩余长度与撞击速度曲线的理论预测结果和实际实验测试结果对比，图中纵坐标为无量纲剩余长度(剩余长度Lf与初始长度L0之比)。从图2中可以看出，理论分析模型与实验结果具有较好的一致性，修正后的理论值较Taylor理论值有所降低，其值更接近于实验值，修正后的理论预测值最大误差约为3%，表明理论分析模型能够较好地预测实验结果；不同头型弹体撞击后的剩余长度均随着撞击速度的增加而减小；相同撞击速度下，平头弹的弹体剩余长度较截卵形弹大，反映出平头弹具有更强的抗变形能力。

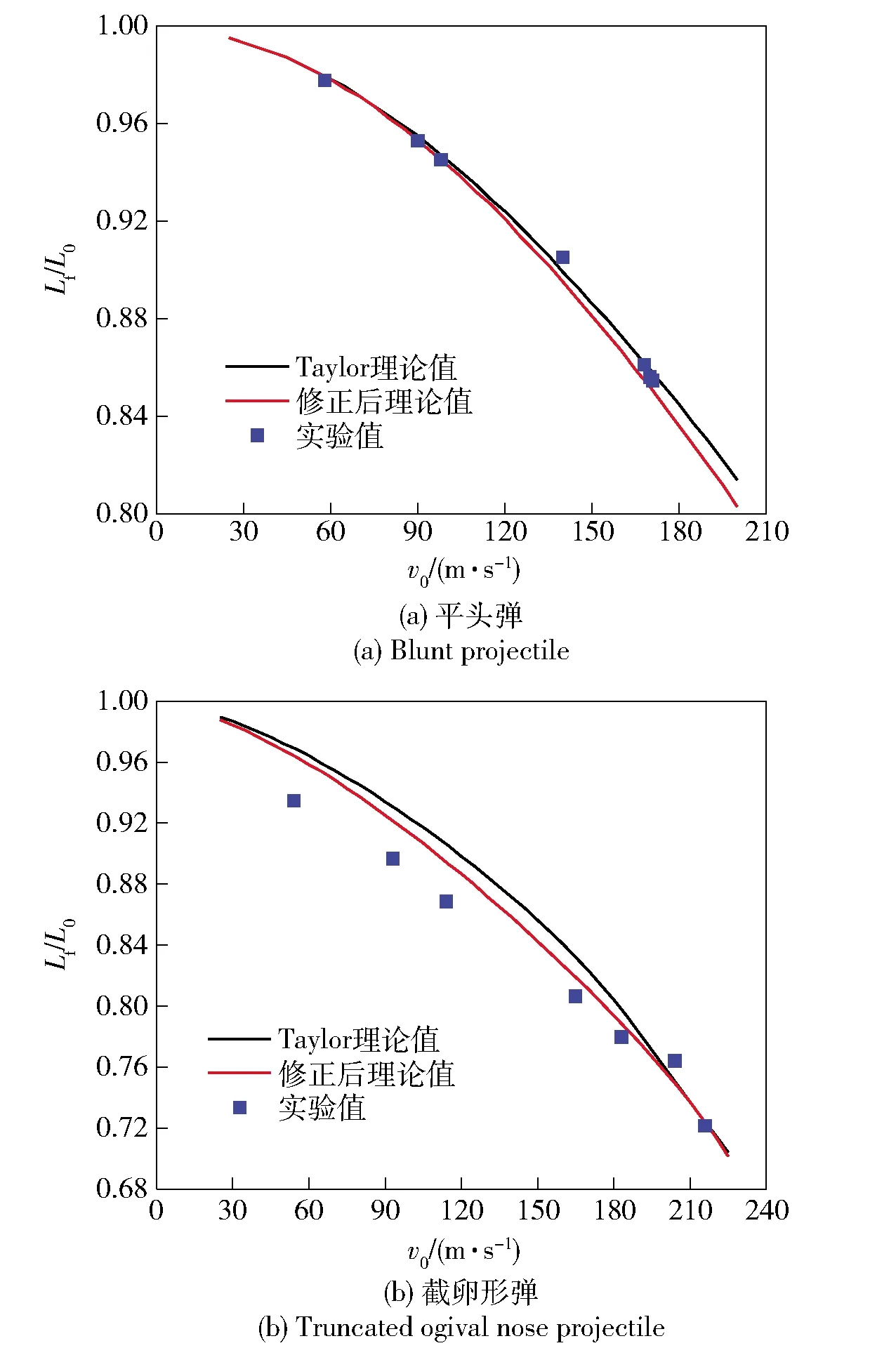
图2 理论预测与实验数据对比

2 Taylor-Hopkinson撞击实验

2.1 实验弹尺寸及材料

开展冲击实验，对截卵形弹的撞击变形特点和冲击载荷特性进行详细分析。实验所设计的截卵形弹体如图3所示，弹体头部曲径比为3、顶部直径为5 mm、圆柱段直径为25 mm，质量为133.9 g；作为对比，设计具有相同直径和质量的柱形平头弹，平头弹长度为100 mm；实际加工完成的实验弹如图4所示。

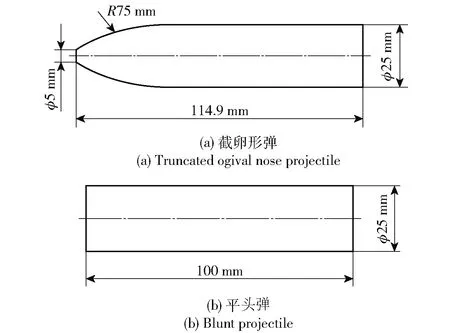
图3 弹体结构示意图

图4 实验弹实物图

弹体材料采用3A21铝合金，3A21为铝锰系不可热处理强化的铝合金，在退火状态下具有较高的塑性且具有对应变率不敏感的特性，材料的应力-应变曲线如图5所示。

图5 3A21铝合金应力-应变曲线

2.2 实验布置

Li等[21]、Liu等[22]在研究泡沫金属的动态力学性能中，将Taylor撞击实验的刚性撞击靶体替换为Hopkinson入射杆，杆的强度远高于试件材料，确保入射杆在冲击过程中不发生塑性变形，使用测量仪器记录入射杆中的应变信号，通过入射杆的应变输出信号，测量了受撞击一端的压力。

参考上述实验方法，整个实验系统由空气炮、弹体、激光测速仪、数字高速摄影机、Hopkinson入射杆、应变测试系统等组成，布置示意如图6所示，实际布置见图7.Hopkinson入射杆长3 m、直径为50 mm、材料为7A04高强度铝合金，材料屈服应力达到550 MPa，远高于3A21铝合金的塑性流动应力。在入射杆中部粘贴应变片测试撞击载荷，应变测试系统采样频率为10 MHz；在发射管出口处放置激光测速仪测量弹体初速；用数字高速摄影机记录弹体在撞击过程中的变形历程，采集帧率为50 000帧/s.为防止入射杆在多次高速撞击下可能发生的塑性变形，保证每次撞击相同状态的撞击面，在入射杆的撞击端粘贴与入射杆相同材料、相同直径的垫块，每发实验后更换一个垫块。

图6 实验布局示意图

图7 实验布局照片

3 实验结果与分析

实验共计开展14发，两种头型弹体各开展7发，撞击速度在50～220 m/s之间。各发实验的具体信息和结果汇总见表1.表1中：m为弹体质量；Di为弹体头部初始直径；Dc为弹体圆柱段直径；Df为实验后回收到的弹体顶部直径。

表1 实验信息及结果

3.1 弹体撞击变形及对比分析

图8为平头弹在171 m/s撞击速度下的高速摄影照片。从图8中可以看出：平头弹撞击入射杆后(t=0 μs)，弹体头部与靶面紧密接触，撞击端面近似保持平面；随着撞击时间的增加，弹体逐渐发生压缩变形，由于受到速度方向靶面的阻碍作用，材料沿弹体径向流动，头部截面积扩张，撞击端头部形成蘑菇状镦粗，弹体前端呈膨胀的喇叭口型；t=160 μs后，弹体尾部轮廓不再发生前移，此时镦粗变形停止，头部塑性区停止扩展；t=180 μs后，弹体尾部轮廓线出现了较为明显的反弹后移，此时撞击过程已结束。图9为截卵形弹在165 m/s撞击速度下的高速摄影照片，与平头弹类似，弹体撞击入射杆后(t=0 μs)，端面与入射杆紧密接触，弹体逐渐发生压缩变形，材料沿弹体径向流动，头部截面积扩大；撞击开始200 μs后，弹体尾部轮廓不再发生前移；240 μs后，弹体出现反弹后移，撞击过程结束，撞击持续时间较平头弹有明显增加。

图8 平头弹Taylor撞击高速摄影图片

图9 截卵形弹Taylor撞击高速摄影图片

不同撞击速度下回收的平头弹外形对比如图10所示。由图10可见撞击端出现典型的蘑菇头镦粗，撞击速度越高，其头部镦粗越明显且在长度方向的压缩量也越大。不同撞击速度下截卵形弹体的外形对比见图11，从中可看出：当撞击速度小于165 m/s时，顶部镦粗后的直径小于弹体直径；当速度高于165 m/s时，撞击端呈现典型的蘑菇头镦粗，边缘有细微开裂。由于截卵形弹体具有尖拱形头型，变形更集中于弹体头部，局部变形量比平头弹大的多，从图11中还可以看到，在撞击端侧面有材料大变形形成的表面褶皱。

图10 不同撞击速度下平头弹试件照片

图11 不同撞击速度下截卵形弹试件照片

将回收弹体沿轴向选点测量，获得变形前、后弹体外形尺寸，并将其与原始弹体尺寸一同作图，得到撞击前、后弹体外形对比如图12所示。由图12可见：弹体尾部基本处于未变形状态，越靠近撞击端弹丸逐渐膨胀成蘑菇形；相同头型弹体按照撞击速度从低到高，依次发生头部镦粗变形，头部镦粗+边缘开裂变形；长度方向压缩量方面，截卵形弹要明显高于平头弹。

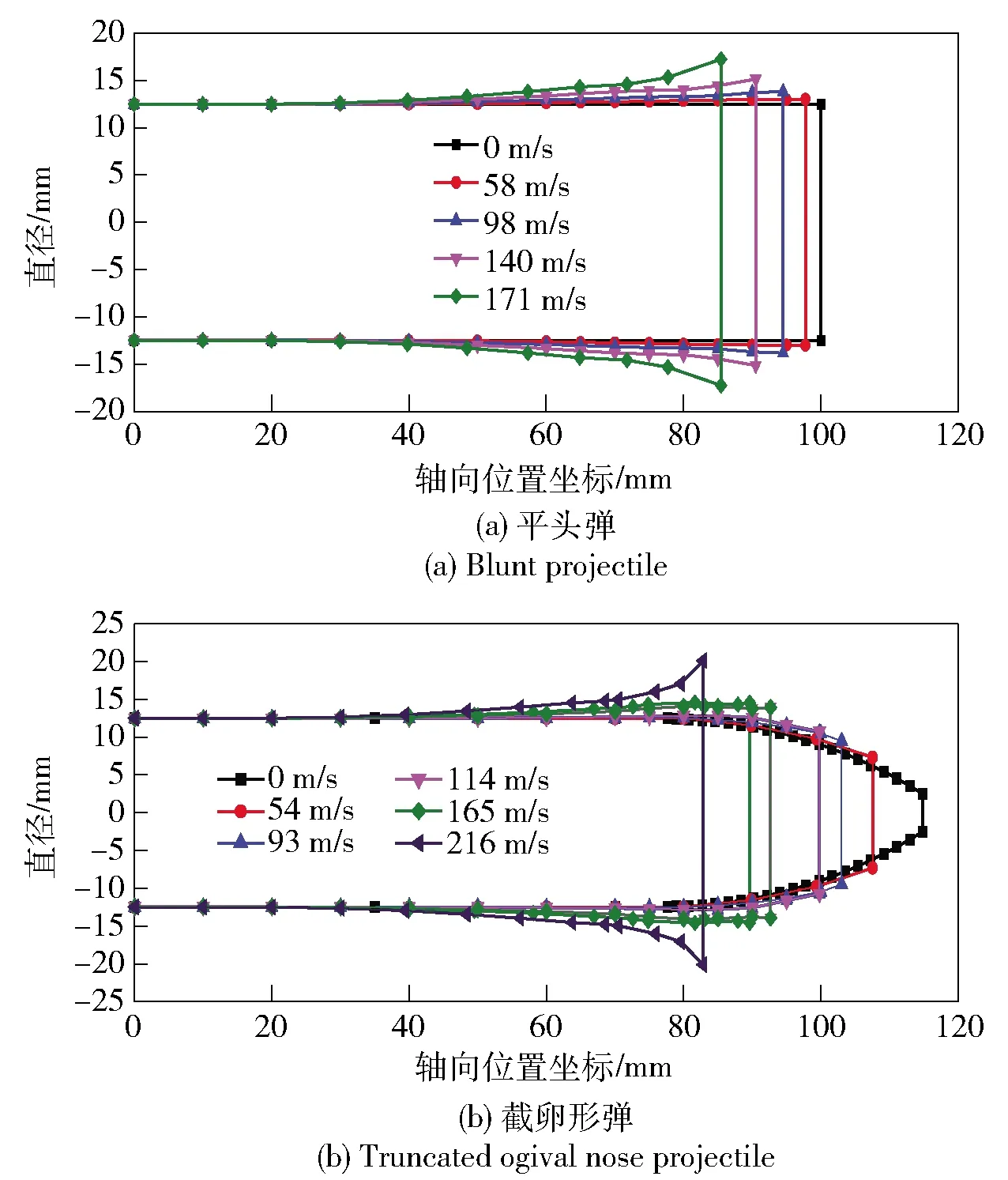
图12 不同撞击速度下弹体初始和最终变形比较

对所有撞击后的弹体长度改变量和顶部直径改变量进行统计对比，不同因素的影响关系见图13和图14.从图13和图14中可以看出：弹体剩余长度均随着撞击速度的增加而减小，顶部直径随着撞击速度的增加而增大；相同撞击速度下，平头弹弹体长度的变化量小于截卵形弹；在顶部直径改变量方面，截卵形弹体相对改变量要明显高于平头弹，反映出平头弹较截卵形弹具有更强的抗变形能力，而截卵形弹具有更显著的头部形状变化特征。

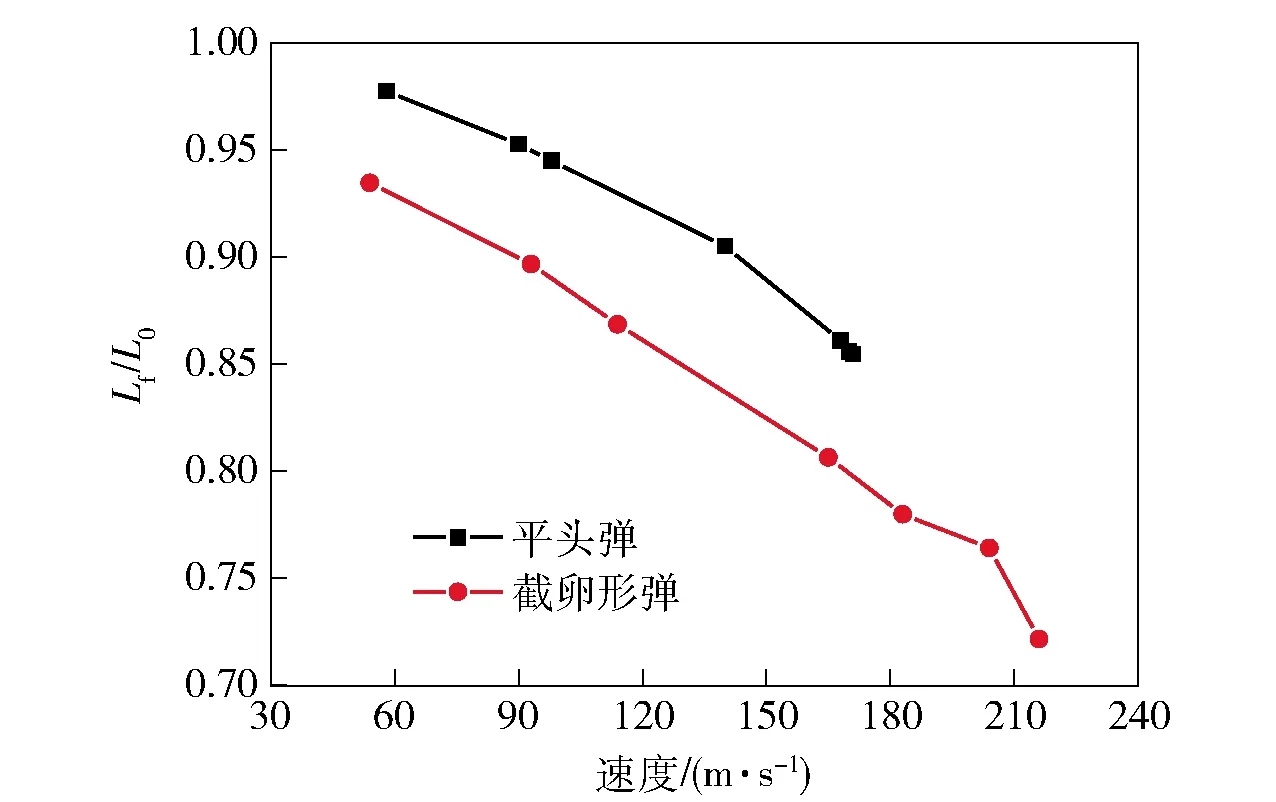
图13 弹体剩余长度-撞击速度曲线比较

图14 头部直径-撞击速度曲线比较

3.2 撞击载荷对比

实验中，Hopkinson杆上测到的平头弹典型应变-时间信号如图15所示，包含一个撞击产生的入射脉冲信号和在入射杆自由端反射后形成的反射脉冲信号，两个信号之间无叠加，入射脉冲信号能够完整地反映撞击过程的撞击力变化。利用(14)式将应变转换为撞击端的冲击力：

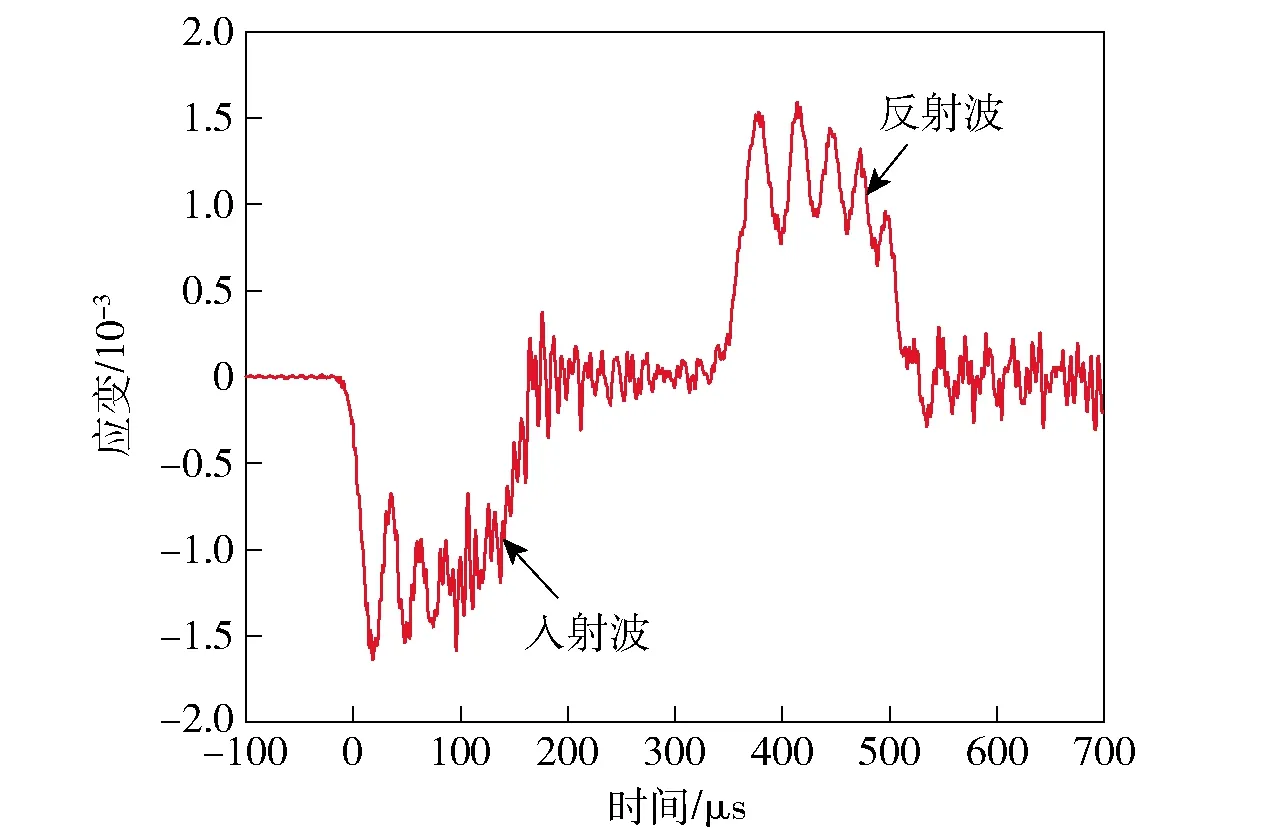
图15 平头弹典型应变-时间曲线(撞击速度171 m/s)

F(t)=Eb·ε(t)·Sb，

(14)

式中：Eb为入射杆弹性模量；ε(t)为实验中测得的杆中应变；Sb为入射杆的截面积。

采用(14)式对入射脉冲信号进行数据处理，得到弹体的加速度-时间曲线如图16所示。由图16可知，撞击过程中弹体整体经历了峰值约16.8×104g，持续时间约177 μs的冲击环境。将弹体加速度-时间曲线进行积分，得到弹体的速度变化曲线如图17所示，整个撞击过程弹体速度变化约为-174 m/s，与初始速度171 m/s相当。积分结果略高于初速，是由于撞击后弹体还有较小的反弹速度(约为-3 m/s)，与实验观测结果相符，表明应变测试信号能够正确地反映弹体的受力减速过程。

图16 平头弹体加速度-时间曲线(撞击速度171 m/s)

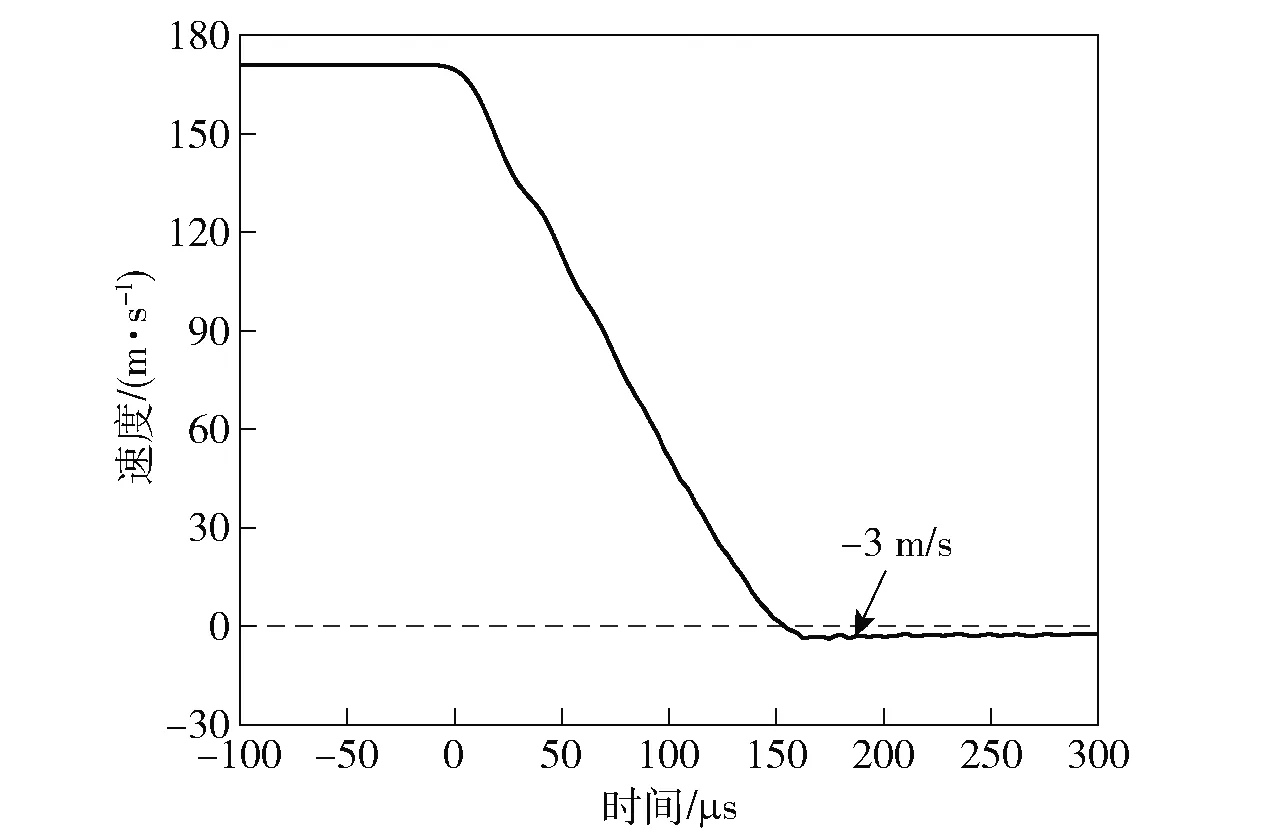
图17 平头弹体速度-时间曲线(撞击速度171 m/s)

采用相同的数据处理方法，对各发实验的应变测试数据进行处理，得到各发实验的撞击载荷峰值、载荷持续时间和弹体加速度峰值见表2.由表2可知，两种头型弹体在不同撞击速度下整体经历了峰值4×104g～18×104g，持续时间120～240 μs的冲击环境。

表2 撞击载荷信息统计

相同头型弹体在不同撞击速度下的撞击载荷曲线对比如图18和图19所示。由图18和图19可知对于同一种头型的弹体，不同速度下的载荷波形具有相似的变化特征：平头弹在不同速度下撞击载荷具有相同的上升速率，最大载荷达到时间基本一致，波形整体近似呈现为梯形；截卵形弹的载荷上升沿随撞击速度的提高而越发陡峭，最大载荷达到时间也随着速度的提高而提前，整体近似呈现为半正弦波脉冲。

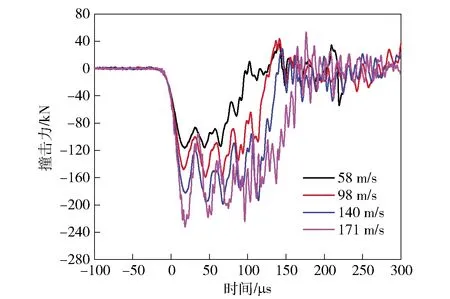
图18 不同撞击速度下平头弹撞击载荷曲线

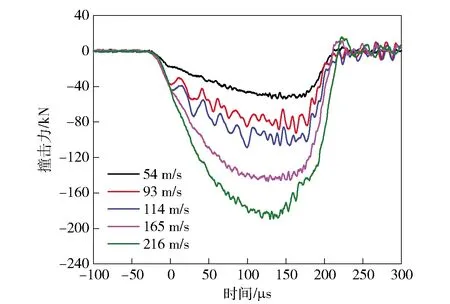
图19 不同撞击速度下截卵形弹撞击载荷曲线

两种头型弹体在相近撞击速度下的撞击载荷曲线对比如图20所示。由图20可见：整体变化趋势上，平头弹撞击载荷的上升沿更陡峭，在撞击初期迅速达到峰值，整个撞击过程持续时间较短，曲线整体振荡较大；截卵形弹在撞击初期，载荷曲线上升缓慢，最大载荷达到时间较平头弹滞后，撞击作用时间较平头弹长、脉冲宽度明显增加，但最大载荷值有一定程度降低，曲线整体振荡较小、波形平滑。

将所有撞击载荷曲线数据进行整理，得到最大载荷值和载荷持续时间随撞击速度的变化曲线，如图21和图22所示。对比曲线的变化趋势可知：在相同速度下，平头弹撞击产生的载荷峰值高，但脉冲宽度小；截卵形弹体撞击产生的载荷峰值小，但脉冲宽度明显增长；两种头型弹体撞击产生的载荷峰值均随撞击速度的提高而显著增加；对于脉冲宽度，不同头型弹体的表现略有差异，平头弹脉冲宽度随撞击速度提高而增大，而截卵形弹体在不同撞击速度下的脉冲宽度在小范围内波动。从图22中可以看出，截卵形弹体的变化曲线近似为一条直线，即速度的显著提高并没有带来脉冲宽度的明显变化，表明对于截卵形头部的弹体，载荷持续时间具有对速度不敏感的特点。

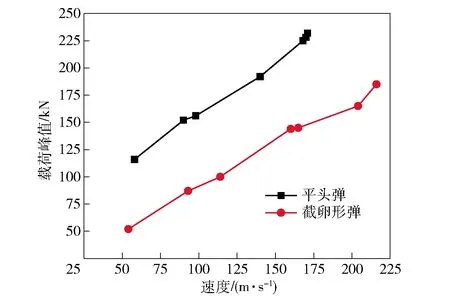
图21 撞击速度与载荷峰值曲线

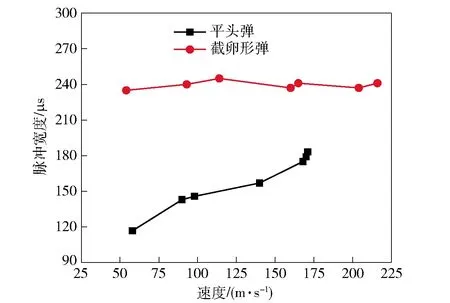
图22 撞击速度与脉冲宽度曲线

3.3 产生不同脉冲形状撞击载荷的原因分析

由实验结果分析可以知，弹体头型的改变显著改变了冲击载荷的幅值、脉宽和波形等特征，采用本文提出的撞击分析模型对不同脉冲形状载荷的产生原因进行进一步分析。

撞击过程中，以弹性区质点的速度和加速度来近似表征整个弹体的速度和加速度，不同头型弹体在相同撞击速度(以150 m/s为例)下的时间历程曲线对比如图23所示。速度变化方面:平头弹的速度下降快，整个过程经历的时间短；截卵形弹在撞击初始时刻的速度变化则相对平缓，损失量较少，由此延长了整个作用时间。对应到弹体加速度曲线上：平头弹在撞击初期，加速度迅速达到一个较高水平，曲线上呈现为一个陡峭的上升沿；截卵形弹的加速度变化则相对平缓，在相同时刻，其加速度明显小于平头弹，曲线形状上近似呈现出圆弧形上升沿，与弹体的头部外形形状相似。

根据Taylor撞击理论，弹体速度变化由头部撞击产生的弹性波在弹体内往返传播引起。当头部形状发生改变时，弹性波在弹体中的传播路径由平头弹的等截面传播变为截卵形的连续变截面传播。由应力波传播理论，当在连续变截面体传播过程时，应力幅值、质点速度均随着截面半径的增大而减小，由此引起速度下降变缓，反映到弹体加速度曲线上，在撞击初期形成缓慢的上升沿；截面的半径变化规律由弹体头部外形函数r=f(x)决定，因此在加速度曲线上可以看到一个与弹体头部外形相似的上升沿。最终弹体头部截面形状的变化规律反映在加速度曲线上，影响了整个波形，这也是不同头型弹体产生不同脉冲形状撞击载荷的主要原因。

4 讨论

Taylor撞击实验的一个重要特点就是试件的头部发生塑性大变形，而尾部仍保持弹性状态。将Taylor撞击试件分成塑性变形区和弹性变形区两部分，就弹性变形区而言，该部分承受的冲击载荷由前端的塑性变形区产生和传递，试件前端的塑性变形区可以理解为冲击载荷的发生器，而后端的弹性变形区可以考虑为被冲击加载的部件；由本文分析可知，试件头部形状是载荷波形的主要影响因素，撞击速度主要影响载荷峰值，即通过弹体头部形状设计和撞击速度控制可以实现冲击环境特性的调控。

本文给出的实验和分析结果针对的是φ25 mm的实验件，但相关结果对于其他尺寸同样适用。基于此，可将被加载部件(如引信、弹载记录装置等)安装放置于Taylor撞击试件的弹性段尾部，如图24所示，在研究试件变形与冲击载荷特性关系的基础上，设计合适的弹体头部形状并控制撞击加载速度，可以实现需要的高g值冲击环境。例如，初步的分析表明，通过头型优化，对于质量约5 kg、φ120 mm的弹体，可以实现峰值3×104g～5×104g、持续时间1 ms左右的整体高g值加载环境。

5 结论

本文采用理论分析与实验研究相结合的方法，以撞击载荷主要为关注点，对截卵形弹、平头弹的撞击变形特点和冲击载荷特性进行了分析，讨论了弹体在撞击过程中经历的整体高g值过载，分析了产生不同脉冲形状撞击载荷的原因。得到主要结论如下：

1)相比于平头弹，截卵形弹体撞击产生的载荷峰值略小，但脉冲宽度较长，且不同撞击速度下的脉宽波动幅度较小；波形上，截卵形弹的撞击载荷曲线近似呈现为半正弦形，曲线整体振荡较小、波形平滑；而平头弹曲线整体振荡较大，整体近似呈现为梯形。

2)弹体头部形状显著改变了冲击载荷的波形、脉宽等特征。撞击速度决定了撞击能量，主要影响冲击载荷峰值，而头部形状是载荷波形的主要控制因素。

3)由实验测得的载荷反推，在撞击过程中试件整体上经历了幅值4×104g～18×104g，持续时间120～240 μs的高g值加载历程。

4)在相同的撞击速度下，截卵形弹体头部局部变形比平头弹要大很多，而且变形模式更加丰富，可以为材料模型及参数验证提供更多选择。

5)研究结果支持了将Taylor撞击实验应用于高g值实验加载的设想。

致谢中国工程物理研究院总体工程研究所的张方举研究员、谢若泽研究员、徐伟芳研究员在实验实施过程中给予了宝贵协助和指导！