基于同步压缩变换的阶比分析法在城市轨道交通车辆轴承故障诊断中的应用*
王 冰 魏志恒 王文斌 戴源廷 赵俣钧
(中国铁道科学研究院集团有限公司城市轨道交通中心, 100081, 北京∥第一作者, 高级工程师)
城市轨道交通车辆滚动轴承变转速运行时的振动信号包含了比恒转速运行时更为丰富的特征信息[1]。阶比分析[2-4]近年来越来越多地被用到变转速机械故障的诊断中,其基本原理是将非稳态的时域信号通过等角度重采样转换为准稳态的角域信号。目前国内外的阶比分析技术分为3种:采用鉴相装置的硬件式阶比跟踪、COT(计算阶比追踪)和基于瞬时频率估计旋转机械阶比追踪[5]。其中,鉴相装置的硬件式阶比追踪在工程应用中操作不方便,而且成本较高。COT虽然比硬件式阶比追踪方便,不需要特定的装置,但同样摆脱不了需提供转速信号的局限性[6]。
针对这些局限性,部分研究将STFT(短时傅里叶变换)用到阶比追踪的瞬时频率估计中,但是STFT的时频分辨率不高,易受到噪声干扰,会影响瞬时频率的提取。Wigner Distribution(维格纳分布)由于有交叉项的存在,难以提取瞬时频率曲线[7-8]。文献[9]在WT(小波变换)的基础上提出了基于SST(同步压缩变换)的时频分析方法,更适用于非平稳信号的分析。
与其他方法相比,SST的分辨率高,因此在提取瞬时频率曲线时的精度更高。基于此,本文提出基于SST瞬时频率估计的变转速轴承振动阶比分析方法:首先利用SST对轴承的变转速振动信号进行分析,得到其时频分布;然后提取转频的瞬时频率脊线,得到瞬时转频曲线,并根据转频曲线求取鉴相时标,对振动信号进行等角度重采样,获得角域信号;接着对角域信号采用Hilbert(希尔伯特)算法进行包络解调,求其包络阶次谱;最后通过分析包络阶次谱来判断滚动轴承是否存在故障,并分析其故障类型。
1 SST算法原理
SST以WT为基础,利用同步压缩算子提高时频脊线在时频谱上的分辨率,实现了对瞬时频率的提取与重构。设ψ(b)为小波母函数,则信号x(t)的连续小波变换为:
(1)
式中:
x(t)——振动信号;
W(a,b)——x(t)的连续小波变换结果;
t——时间变量;
a——尺度因子;
b——平移因子;

通过分析可知,在小波域中(a,b)位置的瞬时频率信息为:
(2)
式中:
ωx(a,b)——瞬时频率;
j——虚数单位。
文献[10]发现,无论a取何值,W(a,b)在b上的振荡特性均指向初始频率Ω,因此:
∂W(a,b)/W(a,b)=jΩ
(3)
根据定义的同步压缩变换,小波逆变换为:
(4)
(5)
式中:
x(b)——小波逆变换结果;
Cψ——相差系数;
ψ(aξ)——小波母函数。
对ωx(a,b)沿尺度a方向整合,归划到频域中ω=ωx(a,b)的位置上,则同步压缩变换定义为:
(6)
A(b)={a,W(a,b)≠0}
(7)
式中:
Sst(ω,b)——信号b的同步压缩函数;
ω——角频率。
通过式(6)的结果与相差系数Cψ,将信号的幅值归化到时频域中所在位置,最终获得高分辨率的时频谱。
2 基于SST的阶比分析
2.1 阶比分析
阶比分析是一种针对变频信号的分析方法,首先将非稳态频率变化的时域信号通过等角度重采样转化为准稳态的角域信号,然后再利用传统方法对角域信号进行处理。对于旋转机械而言,阶次指的是振动信号中所有频率与其转频的比值,两者的关系如式(8)所示,阶次为1.0表示该频率与转速频率一致。
f=lR/60
(8)
式中:
f——振动信号的频率,Hz;
l——阶次;
R——旋转轴转速,rad/min。
阶比跟踪是阶比分析中的关键步骤。基于瞬时频率估计的阶比分析方法,通过提取振动信号中的转速信息来实现阶比跟踪,无需增加特定的硬件装置。在基于瞬时频率估计的阶比分析中,棘手问题是对转频的瞬时频率予以准确估计。针对此问题,本文提出基于SST瞬时频率估计的阶比分析法。
2.2 基于SST瞬时频率估计的阶比分析
SST法能够将包含在振动信号中的瞬时转频信息精确地提取出来。根据瞬时转频的变化,计算出鉴相时标序列,对采集的振动信号进行重采样,将非平稳的时域信号转换成平稳的角域信号,最终得到精准的阶次谱,实现对轴承的故障诊断。如图1为基于SST瞬时频率估计的阶比分析方法。
基于SST瞬时频率估计的阶比分析,具体步骤如下:
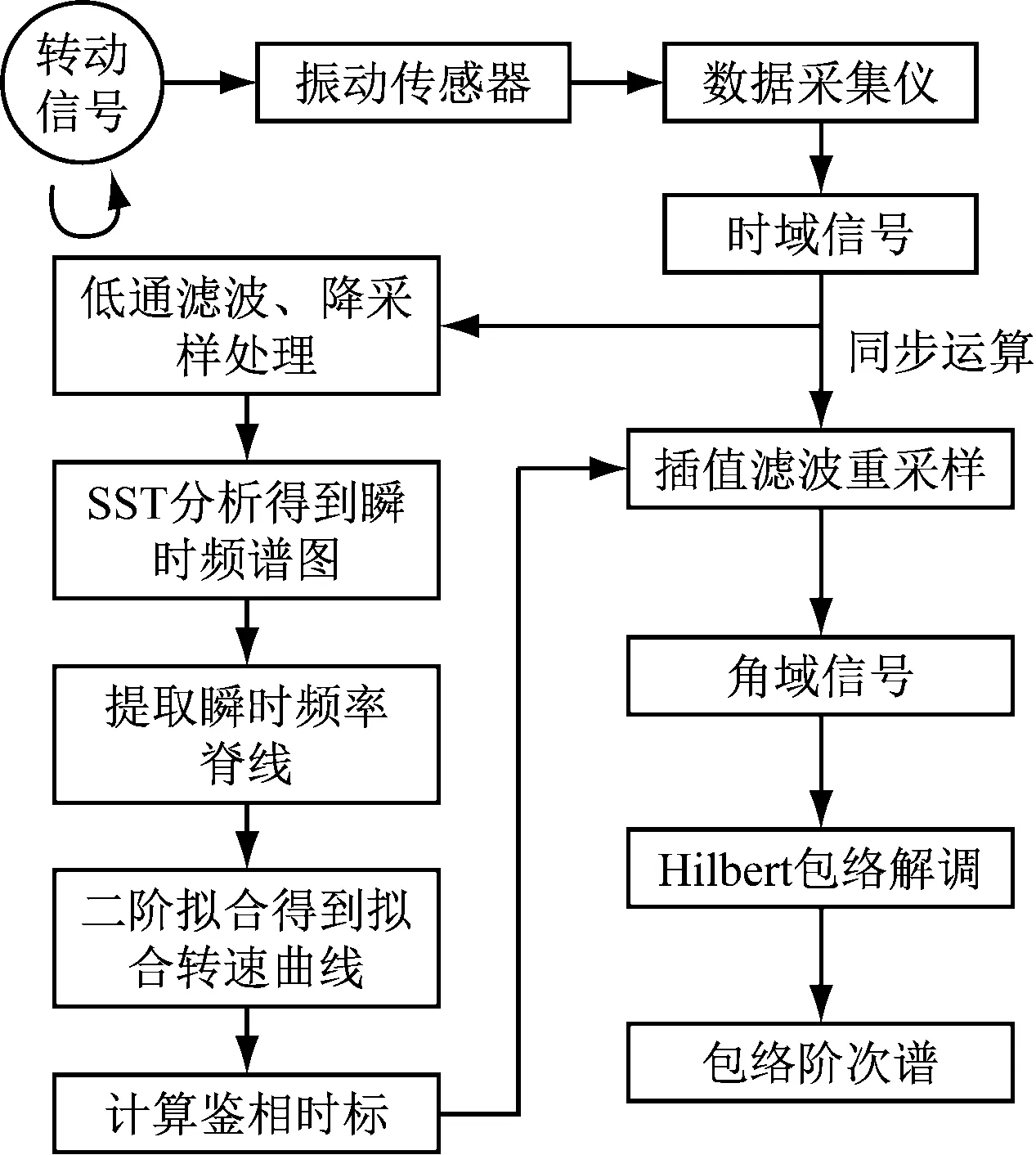
图1 基于SST瞬时频率估计的阶比分析流程图
步骤1:对采集的信号进行低通滤波和降采样处理,目的是去掉高频成分的干扰,更准确地提取瞬时频率。为了保证转速曲线在这个区间的完整性,低通滤波截止频率不能低于转频的最大值。
步骤2:在时频谱上利用峰值搜索的手段,得到转频的瞬时频率曲线fcs(k)(k为采样点序号),进而得到转速的瞬时频率。
步骤3:通过多项式对离散的fcs(k)进行拟合,获得瞬时频率拟合曲线fi(t)。在小范围内可以采用高阶项式拟合和样条拟合的方法来实现更精确的接近,这里取二阶多项式拟合,拟合方程为:
fi(t)=at2+bt+c
(9)
式中:
i——瞬时频率标志;
a、b、c——拟合系数。
步骤4:根据瞬时频率拟合曲线fi(t)计算鉴相时标序列Tn:

(10)
Δθ=π/Omax
(11)
式中:
n——采样时刻序列号;
N——采样序列长度;
T0——采集初始时刻;
Δθ——等角度采样的采样间隔;
Omax——最大理论阶次。
将式(10)积分,可得:
(12)
一般令T0=0,进一步计算获得重采样所需的Tn。
步骤5:利用鉴相时标序列,按照插值原理对原始数据进行等角度重采样,从而将非稳态的时域信号转换成准稳态的角域信号序列Y(Tn):
(13)
式中:
Y(Tn)——角域信号序列;
m——旋转角度;
Δts——时域采样间隔;
hs(t)——插值滤波器函数。
最后利用Hilbert算法对Y(Tn)进行包络解调,并通过FFT(快速傅里叶变换)获得包络阶次谱,实现对变频振动信号的阶比分析。
3 仿真试验分析
城市轨道交通列车出站后,一般以恒定加速度加速到某一设定车速,随后便保持恒速运行,该加速过程通常为线性变化。构造一个加速过程的信号:
m(T)=20Tsin(2π100T2)+10Tsin(2π250T2)+
9Tsin(2π350T2)
(14)
式中:
m(T)——构造的加速过程信号;
T——时间序列。
设置采样频率为2 000 Hz,采样点数为2 000,并添加SNR(信噪比)为-8的高斯白噪声。由式(14)可知,m(T)中有3个分量,假设:① 第1个分量为转速变化分量,则第1个分量的瞬时转频f0=200T;② 第2个分量的瞬时频率f1=2.5T;③ 第3个分量的瞬时频率f2=3.5f0。由阶次与转频的关系可得这3个分量的阶次分别为1.00、2.50、3.50。
图2为构造的仿真信号的波形及其频谱。从图2可以看出,频谱中频率出现渐变现象,很难找到故障特性信息。图3~4分别为理想瞬时频率与基于SST分析方法得到瞬时频率的结果,对比可以看出:随着幅值的增加,基于SST方法得到的时频曲线越来越清晰,并且集中性很强;且基于SST提取得到的瞬频脊线基本与理想的瞬频脊线相吻合。图5为拟合后的瞬时频率脊线与理想瞬时频率脊线的对比,发现两者几乎重合,说明采用SST法能够准确提取振动信号中的转频信息。

图2 仿真信号时域及频谱

a) 时频分布

a) 时频分布

图5 基于SST提取的频率脊线与理想信号比较
利用拟合的瞬时频率曲线进行插值滤波得到鉴相时标序列,根据鉴相时标序列对原始的振动信号进行等角度重采样。在等角度采样之前需要设置最大阶次为20。如图6 a)所示,等角度采样后的角域信号在转动周期中分布比较均匀。图6 b)的包络阶比谱中,阶次1.002与理想阶次1十分接近,因此可以认为是转频信息,而阶次2.516与3.518恰好对应仿真信号中第2、3个分量成分。

a) 角域信号
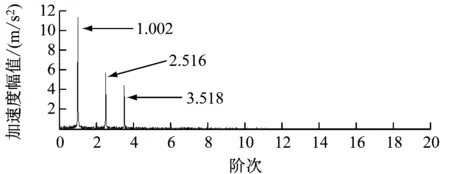
b) 包络谱
4 试验验证
对包含轴承升速过程的振动信号进行分析,并与经STFT后的分析结果进行对比。采用转子试验台作为试验平台,测点分布如图7所示,预埋故障轴承位置靠近电机端(测点3),轴承型号为ER-12K。该轴承的故障特征频率系数如表1所示,例如,内圈故障特征频率为4.950×转频,则经过阶比分析后的特征阶次即为4.950。将转子试验台的转速频率变化范围设置为0~24 Hz,采样频率为6 000 Hz。为了得到较好的升速过程,选取采集的信号长度为30 000采样点数。
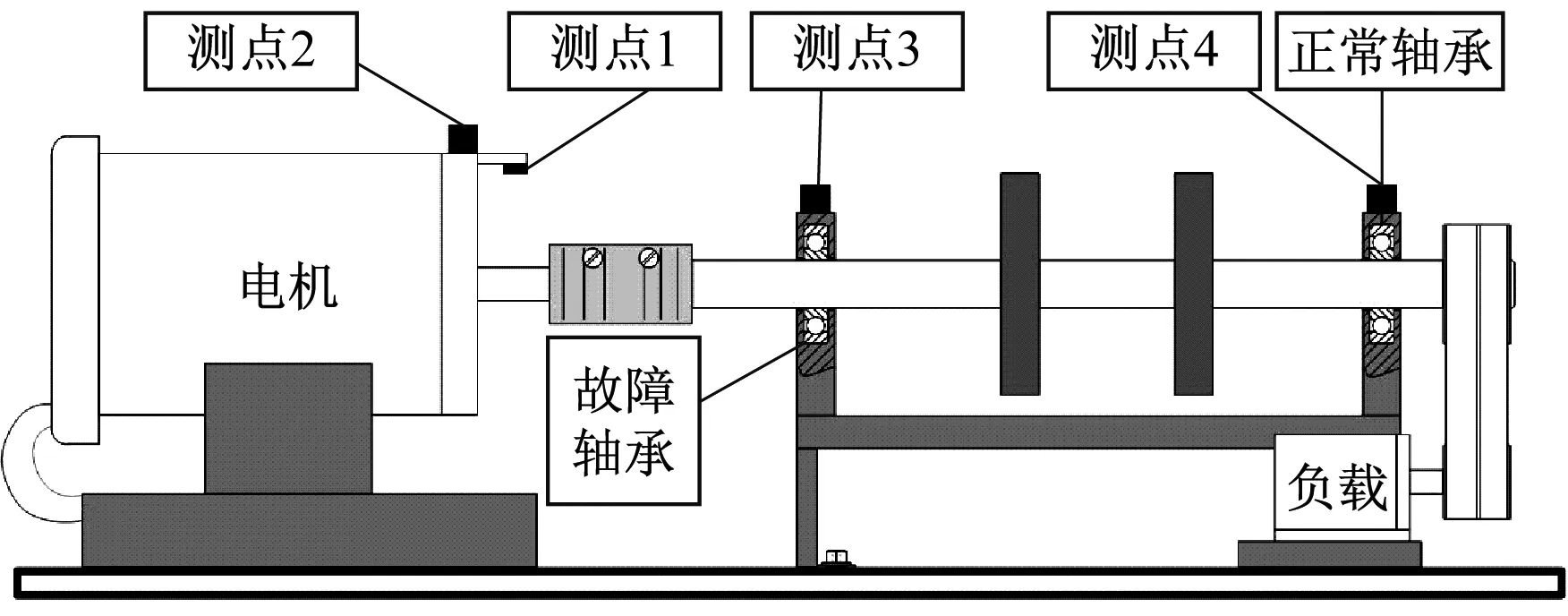
注:测点1为转速计;测点2为电机伸出端轴承;测点3为近电机端轴承;测点4为远电机端轴承。

表1 ER-12K型轴承故障特征频率系数
试验测试的轴承内圈故障信号如图8所示。由于受到高频噪声的干扰,转速信息不容易被提取出来,因此首先对信号进行低通滤波和降采样处理。通过验证发现,低通滤波的截止频率为40 Hz,降采样的间隔为20 ms时提取的瞬时频率效果最好。经过低通滤波处理后,振动信号中的高频成分被去掉,使能量主要集中在低频成分,而降采样也有降噪的作用。信号经处理后,减少了分析的数据量,为瞬时频率脊线的提取节省了时间。

图8 内圈故障振动信号
基于STFT和SST的轴承振动信号时频分布分别如图9~10所示。通过对比发现,与STFT相比,SST具有良好的集中性,提取的脊线也能较好地反映瞬时频率的变化细节。对基于SST提取的脊线进行二阶多项式拟合,得到结果如图11所示。拟合后的脊线能够基本反映出转速的变化趋势。

a) 时频分布

a) 时频分布
通过得到的瞬时频率拟合曲线求取鉴相时标Tn,利用插值法对原振动信号进行角域重采样。图12为基于SST的瞬时频率阶比分析后得到的角域信号,观察角域波形发现具有明显的周期冲击现象。
图13为得到的角域波形做Hilbert包络解调的结果,发现包络阶比谱中阶次1.017、2.024、2.996十分明显,经分析为转频(fr)的1~3倍频。此外,阶次4.979、9.969、14.950也比较突出,与内圈故障特征阶次(li)及其二、三次谐波阶次十分接近,同时还发现lr-li与lr+li阶次,可以断定为明显的内圈故障特征。

图11 SST瞬时频率拟合结果与实际转速对比
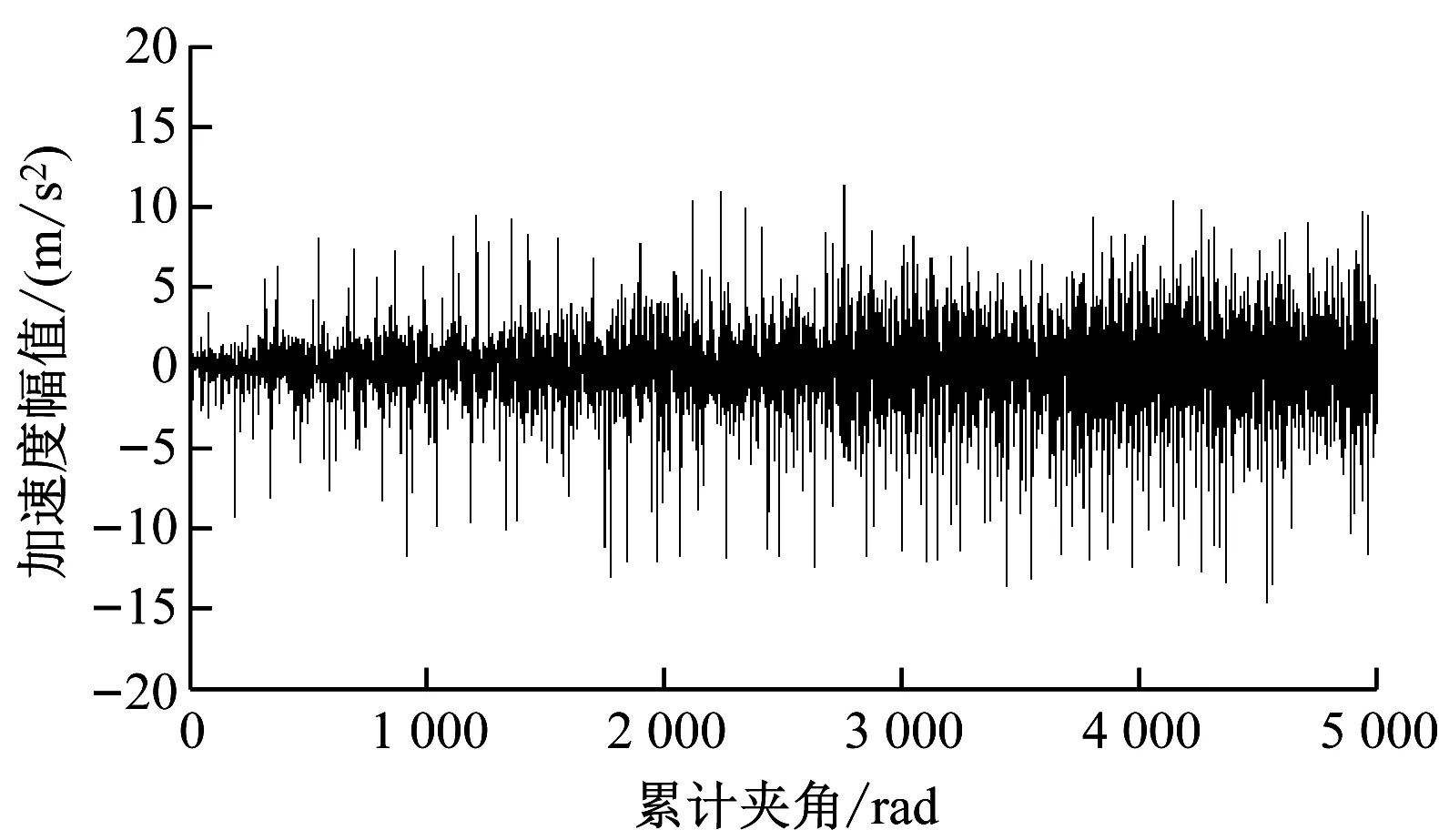
图12 基于SST的瞬时频率阶比角域信号
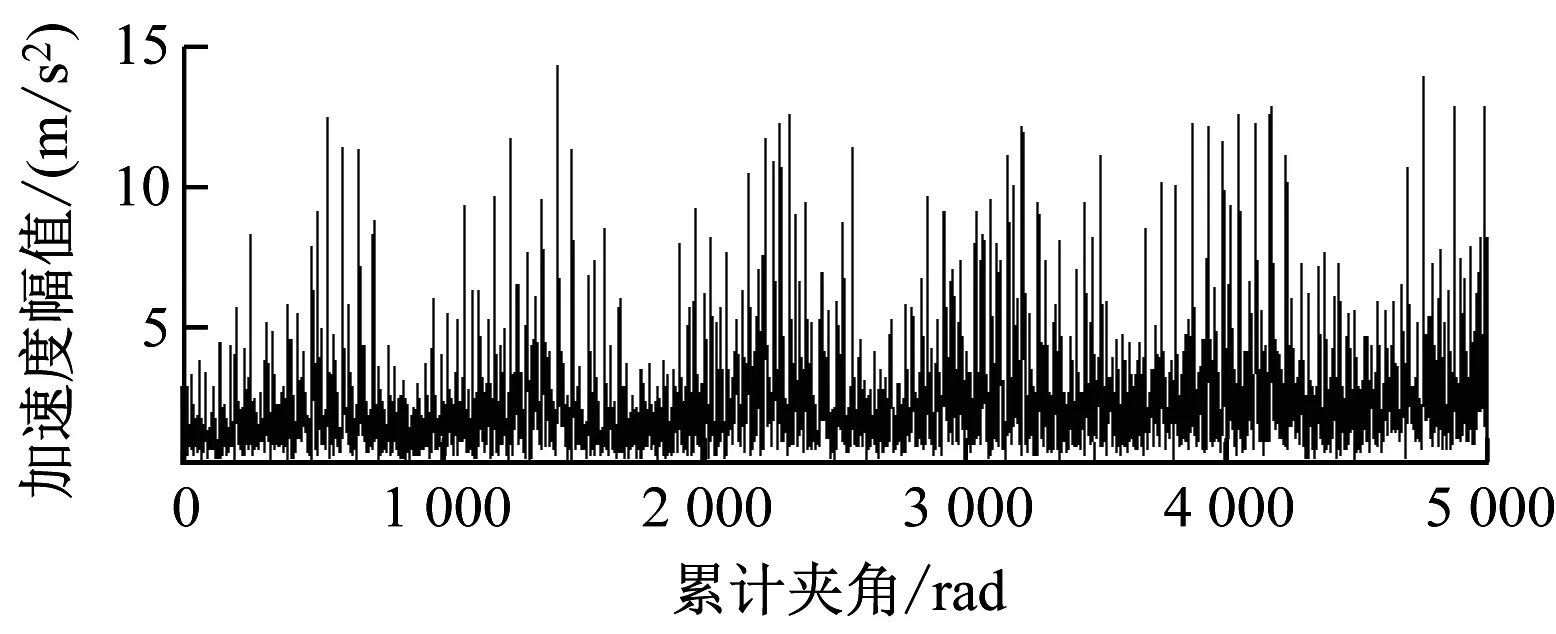
a) 角域信号包络谱

注:fr和fi分别代表转频和内圈的故障特征频率。
通过分析升速过程中的轴承内圈故障振动信号,证明了本文提出的基于SST的阶比分析方法能够有效地提取振动信号中的转速变化曲线,并利用提取的转速变化曲线将非稳态振动信号转化成准稳态角域信号,从而实现阶比分析,成功地诊断出滚动轴承故障。
5 结语
本文提出基于SST的阶比分析法,首先利用SST提取振动信号中的转频曲线,然后利用提取的转频曲线对采集的故障信号进行阶比分析,成功找出了故障特征信息,实现轴承故障诊断。该方法优点如下:
1) SST具有良好的能力集中性,在做时频分析时,能够将时频分布中的能量集中在主要频率曲线上,这为精确地提取转速的瞬时频率提供了有效的理论支持,为阶比分析的成功实现提供了可靠的前提。
2) 与传统的阶比分析方法相比,该方法打破了硬件的局限性,仅通过分析振动信号就能实现对轴承变转速振动信号的阶比分析,完成轴承的故障诊断。其具有安装方便、分析结果准确等优势,大大降低了监测成本,提高了对轴承的故障诊断效率。

