弯-剪-扭复合作用下考虑扭转翘曲的U形薄壁混凝土梁设计方法*
许见超 郭全全 陈圣刚 刁 波 班新林
(1. 中国铁道科学研究院集团有限公司铁道建筑研究所, 100081, 北京; 2. 北京航空航天大学交通科学与工程学院, 100083, 北京; 3. 济南大学土木建筑学院, 250022, 济南∥第一作者, 助理研究员)
U形薄壁混凝土梁可大幅降低建筑物的高度,并具有隔声效果良好、造型美观等优点,在城市轨道交通工程中得到广泛应用[1]。在列车荷载横向偏心力、摇摆力、离心力以及横向风力的作用下,U形梁会受到附加扭矩的影响。U形梁为典型薄壁开口构件,在扭矩作用下会发生约束扭转(同时发生圣维南扭转和翘曲扭转,故又称复合扭转)[2],此时截面上不仅存在引起扭转剪应力的圣维南扭矩Tc和翘曲扭矩Tω,还存在引起翘曲正应力σω的翘曲弯矩Mω。
GB 50010—2010《混凝土结构设计规范》和JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》基于变角空间桁架模型给出了矩形截面、箱型截面和T型截面等闭口截面混凝土构件的圣维南扭转承载力计算公式,但这些公式并未涉及开口截面的计算。GB/T 51234—2017《城市轨道交通桥梁设计规范》给出了U形梁的圣维南扭转承载力计算方法,但未涉及U形梁的扭转翘曲效应。TB 10092—2017《铁路桥涵混凝土结构设计规范》对此无相关规定。综上,现行的混凝土桥涵设计规范针对圣维南扭转给出了构件设计方法,但并未包含考虑扭转翘曲的U形薄壁混凝土梁的扭转设计。
本文基于U形薄壁混凝土梁在弯-剪-扭复合作用下的力学性能研究成果,提出U形薄壁混凝土梁计算Mω和Tω的等效方法,进而提出弯-剪-扭复合作用下U形薄壁混凝土梁考虑扭转翘曲效应的设计方法。
1 U形薄壁混凝土梁的力学性能
1.1 U形薄壁混凝土梁的约束扭转内力和应力
根据Vlasov薄壁开口构件约束扭转弹性理论(以下简称“Vlasov理论”),梁端固支或简支的U形梁的约束扭转内力如图1所示。梁截面上的内扭矩Tin等于Tc和Tω之和,梁端固支和简支时Tc分别在1/4跨度处和支座截面处取得最大值。同时截面上还存在Mω,梁端固支时Mω在跨中和支座截面达到最大值(符号相反),梁端简支时Mω在跨中达到最大值。
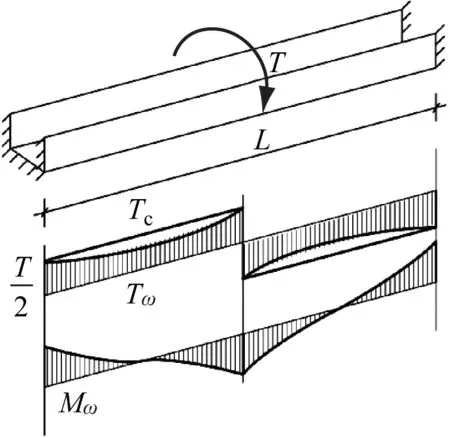
a) 固支梁
梁端固支时的翘曲弯矩最大值Mω1、梁端简支时的翘曲弯矩最大值Mω2的计算式分别为:
Mω1=0.5Tk[cosh(0.5L/k)-1]/
sinh(0.5L/k)
(1)
Mω2=0.5Tksinh(0.5L/k)/cosh(0.5L/k)
(2)
式中:
k——约束扭转特征长度。
约束扭转应力分布如图2所示。圣维南扭转剪应力τc沿U形截面环向流动,翘曲扭矩剪应力τω在两腹板与Tω同向,在底板部分区段与Tω反向;翘曲正应力σω沿U形截面反对称分布。
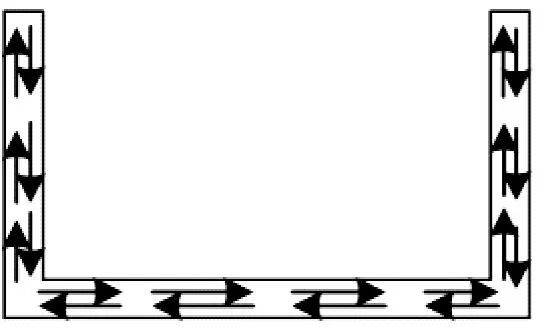
a) τc
1.2 试验研究
本文选取5根1∶4缩尺U形薄壁混凝土梁,编号分别为试件1#、试件2#、试件3#、试件4#、试件5#。梁试件平面图见图3 a),其1-1截面的配筋情况见图3 b)。其中,试件1#~试件4#的纵筋直径为8 mm,试件5#的纵筋直径为10 mm。所有试件的混凝土等级均为C40。
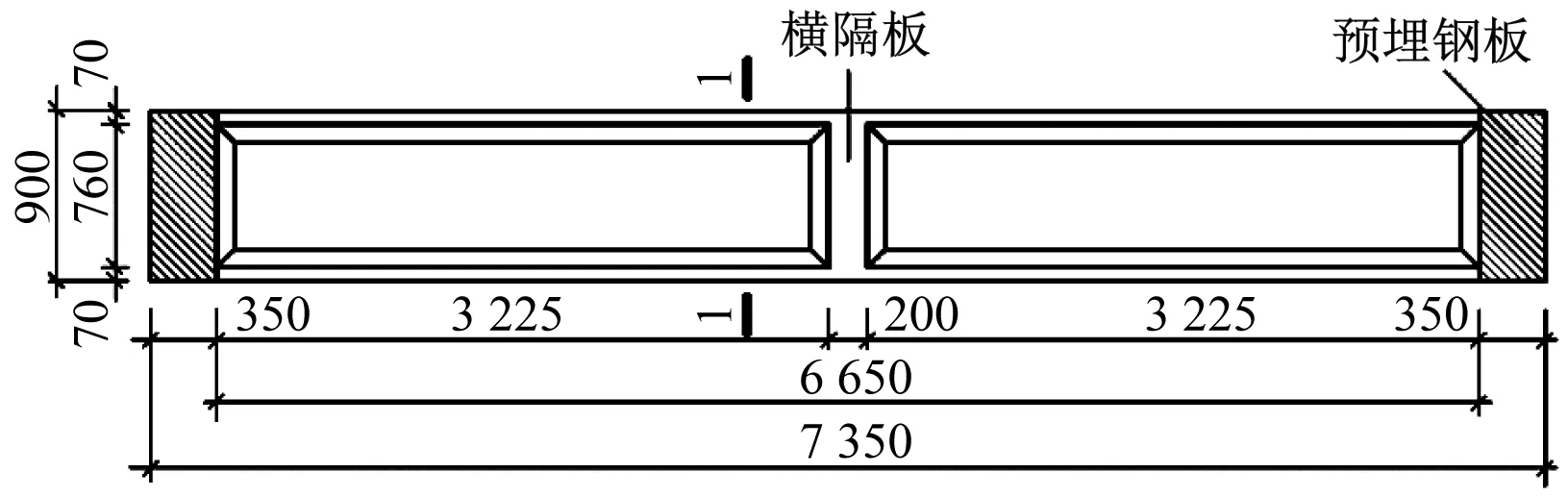
a) 梁试件平面图

b) 1-1截面配筋
分别对这5个试件进行纯扭试验和弯-剪-扭复合加载试验[3-5]。梁试件端部固支,通过2个千斤顶在跨中施加等大反向力实现扭矩加载,通过跨中荷载横向偏心实现弯-剪-扭复合加载。试件在跨中处的T与Mb(弯矩)之比(以下简称“扭弯比”)分别为1∶5、1∶1和1∶0(即纯扭试件)。试件在不同扭弯比下的极限荷载如表1所示。

表1 U形梁试件的极限荷载
试验结果表明,不同扭弯比作用下的U形薄壁混凝土梁试件均发生了适筋弯曲破坏。当扭弯比为1∶5时,弯曲破坏由Mb主导,两腹板同向弯曲,弯曲应力σb和较小的σω在加载侧(距荷载较近)腹板处叠加,致使加载侧腹板跨中截面发生底部受拉、顶部受压的适筋弯曲破坏。当扭弯比为1∶1时,弯曲破坏由Mb和Mω共同主导,Mb和Mω产生的正应力大小相当,二者在加载侧腹板处叠加产生弯曲破坏,在非加载(距荷载较远)侧腹板处则相互抵消、处于低应力状态。当扭弯比为1∶0时,破坏由Mω主导,两腹板反向弯曲,此时跨中和支座截面处的Mω大小相等,跨中截面和支座截面均发生弯曲破坏。
1.3 数值模拟分析
基于试验研究结果[6-7],本文利用有限元数值模型,选取了边界条件、跨高比以及纵筋-箍筋配筋强度比3个关键参数,对U形薄壁混凝土梁的受力性能进行系统研究,取得以下主要结论:
1) 纯扭矩作用下,在跨高比逐渐增加的过程中,梁端固支U形梁的破坏模式由Tω主导的剪切型破坏(跨高比为8~10时)演变为由Mω主导的弯曲破坏(跨高比为12~16时),再演变为弯曲-剪切破坏(跨高比为18~20时Mω主导的弯曲破坏和Tc主导的剪切型破坏同时发生)。当梁端简支时,随着跨高比变化,上述破坏过程的演变速度更快。
2) 在弯-剪-扭复合作用下,随着扭弯比的增加,U形梁破坏模式的变化趋势为由弯曲破坏向剪切型破坏转变。在已有工程应用中,连续U形梁的跨高比一般为13~15,此时任意扭弯比作用下均会发生弯曲破坏;简支U形梁的跨高比一般为10~12,此时扭弯比小于1∶2时会发生弯曲破坏,扭弯比大于1∶2时会发生弯曲-剪切破坏。
1.4 极限状态内力分析和承载力计算
基于弯-剪-扭复合作用下U形薄壁混凝土梁的试验研究和有限元参数分析结果,本文进一步进行极限状态内力分析和承载力计算,设V为截面剪力。如图4 a)所示,将半U截面上的σω积分为等效弯矩Meq和轴力Neq,即将Mω等效为作用在半U截面上的Meq和Neq;如图4 b)所示,将Tω等效为作用在两腹板上的剪力Vω。在弯-剪-扭复合作用下,弯曲破坏发生在Mb和Mω取最大值跨度位置的加载侧半U截面处,其相应的内力为Neq、合成弯矩(Meq+Mb/2)以及合成剪力(V/2+Vω)。剪切型破坏发生在Tc取最大值跨度位置的加载侧腹板处,其相应的内力为(Wtw/Wt)Tc(Wtw为腹板受扭塑性抵抗矩,Wt为U形截面受扭塑性抵抗矩),以及合成剪力(V/2+Vω)。

a) 等效弯矩和轴力
考虑到U形梁腹板上分布纵筋较多,加载侧半U截面的正截面轴力-弯矩承载力计算可根据剪力墙正截面承载力计算方法进行,具体可见文献[3]。加载侧腹板的抗剪和扭-剪承载力根据变角空间塑性桁架理论进行计算。对于任意特定扭弯比加载工况,其截面内力扭矩-弯矩-剪力比例一定,分别在弯曲破坏危险截面处和剪切型破坏危险截面处令截面内力等于截面承载力,可计算得到发生弯曲破坏和剪切型破坏的外荷载Pf和Ps,这2种破坏外荷载的较小值即为真实极限荷载计算值,相应的破坏模式为真实破坏模式。经与试验及数值模拟分析结果对比,三者相互吻合良好。
2 U形薄壁混凝土梁设计方法
2.1 内力分析
内力分析的关键为约束扭转内力分析,采用上文所述的内力等效方法。具体步骤为根据U形梁支撑条件和外荷载分布,采用Vlasov理论进行约束扭转内力计算,再将Mω在弯曲破坏危险加载侧半U截面上等效为弯矩Meq和轴力Neq,在剪切破坏危险加载侧腹板上将Tω等效为剪力Vω。叠加截面上的弯矩和剪力后即得设计内力。
2.2 承载力设计
基于内力分析结果进行承载力设计,对于加载侧半U截面,其正截面承载力计算采用上文1.4节的计算方法。对于加载侧腹板的抗剪和扭-剪承载力计算,采用现行《城市轨道交通桥梁设计规范》方法。
相比现行规范,本文设计方法的关键点在于采用U形薄壁梁的约束扭转内力并进行等效,而不是忽略U形薄壁梁的翘曲扭转效应。
3 是否考虑扭转翘曲的设计内力和极限荷载计算值差异分析
3.1 设计内力对比
本文以在试验梁试件跨中作用1 kN·m的外扭矩为例进行分析。跨中加载侧半U截面以及1/4跨度处加载侧腹板的设计内力如表2~3所示。由表2~3可以看出,是否考虑扭转翘曲所得到的设计内力在内力类别和数值上均有差异显著。
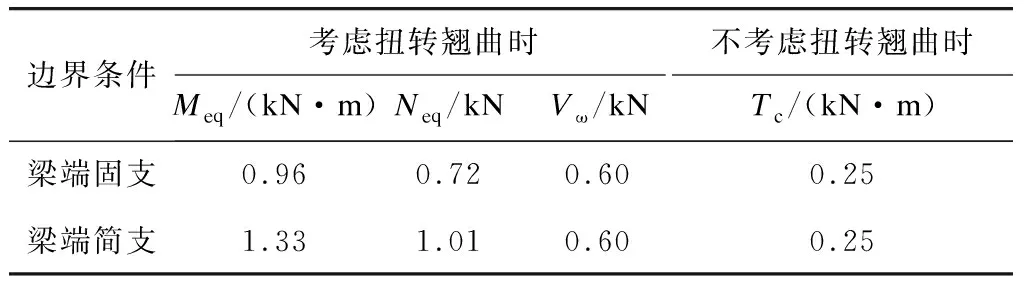
表2 U形梁加载侧半U截面的设计内力计算结果

表3 U形梁加载侧腹板的设计内力计算结果
3.2 极限荷载计算值对比
以试件2#的几何、材料和边界参数为例,分别计算考虑扭转翘曲、忽略扭转翘曲2种情况下试件的极限荷载。如图5所示,V与Mb的关系为:Mb=VL/4。从图5可知,当扭弯比较小(约小于1∶8)时,忽略扭转翘曲的极限荷载计算值偏高,即偏于危险;当扭弯比较大(约大于1∶8)时,忽略扭转翘曲的极限荷载计算值偏小;纯扭转(扭弯比为1∶0)时,考虑扭转翘曲的极限扭矩计算值为133.4 kN·m,而忽略翘曲的极限扭矩计算值为53.4 kN·m,二者差异巨大。

图5 U形梁极限荷载的计算结果
4 结论
1) 扭转翘曲所得到的设计内力结果在内力类别和数值上均差异显著,U形薄壁混凝土梁的设计应考虑扭转翘曲的影响。
2) 当扭弯比较小(约小于1∶8)时,忽略扭转翘曲时得到的极限荷载计算值偏大;当扭弯比较大(约大于1∶8)时,不考虑扭转翘曲时得到的极限荷载计算值偏小。

