中低速磁浮列车悬浮控制系统可靠性分析及优化*
侯 磊 张文跃 高 锋 梁 涛
(1.中车株洲电力机车有限公司, 412001, 株洲; 2.中国铁建电气化局集团第四工程有限公司,410007, 长沙∥第一作者, 工程师)
目前,轨道交通领域中的地铁、轻轨、高速铁路等模式下的列车技术相对成熟,对列车可靠性的研究较为充分[1-3],而中低速磁浮作为新兴的交通模式,其运营的车辆数量少、时间短、数据积累不足,因此对中低速磁浮的列车可靠性研究较少;尤其是对中低速磁浮列车的核心系统——悬浮控制系统的可靠性评估、分析、优化较为缺乏。为了抓住磁浮交通大发展的契机,促进中低速磁浮的推广应用,本文依据积累的实际运营数据,结合悬浮控制系统的组成结构,对其系统的可靠性进行评估,对系统的薄弱点进行优化,从而提升系统的可靠性。
1 悬浮控制系统的结构和可靠性模型
本文以中低速磁浮列车的悬浮控制系统为研究对象,基于其结构组成,采用串联、并联系统等可靠性模型对其进行分析。
1.1 悬浮控制系统的结构
中低速磁浮列车的悬浮控制系统用于实现列车稳定悬浮,是列车的核心子系统,直接影响列车运行的稳定性和可靠性。
如图1所示,中低速磁浮列车有多个悬浮点位,且各悬浮点位的组成结构相同,整车的悬浮控制系统包括整列车所有悬浮点位的悬浮控制单元。单个悬浮点位的悬浮控制单元主要由1台悬浮控制器和1台悬浮传感器组成。
1.2 悬浮控制系统的可靠性模型
中低速磁浮列车由若干节车辆编组而成。以1节中低速磁浮车辆进行可靠性建模分析,其共有10台悬浮电磁铁,每台悬浮电磁铁由2个悬浮点位的悬浮控制单元共同控制,1节车共包含20个悬浮点位的悬浮控制单元。当某个悬浮控制单元故障时,为了避免悬浮电磁铁线圈中电流过大,导致线圈烧损,同一台悬浮电磁铁的另外1个悬浮点位的悬浮控制单元必须封锁输出,即控制同一台悬浮电磁铁的2个悬浮控制单元可视为同时失效。
此外,由于不同悬浮电磁铁的悬浮控制单元相互独立,为并联关系,因此,1节车的悬浮控制系统可靠性模型可视为串并联混合模型,如图2所示。
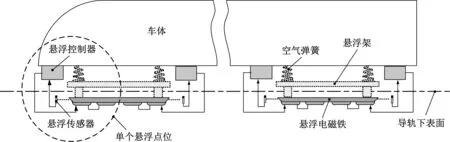
图1 中低速磁浮列车悬浮控制系统结构示意图
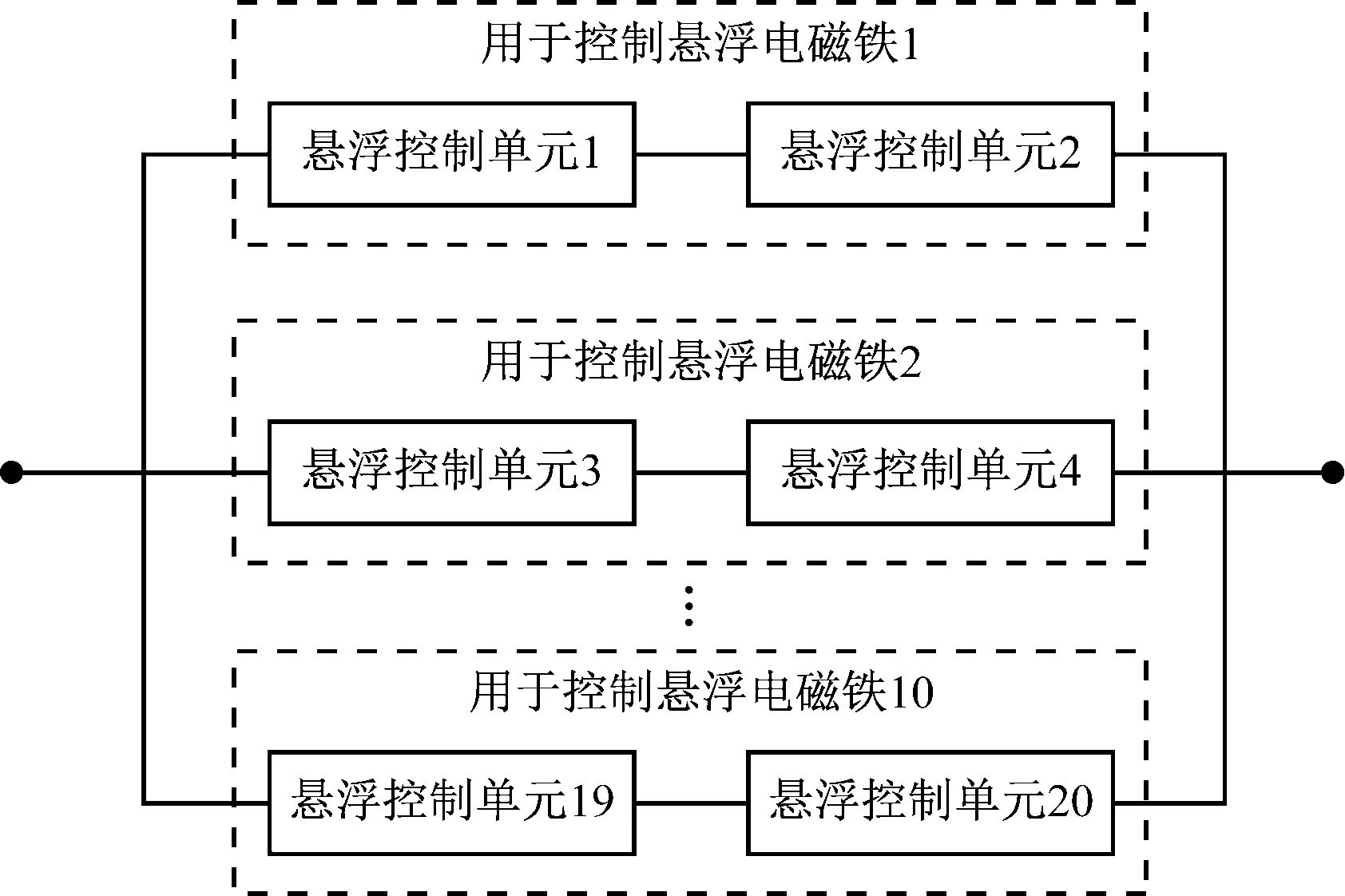
图2 1节中低速磁浮车辆的悬浮控制系统可靠性模型
对于单个悬浮点位的悬浮控制单元,依据电路结构分析,悬浮传感器以及悬浮控制器内部的控制电源、悬浮控制板、信号处理板等主要部件中任意部件故障都会引起整个悬浮控制单元故障,因此悬浮控制单元的可靠性模型应为串联模型,如图3所示。

注:IO为输入输出;IGBT为绝缘栅双极型晶体管。图3 悬浮控制单元的可靠性模型
2 可靠性数学模型
2.1 电子产品的可靠性数学模型
电子产品的寿命一般服从指数分布,特征是无记忆性,即前后发生的2个故障之间不存在联系。其可靠性函数R(t)的计算式为:
R(t)=e-λt
(1)
式中:
t——工作时间;
λ——故障率。
可修复产品的寿命为相邻2次故障间的工作时间,其平均寿命即平均无故障间隔时间为:
(2)
从式(2)中可知,TMTBF是λ的倒数。
2.2 串联、并联系统的可靠性数学模型
假设某系统中有n个相互独立的单元,每个单元的可靠性为Ri(t)(i=1,2,…,n),则该串联系统的可靠性Rs,s(t)为:
(3)
依据式(1)得:
Ri(t)=e-λit
(4)
Rs,s(t)=e-λst
(5)
则串联系统故障率λs,s(t)为:
(6)
依据式(2),串联系统的平均无故障间隔时间Ts,MTBF为:
(7)
类似串联系统,并联系统的可靠性Rp,s(t)为:
(8)
并联系统的故障率λp,s(t)为:
(9)
2.3 悬浮控制系统的可靠性数学模型
根据故障严重等级,中低速磁浮列车的故障形式可分为以下3类:
1) 救援故障:列车无法继续运营,必须进行救援。根据运营经验,当1节车10台悬浮电磁铁中有5台及以上的悬浮控制单元失效时,列车必须救援。
2) 晚点故障:列车可以降速运行,不需要救援,但会发生晚点。当1节车10台悬浮电磁铁中有5台以下的悬浮控制单元失效时,列车需降速运行。
3) 一般故障:悬浮控制系统中的部件发生轻微故障,未完全失效,不影响运营,列车运营结束后,回库进行检修。
r/n(G)表决模型用于任务可靠性建模[4]。如图4所示,1节车的悬浮控制系统表决模型由10台悬浮电磁铁及1个表决器组成,采用5/10(G)表决器,当正常运行的悬浮电磁铁数量不小于5台时,表决器将做出判断,系统不会发生救援故障。
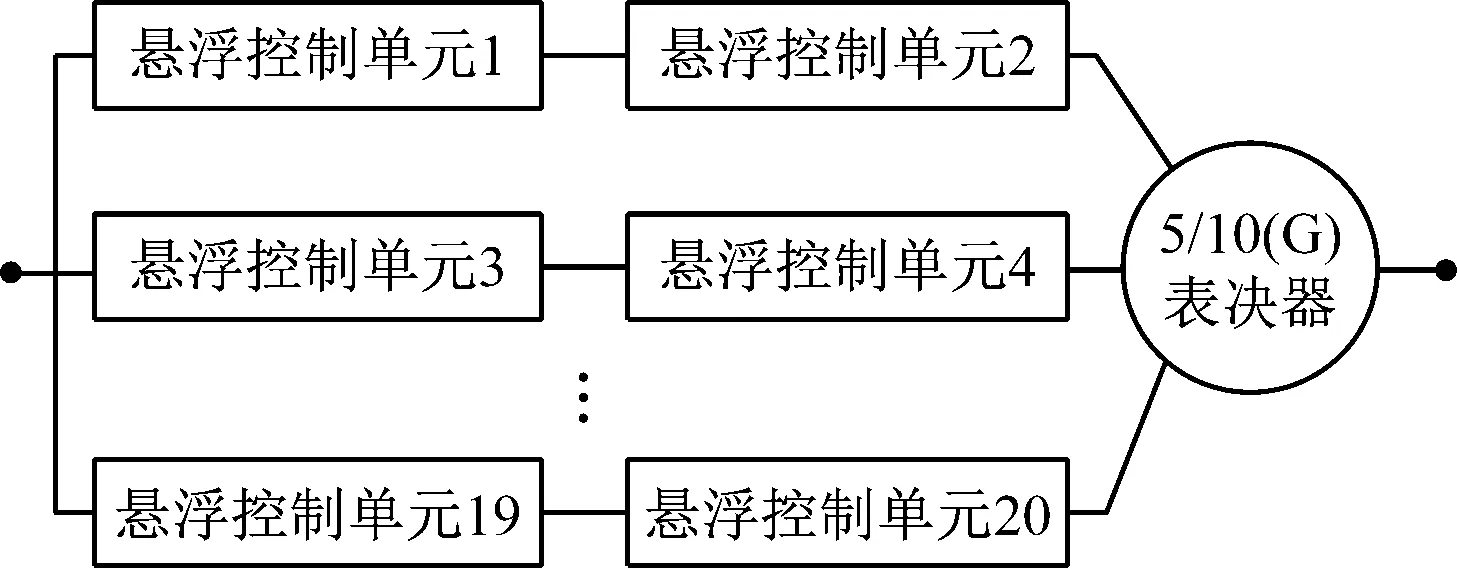
图4 1节中低速磁浮车辆悬浮控制系统的表决模型
R(t)为单个悬浮控制单元的可靠性,则每组的可靠性为R(t)2。依据文献[4]可得1节车的悬浮控制系统可靠性Ra,s(t)为:
(10)
式中:

3 悬浮控制系统的可靠性计算与优化
3.1 各部件的可靠性计算
由于仅有一部分部件在运营过程中出现故障,仅基于运营数据无法计算出悬浮控制系统所有部件的可靠性,因此针对运营过程中未发生故障的部件,本文结合标准数据和经验数据对其可靠性进行了分析和计算。
3.1.1 基于运营数据计算部分部件的故障率
以悬浮控制系统及其组成部件区间估计TMTBF的单侧置信下限θL为:
(11)
式中:
Ta——运营总时间;
R——故障次数;

γ——置信水平(取0.75)。
选取某中低速磁浮线路4年的运营数据进行分析。该线路共有4列3节编组的列车,每列车有60个悬浮控制单元。该线路每日运营时间为18 h,4年累计运营总时间Ta为630 720 0 h。该线4年内所有列车的悬浮控制系统共发生了15起故障(见表1),根据可靠性理论,综合Ta、表1数据、θL以及图2~3的可靠性模型,可计算出表1中各部件的故障率。

表1 某中低速磁浮线路所有列车的悬浮控制系统故障数据
3.1.2 参考标准数据计算部分部件的故障率
对于常见的电子元器件(如温度开关、电源滤波器、支撑电容等),通过查阅GJB/Z 299C—2006《电子设备可靠性预计手册》可得到其通用故障率,进而计算其故障率。
3.1.3 结合经验数据计算部分部件的故障率
对于电压传感器、电流传感器、IGBT电路、接触器等部件,根据经验数据,可估算出其故障率。
3.1.4 悬浮控制单元的主要部件故障率计算值
综合上述运营数据、标准数据和经验数据的分析与计算,可得悬浮控制单元的主要部件的故障率计算值如表2所示。其中:序号1~8部件的故障率为基于运营数据的计算值;序号9~11部件的故障率为参考标准数据查表得到的计算值;序号12~15部件的故障率为结合经验数据得到的计算值。
依据式(6),由表2可得单个悬浮控制单元故障率计算值为2.475×10-6。
3.2 可靠性的优化设计
从表2中可知,悬浮传感器、斩波管理板、斩波驱动板等部件的故障率较高,是影响悬浮控制单元可靠性的薄弱环节。结合结构设计经验,本文提出的可靠性优化设计措施包括:
1) 悬浮传感器的优化设计。通过在悬浮传感器内部增加1个间隙探头和1路独立供电电源,进一步提高悬浮传感器的冗余能力。依据可靠性理论进行计算,优化后的可靠性较优化前提升了67%。
2) 斩波驱动板的优化设计。将斩波器电源滤波电容由钽电容更换为瓷片电容,电容量保持不变。经实际验证,更换斩波器电源滤波电容后,1年内未发生过类似故障。考虑到斩波驱动板与信号处理板电路结构相似、内部器件数量接近,可认为优化后的斩波驱动板与表2中的信号处理板故障率相当。

表2 悬浮控制单元的主要部件故障率计算值
3) 斩波管理板的优化设计。增加供电电源的隔离和滤波处理,提升其抗电磁干扰能力。
4) 控制电源的优化设计。重新设计控制电源,对电源进行降额设计,以提高电源的可靠性。
优化前后的各部件故障率对比如表3所示。

表3 优化前后的各部件故障率
依据式(6),与优化前相比,优化后的悬浮控制单元故障率为1.873×10-6,降幅为24.32%。
4 可靠性优化前后对比分析
4.1 救援故障对比分析
结合表2~3可得优化前后悬浮控制单元的故障率分别为2.475×10-6和1.873×10-6,分别计算其在每日运营时间18 h下的可靠性,所得结果都极为接近1,即优化前后出现救援故障的概率都极低。
4.2 晚点故障对比分析
由悬浮控制系统造成的列车晚点故障一般可分为掉点故障、砸轨故障和过流故障3种。
1) 掉点故障分析。悬浮掉点指该悬浮点位不能悬浮,悬浮控制单元无输出,列车需降速运行,从而造成列车晚点。根据悬浮控制单元的工作原理,控制电源、接触器、电源滤波器、支撑电容、IO板、悬浮控制板、斩波管理板、斩波驱动板、IGBT电路、陶瓷保险丝等部件发生故障都可能造成掉点故障,因此,掉点故障的故障率为这些部件故障率之和。依据表2~3,可知优化前后因掉点故障引起的列车晚点故障率分别为1.853×10-6和1.429×10-6。
2) 砸轨故障分析。砸轨是指悬浮发生失稳,电磁铁与轨道之间发生持续撞击,此时需通过列车降速以保障乘客的安全,从而引起列车晚点。根据悬浮控制单元的工作原理,悬浮控制板、信号处理板、IO接口板、斩波管理板等部件发生故障都可能引起砸轨故障,因此,砸轨故障的故障率为这些部件故障率之和。依据表2~3,可知优化前后因砸轨故障引起的列车晚点故障率分别为0.673×10-6和0.620×10-6。
3) 过流故障分析。过流是指由于输出短路等原因造成悬浮控制单元输出电流持续超过安全阈值,此时必须关闭输出,同时通过降速以保障乘客的乘坐舒适度,从而引起列车晚点。根据悬浮控制单元的工作原理,电源滤波器、电流传感器、悬浮控制板、IGBT电路、斩波管理板、斩波驱动板等部件发生故障都可能造成过流,因此,过流故障的故障率为这些部件故障率之和。依据表2~3,可知优化前后因过流故障引起的列车晚点故障率分别为1.313×10-6和0.904×10-6。
根据实际经验,以上3类故障发生概率占比分别为0.4,0.3和0.3,因此,悬浮控制器晚点故障的故障率预计值λ晚点为:
λ晚点=0.4λ掉点+0.3λ砸轨+0.3λ过流
(12)
式中:
λ掉点——发生掉点故障的故障率;
λ砸轨——发生砸轨故障的故障率;
λ过流——发生过流故障的故障率。
依据上述计算方法,并查表2~3中优化前后相关部件的故障率,可计算得到优化前后悬浮控制器的晚点故障率分别为1.337×10-6和1.029×10-6。
依据式(1),可得晚点故障发生的概率Y为:
Y=1-R(t)=1-e-λt
(13)
将上述优化前后的晚点故障率代入式(13)中,可得到优化前后晚点故障发生的概率对比情况,如图5所示。
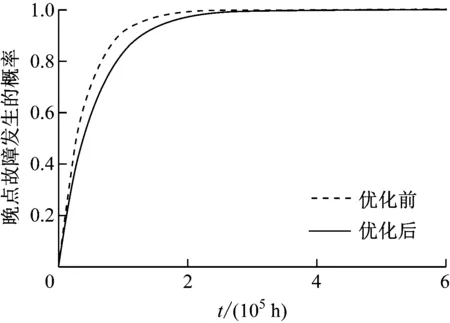
图5 优化前后晚点故障发生的概率
4.3 一般故障对比分析
悬浮控制单元中任意1个元器件发生故障都会造成一般故障,这类故障虽不影响列车的正常运行,但需要列检、临修时进行处理,因此该类故障的故障率之和即为悬浮控制单元的故障率。可将表2~3中的数据进行求和计算,得到优化前后悬浮控制单元的故障率分别为2.475×10-6和1.873×10-6。
将优化前后悬浮控制单元的故障率代入到式(1)中,可得到优化前后的悬浮控制单元的可靠性变化曲线,如图6所示。将优化前后悬浮控制单元的故障率代入到式(1)和式(10)中,可得到优化前后1节车的悬浮控制系统的可靠性变化曲线,如图7所示。
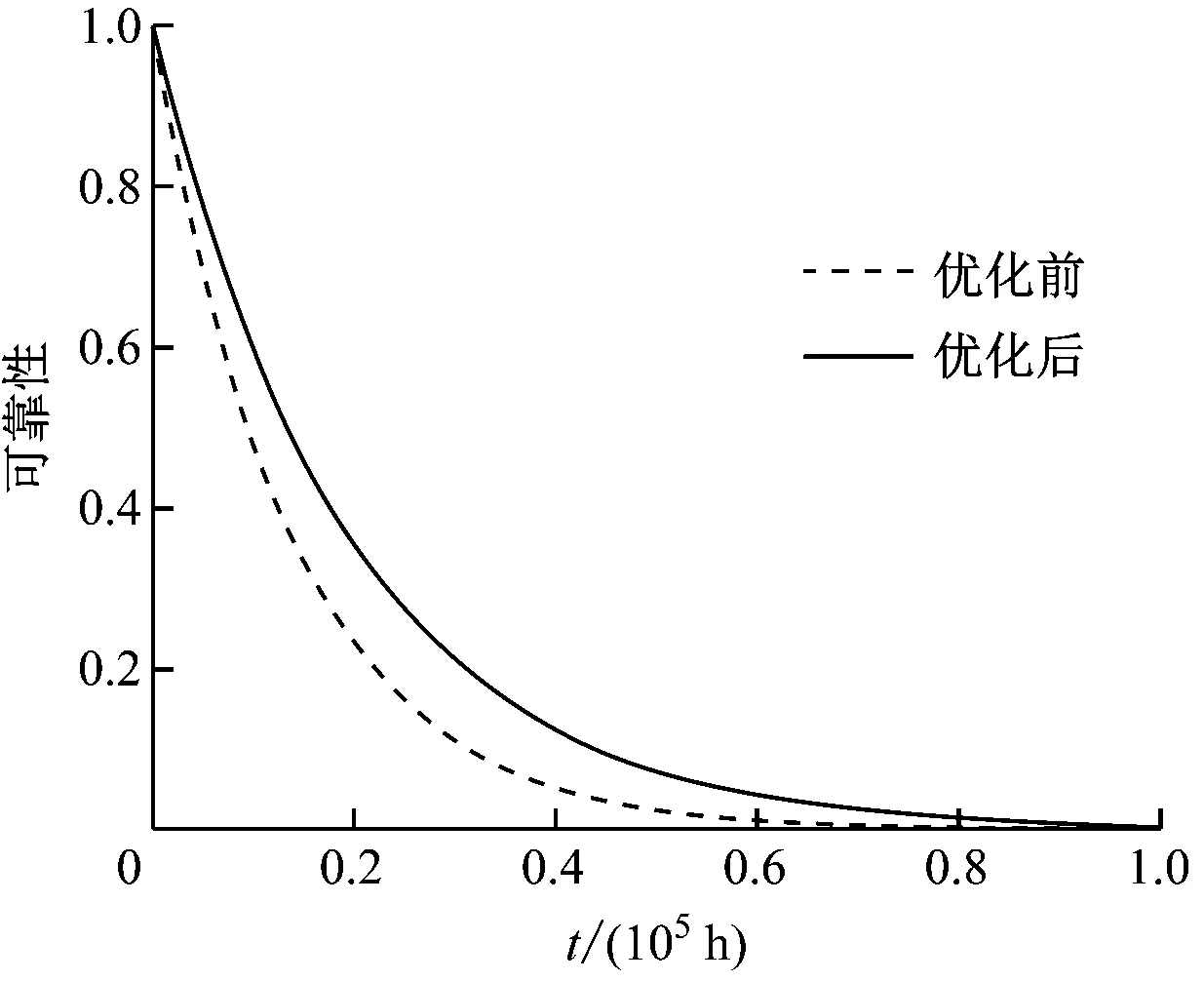
图6 优化前后悬浮控制单元的可靠性

图7 优化前后1节车悬浮控制系统的可靠性
5 结语
本文针对中低速磁浮交通这一前景广阔的新兴轨道交通模式,研究了业内目前较少涉及、但直接影响运营的悬浮控制系统可靠性问题。基于运营数据、标准数据和经验数据,结合控制系统的组成结构和相关的可靠性模型,在找出悬浮控制系统可靠性薄弱环节的基础上,对悬浮控制系统的主要部件进行了优化,并分析对比了优化前后各个部分对系统可靠性的影响,可为中低速磁浮列车的可靠性提升提供指导。

