齿轨铁路的线路设计参数研究*
王 飞
(1.轨道交通工程信息化国家重点实验室(中铁一院), 710043, 西安; 2.陕西省铁道及地下交通工程重点实验室(中铁一院), 710043, 西安∥工程师)
齿轨铁路是国内引进服务于地形起伏较大的山地城市/景区的交通系统,可服务于国家新型城镇化建设及“交通+旅游”融合发展战略。我国在客运齿轨铁路方面的研究尚属空白。本文结合张家界七星山观光火车项目的初步设计,对齿轨铁路的线路主要设计参数进行初步探究。
1 研究基础
1.1 概述
齿轨铁路选用齿轨车辆,采用齿轮齿条传动。其与普通的铁路线路最大的区别在于在普通路轨间加装了齿条,通过齿轨机车的齿轮与齿条啮合力提供走行动力,有效克服了普通铁路线路轮轨黏着力不足的问题。因此,齿轨铁路的线路爬坡能力较强。目前,国外已建成的齿轨铁路近180条[1],有着丰富的应用实例,轨道形式有7种,轨距多为800~1 422 mm;齿轨车辆上下坡的最高速度可分别达到40 km/h和30 km/h;线路最大坡度为25%~48%。
1.2 张家界七星山观光火车项目基础参数
张家界七星山观光火车项目是国内第1条采用齿轨铁路承担景区游客旅游观光及景区人员通勤的交通线路,线路全长8.4 km[2]。该项目采用的齿轨车辆由国内自主研发,其编组形式采用“Mc(带司机室动车)+M(齿轨动车)+Mc(带司机室动车)”方式;齿轨采用strub系统,即只采用1条较宽的齿条。车辆总体设计参数见表1。
2 齿轨铁路线路平面设计参数研究
如图1所示,齿轨车辆牵引动力主要依托齿轮驱动,扭矩为M,c为牵引点高度,b为轴距,θ为坡度角。前后轮牵引力F1、F2与牵引阻力F实现坡面纵向平衡。重力W与前后轮支撑力N1、N2实现坡面垂向平衡。齿轨车辆的齿轮与齿条啮合的有关力系也实现平衡,故在平面设计参数研究时暂简化齿轮与齿条的接触关系。
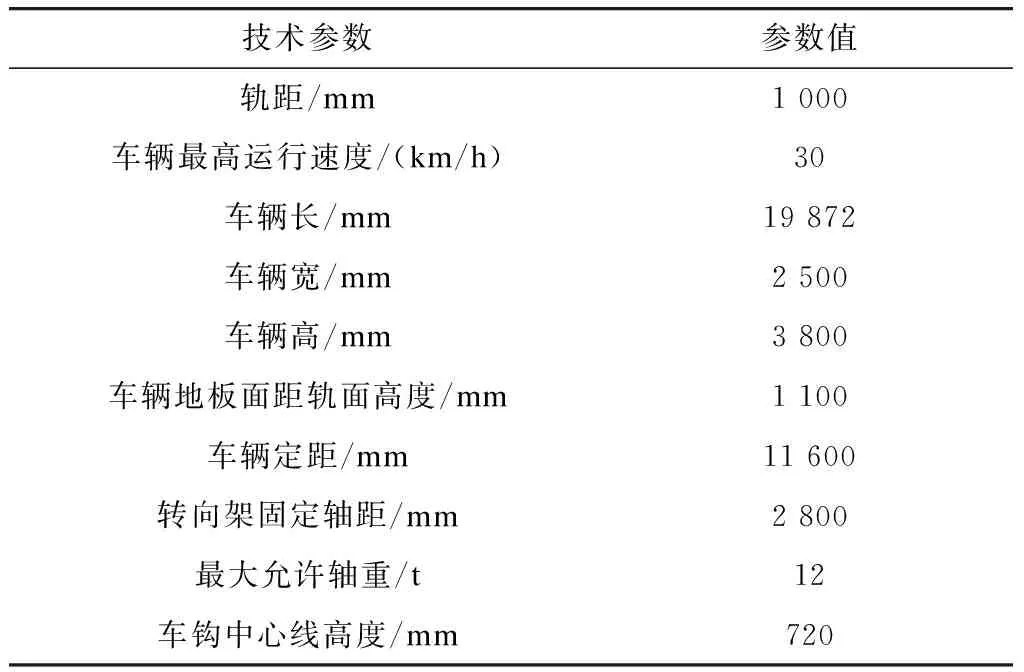
表1 张家界七星山观光火车项目车辆主要技术参数
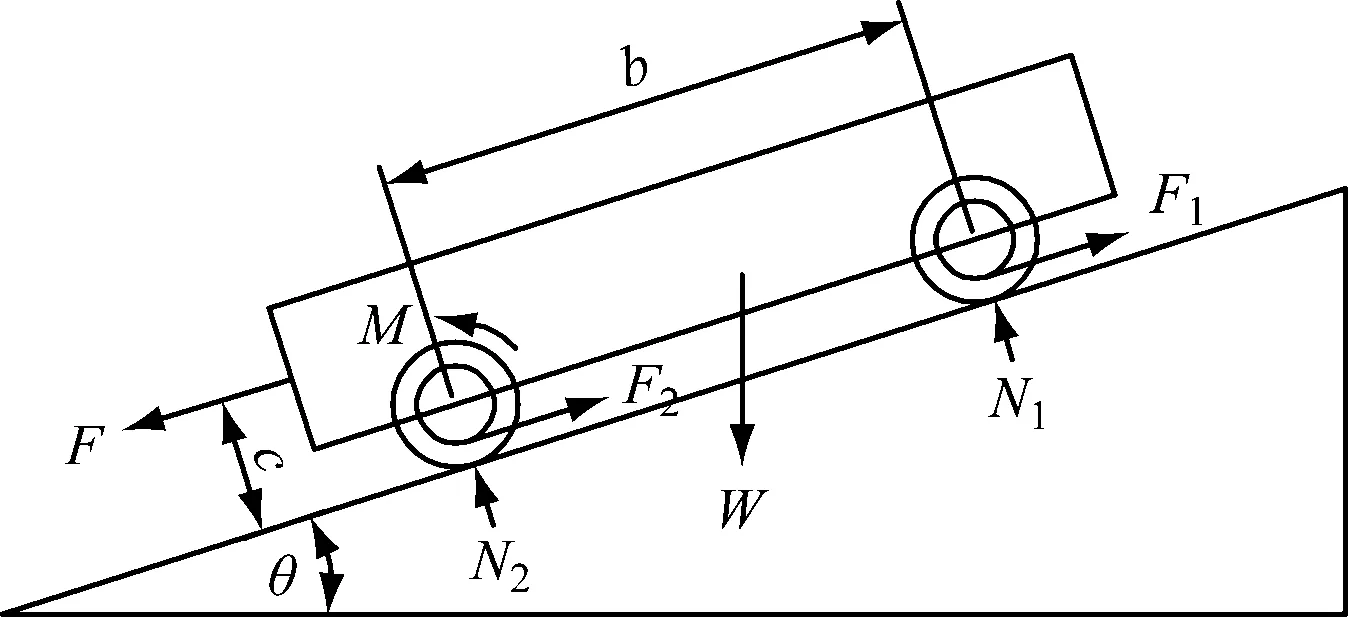
图1 齿轨车辆纵向受力示意图
2.1 曲线外轨超高
参考国外铁路设计资料,米轨铁路可采用50 kg/m标准轨,轨头宽70 mm[3],则两股钢轨轨头中心距S1为1 070 mm。按照外轨超高与圆曲线半径关系,齿轨铁路曲线外轨超高值的计算式为:
h=8.4v2/R
(1)
式中:
h——外轨超高值,mm;
v——列车通过速度,km/h;
R——圆曲线半径,m。
2.1.1 设计最大外轨超高允许值hmax
列车通过或停在曲线时,其所受的合力作用点应落在车轮支承点内,此时可保证车辆稳定和行车安全。如图2所示,H为车体重心C至轨顶面高度估算值,轨顶连线为BA,对应的内外轨超高分别为0、hmax;未被平衡超高Δh引起的合力未通过轨道中心O,由此产生了偏心距e。
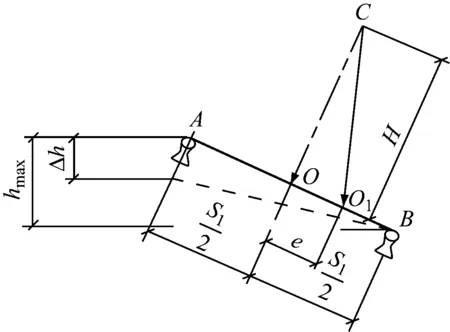
图2 外轨最大超高计算示意图
车辆稳定度采用稳定系数n表示。n在一般条件下不应小于3,其计算式为:
n=S1/(2e)
(2)
结合图2的几何关系,可得e的计算式为:
e=HΔh/S1
(3)
根据式(2)、(3)的计算,当列车在曲线上停车时,超高全是过超高,此时n取3,H为1 200 mm(容许设置的最大超高为159 mm)。考虑风力、车辆状态不良等因素,综合齿轨线路的运营维护实际及项目特点,n的取值不大于5.5,计算得到hmax为85 mm。
2.1.2 欠超高允许值hq
考虑旅客乘坐舒适度的计算式为:
hq=S1aL/g
(4)
式中:
aL——未被平衡的离心加速度,m/s2;
g——重力加速度,m/s2。
国内轨道交通经大量实践,规定aL不得超过0.30~0.65 m/s2,最大取值为1.0 m/s2。对于齿轨线路,参考一般条件(保证旅客良好的乘坐舒适度的线路条件)下取aL为0.40 m/s2,困难条件(保证旅客的乘坐舒适度满足最基本要求的线路条件)下取aL为0.60 m/s2。按式(4)计算,hq在一般条件时取40 mm,在困难条件时下取60 mm。
2.1.3 过超高允许值hg
齿轨车辆的轴重小,牵引质量单一,过超高时对乘客舒适度的影响与欠超高相同,因此hg的取值与hq相同。
2.1.4 超高限值
结合乘坐舒适度条件,设计超高与欠超高之和的允许值在一般条件时取140 mm,困难条件时取160 mm。欠超高与过超高之和的允许值一般条件时取100 mm,在困难条件时取120 mm。
2.2 平面曲线半径
2.2.1 最小曲线半径
2.2.1.1 满足舒适度条件的最小曲线半径
受齿轮与齿条的机械磨损及上下行车辆高低速运行要求的影响,齿轨线路需要考虑不同速度列车共线运营的条件,其最小曲线半径的计算式为:
(5)
式中:
Rmin——高低速匹配时的最小曲线半径,m;
vmax——设计最高速度,km/h;
vmin——列车最小旅行速度,km/h。
结合齿轨车辆参数及国外的运营实践,vmax取30 km/h,vmin按5 km/h考虑。根据超高限值及式(5),计算取整后得到最小曲线半径在一般条件时不小于75 m,在困难条件时不小于65 m。
2.2.1.2 满足车辆安全运行的最小曲线半径
为满足齿轨车辆的安全运行,避免齿轨啮合不良等安全隐患,根据目前齿轨车辆构造的要求,齿轨线路最小曲线半径在一般条件下不小于120 m,在困难条件时不小于90 m。
综上,齿轨铁路设计最小曲线半径在一般条件时不小于120 m,在困难条件时不小于90 m。
2.2.2 最大曲线半径
结合传统轮轨交通线路测量及养护维修经验,考虑齿条制造工艺,齿轨铁路的线路最大曲线半径不宜大于5 000 m。
2.3 缓和曲线
2.3.1 线型选用
比对国外齿轨铁路及国内轮轨线路的设计经验[4],缓和曲线线型采用线形简单、设计方便、长度短且易于铺设养护的直线超高顺坡三次抛物线形式。
2.3.2 缓和曲线长度
2.3.2.1 安全指标
齿轨铁路缓和曲线的取值应不致使车轮脱轨,其安全指标采用超高顺坡率i0来衡量。按现有的齿轨车辆参数,计算得i0不大于4.6‰。考虑必要的安全系数[5],i0在一般条件下不超过2.0‰,在困难条件下可取2.5‰。
2.3.2.2 舒适度指标
齿轨铁路缓和曲线的舒适度指标包括超高时变率f和未被平衡横向加速度的时变率b。其中:f的取值应不致使引起乘客不适,需实测确定;b应根据工程条件难易度进行取值。
参考表2国内相关规范f和b的取值,因齿轨铁路速度较低,一般条件时f取35.0 mm/s,困难条件时f取40.0 mm/s。考虑到张家界七星山观光火车项目的选线灵活性,b在一般条件时取45.0 mm/s,在困难条件时取52.5 mm/s。
2.3.2.3 缓和曲线长度l0
l0应综合满足上述条件并取最大值,其计算式为:
l0=max{l01,l02,l03}
(6)
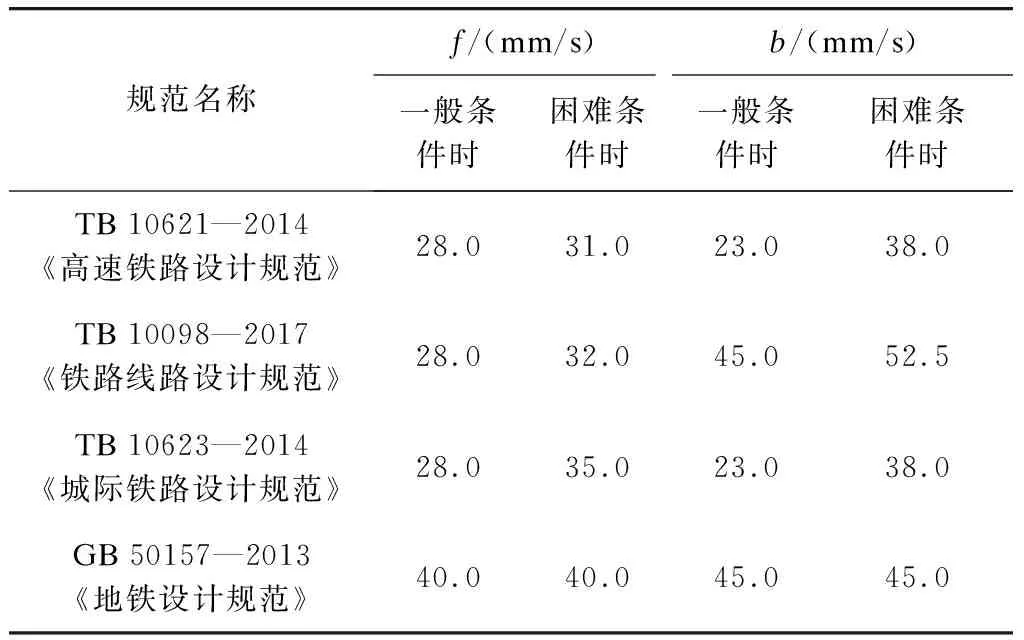
表2 国内相关规范中f和b取值
式中:
l01——满足车辆安全性要求的缓和曲线长度,l01=h/i0;
l02——满足超高时变率条件的缓和曲线长度,l02=hvmax/(3.6f);
l03——满足欠超高时变率条件的缓和曲线长度,l03=hqvmax/(3.6b)。
齿轨铁路vmax取30 km/h,h取最大值85 mm。根据式(6)及相关参数计算得到其缓和曲线长度的建议值,如表3所示。
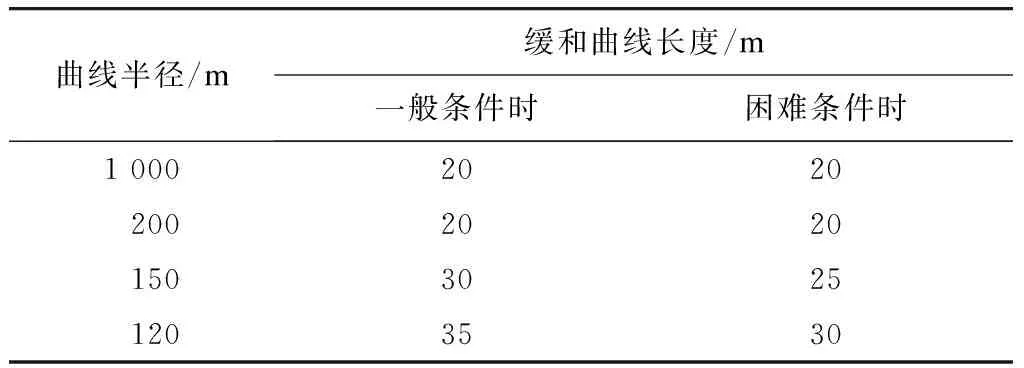
表3 齿轨铁路的线路缓和曲线长度建议值
2.4 夹直线和圆曲线最小长度
为避免1节车辆同时跨越在直线、缓和曲线和圆曲线3种线型上,造成车辆运动轨迹过渡不顺畅,影响运行安全,齿轨铁路的线路夹直线和圆曲线的最小长度拟定为不小于1节车的长度,即不小于20 m。
2.5 线间距
参照城市轨道交通线路的相关计算方法,齿轨铁路的的线路限界校核按列车速度35 km/h计算,供电方式采用接触轨下部授流,接触轨间距不小于500 mm,曲线段设备限界的横向加宽量及竖向加宽量分别取20 mm与25 mm。由此计算得到直线段的最小线间距为3.6 m,曲线段需加宽至3.7 m。因齿轨铁路多用于山区,曲线较多,正线线间距暂统一为3.7 m。
3 齿轨铁路线路纵断面设计参数研究
3.1 最大坡度
3.1.1 列车功率确定的最大坡度imax
imax主要取决于齿轨列车的功率、牵引性能和制动性能,其计算式为:
imax=(3 600pk-w0gvmax)/(gvmax)
(7)
式中:
imax——齿轨铁路的最大坡度,‰;
pk——牵引每吨列车所需功率,kW/t;
w0——列车以最高速度运行时受到的单位基本阻力,N/kN。
拟定齿轨车辆以设计最高速度30 km/h恒功运行,pk为22.5 kW/t。因齿轮提供的牵引力远大于齿轮转动的阻力,可忽略齿轮阻力,w0为3.674 N/kN。由式(7)得,imax为271.8‰。
3.1.2 安全条件所限制的最大坡度
3.1.2.1 工况一
工况一为齿轨车辆损失一半动力,可利用剩余动力在最大坡度条件下运行至指定地点,以0.5 m/s2作为判定车辆在最大坡道上能够启动的最小加速度,即:
(Fq-Wq-Wi1)/m≥0.5
(8)
Wi1=mgwi1/1 000
(9)
式中:
Fq——车辆启动牵引力,kN;
Wq——车辆起动基本阻力,kN;
Wi1——线路坡道附加阻力,kN;
wi1——车辆的单位坡道附加阻力,N/kN;
m——列车质量,t。
工况一下,齿轨车辆损失了一半牵引力,此时Fq为687 kN,m取168 t,单位起动基本阻力主要考虑粘着轮为8 N/kN,Wq为13 kN,由式(8)~(9)计算可得,wi1最大值358.3 N/kN。根据《列车牵引计算规程》规定,wi1可用坡道坡度千分数表示,数值相等,则该工况下坡道坡度的最大值为358.3‰。
3.1.2.2 工况二
工况二为齿轨车辆完全丧失动力时可通过齿轨工程车救援,需满足齿轨车辆最大坡道制动平均减速度不小于1.2 m/s2,即:
(B+Wo-Wi2)/mi2≥1.2
(10)
Wi2=mi2gwi2/1 000
(11)
式中:
mi2——工况二下联挂列车质量,t;
B——车辆制动力,kN;
Wo——车辆制动基本阻力,kN;
Wi2——线路坡道加速力,kN;
wi2——车辆的单位坡道加速力,N/kN。
工况二下,列车质量需增加救援工程车质量,故mi2=2m,即mi2取336 t。此时B为1 342 kN,Wo为12 kN,由式(10)、(11)计算可得,wi2的最大值为288.8 N/kN,则该工况下坡道坡度的最大值为288.8‰。
综上,齿轨铁路的最大坡度不应超过271.8‰。因齿轨列车的停放制动需要满足AW1(列车满员)工况下250‰坡道上安全、可靠地停放,并为给后续设计预留空间,齿轨铁路的最大坡度在一般条件时取235‰,困难条件时取250‰。如遇桥梁路段,需考虑到结构受力及安全施工条件进行单独计算。
3.2 竖曲线
3.2.1 线型选择
因圆弧形竖曲线测设、养护方便,齿轨铁路的竖曲线线型采用圆曲线形竖曲线。
3.2.2 竖曲线半径
3.2.2.1 安全条件下的竖曲线半径
齿轨列车在凸形竖曲线上运行时,因竖向离心力引起的车辆制动纵向压力及向上分力合力的减载作用可用减载率q表示,其计算式为:
(12)
式中:
RSH1——满足安全的竖曲线半径,m;
l——车辆钩舌距,m;
S——制动纵向压力,N。
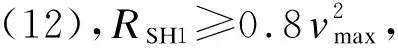
3.2.2.2 舒适度条件下的竖曲线半径
舒适度标准以竖向加速度为评价标准,满足舒适度条件的RSH2计算式为:
(13)
式中:
a——竖向离心加速度,m/s2;
国内外轨道交通线路中[6],a在一般条件时取0.07~0.30 m/s2。综合齿轨线路的特点,a在一般条件时取0.20 m/s2,困难条件时取0.40 m/s2,vmax取30 km/h。根据式(13)计算取整,RSH2在一般条件时取400 m,在困难条件时取200 m。
结合运行安全和舒适性条件,齿轨铁路最小竖曲线半径在一般条件时取400 m,在困难条件时取200 m。
3.2.2.3 最大竖曲线半径
比对国内轮轨交通的相关要求,齿轨铁路的最大竖曲线半径不宜大于4 000 m。
3.2.3 竖曲线设置的坡度差
齿轨列车的质量较小,且采用密接式车钩,相邻坡段的坡度差不受限制,故齿轨线路竖曲线的坡度差可参照GB 50157—2013《地铁设计规范》规定设置。
3.3 相邻竖曲线间的夹直线长度
夹直线长度需保证齿轨车辆在竖曲线路段的振动衰减完全。经初步研究,不同速度下车体在竖曲线起点处的振动衰减距离约为7~11 m,因此相邻竖曲线间最小夹直线长度暂推荐为15 m。
3.4 最小坡段长度lmin
lmin应结合竖曲线半径和相邻坡段最大坡度差计算,其计算式为:
lmin=2RSHΔimax/2 000+0.4vmax
(14)
式中:
RSH——竖曲线半径,m;
Δimax——相邻坡段最大坡度差,‰。
齿轨列车按3节编组考虑,车辆两端预留15 m,由式(14)可得lmin为100 m。
4 结语
本文从静态计算的角度出发,参考国内轮轨铁路平纵断面参数计算理论及实际运行经验,以张家界七星山观光火车项目为案例,研究了齿轨铁路的线路平纵断面主要技术参数,初步分析了齿轨铁路的线路曲线半径、缓和曲线、线间距、最大坡度及竖曲线设置、坡段长度的限制条件,并给出了相应的取值范围。本文的研究成果可以在工程设计中作参考运用。

