跳跃扩散过程下企业的最优投资策略

刘彦云， 胡支军**

(贵州大学 数学与统计学院， 贵阳 550025)

0 引 言

企业在投资一个新项目时，投资决策的不可逆性、项目收益的不确定性、投资时机的不确定性以及三者之间相互作用影响了企业的最佳投资时机，进而影响到投资项目的成败及项目收益的高低。对于企业来说，选择最佳投资时机的重点在于准确地衡量现实世界中的不确定性，并对其进行科学地刻画。传统的净现值投资决策方法不能适当地处理风险项目中的不确定因素，也没有考虑资本的不可逆性以及项目灵活性的战略意义；实物期权方法突破了传统方法将不确定性视为风险的局限性，把不确定性价值包含在投资项目的价值中。因此，自Myers(1977)[1]首次提出利用实物期权方法来描述投资机会价值之后，这一方法迅速被该领域的众多学者广泛采用。

实物期权的观点是将企业所拥有的投资机会视为一个看涨期权，执行这一看涨期权的代价不仅包括投资时需要支付的投资成本，还包括由此丧失的投资机会。从实物期权的观点出发，企业最佳投资时机的选择问题即可转化为投资期权的定价问题。McDonald和Siegel(1986)[2]首次将实物期权方法运用于研究不可逆投资计划的最佳投资时机，讨论了投资期权的定价问题，并推导出最佳投资时机的决定方法。运用实物期权方法研究企业投资问题的大多数文献是从单个因素的不确定性出发，对于多个不确定因素以及不确定性之间具有相关性的研究相对较少。

Dixit & Pindyck(1994)[3]考察了项目的运营成本和产出价格均不确定时企业的投资决策；Murto[4]考察了项目投资成本和未来收益不确定时企业的最佳投资策略；Pennings & Sereno[5]考察了制药企业的研发项目在技术和经济环境不确定性下的项目价值问题;Nunes & Pimentel[6]考察了一个成熟企业面临新项目的投资成本和产出需求不确定时的最优投资决策问题。以上学者研究的共同点是假设企业同时面临两种不同来源的不确定性，且不确定因素之间相互独立。在实际的经济环境中，风险之间相关影响是很常见的现象。

现有文献大多都假设不确定因素的变化路径是连续的，并运用几何布朗运动对其进行模拟。Yang & Liu[7]在假设市场需求与投资成本不确定且两者的随机波动彼此相关的条件下，假设两种不确定因素的变化路径服从几何布朗运动，利用期权博弈方法，建立了先占和非先占情况下的双寡头期权博弈模型，得出了企业在各博弈模型中的价值函数和投资临界值，分析了相关参数对企业最优投资决策的影响；Moawia & Alghalith[8]在假设产出价格和市场需求不确定的条件下建立了竞争企业在多重相关不确定性下的动态连续时间模型，但没有考虑不确定因素受到突发事件冲击的情形。然而，越来越多的证据显示，不确定因素的变化路径并不总是连续的，尤其是受到一些突发事件的影响时，往往会发生跳跃进而出现一些不连续点。从资产组合风险管理问题到期权债权的定价问题，现有文献如Merton[9]，Pan[10]，Liu & Longstaff[11]，Johannes[12]，Lee & Mykland[13]，Yang & Chen[14]，Hagspiel & Huisman[15]等，都证实了突发事件的存在以及对企业投资决策的影响。因此，在研究企业的最优投资策略时，选用合适的模型对突发事件进行模拟尤为重要。Eberlein[16]指出，可以将金融领域的一些先进模型引入跳跃过程来模拟这种由突发事件所导致的跳跃，以期真实准确地描绘不确定因素的变化路径，得到企业的最优投资策略；Yang & Chen[14]在假定跳跃幅度随机但不依赖于具体分布形式的框架下，运用数值分析方法分析了跳跃幅度的3个统计特征参数对企业投资策略的影响；Nunes & Rita Pimentel[6]假定产品需求和成本服从跳跃扩散过程，只考察了突发事件到达强度和平均跳跃幅度对投资阈值的影响。

综上所述，现有文献有如下局限性：第一，考虑了多重不确定因素但没考虑不确定因素波动率之间的相关性；第二，忽略了突发事件对不确定因素的影响；第三，考虑了突发事件的存在，但没能全面分析突发事件对企业投资策略的影响。针对现有文献的这些局限性，本文从以下几个方面进行了突破。首先，考虑了不确定因素的随机波动具有相关性的情形。在Nunes & Pimentel[14]的基础上，放松了投资成本和产出价格的随机波动相互独立的假设；其次，考虑了突发事件对两种不确定因素的影响，在Yang和Chen[12]的基础上，给出了平均跳跃幅度、跃度波动率、跃度偏度值这3个统计特征参数对企业投资策略影响的理论证明，并运用数值模拟方法验证了理论证明结果，进而推广了比较静态结果。

1 模型及求解

这一部分，首先给出项目的投资成本和产出价格所服从的随机过程——跳跃扩散过程，其次建立投资期权的定价模型，最后求解模型。

1.1 动态过程

假设企业投资前面临两种不同来源的不确定因素：投资成本和产出价格，分别记为I，P。它们的变化路径几乎处处连续，间断点是受突发事件的影响而产生的跳跃。基于其变化路径的特点，本文运用跳跃扩散过程对其进行模拟。

跳跃扩散过程表示不确定因素的变化动态由两种不同类型构成：一种是正常的波动，其路径是连续变化的，用几何布朗运动来模拟；一种是非正常的波动，由突发事件引起的一些跳跃构成，用跳跃过程来模拟。

突发事件到达的次数是随机的，记为{Nt，t≥0}，假设其服从强度为λ的泊松分布。突发事件引起的跳跃幅度{Ui}i∈N也是随机的，假设其独立同分布于随机变量U，即{Ui}i∈Ni.i.d～U，i.e。假设随机变量U的概率密度函数为φ(u)。

记Y={Yt：t≥0}是一个跳跃扩散过程，其微分形式表示如下：

(1)

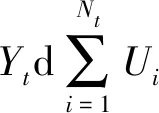
项目的投资成本和产出价格所服从的跳跃扩散过程分别表示如下：

(2)

(3)

假设投资成本和产出价格的随机波动之间具有相关性，记为

E(dWtPdWtI)=ρdt

(4)

其中：ρ表示相关性系数，上标和下标中的I，P分别为相应的投资成本和产出价格参数。

1.2 项目价值

投资前，企业只持有一个投资期权。在时刻τ，企业以一次性支付投资成本Iτ的方式执行了该期权，同时拥有了一个价值为V(P，I)的项目，则企业的项目价值满足如下方程：

(5)

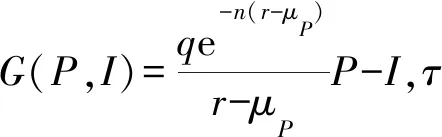
在时间[t，t+dt]内，项目价值V(P，I)满足的HJB方程rVdt=E(dV)，由伊藤引理可得：

F(P，I)]φ2(uI)duI=0

(6)

1.3 模型求解

式(6)是含有两个状态变量的偏微分方程，参考Dixit & Pindyck[3]以及Nunes & Pimentel[6]中求解同时考虑两种不确定因素的投资问题的方法，将二维的投资问题简化至一维并求解。

(7)

其中,f为待定函数。

G(P，I)=Il(θ)

(8)

其中：

(9)

HJB方程式(6)可用新变量重新表示为

(10)

如果不考虑投资成本和产出价格之间随机波动相关的情况，则方程式(10)可以简化为

(11)

命题1 HJB方程式(10)的解f(θ)具有如下形式：

(12)

其中：

(13)

β1是HJB方程的基本二次型J(β)的大于1的根，J(β)具体表达式如下：

(14)

在Nunes & Pimentel(2017)[6]模型的基础上考虑了相关性，如果不考虑投资成本和产出价格在几何布朗运动部分的随机波动相关性，则上述基本二次型可简化为

(15)

考虑了随机波动相关性之后，方程式(14)的根β1与相关性系数ρ有关，而方程式(15)的根与ρ无关。

2 比较静态分析

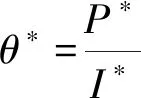
接下来，先给出相关参数对投资阈值影响的理论推导过程和结果，再给出具体的数值模拟以验证理论证明结果。通过固定其他参数值，让目标参数在一定的区间范围内变化进而模拟投资阈值的变化趋势。在参数设定上，当考察几何布朗运动参数对投资阈值的影响时，将跳跃过程的参数均设定为0。对于几何布朗运动部分参数，参考Dixit & Pindyck[3]对无风险利率r，投资成本和产出价格期望增长率μp，μI，波动率σp，σI，ρ的设定，以及Nunes & Pimentel(2017)[6]关于产量q，项目建造时间n的设定；跳跃参数设定参考Yang & Chen[12]。下面先给出一个后面的证明需要用到的引理。

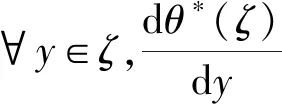
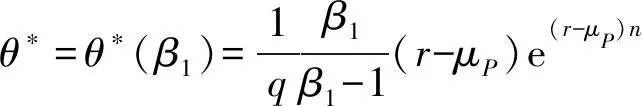
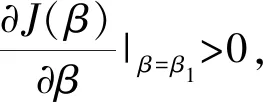
因此，投资阈值θ*关于最相关参数的变化行为依赖于投资问题的HJB方程对应的基本二次型J(β)关于对应的最相关参数的变化行为。换言之，要考察投资阈值关于最相关参数的变化行为，只需要考察基本二次型J(β)与对应的最相关参数的变化行为即可。

2.1 随机波动率及相关性参数对投资阈值的影响分析

相关性系数是表示两个变量之间相关关系密切程度的统计分析指标。下面给出投资成本和产出价格的随机波动相关性系数ρ的实际意义：

(1)ρ>0，投资成本和产出价格的随机波动呈现正相关，表示当投资成本的随机波动率增大时，产出价格的随机波动率也随之增大。

(2)ρ<0，投资成本和产出价格的随机波动呈现负相关，表示当投资成本的随机波动率增大时，产出价格的随机波动率随之减小。

(3)ρ=0，投资成本和产出价格的随机波动之间不存在线性关系，此时模型简化为Nunes & Pimentel[6]所用模型。

(4)ρ=1，投资成本和产出价格的随机波动之间完全正相关，表示当投资成本的随机波动率增大(减小)时，产出价格的随机波动率也随之以一定的比例增大(减小)。

(5)ρ=-1，投资成本和产出价格的随机波动之间完全负相关，表示当投资成本的随机波动率增大(减小)时，产出价格的随机波动率随之以一定的比例减小(增大)。

下面的命题给出投资成本和产出价格的随机波动相关性参数对投资阈值的影响。

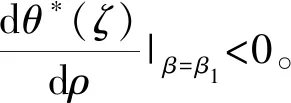
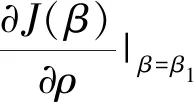
-σPσIβ1(β1-1)<0

故得证。

其他参数设置为μI=0.01，μp=0.02，σI=0.01，σp=0.02。

从图1来看，无论投资成本和产出价格的随机波动率呈正相关还是负相关，相关性越大，投资阈值越小，企业通过加快执行投资策略的方式来应对不确定因素的随机波动率之间具有的相关性情形。与命题2的证明结果一致。

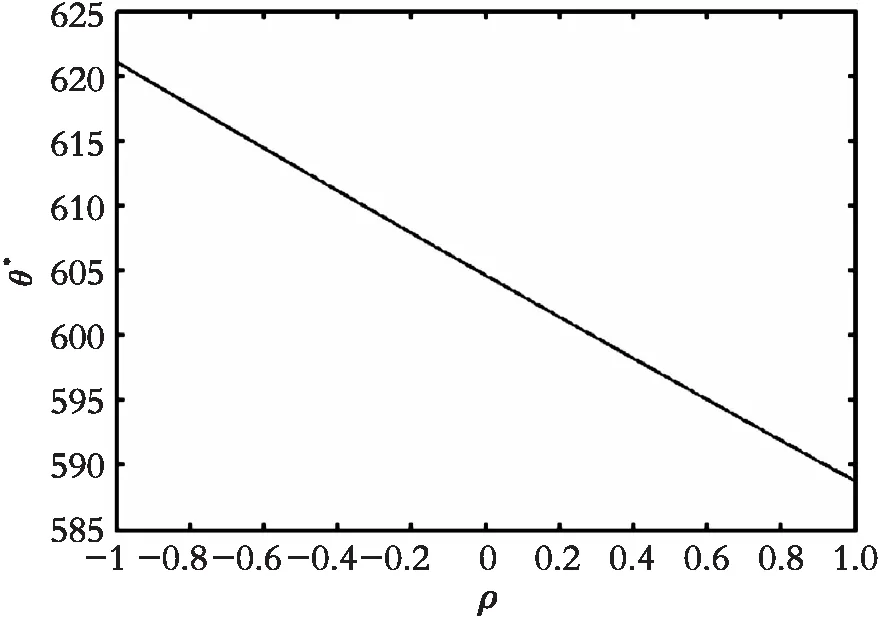
图1 投资阈值θ*关于相关性ρ的变化趋势Fig. 1 The change trend of investment threshold θ* with respect to correlation ρ

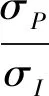
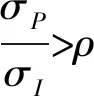
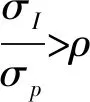
特别地，当σP<σI时，θ*关于σP单调递减；当σP>σI时，θ*关于σI单调递减。

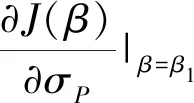
结论显然。

图2中：μI=0.01，μp=0.02，σI=0.01，ρ=-0.5；图3中：μI=0.01，μp=0.02，σP=0.02，ρ=-0.5。

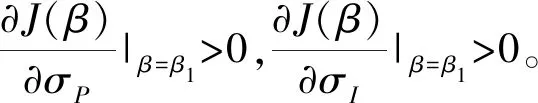
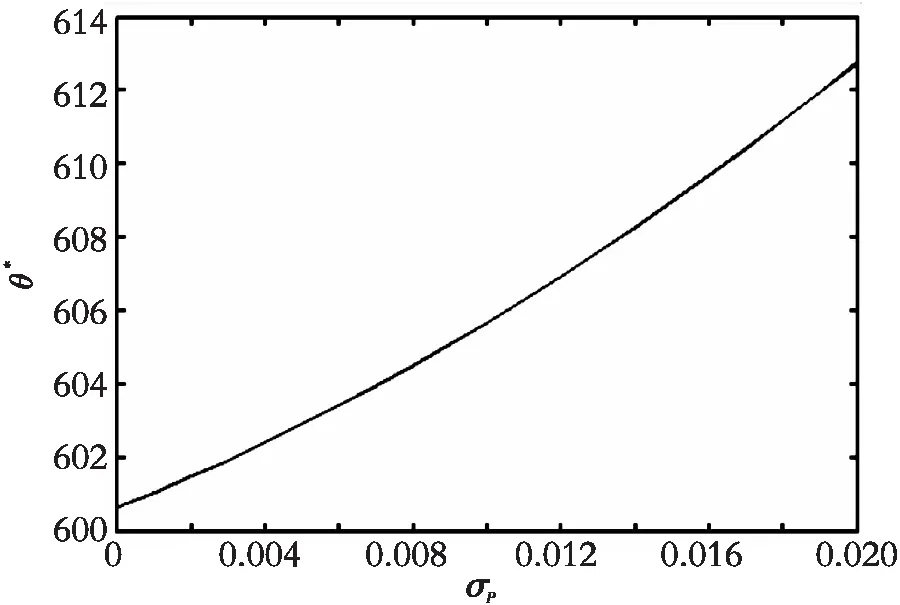
图2 产出价格波动率对投资阈值的影响(ρ<0)Fig. 2 The influence of output volatility on investment thresholod (ρ<0)

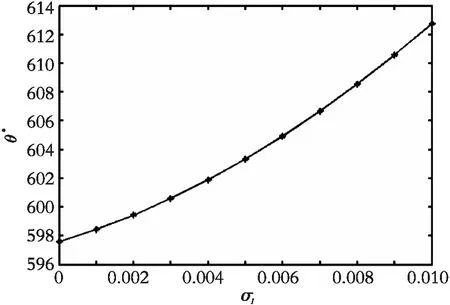
图3 投资成本波动率对投资阈值的影响(ρ<0)Fig. 3 The influence of investment cost volatility on investment threshold (ρ<0)

图4中：μI=0.01，μp=0.02，σI=0.01，ρ=0.5；图5中：μI=0.01，μp=0.02，σP=0.02，ρ=0.5。

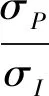
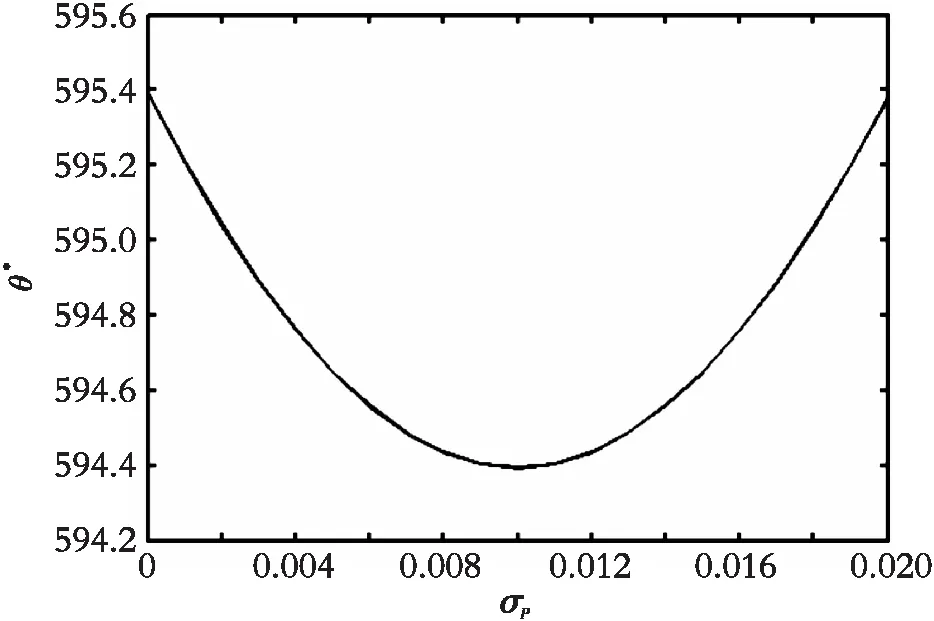
图4 产出价格波动率对投资阈值的影响(0<ρ<1)Fig. 4 The influence of output price volatility on investment threshold (0<ρ<1)

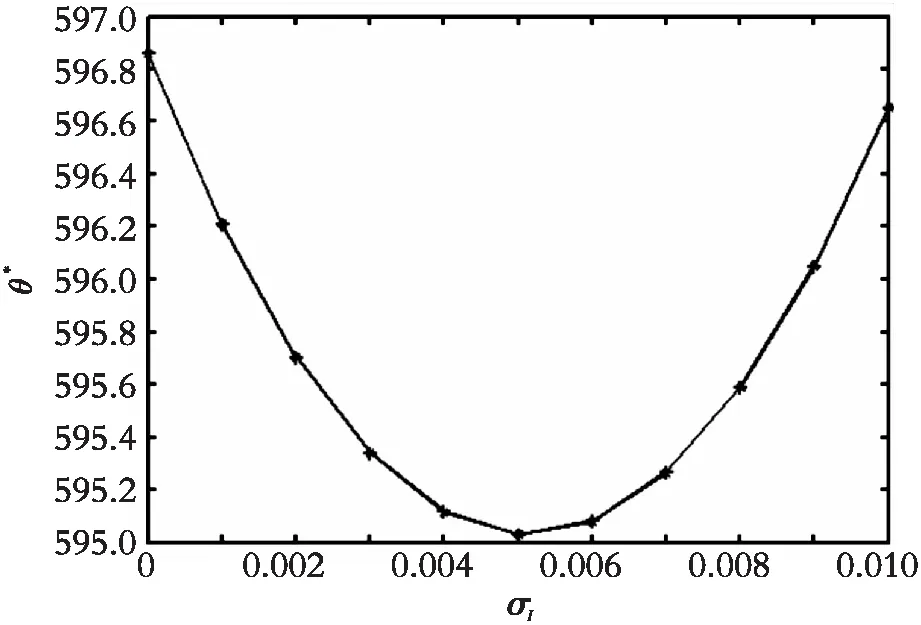
图5 投资成本波动率对投资阈值的影响(0<ρ<1)Fig. 5 The influence of investment cost volatility on investment threshold (0<ρ<1)

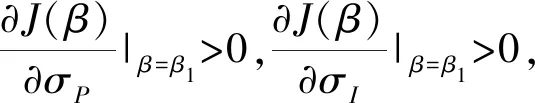
这一结论是本文开创性的成果：Nunes & Pimentel[6]在假设需求和投资成本相互独立的框架下发现投资阈值关于二者的随机波动率均单调递增。本文放松了投资成本和产出价格两种不确定因素的随机波动相互独立的假设，考虑了彼此相关的情形。研究结果表明：随机波动率对投资阈值的影响不仅与自身有关，还要取决于相对波动率和相关性系数之间的关系。

2.2 突发事件对投资阈值的影响分析

为了更加全面地考察突发事件的影响，本文在Nunes & Pimentel[6]仅考察突发事件到达强度和平均跳跃幅度对投资阈值影响的基础上，参考Yang & Chen[12]所用的方法，运用跳跃幅度的3个统计特征参数：均值、标准差、偏度来考察突发事件对两种不确定因素下企业投资阈值的影响。

这3个统计特征参数直观的经济意义如下：

(1) 跳跃幅度的均值m=(mp，mI)，表示突发事件对投资成本和产出价格的平均作用强度；

(2) 跳跃幅度的标准差δ=(δp，δI)，表示突发事件对投资成本和产出价格作用强度的波动率；

(3) 跳跃幅度的偏度Skew=(Skewp，SkewI)，代表突发事件对投资成本和产出价格作用的方向。Skewp>0代表突发事件有较大可能性将引起产出价格的异常上升；Skewp<0则代表突发事件有较大可能性将引起产出价格的异常下跌。本文假设Skew∈(-0.8，0.8)，根据Gauss-Statistics求积原理，采用两节点近似方法后，J(β)中的积分项可分别表示为

w1P(1+x1)β1+w2P(1+x2)β1

w1I(1+y1)1-β1+w2I(1+y2)1-β1

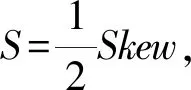
基本二次型式(14)可重新表示为

(λP+λI)-r)+λPw1P(1+x1)β1+w2P(1+x2)β1+

λIw1I(1+y1)1-β1+w2I(1+y2)1-β1

至此，基本二次型式(14)中的积分项已经不再依赖于φ1(up)，φ2(uI)的具体形式，而仅取决于3个统计特征参数：均值m=(mp，mI)，标准差δ=(δp，δI)，偏度Skew=(Skewp，SkewI)。

下面给出突发事件具体的比较静态分析结果。

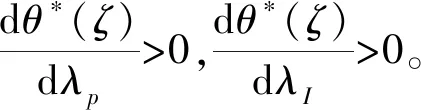
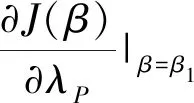
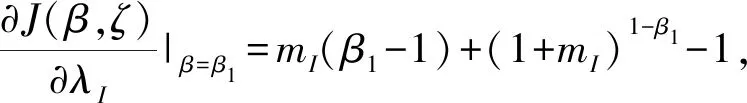
图6中：μI=0.01，μp=0.02，σI=0.01，σP=0.02，mP=0.5，δP=0.2，SP=0，ρ=0.5；图7中：μI=0.01，μp=0.02，σI=0.01，σP=0.02，mI=0.5，δI=0.2，SI=0，ρ=0.5。

由图6和图7可知，无论突发事件性质如何，跳跃到达强度越大，投资阈值越大，企业的最佳策略为延迟执行投资期权，与命题4 的结论一致。

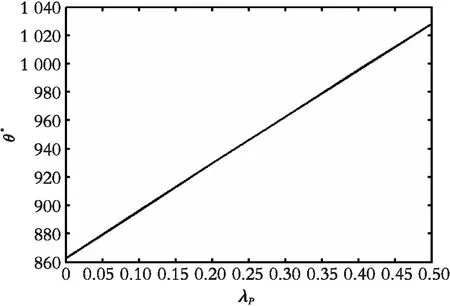
图6 产出价格突发事件到达强度对投资阈值的影响Fig. 6 The influence of the arrival intensity of output price’s shocks λp on investment threshold θ*

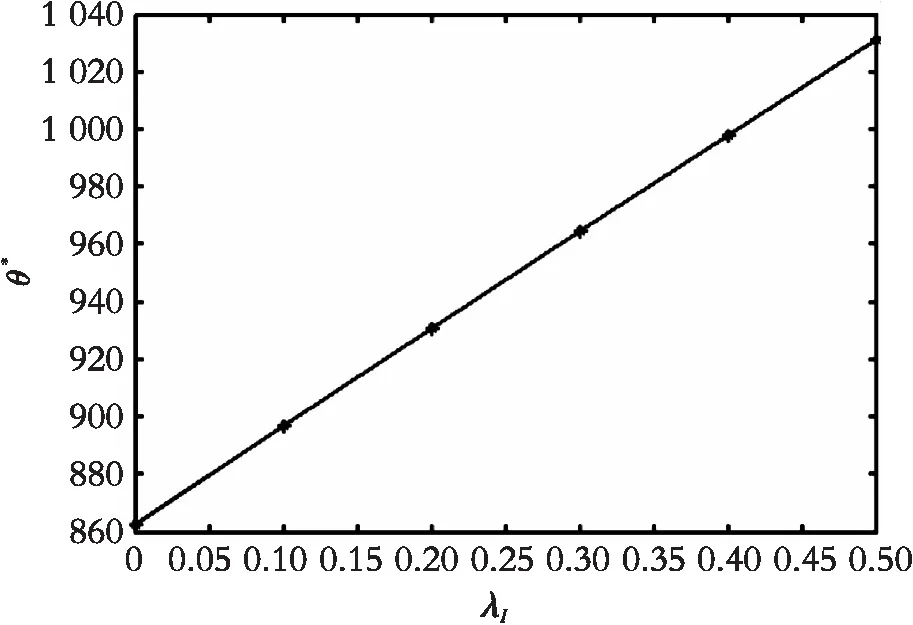
图7 投资成本突发事件到达强度对投资阈值的影响Fig. 7 The influence of the arrival intensity of investment cost’s shocks λI on investment threshold θ*

命题5 投资阈值θ*关于突发事件平均跃度m=(|mP|，mI)单调递增。

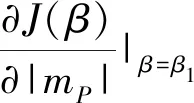
首先考察产出价格突发事件对投资阈值的影响。

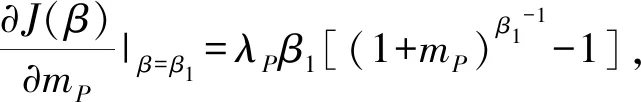
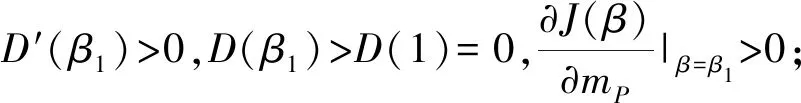
其次，考察投资成本突发事件对投资阈值的影响。

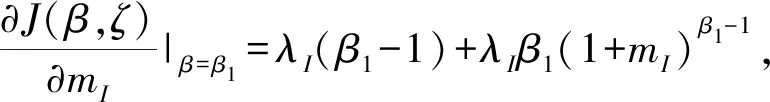
命题6 投资阈值θ*关于产出价格跳跃幅度波动率δP单调递增，关于投资成本跳跃幅度波动率δI单调递减。

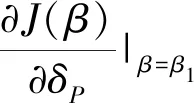
首先证明投资阈值θ*关于产出价格跳跃幅度波动率δP单调递增。

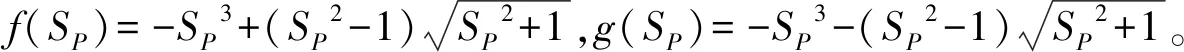
其次，证明投资阈值θ*关于投资成本跳跃幅度波动率δI单调递减。

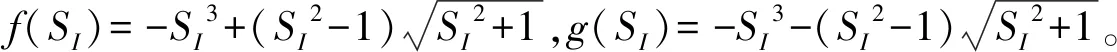
命题7 投资阈值θ*关于产出价格跳跃幅度偏度Skew(Up)单调递减，关于投资成本跳跃幅度偏度Skew(UI)单调递增。

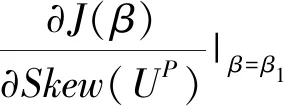
首先，考察投资阈值θ*与产出价格跳跃偏度Skew(UP)之间的关系。

其中：

Ψ(SP)=β1δP(f(SP)(1+x1)β1-1+g(SP)(1+x2)β1-1)

其次考察投资阈值θ*与投资成本跳跃幅度偏度Skew(UI)之间的关系：

其中：

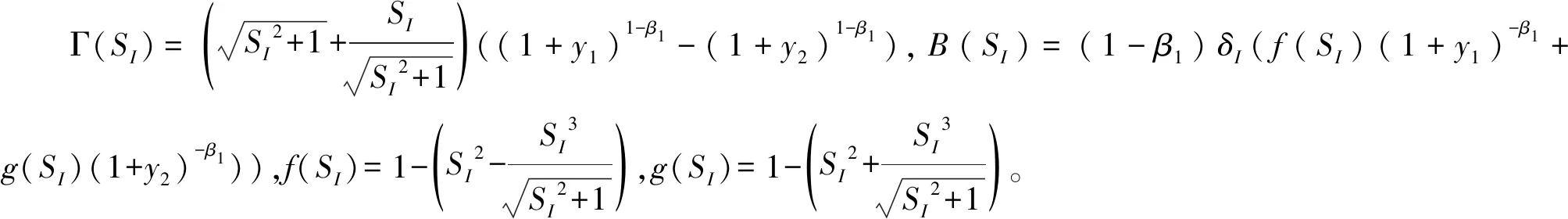
在结果分析之前，先给出“无偏倚”事件的定义，即跳跃幅度均值和偏度均为0。从长期来看， 其影响并不足以导致投资阈值发生趋势性变化(即均值为0)，而且，好事件和坏事件发生的概率平均来看总是相等的(即偏度为0)。

在考察突发事件跳跃幅度对投资阈值的影响时，从一个”无偏倚”的突发事件出发，然后逐步扭曲突发事件的”无偏倚性”，让跳跃幅度均值在[-0.5， 0.5]内变化，跳跃幅度偏度[-0.4， 0.4]内变化，并在4个标准差区间0.1，0.2，0.3，0.4内考察投资阈值关于跳跃幅度的变化趋势。图5为投资阈值θ*关于产出价格跳跃幅度均值、标准差、偏度的变化趋势。

其他参数设置：μI=0.01，μp=0.02，σI=0.01，σP=0.02，ρ=0.5。

从图8来看，无论产出价格跳跃幅度标准差取哪个值，投资阈值关于产出价格跳跃幅度均值和偏度的变化趋势都一致，且投资阈值均关于平均跳跃幅度绝对值单调递增，当固定平均跳跃幅度时，投资阈值关于跳跃幅度偏度单调递减。由此可见，引起投资阈值波动的主要因素是产出价格跳跃幅度均值和偏度而不是标准差，这就意味着在考察产出价格突发事件的影响时， 企业应重点考察突发事件的平均作用强度和突发事件的影响方向，即预测即将来临的突发事件是利好消息还是利空消息。而且，投资阈值关于产出价格跳跃偏度单调递减，也就是说，当产出价格的突发事件的利好性质越明显， 企业越应加快执行投资期权。同样地，该方法可以分析投资成本突发事件对投资阈值的影响，此处不做赘述。

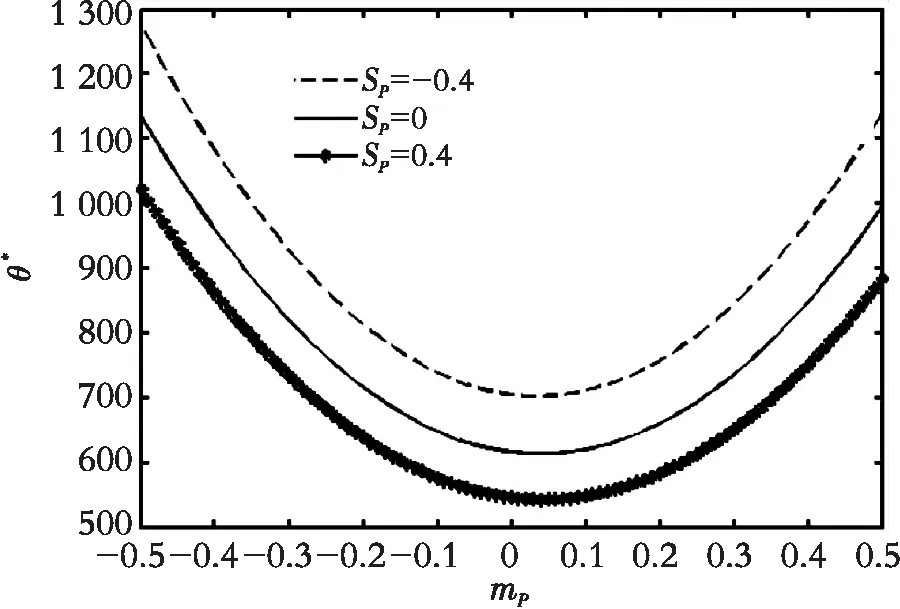
(a) δP=0.1

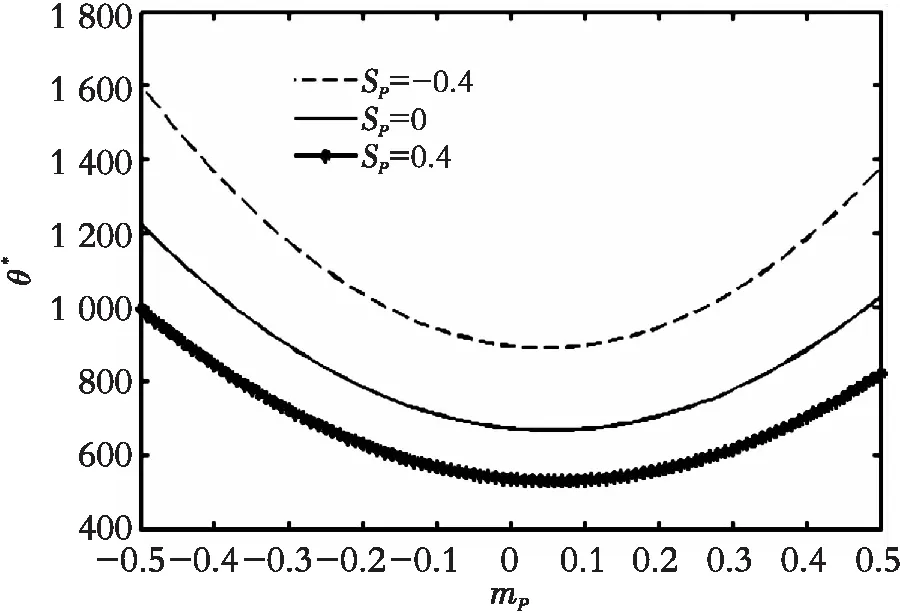
(b) δP=0.2

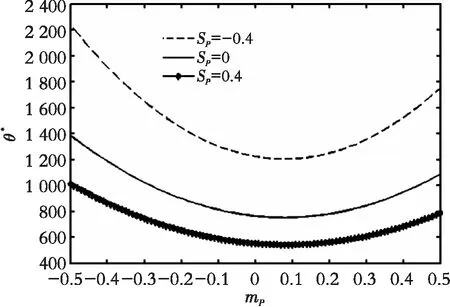
(c) δP=0.3

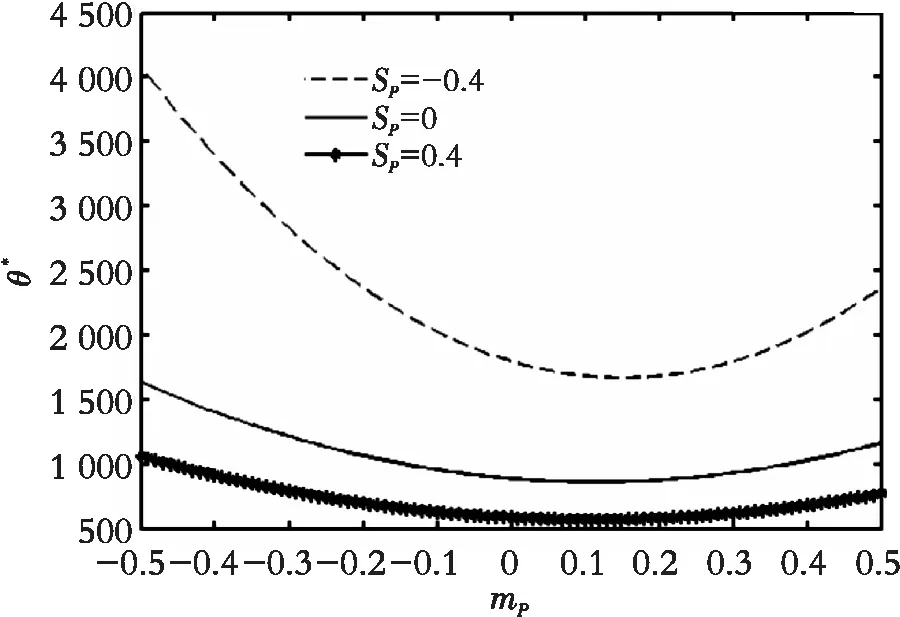
(d) δP=0.4

3 结 论

本文假设企业投资前面临两种不确定因素：项目的投资成本和产出价格。通过放松两种不确定因素相互独立的假设，考虑了投资成本和产出价格的随机波动之间具有相关性的情形；同时考虑了突发事件对两种不确定因素的影响，在保留跳跃幅度随机分布的假设框架下，运用3个统计特征参数：平均跳跃幅度、跃度波动率、跃度偏度对突发事件进行刻画，并结合理论证明和数值分析研究了突发事件对投资阈值的影响，进而推广了比较静态结果。

结果表明：投资成本和产出价格之间波动相关性越大，企业的投资阈值越小，此时企业的最佳策略为加快执行投资期权。同时发现：投资成本和产出价格的突发事件到达强度及平均跳跃幅度对投资阈值的影响一致，到达强度越大，投资阈值越大；同样地，平均跳跃幅度越大，投资阈值越大，此时企业的最优策略为延迟执行投资期权。而投资成本和产出价格的跳跃幅度波动率和偏度对投资阈值的影响恰好相反，产出价格的跳跃幅度波动率越大，投资阈值越大，跳跃幅度偏度越大，投资阈值越小；而投资成本的跳跃幅度波动率越大，投资阈值越小，跳跃幅度偏度越大，投资阈值越大。这一结果与现实情况符合。同时，在综合分析跳跃幅度均值、波动率、偏度对投资阈值共同的影响时发现：引起投资阈值波动的主要因素是跳跃幅度均值和偏度而不是标准差，因此企业在作出投资策略前应重点考察突发事件的性质和影响方向。

参考文献(References):

[1] MYERS S C. Determinants of Corporate Borrowing[J]. Journal of Financial Economics，1997(5)：147—195

[2] MCDONALD R， SIEGEL D. The Value of Waiting to Invest[J]. The Quarterly Journal of Economics， 1986,101(4):707—727

[3] DIXIT A K， PINDYCK R S. Investment under Uncertainty[J]. Economics Books， 1994， 39(5)：659—681

[4] MURTO P. Timing of Investment under Technological and Revenue-related Uncertainties[J]. Journal of Economic Dynamics and Control， 2007， 31(5):1473—1497

[5] PENNINGS E， SERENO L. Evaluating Pharmaceutical R&D under Technical and Economic Uncertainty[J]. European Journal of Operational Research， 2011， 212(2)：374—385

[6] NUNES C， PIMENTEL R. Analytical Solution for an Investment Problem under Uncertainties with Shocks[J]. European Journal of Operational Research，2017，259(3)：1054—1063

[7] 杨巧曼， 刘亚相. 市场需求与投资成本不确定条件下的双寡头期权博弈模型[J]. 系统工程，2018，36(4)：158—162

YANG Q M， LIU Y X. Duopoly Option Game Model of Uncertain Market Demand and Investment Cost[J].Systems Engineering，2018，36(4)：158—162(in Chinese)

[8] ALGHALITH， MOAWIA. Theory of the Firm under Multiple Uncertainties[J]. Mpra Paper， 2016， 251(1)：341—343

[9] MERTON R C . Option Pricing When Underlying Stock Returns are Discontinuous[J]. Journal of Financial Economics， 1976， 3(1)：125—144

[10] PAN J. The Jump-risk Premia Implicit in Options：Evidence from an Integrated Time-series Study[J]. Journal of Financial Economics， 2002， 63(1)：3—50

[11] LIU J， LONGSTAFF F A， PAN J， et al. Dynamic Asset Allocation with Event Risk[J]. Journal of Finance， 2003， 58(1)：231—259

[12]JOHANNES M. The Statistical and Economic Role of Jumps in Continuous-Time Interest Rate Models[J]. Journal of Finance， 2004，59(1)：227—260

[13]LEE SS， MYKLAND P A. Jumps in Financial Markets：A New Nonparametric Test and Jump Dynamics[J]. Review of Financial Studies， 2008， 21(6)：2535—2563

[14]杨海生， 陈少凌. 不确定条件下的投资：基于”跳”过程的实物期权模型[J]. 系统工程理论与实践， 2009， 29(012)：175—185

YANG H S， CHEN S L. Investment under Uncertainty：A Real Option with Jump Process[J].Systems Engineering Theory & Practce， 2009， 29(12)：175—185(in Chinese)

[15]HAGSPIEL V， HUISMAN K J M， NUNESC， et al. Optimal Technology Adoption When the Arrival Rate of New Technologies Changes[J]. European Journal of Operational Research， 2015， 243(3)：897—911

[16]GLAU E. Variational Solutions of the Pricing PIDEs for European Options in Levy Models[J]. Applied Mathe-matical Finance, 2014,21(5):417—450

[17]PIMENTEL P，AZEVEDOPEREIRA J， COUTO G， et al. High Speed Rail Transport Valuation[J]. European Journal of Finance， 2012， 18(2)：167—183

[18]COUTO G， NUNES C， PIMENTEL P. High-speed Rail Transport Valuation and Conjecture Shocks[J]. European Journal of Finance， 2015， 21(10—12)：791—805

[19]HE L， LIANG Z. Applied Stochastic Control of Jump Diffusions[J]. Journal of Industrial & Management Optimization， 2007， 13(2)：11—11

[20]ØKSENDAL， BERNT， SULEM， et al. Applied Stochastic Control of Jump Diffusion[J]. Mathematical Methods of Operations Research, 2006,62(2):345—346

[21]WESTMAN J J， HANSON F B. Nonlinear State Dynamics：Computational Methods and Manufacturing Application[J]. International Journal of Control， 2000， 73(6)：464—480