一类随机互惠模型的遍历性和最优收获策略*

罗 俊 威

(南京财经大学 应用数学学院，南京 210023)

0 引 言

近年来，随着可持续发展战略被大力宣传与实施，更多的研究者也把注意力放在了自然资源的分配与使用中，例如天然气、化石燃料、金属以及生物资源都受到了重视。虽然部分资源本身具有可再生的能力，但是过度开采已经使得那些不可再生资源处于短缺甚至耗尽边缘， 而且很多动物在大肆的捕获下也濒临灭绝。因此，最优收获问题应运而生，如何控制收获力度保证可持续发展成为很多生物研究者的研究主题。

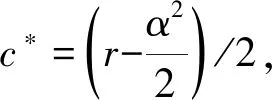
目前，大部分的研究(如文献[3，6，9，11])都是对典型的线性Lotka-Volterra模型进行一系列的研究，本文则主要考察May在文献[7]中提到的一类非线性互惠模型，其表达式如下：

(1)

其中：x(t)，y(t)代表两个物种在时刻t时的数量密度；ri(i=1，2)表示物种x(t)，y(t)的内在增长率；K1是在没有y(t)的影响下环境对x(t)的容纳量，K2反之；qi(i=1，2)表示分别对x(t)，y(t)的收获效力；bi表示互惠系数；εi表示种内竞争系数；ri，Ki，bi，εi都是正常数，并且f(·)，g(·)为单调连续递增的正函数；Wi(t)(i=1，2)是两个标准布朗运动，其中 {Ft}t≥0代表域流为一个σ-代数，αi2(i=1，2)代表着白噪声的强度。f，g的存在也让这个模型具有代表性，下面主要对其在白噪声扰动下的随机性质以及最优收获问题进行探讨。

(1)x(t)和y(t)都是持续存在的；

(2) 确定期望的可持续产出(ESY)：

有最优值或范围。

1 预备知识

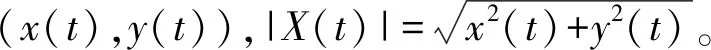
引理1[8-9]设φ(t)∈[Ω×[0，+∞)，R+]，

(1) 如果存在3个常数λ0，λ和T≥0，使得对所有的t≥T，有

其中α是常数， 于是

(2) 如果存在3个常数λ0，λ和T≥0， 使得对所有的t≥T， 有

于是

定义1 如果x(t)，y(t) 满足条件：

于是就说式(1)是平均持续的。

2 主要结论

系统正解的存在唯一性对后续性质的探讨起着至关重要的作用，接下来，先证明式(1)存在唯一全局正解。

定理1 对于给定的正初值(x0，y0)，式(1)有一个唯一全局正解(x(t)，y(t))。

证明令u(t)=lnx(t)，v(t)=lny(t)，对式(1)使用It公式，得到

(2)

其中:t≥0，初值u(0)=lnx0，v(0)=lny0，由于系数满足李普希茨条件，再利用文献[14]中随机微分方程的理论，可证式(1)在t∈[0，τ)上有唯一局部解，其中τ为爆破时间，因此(x(t)，y(t))有唯一局部解。对于全局解，即τ→+∞时，利用随机方程的比较原理，参考文献[10]中的方法，得证。

生物的持续与灭绝对维持自然界物种多样性起着至关重要的作用，物种生物量的多少也决定着人类如何实施最优收获策略。下面开始讨论生物持续生存的条件。

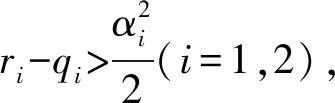
证明对式(1)的第一个等式使用It公式，可以得到

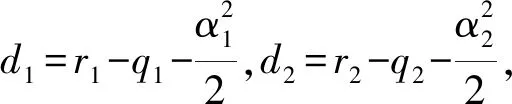
同样， 对y(t)，有

从而证明了系统平均持续性。

探讨最优收获策略不仅能帮助人类充分利用自然资源并获得最大收益，而且也能保证物种生物量维持在一个合理的水平，避免因过度开发而灭绝。在确定最优收获策略之前，先给出一个引理。

证明证明方法可参考文献[11]。

定理3 式(1)的测度μ(·)具有遍历性。

证明根据引理2，可知式(1)的不变测度μ(·)是唯一的。利用文献[12]中的推论3.4.3，可得μ(·)是强混合的。同样，基于文献[12]中的定理3.2.6，则μ(·)具有遍历性。

现在，开始确定式(1)的最优收获策略。

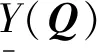
以及

证明令Q=(q1，q2)T>0，并且x(t)，y(t)是平均持续的，得到

(3)

通过引理2， 再利用文献[12]中的式(3.3.2)，有

(4)

设τ(X)表示式(1)的平稳概率密度，则

(5)

由于式(1)的不变测度具有唯一性，推出

(6)

结合式(3)—(6)得到最优收获的表达式：

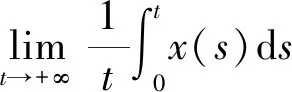
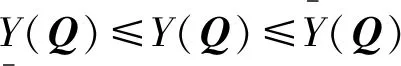
其中：

由于连续性，可以知道存在两个正常数

使得

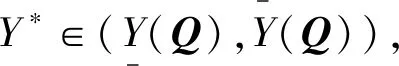
3 数值模拟

利用数值模拟的方法展示前面章节所得到的结果， 并观察在引入最优收获时， 生物持续和灭绝的情况。根据文献[13]中 Milstein的方法，确定一些常量r1=1，r2=1.2，ε1=0.7，ε2=0.8，b1=0.9，b2=0.7，K1=K2=2以及f(y)=ey，g(x)=ex，且初值为X(0)=(0.6，0.4)。

图1表示了在自然随机扰动条件下，生物的生长情况，其中α1=0.15，α2=0.18，q1=q2=0。图2模拟在和图1同等强度随机干扰的情况下，施加最优收获效力后生物的生长变化，即q1=0.494，q2=0.592，可以看到生物的数量明显下降了一个等级，但却仍能持续存在。并且通过对比图1，图2 的生物数量变化，可以发现x(t)的数量从平均值为1下降到平均值为0.5左右，大约下降了0.5，而y(t)则由1.1下降到了0.52，大致下降了0.58。这与通过上一部分计算出来的最优收获效力q1=0.494，q2=0.592的结论相一致，并且算得最优收获Y(Q)处于(0.52，0.71)之间。另外通过图1，图3的对比发现在扰动强度很大的情况下，即对于图3中α1=1.6，α2=1.8，物种大概率会灭绝，因此无法进行捕获，这也验证了之前得到的结论。

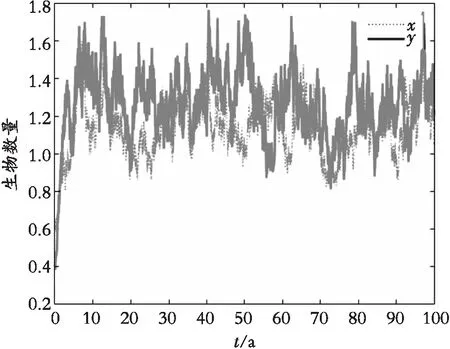
图1 随机扰动下无收获的生物数量图Fig. 1 Biological quantity diagram under stochastic disturbances with no harvesting

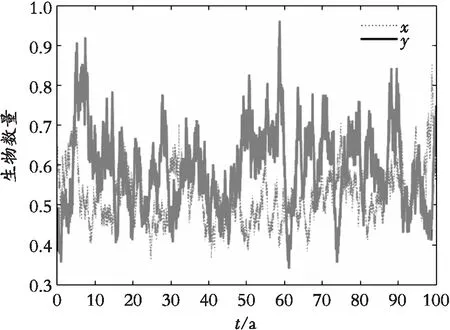
图2 随机扰动下施加收获的生物数量图Fig. 2 Biological quantity diagram under stochastic disturbances with optimal harvesting efforts

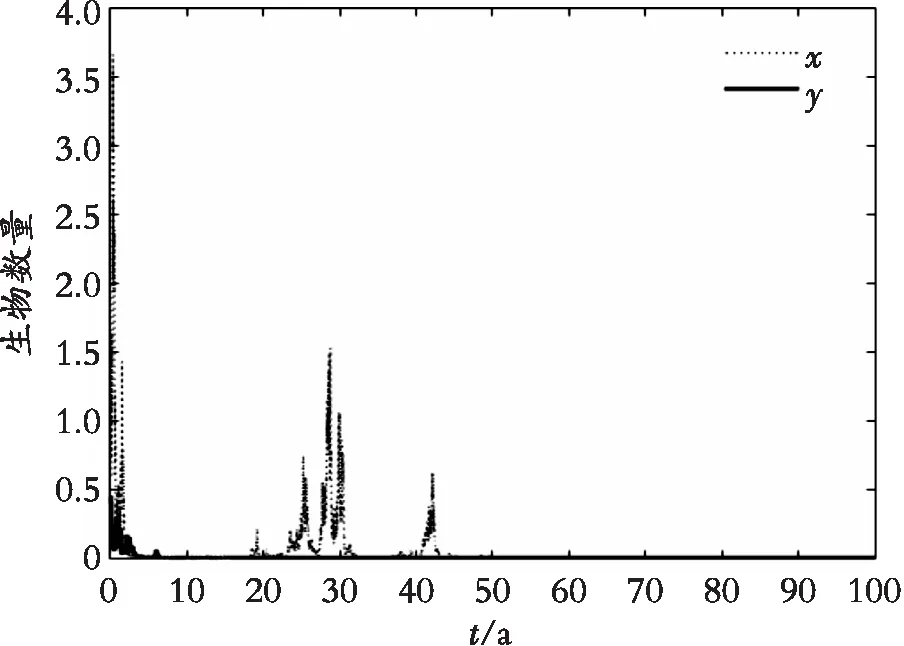
图3 强随机扰动下的生物数量图Fig. 3 Biological quantity diagram under strong stochastic disturbances with harvesting

4 结束语

提出一类具有代表性的非线性生物互惠模型，对其解的存在唯一性和遍历性进行说明，给出了物种持续存在与灭绝的条件，并且引入收获项展开对该系统最优收获问题的研究，算出最优收获效力。虽然模型仍存在一点不足，即由于模型的特性无法算出最优收获的一个具体值，但是通过计算出最优收获的一个范围，也能合理控制收获量以确保物种不至于过度捕获而灭绝。