饱和约束中立稳定多智能体系统有限时间广义一致性研究*
袁艺云, 王 慧, 曹 瑞, 王 霞, 韩 琦
(1.重庆师范大学 数学科学学院,重庆 401331; 2.重庆科技学院 电气工程学院,重庆 401331;3.重庆科技学院 智能技术与工程学院,重庆 401331)
0 引 言
近年来,多智能体系统的协调控制受到了广大科研人员的关注[1-3],特别是一致性问题。利用多智能体系统的一致性算法能解决智能电网的经济调度、动态负载平衡问题[4]。在多智能体网络中,单个智能体通过某个协议与系统中的其他智能体达成共识,即智能体的状态收敛于相同的值[5](一致值或群体决策值)。在目前的多智能体系统协调控制领域中,研究者大多采用分布式控制协议,因为相比于传统的集中式控制协议,分布式控制策略具有所用信息量少、协作性好、灵活性高等优点[6]。
许多学者对多智能体系统的一致性问题进行了研究,并进行了深入的讨论。文献[1]考虑如何提高智能体通信质量(降低通信量、提高通信信息利用率)的问题,设计了基于事件触发分布式控制协议;文献[3]研究了具有非线性动态和不确定扰动的多智能体系统一致性问题,设计了可以避免芝诺行为的分布式事件触发控制协议。但是多智能体系统在工业应用中却受到各种物理条件的限制,其中最常见的物理执行器具有饱和的特点(执行器工作范围的限制),比如电机的输出功率、转速等往往是有界的,若不考虑执行器饱和的特性,则可能会降低系统控制性能,从而导致系统不稳定。因此,考虑执行器饱和存在的情况十分必要。在文献[7]中, 提出了饱和受限的中立稳定无领导者多智能体系统的一致性算法。
在多智能体分布式控制中,高精度是评价一致性好坏的重要标准之一。在实际应用中,很多控制精度较高的系统,往往需要系统收敛的时间很短,这就导致了对有限时间一致性的探索。有限时间一致性是指各智能体在有限的时间内达到一个共同的状态。基于文献[7]、文献[8]设计了饱和受限的中立稳定多智能体系统有限时间一致性算法。这里不仅考虑了无领导者在无向拓扑图下的有限时间一致性问题,还考虑了领导-跟随多智能体系统在有向拓扑图下的有限时间一致性问题。
以上文献考虑的是多智能体系统完全一致性问题,实际上同步问题可以分为完全同步、广义同步和滞后同步[9]。广义同步即是在响应系统与驱动系统间建立一个函数关系。相比完全同步,广义同步具有更多的应用[10],如混沌系统的保密通信等。
基于上述文献的启发,考虑多智能体系统有限时间广义一致性问题是具有意义的。一方面,关于有限时间一致性的研究中饱和约束很少被考虑,另外一方面,目前很少有多智能体系统的有限时间广义一致的结果。本文的主要贡献如下:
1) 考虑了输入饱和约束的中立稳定多智能体系统的有限时间广义一致问题,相比较于文献[8],将完全一致问题转化为广义一致问题,丰富了文献[8]的研究。
2) 针对无领导者和领导-跟随二种情况提出了非光滑控制算法,并通过有限时间Lyapunov稳定理论、LaSalle不变集原理和不等式放缩、图论知识证明了在该控制算法下能实现有限时间广义一致,并得到了二种情况下的系统收敛时间的范围。
1 预备知识
1.1 符号说明

1.2 图论知识

1.3 问题描述
考虑带有N个节点的中立稳定多智能体系统:
(1)
其中xi∈Rn代表第i个智能体的状态,ui∈Rm代表第i个智能体的理想输入信号。
注1 由于式(1)是中立稳定的,因此所有A的特征值满足Re(λi)≤0,且Re(λi)=0时,其几何重数等于代数重数。
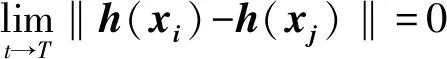
如果h(xi)=Pxi+Q,其中P∈Rn×n,Q∈Rn,则称式(1)能实现线性广义一致。
在给出主要结果之前,给出了一些假设和引理。
假设1 拓扑图是可连通的。
引理1[8]令vi∈R,vi>0,0 (1)V正定。 则系统能达到有限时间稳定,而且U0=U=Rn以及V(x)是径向无界的函数,则系统能达到全局有限时间稳定。 在本节中,提出了一个分布式一致性算法来解决无向图下无领导者多智能体系统的有限时间广义一致性问题。 对于式(1),存在一个非奇异线性变换xi=Wzi,使得系统式(1)变成如下形式: (2) 有限时间广义一致控制算法设计如下: (3) 其中:α∈(0,1),h(xi)=Pxi+Q,P1是正定矩阵。 定理1 对于在无向拓扑下具有N个节点的无领导者的多智能体系统式(1),当满足以下3个条件时,有 (PW)TP1(PW)=diag{Ic,P3} (4) P3As+AsTP3<0 (5) (6) 在控制算法式(3)下,式(1)可实现全局有限时间广义一致。 证明考虑如下的Lyapunov函数: (7) 容易得到V是径向无界的函数,将式(7)对时间求导可得 (8) 根据式(4),式(8)的第一项可变为 根据式(5)可以得到最后一个不等式。 式(8)的第二项,可化为 接下来,证明式(2)会在有限时间内收敛。当式(2)饱和未发生时,有 注意到 结合式(7)可以得到: V=eT(L⊗P1)e≤ λmax(L⊗P1)eTe≤ η1-1‖L⊗P1‖γTγ= 通过式(7)及引理1,有 注2 如果P=I,则控制算法式(3)可以解决系统式(1)在无向图下的有限时间一致性问题。 考虑一个由标记为0到N-1的智能体组成的多智能体系统,其中0是领导者,其余都是跟随者。 对于系统式(1),存在非奇异的线性变换zi=W-1(xi-x0),i=1,2,…,N-1,使得系统式(1)化为 (9) 对跟随者i=1,2,…,N-1,设计如下的控制算法: (10) 其中:Δ+κ≤μ。因此满足‖ui‖≤μ,系统式(9)可表述为下面的通式: 其中:u=[(u1-u0)T,…,(uN-1-u0)T]T,zm=[z1T,…,zN-1T]T。 定理2 在无向拓扑下具有N个智能体的领导-跟踪多智能体系统式(9),当满足以下条件时: (11) (12) 所设计的算法式(10)可以实现全局有限时间广义一致。 e=(L1⊗PW)zm 由于条件式(11)是成立的,因此对时间求导可得: 结合式(10),有 选取Lyapunov函数 V=eT(L1-1⊗P1)e 对时间求导可得: 由于条件式(12)成立,可化为 接下来将证明系统有限时间收敛。当饱和未发生时,有: 那么 V=eT(L1-1⊗P1)e≤λmax(L1-1⊗P1)eTe≤ 从而得到: 在这节中,给出两个例子来验证上述理论结果的正确性和有效性。 由于A的特征值为-0.321 8+0.714 1i,-0.289 7,-0.321 8-0.714 1i,则系统式(1)是中立稳定的。 图1 无领导者情形下的拓扑图Fig. 1 Communication topology without leader 图2 无领导者系统的误差ei演化图Fig. 2 Error variation of ei in the case of leaderless 图3 领导-跟随者系统的通信拓扑图Fig. 3 Communication topology of leader-following system 图4 领导-跟随者系统的误差ei演化图Fig. 4 Error variation of ei about the leader-following system

2 主要结果
2.1 无领导者情形







2.2 领导者-跟随者情形




3 数值仿真

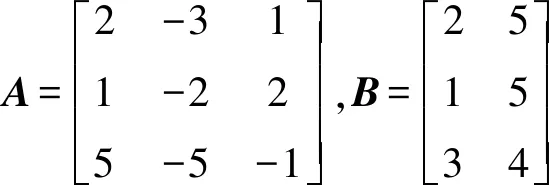







4 结 论


