基于旋量理论的三顶点刚性折纸可折叠性分析*

庄彦帅， 张 帆， 崔国华

(上海工程技术大学 机械与汽车工程学院，上海 201620)

0 引 言

折纸机构近年来发展迅速，它可以实现从二维平面到三维立体的运动转变。现在研究的折纸机构都为刚性折纸，即绕折痕旋转的面板为刚性的，且都在围绕刚性折纸的可折叠性进行科学探究。折纸机构有着丰富的数学理论[1]，日本的三浦公亮曾提出了著名的“三浦折叠”理论，该理论开始应用在包装太阳能电池板[2]，之后出现在一种全固态的可折叠超级电容器中[3]。折纸在应用领域方面开始被渐渐关注，在实用性上有了重大突破，但是缺乏对可折叠性的证明，于是在对刚性折纸可折叠性理论的证明上又引起众多研究者的探究。EVANS等[4]通过折纸二面角之间存在的关系与顶点配置来判断刚性折叠性，这种方法使得刚性折纸可折叠性研究可以从角度关系和配置类型方向探讨，为后续研究奠定了基础；WU等[5]利用四元数和对偶四元数来讨论刚性折纸可折叠性，后者可适用于分析多顶点折纸的可折叠性，提出了旋转矢量模型，并建立了一组特征矢量之间的环路封闭条件，可以有效地跟踪具有单个顶点或多个顶点的初始平面或非平坦的整个刚折叠过程。但是空间定点旋转的四元数理论应用范围非常有限，不适用于其他更多形态可折叠结构。CAI等[6]基于对偶四元数的方法，提出了顶点坐标转换方法来探究圆柱形折纸可折叠性，通过对多顶点折纸系统的QRS法来分析折角，利用对偶四元数计算所有顶点的坐标，可以检验刚性折纸折叠性，提出了新型的折纸机构即圆柱形折纸机构，但是由于多顶点折纸的折叠角和顶点坐标的复杂性较高，未能开发一种检测更多不同类型圆柱折纸算法；STERN等[7]通过寻找能量景观的基态来阐述自叠式折纸的折叠复杂性，指出了能量景观在纸张中可编程性的基本限制；ABEL等[8]提出一种线性时间算法来测试具有规定边缘长度和角度的平面图的可折叠性，以及一种多项式时间算法来计算不同折叠状态的数目，为开发其他算法提供了方向；SONG等[9]在梯形折痕的折叠运动学下，提出了折叠仿真算法和基本逆设计理论，还讨论了由两层可独立折叠或相容折叠的折叠环结构设计条件和程序，提出的框架在设计工程双曲结构中具有很高的应用价值，如飞机上双曲夹层结构的可展开圆顶和折叠芯；FENG等[10]研究了广义三角折纸的峰谷配置及导出的6R连杆，利用D-H法确定单顶点的角度关系，并拓展到三顶点折纸机构，确定了32种M-V配置方案，对用折纸刚性可折叠性进行判断。这些方法都是基于单个顶点的折纸模型，方法验证了单顶点的峰谷线配置、二面角及扇形角关系等，并拓展到多顶点的构型，提供了折纸机构可折叠性证明的数理关系，并开始将折纸与机构运动学建立联系。但是在对多顶点折纸机构的运动学分析方面还需要进一步探究，尤其是利用机构运动等效分析的方法还鲜有涉及。

在机构运动学分析中，利用运动旋量分析复杂的空间机构十分便捷，任一齐次变换矩阵T均可以表示为相应的运动旋量的矩阵指数[11]。旋量理论在闭环和并联机构的运动学分析上被普遍应用[12-14]。按照旋量的加法规则，旋量之间的原部与对偶部也线性相关。根据Grassmann线几何原理，可以根据线簇种类确定维数，并通过维数进一步确定线矢量线性相关性。偶量为自由矢量，方向相同即可线性相关。空间共点的一般旋量空间维度最大为6，最小为3[15]。综上所述，可以通过旋量之间的线性相关性来分析机构运动。

在单顶点折纸模型的基础上，利用现有的折纸配置及角度关系，提出通过运动学等效机构及旋量理论证明多顶点折纸机构刚性可折叠的方法。此方法将折纸与机构实现紧密联系，区别于以往的证明方法，从旋量理论的角度解释可折叠的折纸，由单顶点模型拓扑到三顶点折纸机构，对三顶点折纸进行运动学的机构等效与刚性可折叠性分析。首先将三顶点折纸机构运动学等效为3种6R闭环机构，并且固定其中一根连杆使之为定平台，将相对的连杆定义为动平台，该机构最终转化为拥有一个动平台与一个定平台的双支链6R闭环机构。计算出运动副的当前运动旋量，并由此建立速度方程，对运动副运动旋量间的线性相关性进行分析，当闭环内运动旋量之间线性无关，可证明闭环机构不具有可动性，即不可折叠。当运动旋量之间线性相关，进一步被动副可以线性表示出主动副，闭环机构瞬时速度不全为零，则可验证该机构具有可动性，即可折叠。利用机构学中的旋量理论，以运动学的角度，提出了一种解决三顶点折纸刚性可折叠性的验证方法，并解析三顶点折纸机构的折叠运动过程，分别验证三对折痕平行、一对折痕平行及全不平行的3种折纸构型的刚性可折叠性。以此为基础可以进行更多顶点的刚性折纸的研究，尤其以三顶点折纸的研究为理论，很容易扩展到其他类型的折纸图案，例如拥有四顶点折纸的正四边形的机构类型。对3种不同类型的三顶点折纸机构的刚性折叠性和机构运动学的深入研究为折纸机器人的模块化单元奠定了理论基础。折纸连续体机械臂需要满足单元模块间的可折叠，三顶点折纸机构的类型作为模块化单元在设计中具有很大的应用价值。

1 闭环机构运动学分析

1.1 关节运动旋量当前表示形式

旋量理论可以将物体的运动描述为绕某一定轴的转动和沿该轴的直线平移运动。根据旋量理论，闭链机器人运动学正解指数积公式可以表示为[11]

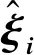
三顶点折纸机构可以运动学等效为6R连杆机构，运动学等效过程在下一节有具体表述。通过利用机器人运动学正解指数积公式表示出6个运动关节由初始状态下到经刚体变换后的位姿。由此可以建立机构末端速度与关节速度的线性关系[12]：

(1)

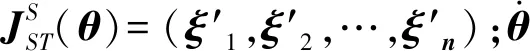
由此可以建立运动学等效的6R机构末端关节速度与其余各关节速度的线性关系，并进一步将运动方程与关节速度相联系。螺旋理论是探究机构关节的瞬时运动，所以需要得到变化的运动旋量，因此当前位形下单位运动旋量坐标有：

(2)

(3)

(4)

式(4)中：qi(0)为初始位形下轴线上一点的位置矢量。

可以写出运动学等效后6R连杆机构各关节当前位形下的运动旋量坐标，将得到的各关节当前位形下的运动旋量代入到所建立的速度方程中。

1.2 闭环机构的速度方程

将三顶点折纸机构运动学等效成6R连杆的闭环机构，在运动学中探究机构的运动特性往往是通过建立闭环机构的速度方程完成的。将其中一杆件固定，另一杆件作为运动平台，便形成了两支链的并联机构。将当前位形下机器人各关节的运动旋量坐标代入式(1)中，得到并联机构的闭环速度方程为

(5)

得到当前的向量方程形式：

(6)

进一步可以整理为

(7)

将三顶点折纸机构首先运动学等效为6R连杆闭环机构，又根据该折纸运动形式将其分解为双支链的闭环机构，从而构成并联机构。对于并联机构来说，各个支链所连接的末端执行器的位姿是相同的，因此建立了如式(7)所示的闭环机构的速度方程，其中ξnn表示第n条支链的第n个关节的运动旋量；θnn表示为第n条支链的第n个关节的关节变量。求解由位姿方程得到的速度方程，来探究简化的6R闭环机构6关节运动旋量之间的线性相关性，通过对运动副的运动旋量之间的线性相关性判断，来确定运动学等效机构的可动性，再基于Grassmann线几何原理，得到不同类型刚性折纸机构的维数，从而确定不同类型折纸机构的刚性可折叠性。

2 机构等效与约束关系

2.1 机构等效

三顶点折纸机构具有3种形式结构，即具有三对折痕平行、一对折痕平行和每个折痕都不平行的情况。折纸机构可运动学等效为一个闭环机构，以三对折痕平行的折纸(图1)为例，实线为峰线，虚线为谷线，每条折痕可等效为转动副(图2)，刚性板等效为连杆，中间板可不予考虑，将其中一杆件固定形成定平台，选择其中一杆为动平台，于是可以形成拥有两条支链并联的闭环机构(图3(a))。假设在此闭环机构中，R11为主动副，其余为被动副，用同样方法也可得到一对折痕平行与折痕均不平行的两种构型等效机构即图3(b)和3(c)，找到机构关节间的关系，并建立基坐标系和工具坐标系。

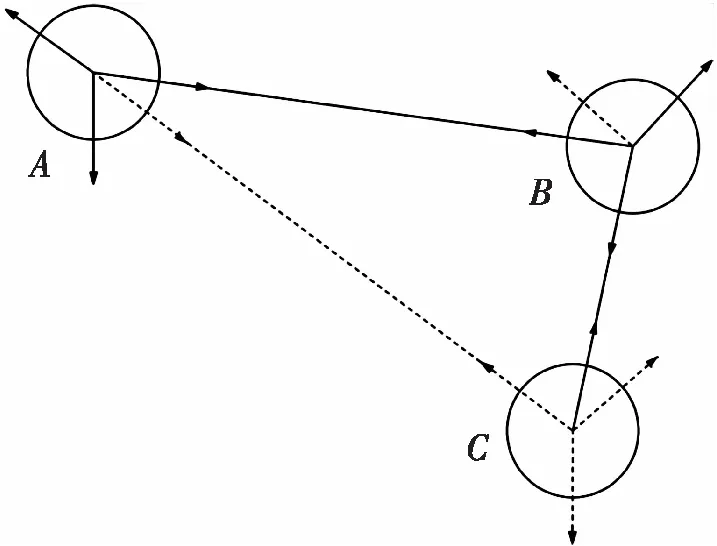
图1 三对折痕平行折纸Fig. 1 Three pairs of creases parallel origami

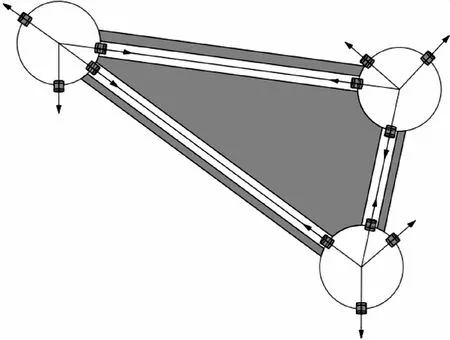
图2 折痕等效转动副Fig. 2 The equivalent rotating pair of crease

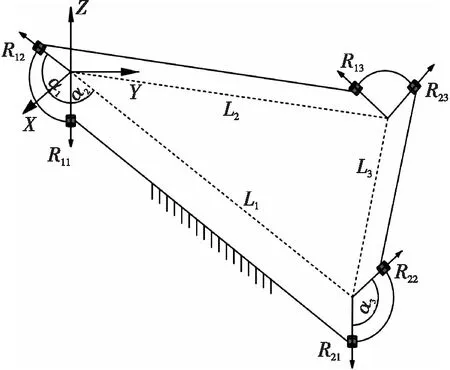
(a) 三对折痕平行

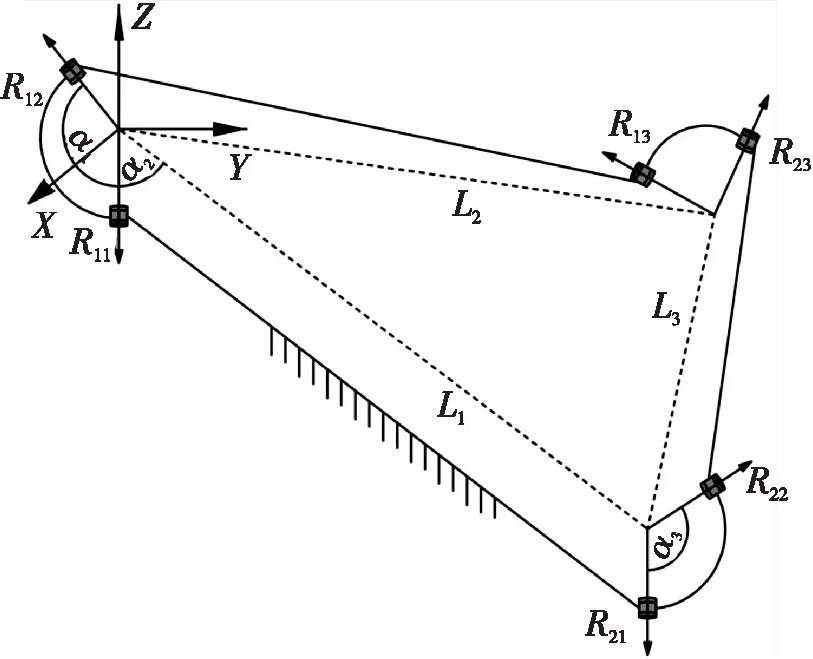
(b) 一对折痕平行

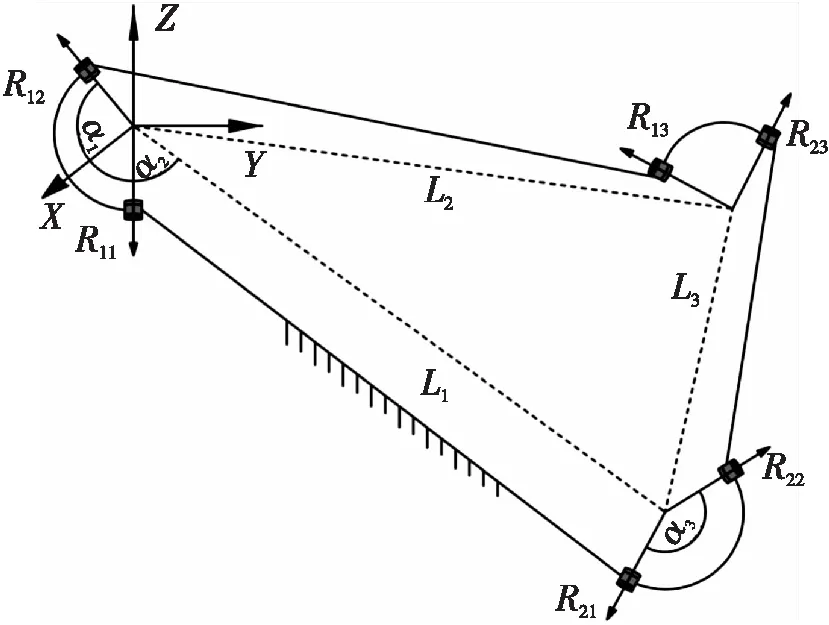
(c) 折痕均不平行

图3中αi为关节间扇形角，其中i=1，2，3。

(1) 三对折痕平行的6杆机构关节轴线之间存在如下关系：

关节轴线的平行关系：R11∥R21，R12∥R13，R23∥R22；关节轴线的共点关系：R11与R12，R13与R23，R21与R22共点。

(2) 一对折痕平行的6杆机构关节轴线之间存在如下关系：

关节轴线的平行关系：R11∥R21；关节轴线的共点关系：R11与R12，R13与R23，R21与R22共点。

(3) 折痕均不平行的6杆机构关节轴线之间存在如下关系：

关节轴线的平行关系：不存在；关节轴线的共点关系：R11与R12，R13与R23，R21与R22共点。

2.2 约束关系

2.2.1 单顶点折纸机构峰线谷线的角度关系

由单顶点折纸机构的角度关系推导出三顶点折纸机构之间的角度关系，以此来进行角度之间的换算求导。虚线表示谷线，实线表示峰线，单顶点折纸机构峰线与谷线部分类型如图4所示。

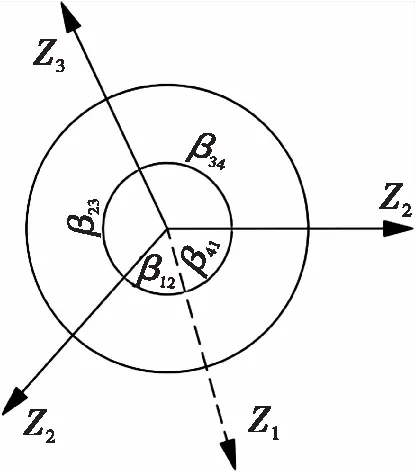
(a) 类型一

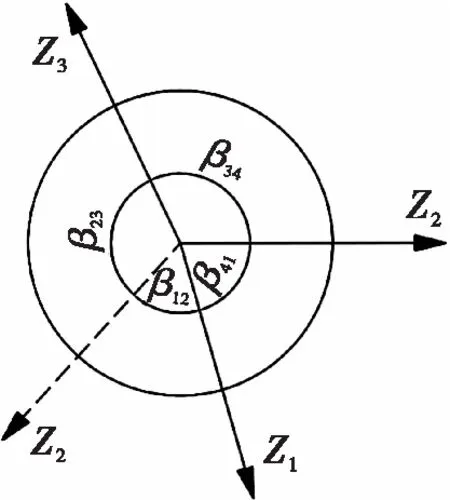
(b) 类型二

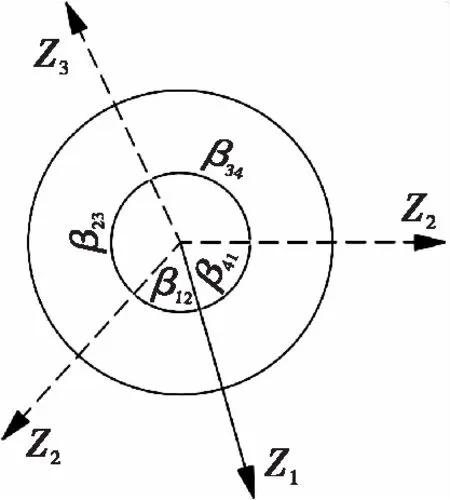
(c) 类型三

单顶点折纸机构峰线谷线的配置类型在扇形角和关节旋转角上存在一定的关系，这些角度关系在分析机构中有重要作用。

在图4(a)与在图4(c)中有：

β23+β41=π，β12+β34=π，θ1=-θ3，θ2=θ4

(8)

在图4(b)中有：

β23+β41=π，β12+β34=π，θ1=θ3，θ2=θ4

(9)

其中：β为扇形角；θ为关节旋转角。

2.2.2 三顶点折纸机构峰线谷线的角度关系

三顶点折纸机构峰线谷线之间的角度关系可由单顶点折纸机构峰线谷线的角度关系得到。

三顶点折纸机构的折线配置类型如图5所示，虚线表示谷线，实线表示峰线。由图5所示，3个单顶点峰线谷线配置类型符合图4所示类型，A顶点符合类型一，B顶点符合类型二，C顶点符合类型三，由式(8)和式(9)所示得到角度关系：

(10)

进一步，由式(10)所示，可知关节旋转角的角度关系：

θ12=-θ22，θ13=θ21，θ11=θ23

(11)

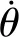
(12)

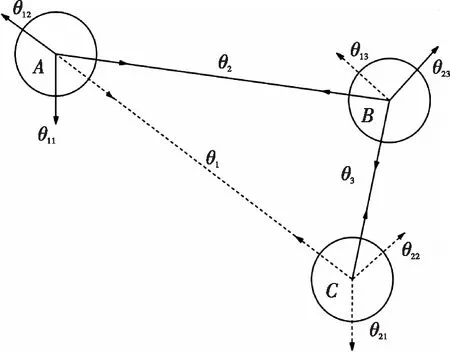
图5 三顶点折纸机构峰线谷线配置类型Fig. 5 Peak-line and valley-line configuration type of three-vertex origami mechanism

3 机构线性关系与可折叠性分析

3.1 三对折痕平行机构的分析

将闭环机构分成两个支链，根据式(2)、式(3)和式(4)，写出当前位形下各个关节对应的运动副旋量坐标如下：

一条轴线的运动旋量可以用仅有原部和偶部的矢量来进行表示：

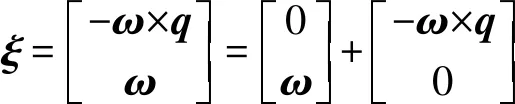
(13)

其中：

X1=L2[-sα2cα3sθ11sθ12+cθ12sα2(cα1cα3cθ11-

sα1sα3cθ21)-cα2(sα1cα3cθ11+cα1sα3cθ21)]

X2=L2[-sα2cα3cθ11sθ12+cθ12sα2(sα1sα3sα21-

cα1cα3sθ11)+cα2(sα1cα3sθ11+cα1sα3sθ21)]

X3=L2sα3[-sα2sθ12c(θ11-θ12)+cα1sα2cθ12c(θ11+

θ21)+sα1cα2s(θ11-θ21)]

由式(7)(12)和(13)可以得到：

整理得到：

(14)

进行赋值运算，即

(15)

将式(15)代入式(14)得到如式(16)所示：

(16)

将计算出的当前位形下的运动旋量坐标代入式(16)，即可以得到具体的表达式，由于结构式太长，不再进行具体表述。以式(16)所示进行分析，等式右侧是由两个过原点的原部与4个空间偶部组成。根据Grassmann线几何原理，空间共点条件下任意多条线矢量所组成的集合维数为3，即构成三维线簇。因此共点的3个转动副是可以线性表示另一单一转动，而此式仅存在两个共点的转动副，其维数仅为2，无法线性表示另一转动。由于偶量为自由矢量，方向相同的偶量即可线性相关，且维数最大为3，此式存在4个空间偶部，是线性相关的。综合原部与对偶部的分析，此结构式无法求出满足速度方程的解，进一步无法积分得到位姿方程的解，该机构不具有可动性，即三对折痕平行的折纸类型是不可以折叠的。

3.2 一对折痕平行机构的分析

根据式(2)(3)(4)和式(13)所示，写出当前位形下各个关节对应的运动旋量坐标：

将当前位形下各个关节对应的运动旋量坐标与式(12)代入式(7)，可得到：

整理得到：

(17)

将系数相同的矢量合并：

(18)

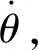
3.3 折痕均不平行机构的分析

根据式(2)(3)(4)和(13)所示，写出当前位形下各个关节对应的运动旋量坐标：

将当前位形下各个关节对应的运动旋量坐标与式(12)代入式(7)可得到：

整理得到：

(19)

将系数相同的矢量合并：

(20)

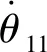
4 结 论

将三顶点折纸机构运动学等效为成双支链闭环的6R机构，根据并联机构支链的特点，结合运动学中的旋量理论，建立了闭环机构的速度方程，通过运动旋量间的线性相关性来证明机构的可动性，即证明折纸机构的可折叠性。三顶点折纸机构有多种峰线谷线的配置类型，会存在不同的扇形角，都可以通过本文的运动学等效机构方法，将折痕等效为转动副，刚性板等效为连杆，从而建立仅存在转动副的连杆机构。以运动旋量线性相关性的角度来探究折纸机构的可折叠性，并以运动学等效的机构为模型，进行下一步的运动仿真。不同参数类型的多顶点折纸机构是否可折叠，则需要将具体数值代入速度方程中判断是否存在相应系数，以验证该类型的可折叠性。可依据此验证方法，来探究三顶点以上的多顶点刚性折纸机构的可折叠性，并以三顶点折纸机构为模型，提供了折纸机器人模块化单元设计的基础理论。