我国城市建设水平研究*
陈瑜鑫, 刘惠篮
(贵州大学 数学与统计学院, 贵阳 550025)
0 引 言
由于社会和自然因素影响,我国各地区的城市建设情况及设施水平发展不均衡。本次研究的主要目的是对城市建设情况及设施水平的相关数据进行分析,从而得出各地区城市建设水平的综合得分,更好地了解各地区城市建设情况与设施水平的差异。
近年来,众多研究人员对城市设施水平进行了比较研究,得出了一些研究成果。2004年,李凤琴[1]选取了与城市设施水平有关的7个变量,在因子分析的基础上,结合聚类分析对各地区城市设施水平进行评价,由聚类分析的结果将这些地区分成3类,最终得到了城市设施水平的大致情况;2008年,张哲等[2]针对全国31个城市基础设施建设数据,运用聚类分析和主成分分析进行实证研究,结论表明:基础设施建设水平较高的是经济发达的北京、上海等城市,相对于南方城市而言,北方城市的建设水平普遍较低;2013年,谢英欣等[3]基于K-均值法对我国各地区城市基础设施建设水平进行聚类,分析我国东部和西部地区城市基础设施建设不均衡的具体因素,提出政府要充分发挥宏观调控的作用,加大对我国中西部地区城市的政策帮助和资金投入,加快改善中西部落后省份城市的基础设施建设水平;2015年,张伟芳等[4]选取了甘肃省各城市10年的基础设施数据,运用变异系数法计算各州市的城市基础设施得分,通过图表描绘了各城市基础设施的改变,得出了甘肃省14个州市基础设施建设水平的发展存在明显差异,从3个方面分析了城市基础设施的影响因素;2016年,荣月静等[5]选取长江三角洲地区16个城市基础设施建设的数据,基于多因素综合评价等方法对该地区的城市基础设施建设水平进行研究,提出城市基础设施的各个方面要协调发展,同时也指明各城市在基础设施发展过程中存在的问题,并提出与之相对应的解决方法,期望长江三角洲各个城市的基础设施建设为其他城市提供一定的经验;2017年,朱怡然[6]选择了城市桥梁、绿地面积、用水普及率等22个指标对全国31个省市自治区的城市竞争力进行评价,利用主成分分析选取了前4个主成分并得到31个省市自治区的综合得分,根据综合得分将这些地区进行排序,对城市建设水平较低的地区给出了一些很有针对性的建议。
对于城市建设水平的研究,上述学者建立了比较完善的评价指标体系,为研究最新的城市建设水平提供了坚实的基础。采用不同的多元统计方法研究各地区城市建设及设施水平,得到了不同地区城市建设水平发展的具体情况,针对各地区城市建设水平的差异,提出了与之相对应的解决对策。但是以上研究大多基于主成分分析和因子分析等传统多元统计方法,在某些情形下难以解释。稀疏主成分方法极大地稀疏了载荷矩阵,因此,它相较于主成分方法具有更强的可解释性。通过平衡主成分的稀疏度和解释程度,讨论了惩罚参数的选择方法。
本文基于稀疏主成分法与聚类方法对2017年和2018年城市建设情况及设施水平的数据进行研究,深入了解各地区城市建设情况与设施水平的差异,得到了2017年到2018年城市建设水平的动态变化,这些有意义的结论将促进城市的建设与发展。
1 建立模型
1.1 主成分
主成分分析[7]是在保留绝大多数信息量的条件下,通过线性变换的方式,用较少的新变量替代原来较多的变量。它的实质就是通过原始变量的线性组合来达到降低原始变量维度的目的,主成分就是经过变换后得到的新变量。主成分与原始变量之间存在以下的关系:各主成分之间互不相关,原始变量的数量大于主成分的数量,多个原始变量的不同线性组合构成了不同的主成分,选取的主成分只损失了原始变量很少部分信息。
设X=(X1,X2,…,Xp)T是p维随机向量,均值E(X)=μ,协方差阵Cov(X,X)=∑。考虑以下的线性变换:
容易看到:
为了得到较好的结果,希望Zi的方差比较大,同时Zi之间是互相独立的,由于
对于任意的常数c,有
从上面的式子可以看出,对ai不加限制时,Var(Zi)将会变得任意大,这样,所研究的问题将变得没有意义。因此,有下面的约定:

(2)Zi与Zj相互无关,i≠j,i,j=1,2,…,p。

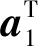
等式两边分别对a1和λ求导,并令其等于0
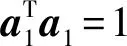
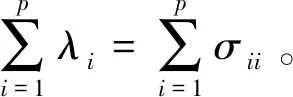
另外,主成分的选取个数可以由特征值的变化情况来确定,可以利用R软件画出碎石图,通过图形的变化趋势来确定主成分的个数m。由相关阵R求主成分的过程与由协方差阵∑求主成分的过程是一致的,这是因为X的相关阵刚好是X*的协方差阵,X*是原始变量经过标准化处理后的变量。
1.2 稀疏主成分
Zou等[8]提出了稀疏主成分分析方法,稀疏主成分是建立在主成分可以写成一个二次惩罚的回归型优化问题的基础上的,Lasso[9]惩罚和Elastic Net[10]可以直接整合到回归准则中,从而实现模型具有稀疏加载的主成分。稀疏加载后的主成分,使得载荷矩阵的一部分变量系数压缩为零,不仅提高了模型的可解释性,而且稀疏主成分能正确地识别重要的变量,不会丢失重要变量的信息。通常情况下,稀疏主成分的求解能转化为如下的优化问题:
s.t.ATA=Ik×k
其中:Xi表示原始矩阵的第i列。下面的算法总结了稀疏主成分的求解步骤:
Step1令A初始化为前k个普通主成分的载荷向量V[,1:k]。
Step2对于固定的A=[α1,…,αk],其中αi,i=1,2,…,k表示前k个主成分的载荷向量,解下面的Elastic Net问题:
其中j=1,2,…,k。
Step3对于固定的B=[β1,β2,…,βk],其中,βi,i=1,2,…,k表示前k个稀疏主成分的载荷矩阵。计算SVD分解XTXB=UDVT,然后更新A=UVT。
Step4重复第二步至第三步,直到收敛为止。
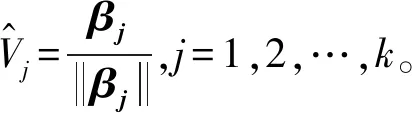
通常可以使用LARS-EN算法求解步骤2中的Elastic Net问题,从而得到合适的惩罚系数。同时LARS-EN算法很大程度上提高了稀疏主成分的计算效率。
准确地选择惩罚系数对求解主成分是极其关键的,当n>p时,η通常被选取为零,不同的η1,j可以得到不同的稀疏主成分。本文选择惩罚系数时,不仅要考虑主成分的稀疏度,同时也必须兼顾主成分对于原始变量的解释程度[11]。令M表示载荷为零的变量个数,N代表总变量个数,PEV表示方差解释程度。定义S为
用解释方差度刻画解释程度,本文考虑S达到最大时所对应的η1,j值是最优的惩罚系数。
1.3 聚类分析
作为一种常用的多元统计方法,聚类分析将样品进行分类,根据样品之间的相似性,把相似度越高,差异越小的样品聚为一类,使得同一类中样品相似度高,不同类之间样品相似度低。这里主要研究的是Q型聚类分析。研究样品之间的关系是对样品进行聚类的前提,有许多统计量可以用来描述样品间的相似程度,一般用得比较多的统计量就是距离。样品Xi与Xj之间的距离用dij来表示,一般有下面的要求:
(1)dij≥0,∀i,j;dij=0⟺Xi=Xj。
(2)dij=dji,∀i,j。
(3)dij≤dik+dkj,∀i,j,k。
此处使用的样品间的距离是欧式距离。其定义为
在众多聚类方法中,应用最为广泛的就是系统聚类法,系统聚类法的聚类过程可以由谱系图最终表示出来。系统聚类法的步骤如下:
Step1计算n个样品两两之间的距离。
Step2将n个样品对应于n个类,保证每个类只包括一个样品。
Step3将n个类中距离最接近的两个类合成一个新的类。
Step4计算已有的各类与最新得到的类之间的距离;观察类的个数是否为1。如果不是,重复步骤3和4;若是,则转到步骤5。
Step5画出谱系聚类图。
Step6决定分类的个数和聚类的成员。
2 实证分析
本文使用的数据为目前所有的最新数据,来源于2018年和2019年中国统计年鉴,各地区城市建设情况及设施水平的统计指标见表1。首先采用稀疏主成分方法对2018年各地区的城市建设情况及设施水平进行评价,利用该方法计算各地区的综合得分,按综合得分的高低进行排序。仅选取一年的城市建设水平数据进行分析,只能了解这些地区该年度的城市建设情况,无法更好地了解城市发展的趋势。因此,将2017年和2018年我国各地区的综合得分进行对比,得出两年间我国城市建设情况及设施水平的变化趋势。同时运用系统聚类法对全国31个省市自治区分类。

表1 城市建设水平评价指标Table 1 Evaluation index of urban construction level
由于各个评价指标的单位不一致,而且指标的量级差距较大,所以本文在使用主成分分析(表2)和稀疏主成分分析之前,需要对数据进行标准化处理。通过稀疏主成分分析法,可以得到前5个稀疏主成分的载荷矩阵、贡献率、累积贡献率,惩罚系数η1,j=(0.3,0.6,0.2,1,0.6)对应于不同的稀疏主成分。稀疏化后的载荷矩阵如表3所示。
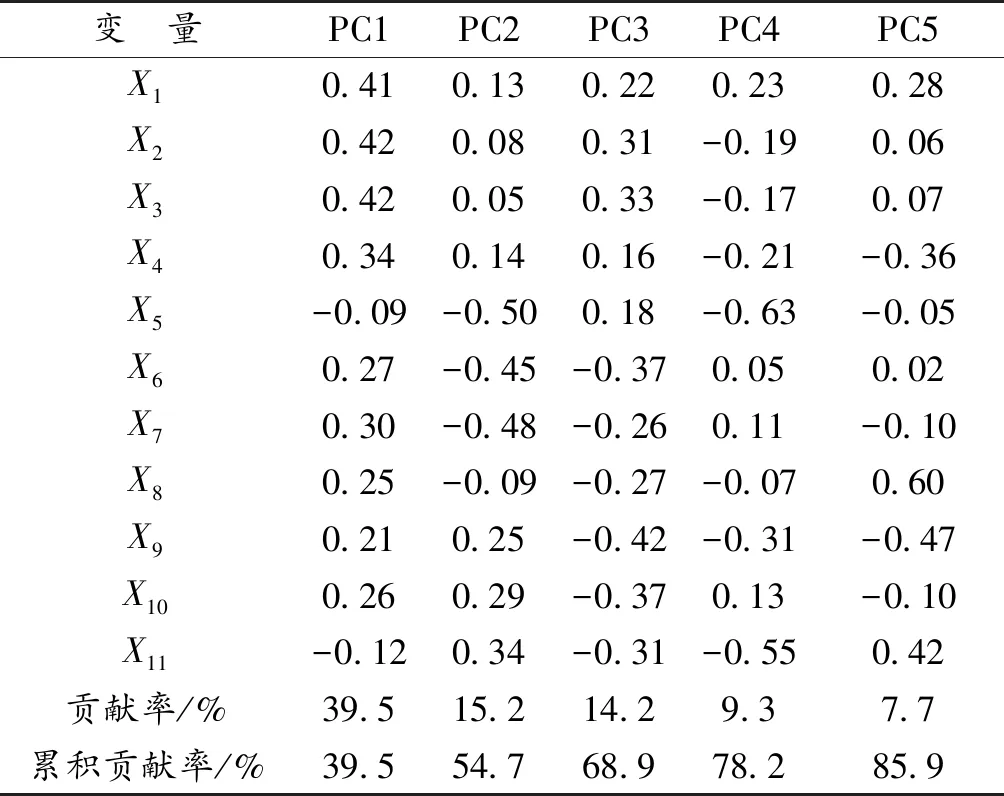
表2 主成分的载荷矩阵Table 2 Loading matrix of principal components
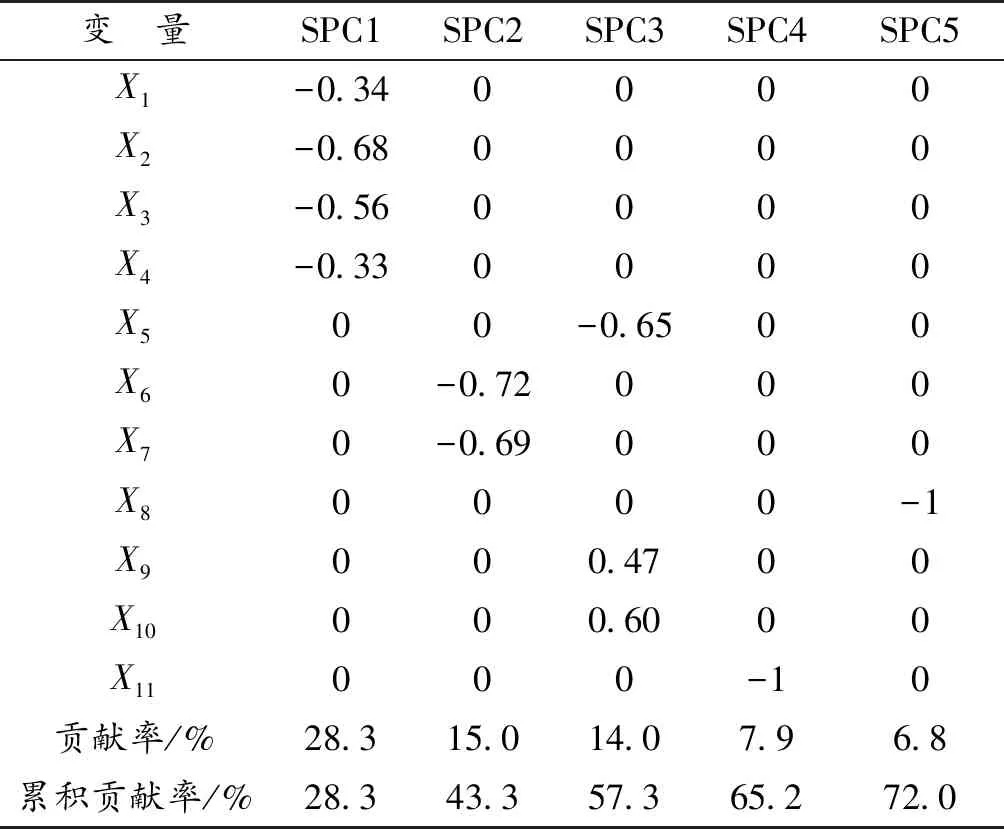
表3 稀疏主成分的载荷矩阵Table 3 Loading matrix of sparse principal components
城区面积、建成区面积、城市建设用地面积、征用土地面积的综合就是第一主成分,第一主成分主要代表城市建设中的面积;第二主成分为水气主成分,主要与城市用水普及率和城市燃气普及率相关;第三主成分为人均面积及密度主成分,主要表示的是人均城市道路面积、人均公园绿地面积和城市人口密度;第四主成分和第五主成分中,由于其他变量的系数被压缩为零,分别只剩下一个变量的系数非零,因此,第四主成分表示每万人拥有公共厕所;第五主成分表示每万人拥有公共交通车辆。
由主成分和稀疏主成分载荷矩阵的对比分析来看,使用稀疏主成分极大地稀疏了载荷矩阵,使得每个主成分所对应的部分变量系数被压缩为0。由表3可知,前5个稀疏主成分的方差贡献率逐渐减少,保留了原始变量72.0%的信息,同时极大地稀疏了载荷变量的个数。第一主成分中,载荷为0的变量个数有7个,第二主成分中,载荷为0的变量个数有9个,第三主成分中,载荷为0的变量个数有8个,第四主成分和第五主成分中,载荷为0的变量个数都有10个。利用稀疏主成分对各地区城市建设情况及设施水平进行分析,可以得到各地区的综合得分及排名如表4所示。值得注意的是,表4中综合得分负得越大,综合得分越高。
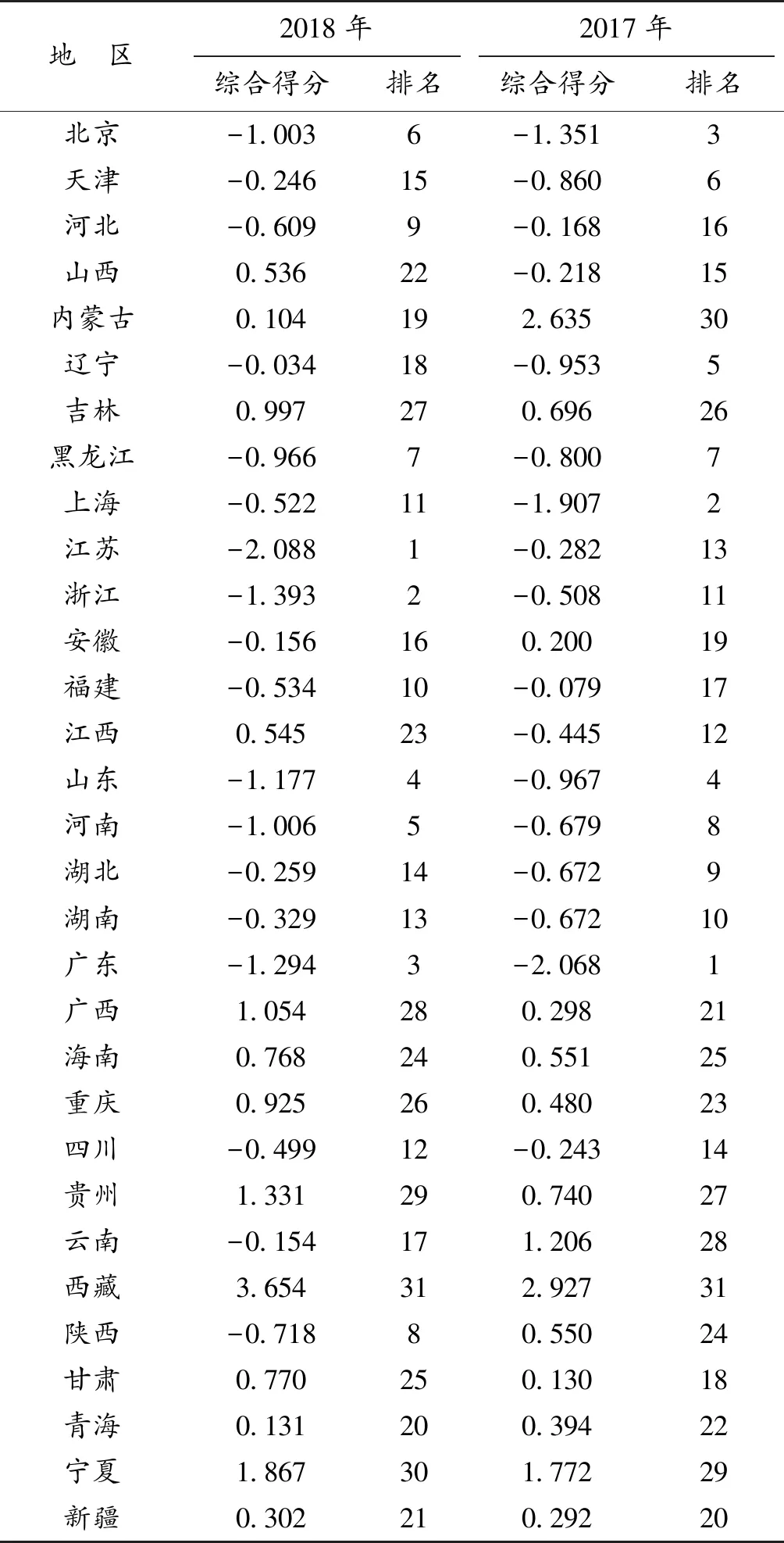
表4 各地区城市建设水平综合得分及排名Table 4 Comprehensive score and ranking of urban construction level in various regions
从表4可以看到2018年我国各地区城市建设与设施水平的大致情况,具体表现在以下几个方面:综合得分排名靠前的10个地区分别是江苏、浙江、广东、山东、河南、北京、黑龙江、陕西、河北、福建,表明这10个地区的城市建设情况及设施水平较高。综合得分排名第11至21名的地区分别为上海、四川、湖南等11个地区,表明这些地区的城市建设情况及设施在国内处于中等水平,其他10个地区的综合得分排名是比较靠后的,这10个地区的城市建设情况及设施水平与全国其他各地区存在一定的差距。
从2017年与2018年的各地区城市建设情况及设施水平的对比分析来看,综合得分排名呈上升趋势的地区有12个,分别是河北、内蒙古、江苏、浙江、安徽、福建、河南、海南、四川、云南、陕西、青海。这12个地区中,陕西、江苏、内蒙古和云南的上升幅度是非常明显的,陕西的综合得分排名从2017年的第24名上升到了第8名,江苏次之,从2017年的第13名上升到了第1名,内蒙古的综合得分排名从第30名上升到了第19名,云南的综合得分排名也上升到了第17名。这4个地区的城区面积、建成区面积都有了较大幅度的增长,导致了它们的综合排名有了较为明显的提升。这两年间,综合得分排名保持不变的地区共有3个,依次是山东、黑龙江和西藏。由表3可以看出,山东和黑龙江的综合得分在2017年和2018年都是比较靠前的,其中,山东的综合得分排名为第4名,黑龙江的综合得分排名为第7名,西藏的综合得分最低,它的综合得分排名为第31名。综合得分排名呈下降趋势的地区有16个,分别是广东、上海、北京、辽宁、天津、湖北、湖南、江西、山西、甘肃、新疆、广西、重庆、贵州、吉林、宁夏。这16个地区中,辽宁、江西的下降幅度比较明显,辽宁的综合得分排名从2017年的第5名降到了2018年的第18名,江西的综合得分排名从2017年的第12名下降到了2018年的第23名。
由于各变量的量纲不一致,所以使用标准化后的数据进行分析,计算关于欧式距离的距离矩阵,得到各个样品之间的距离。对2018年各地区城市建设水平的相关数据选择离差平方和法进行系统聚类,可以将31个地区分为3类,聚类结果见图1。第一类包括广东、江苏、山东;第二类包括天津、上海、云南、陕西、黑龙江、河南、湖南、新疆、河北、福建、海南、青海、江西、山西、贵州、甘肃、内蒙古、宁夏、北京、浙江、安徽、四川、辽宁、湖北、广西、吉林、重庆;第三类包括西藏。
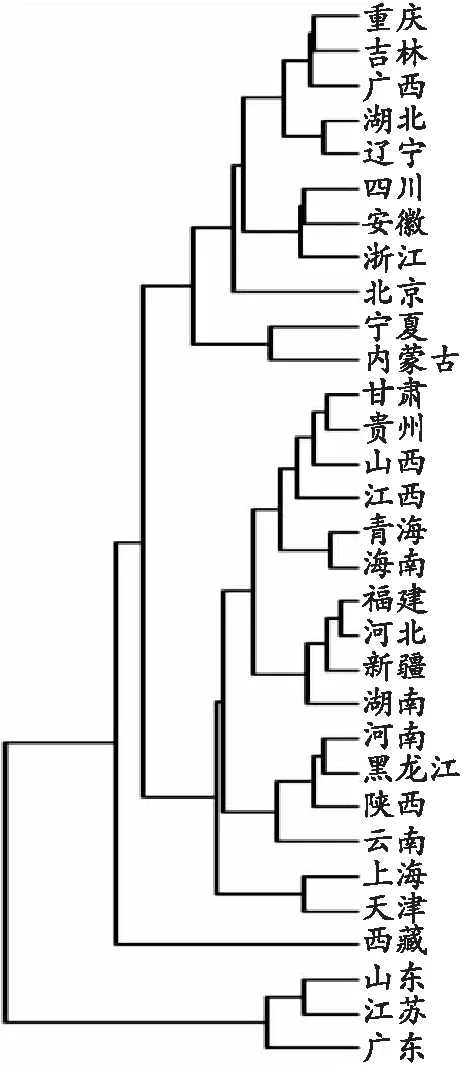
图1 系统聚类图Fig. 1 Hierarchical clustering diagram
运用稀疏主成分法与系统聚类法对2018年城市建设水平进行综合评价,第一类的3个地区的综合得分排名都比较靠前,第二类地区的综合得分排名居中,第三类的西藏地区综合得分排名最后。这也说明了由稀疏主成分得到的综合得分排名是合理的。
3 结论与建议
从2018年各地区综合得分的排名来看,我国各地区城市建设及设施水平的发展是存在差异的,总体趋势是东部沿海地区的水平普遍较高,尤其是江苏、浙江、广东、山东的城市建设水平稳居前列;西南和西北内陆地区的城市建设及设施水平较低,特别是西藏、宁夏、贵州与其他地区的水平存在较大的差距。为了保证各地区城市建设水平更加均衡地发展,更好地推进我国城市建设的进程,在此,提出如下几点建议:
综合得分排名名列前茅的4个地区分别是江苏、浙江、广东、山东,从它们所处的地理位置来看,这几个省都处于我国东部沿海地区,它们的城市建设及设施水平在全国处于领先。东部沿海地区城市建设水平迅速崛起的重要原因在于它们天然的地理优势,改革开放初期,首先发展沿海的策略使得这些地区的城市化水平较高,所以,东部沿海地区要保持现在的发展势头,继续巩固现存的发展优势,树立可持续发展理念,实现城市建设又好又快发展;同时要给其他地区的城市建设树立典范,为全国各地区的城市建设提供宝贵的经验。
综合得分排名处于中间位置的这些地区,它们的城市建设及设施水平在全国范围内处于中等。这些地区要向城市建设较好的东部沿海地区看齐,争取与东部沿海地区的城市建设水平接近,让自身的城市建设迈上一个新的台阶,实现的跨越式发展。其中,上海和四川的城市建设水平发展极其显著,其他的地区要积极借鉴这两个地区的城市建设经验,不断提高城市建设水平。
在错综复杂的因素影响下,西南地区和西北地区的城市建设水平是较低的,尤其是西藏、宁夏、贵州的城市建设长期处于较低水平。这几个地区位于我国的内陆地区,不仅自身经济实力相对偏弱,而且得到政府的资金帮助有限。因此,西南、西北地区要根据自身优势,因地制宜地发展经济,从而保证城市建设有源源不断的资金支持。同时要充分认识到与其他地区城市建设与设施水平发展的差距,从其他地区吸取经验,摆脱城市建设情况较差的面貌,实现我国各地区城市建设的均衡发展。

