二次分式函数的n次迭代问题*

魏 小 琴

(重庆师范大学 数学科学学院，重庆 401331)

0 前 言

离散动力系统是对常微分方程解族进行离散化之后得到的系统。因其形式简洁并易于反映问题的本质，从20世纪60年代开始在Smale等著名数学家的倡导下蓬勃发展起来。对函数n次迭代的研究有助于了解离散动力系统轨道的长期行为。具体地说， 函数f(x)的迭代[1]是指对同一函数f(x)的多次复合。f(x)的n次迭代记为

对于函数的迭代，人们比较关心它的n次迭代式。如何求得函数的n次迭代式，就成为人们不断研究的课题。

目前，已有的方法有不动点法[1]、矩阵法[2-3]、共轭相似法[1,4]。根据函数的不同，可以选择更为适合它的方法去求解n次迭代式。文献[1]用不动点法求解一次函数f(x)=ax+b的n次迭代式， 得到

不动点法的原理是通过设置待定系数，利用函数f(x)的不动点计算出待定系数，进而求得函数f(x)的n次迭代式[1]。方法针对求解一次函数的n次迭代式非常适合，当然，不动点法还可以用于二次函数、线性分式函数，但却不是唯一最优的方法，对于线性分式函数：

文献[3]利用矩阵法讨论它的n次迭代。文献[4]则利用矩阵的特征多项式的理论，推广了前人已有的结论，并得到了计算线性分式函数n次迭代式的一般公式。矩阵法的原理是首先定义线性分式函数的系数矩阵，再根据数学归纳知，可以将求解线性分式函数的n次迭代问题转化为计算系数矩阵的n次幂问题[3]。利用此方法，文献[5]用共轭相似法求解二次函数f(x)=ax2+bx+c的n次迭代式， 得到

共轭相似法的原理是通过可逆桥函数h(x)，使函数f与g满足f=h-1∘g∘h，把一个复杂函数转化成一个易求迭代式的较为简单的函数。再求出简单函数的n次迭代式，并利用fn=h-1∘gn∘h这一性质，进而求解出原函数的n次迭代式[1-2]。共轭相似法的关键是桥函数， 但这没有一个固定的方法。

关于二次分式函数：

(1)

已有若干的研究成果。如文献[6]给出二次分式函数在两种情形b1=c1=b2=0且a1∶a2∶c2=1∶2∶-1以及a1=c1=b2=0且b1∶a2∶c2=2∶-1∶1下的n次迭代式结论，文献[7]给出二次分式函数在两种情形a2=b1=0且a1∶b2=1∶2以及c1=b2=0且b1∶c2=2∶1下的n次迭代式结论。这些都是二次分式函数的一些特殊情形，如何扩大更多特殊情形的二次分式函数的n次迭代式，得到更多的结果，就成为探究的重点。二次分式函数有很多的特殊情形，主要关注a2b2c2≠0的情形，并针对未解决的3种的情形进行研究，即：

(i) 若b1=0且a1c1=0时；

(ii) 若b1≠0且a1c1=0时；

(iii) 若a1b1c1≠0且满足：

a1=a2+1，b2=b1+2，c1=c2+1

将通过对不同特殊情形下的二次分式函数选取不同的桥函数， 利用共轭相似法求解得出结论。

1 主要结果及证明

定理1 若b1=0且a1c1=0时，二次分式函数如式(1)所示可转化为

其中式(2)的n次迭代式为

式(3)的n次迭代式为

证明先证式(2)的n次迭代式， 取桥函数h(x)=1/x， 则h-1(x)=1/x， 于是由共轭相似f(x)=h-1∘g∘h(x)可得

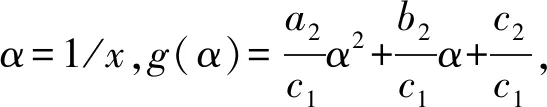
最后由fn(x)=h-1∘g∘h(x)可得fn(x)。

式(3)的证明与式(1)的证明类似。同样取桥函数h(x)=1/x，则h-1(x)=1/x，通过共轭相似可得到：

再根据二次函数已有的n次迭代式知：

最后由fn(x)=h-1∘gn∘h(x)可得fn(x)。

定理2 若b1≠0且a1c1=0时， 二次分式函数如式(1)所示可转化为

若式(4)满足a2=1，b1=b2+2，c2=c1+1，也即是形如

(6)

其中B≠-2，C≠0。它的n次迭代式为

其中

η2(α(B，C)，β(B，C))=

且α(B，C)=B+C+2，β(B，C)=B+2。

若式(5)满足c2=-1，a1=a2+1，b2=b1+2， 也即是形如

(7)

其中,A≠-1，B≠0。它的n次迭代式为

其中

η4(μ(A，B)，ν(A，B))=

且μ(A，B)=A+B+1，ν(A，B)=2A+B+2。

证明先证式(6)的n次迭代式，取桥函数h(x)=1/(x-1)，则h-1(x)=1/x+1。由共轭相似f(x)=h-1∘g∘h(x)得

g(x)=h∘f∘h-1(x)=-(B+C+2)x2-(B+2)x-1

根据二次函数已有的n次迭代式知：

其中

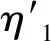
且α(B，C)=B+C+2，β(B，C)=B+2。

最后由fn(x)=h-1∘gn∘h(x)可求得fn(x)。

式(7)的n次迭代的证明与式(6)类似。首先取桥函数h(x)=1/(x-1)，则h-1(x)=1/x+1，由共轭相似得

g(x)=h∘f∘h-1(x)=(A+B+1)x2+(2A+B+2)x+A

再根据二次函数已有的结论知：

其中

且μ(A，B)=A+B+1，ν(A，B)=2A+B+2。

最后由fn(x)=h-1∘gn∘h(x)可得fn(x)。

定理3 若a1b1c1≠0且满足a1=a2+1，b2=b1+2，c1=c2+1时， 二次分式函数如式(1)所示可转化为

其中A+B+C≠-2， 它的n次迭代式为

其中

η5(φ(A，B，C)，φ(A，B，C))=

η6(φ(A，B，C)，φ(A，B，C))=

且φ(A，B，C)=A+B+C+2，φ(A，B，C)=2A+B+2。

证明取桥函数h(x)=1/(x-1)， 则h-1(x)=1/x+1， 由共轭相似得

g(x)=h-1∘f∘h(x)=(A+B+2)x2+(2A+B+2)x+A

再根据二次函数已有的n次迭代式的结论知：

其中

且φ(A，B，C)=A+B+C+2，φ(A，B，C)=2A+B+2。

最后由fn(x)=h-1∘gn∘h(x)可得fn(x)。

2 结束语