完全二部图K8，n(3 975≤n≤7 769)的点可区别E-全染色

杨 澜，陈祥恩

(西北师范大学数学与统计学院，甘肃 兰州 730070)

1 预备知识

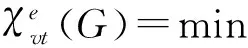
文献[5]探讨了完全图，完全二部图K2，n、星、轮、扇、路和圈的VDET染色.文献[6]得出了mC3和mC4的VDET色数.文献[7-9]中讨论了完全二部图K3，n，K4，n，K5，n的VDET染色.文献[10]讨论了完全二部图K7，n的VDET染色.本文主要讨论K8，n(3 975≤n≤7 769)的VDET染色并得到了K8，n的VDET色数.

本文中，令V(K8，n)=X∪Y，E(K8，n)={uivj|1≤i≤8，1≤j≤n}，其中

X={u1，u2，…，u8}，Y={v1，v2，…，vn}.

给定图G的一个E-全染色，规定以下记号：

C(X)={C(u1)，C(u2)，…，C(u8)}，C(Y)={C(v1)，C(v2)，…，C(vn)}.

2 主要结果及其证明

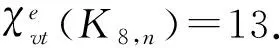
证明先证K8，n不存在12-VDET染色.假设K8，n有1个12-VDET染色f，所用颜色分别为1，2，3，4，5，6，7，8，9，10，11，12.考虑以下3种情形：

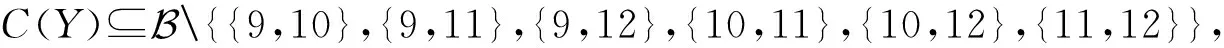
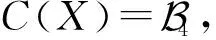
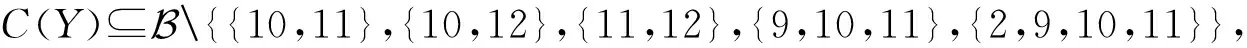
(ⅰ) {1，10，11}，{1，10，12}，{1，11，12}都是Y中某些顶点的色集合，则X中每个颜色为1的点的色集合至少同时包含10，11，12中的2种色，不妨设为10和11.

a.若{2，10，11}，{2，10，12}，{2，11，12}都是Y中某些顶点的色集合，则X中每个颜色为2的点的色集合至少同时包含10，11，12中的2种色，不妨设为a和b，且a，b∈{10，11，12}.由于{10，11}∩{a，b}≠∅，因此X中每个顶点的色集合同时包含10，11中的至少1种色，与假设矛盾.

b.若{2，10，11}，{2，10，12}，{2，11，12}中恰有2个或1个是Y中某些顶点的色集合，则X中每个颜色为2的点的色集合至少同时包含10，11，12中的1种色，不妨设为a，且a∈{10，11，12}.由于{10，11}∩{a}=∅，因此a=12.此时只有以下集合可以作为X中顶点的色集合：{1，2，3，4，5，6，7，8，9，10，11}，{1，2，3，4，5，6，7，8，9，10，11，12}，{1，2，3，4，5，6，7，8，9，12}，{1，2，3，4，5，6，7，8，9，10，12}，{1，2，3，4，5，6，7，8，9，11，12}.5个集合不能区分X中的8个顶点，矛盾.

(ⅱ) {1，10，11}，{1，10，12}，{1，11，12}中恰有2个或1个是Y中某些顶点的色集合，则X中每个颜色为1的点的色集合至少同时包含10，11，12中的1种色，不妨设为10.此时{2，10，11}，{2，10，12}，{2，11，12}中至多有2个不是Y中某些顶点的色集合.

a.若{2，10，11}，{2，10，12}，{2，11，12}都是Y中某些顶点的色集合，则X中每个颜色为2的点的色集合至少同时包含10，11，12中的2种色，不妨设为a和b，且a，b∈{10，11，12}.由于{10}∩{a，b}=∅，故{a，b}={11，12}，此时只有以下集合可以作为X中顶点的色集合：{1，2，3，4，5，6，7，8，9，10}，{1，2，3，4，5，6，7，8，9，10，11}，{1，2，3，4，5，6，7，8，9，10，12}，{1，2，3，4，5，6，7，8，9，10，11，12}，{1，2，3，4，5，6，7，8，9，11，12}.5个集合不能区分X中的8个顶点，矛盾.

b.若{2，10，11}，{2，10，12}，{2，11，12}中恰有2个或1个是Y中某些顶点的色集合，则X中每个颜色为2的点的色集合至少包含10，11，12中的1种色，不妨设为a，且a∈{10，11，12}.由于{10}∩{a}=∅，否则X中每个顶点的色集合同时包含颜色10，与假设矛盾，因此a=11或a=12.不妨设前者成立，此时只有以下集合可以作为X中顶点的色集合：{1，2，3，4，5，6，7，8，9，10}，{1，2，3，4，5，6，7，8，9，10，11}，{1，2，3，4，5，6，7，8，9，10，12}，{1，2，3，4，5，6，7，8，9，10，11，12}，{1，2，3，4，5，6，7，8，9，11}，{1，2，3，4，5，6，7，9，11，12}.6个集合不能区分X中的8个顶点，矛盾.

(ⅲ) {1，10，11}，{1，10，12}，{1，11，12}均不是Y中任一顶点的色集合，即

则

有8+n≤3 983-8+7，可得n≤3 984，矛盾.

情形2.3 当X中每个顶点的色集合至少同时包含3，4，…，12中的8种色，不妨设为3，4，5，6，7，8，9，10，此时只有以下集合可以作为X中顶点的色集合：{1，2，3，4，5，6，7，8，9，10}，{1，2，3，4，5，6，7，8，9，10，11}，{1，2，3，4，5，6，7，8，9，10，12}，{1，2，3，4，5，6，7，8，9，10，11，12}.4个集合不能区分X中的8个顶点，矛盾.

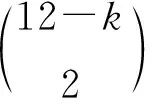
故当3 975≤n≤7 769时，矛盾.

首先，确定X中顶点的色集合，以及X中每个顶点的颜色.令：

C(u1)={1，2，6，7，8，9，10，11，12，13}，f(u1)=2；

C(u2)={1，2，3，6，7，8，9，10，11，12，13}，f(u2)=2；

C(u3)={1，2，4，6，7，8，9，10，11，12，13}，f(u3)=2；

C(u4)={1，2，5，6，7，8，9，10，11，12，13}，f(u4)=2；

C(u5)={1，2，3，4，6，7，8，9，10，11，12，13}，f(u5)=2；

C(u6)={1，2，3，5，6，7，8，9，10，11，12，13}，f(u6)=2；

C(u7)={1，2，4，5，6，7，8，9，10，11，12，13}，f(u7)=1；

C(u8)={1，2，3，4，5，6，7，8，9，10，11，12，13}，f(u8)=1.

其次，确定Y中顶点的色集合.让顶点v1，v2，…，v7 769分别对应下列色集合：含颜色{3，4，5，6，7，8，9，10，11，12，13}的2-子集但不是{3，4}，{3，5}，{4，5}；含颜色{1，2，3，4，5，6，7，8，9，10，11，12，13}的3-子集、4-子集、5-子集、6-子集、7-子集、8-子集、9-子集，但不是{2，3，4}，{2，3，5}，{2，4，5}，{3，4，5}，{2，3，4，5}.

顶点vj(1≤j≤7 769)和它的关联边u1vj，u2vj，…，u8vj的具体染色方案在表1中给出.

表1 K8，7 769的顶点vj(1≤j≤7 769)及其关联边的染色方案