基于RFE-RF-XGBoost的坝体位移预测研究
王昕宇,杨 鹏,2,戴健非
(1.北京联合大学北京市信息服务工程重点实验室,北京 100101;2.北京科技大学土木与资源工程学院,北京 100083)
0 引言
尾矿库是选择有利地形筑坝拦截谷口或围地形成的具有一定容积、用以贮藏尾矿和尾矿澄清水的专用场地,是一种高势能的人造泥石流危险源[1].尾矿坝是使尾矿库形成一定容积,便于尾矿矿浆能堆存其中的一种由尾矿堆积碾压而成的坝体,尾矿坝一旦溃坝,会严重威胁下游居民的生命安全,污染下游区域环境,造成大量经济财产损失.其安全稳定对矿山生产、安全、环境保护至关重要[2].目前,自动化系统虽然能够对尾矿坝主要指标进行监测,但安全监测仅是初步,能够根据以往监测数据建立预测模型,了解其形变规律才是最重要的.因此,将尾矿坝坝体位移数据与数学模型相结合实现预测预警,对尾矿库的安全稳定管理具有重要意义[3].
我国对于尾矿坝坝体位移预测起步相对较晚,借鉴了大量的大坝(水坝、堆石坝等)位移预测体系方法.目前国内外研究者围绕坝体位移预测模型展开大量的研究,其中黄定川等[4]根据尾矿库初期坝沉降数据为例构建BP神经网络预测模型,重点研究其拓扑和学习算法;胡军等[5]提出使用基于结构风险最小化的SVM算法进行预测学习,并通过种族鱼群优化算法优化参数;李丰旭等[6]针对形变模型发生早熟、预测不稳定的现象,引入基于混沌搜索的多种群遗传算法,改进遗传参数的计算方式;甄明秀[7]以白岩尾矿坝为媒介,比较回归模型、时序模型、灰色模型在形变预测中的适应能力;贾龙等[8]针对verhulst模型预测精度不足的问题,使用三类弱化缓冲算子处理数据,重新构建verhulst模型;钟登华等[9]提出了基于自适应网络模糊推理系统优化的灰色模型;文献[10]提出了一种新的分布式时间序列演化预测方法,将变形预测的思想与结构化方法相结合,提高了变形预测的可靠性;文献[11]针对回归模型中拟合残差序列的混沌特性,采用多尺度小波分析对残差序列进行分解和重构,构建BP神经网络模型.
上述研究对坝体的安全稳定管理有着重要意义,但并未充分涉及外部因素对形变的影响,仅考虑位移变化的时效性.合理的特征选择能够提升模型精度,降低时间复杂度.因此,本文提出建立特征递归消除(Recursive Feature Elimination,RFE)和随机森林(Random Forest,RF)、极限梯度提升(Extreme Gradient Boosting,XGBoost)相融合的预测模型,并与BP神经网络、LSTM神经网络等模型进行了对比.本文对防止溃坝事故和矿山安全管理具有一定参考价值.
1 坝体位移模型构建
1.1 随机森林
随机森林是Cutler与Breiman于2001年提出的一种统计学习方法[12].RF是根据一定准则生成一定数量的决策树并进行组合,在训练决策树的过程中随机选择特征以提高模型预测精度.可用于模拟多重非线性关系,该算法的实现步骤如下:
(1) 对含有m个样本的数据集,使用自助法从数据集中随机有放回的选取m个样本.经过N次选取,产生N个bootstrap样本集,对N个样本集训练构成N个回归树,而每次选取后的剩余样本全部放入N个袋外数据(OBB)作为测试样本.
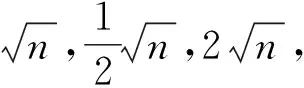
(3) 每个回归树自上往下递归分支,设定随机森林中回归树的个数作为回归树生长的停止条件.
(4) 综合N个回归树并取其平均值构成随机森林回归模型,公式为
(1)
式中:f(x)表示随机森林模型,Tj(x)是单个回归树模型,j=1,2,…,N,使用OBB中的样本作为测试集并根据回归分析的相关评估指标来判断模型的预测效果.
自助法是一种非参数统计方法,也被称作bootstrap,其基本步骤如下:
(1) 从样本中抽取一定量样本,允许重复抽样(抽取数量自拟).
(2) 统计抽取的样本以计算待估计统计量M.
(3) 重复抽取N次,计算N个统计量M.
(4) 根据N个统计量M的方差估计统计量M的方差.
1.2 特征递归消除
特征递归消除是一种基于wrapper包裹型模式下的后向搜索算法,常用于特征选择[13].相较于filter型算法,wrapper将特征选择问题转化为特征子集搜索问题,筛选多个特征子集,使用一个机器学习模型评估效果,重复该过程直至产生最优的特征子集,RFE算法是在该方法基础上的简化,基本步骤如下:
(1) 选择全部特征并构造初始特征集.
(2) 在特征集上训练一个机器学习模型,本文采用随机森林算法构建回归模型.
(3) 依据平均不纯度的减少程度评估各特征的重要性,并由高到低排列.回归树模型以方差或最小二乘法作为不纯度条件,公式为:
(2)
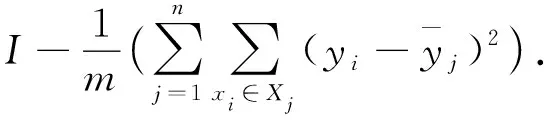
(3)

(4) 剔除重要性最低的特征,构造新的特征集.
(5) 重复步骤2到步骤4,直到特征集没有进一步的特征可供保持,特征被剔除的顺序是特征选择的依据,越早被剔除的特征越应舍弃,越晚被剔除的特征越应保留.
1.3 极限梯度提升
极限梯度提升是陈天奇博士于2016年提出的一种集成学习方法,以CART回归树和随机森林为基础的一种扩展延伸,属于Boosting方法中的一种提升算法[14].Boosting是将多个弱学习器提升为强学习器的一种方法,先训练第1个弱学习器,根据弱学习器的误差表现改变训练样本权重,使训练误差大的样本受到更多的关注.将改变权重的训练样本导入第2个弱学习器,再根据训练误差调整权重,如此反复,直到弱学习器的数量达到某一指定值n,将n个弱学习器整合为强学习器.XGBoost在Boosting的基础上使用增量学习并增加L1和L2正则化项,提升泛化能力,减小过拟合,基本算法如下:
(4)
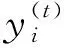
目标函数为
(5)
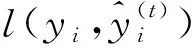
1.4 RFE-RF-XGBoost预测模型构建
RFE-RF-XGBoot预测模型构建流程如下:
(1) 数据集整理,删除缺失值,数据做最小-最大标准化(Min-Max Normalization)处理.
(2) 坝体垂直沉降作为输出,其余特征作为输入,导入RFE-RF模型进行特征选择.
(3) 按特征重要度重建数据集,采用留出法交叉验证(Holdout Cross Validation),将数据依照时间顺序划分为训练集(60%)、验证集(20%)、测试集(20%).
(4) 设定XGBoost模型的初始参数对训练集拟合,利用验证集计算误差指标并配合网格搜索与模型历史最优指标对比.
(5) 若模型预测精度提高,则当前指标为新的历史最优指标,继续调整参数,以此反复.反之,若模型预测精度低于历史最优指标,则说明模型出现过拟合现象,停止调整参数.
(6) 测试样本导入模型计算预测误差,查看模型预测效果.基本流程如图1所示.
1.5 模型评估指标
本文使用平均绝对误差(Mean Absolute Error,MAE)和相对误差(Relative Error,RE)作为模型的评估指标,MAE也被称作平均绝对离差即绝对误差的平均值,是参数估计值与参数真值之差绝对值的期望值.MAE可以评价模型预测的绝对准确度,MAE的值越小,说明预测模型描述整体实验数据具有更好的精确度,模型更稳定[16].其公式为
(6)

相对误差RE是指被测量的真实值与预测值的绝对误差与被测量真实值之比乘以100%所得的数值,以百分数表示.其公式为
(7)
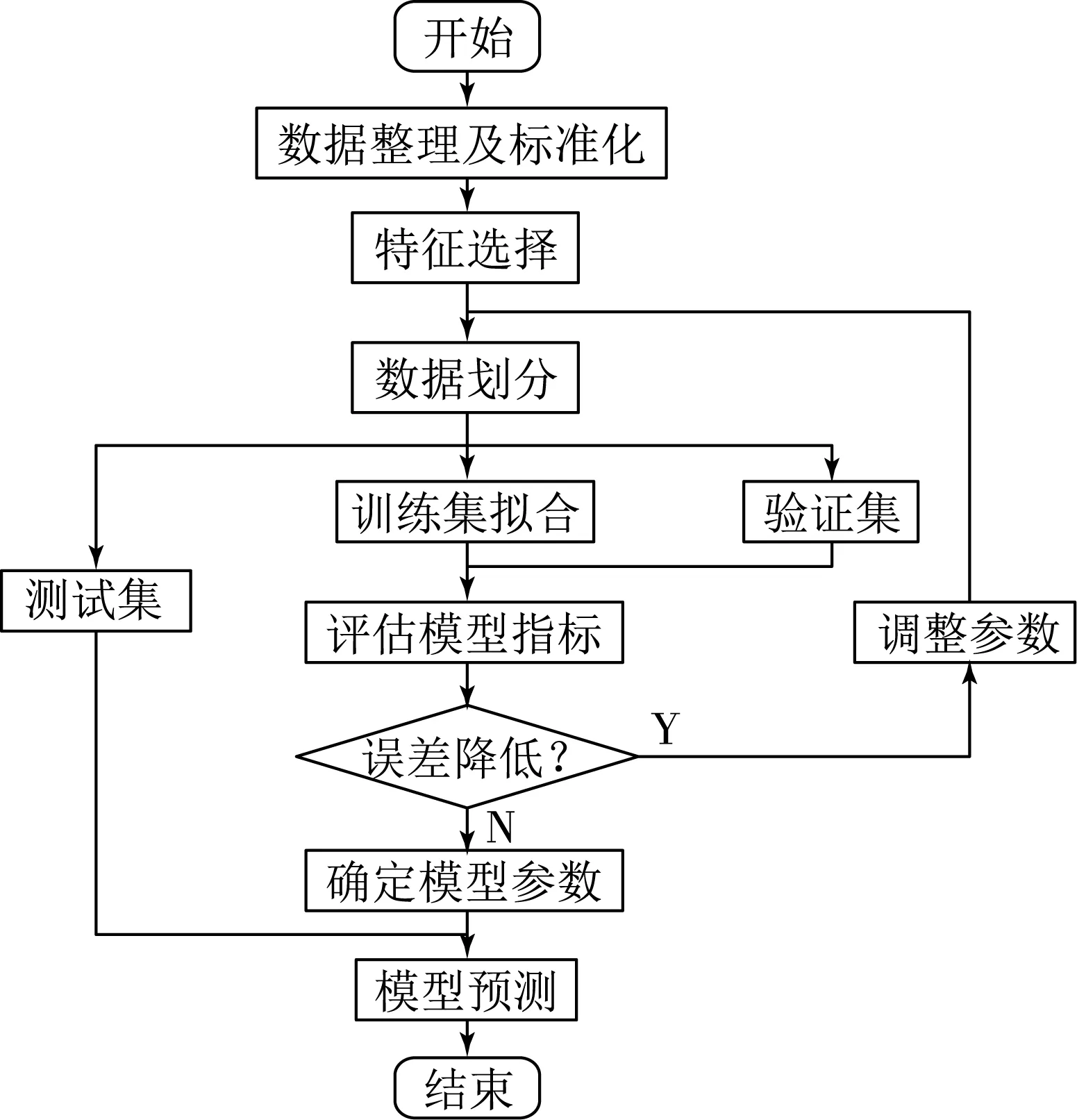
图1 RFE-RF-XGBoost模型构建流程
2 实例应用
2.1 数据来源
本文采用某尾矿库安全监测系统采集的2017年11月至2019年8月共7 000条实时数据进行预测实验.该尾矿库规划用地面积约1.76 km2.尾矿库区汇水面积3.91 km2,属于二级尾矿库,尾矿库初期坝属透水堆石坝,初期坝设计标高为450.00 m,高度约35 m,最终堆积标高为647.00 m.尾矿堆积坝采用上游式堆筑法,即平行初期坝轴方向外尾矿库内逐级填筑堆积坝,增加库容排放尾矿.尾矿堆积坝每级高度2 m,内外坡比1∶2∶5,顶宽2 m,堆积坝总高度为197 m.特征包括3个监测点处的浸润线埋深(JRX1-1、JRX1-2、JRX1-3)、库水位高度(KSW)、降雨量(RAIN)、坝体表面平行坝轴线位移(BMWY-X)、垂直坝轴线位移(BMWY-Y)、垂直沉降(BMWY-Z),部分样本特征数据如表1所示.
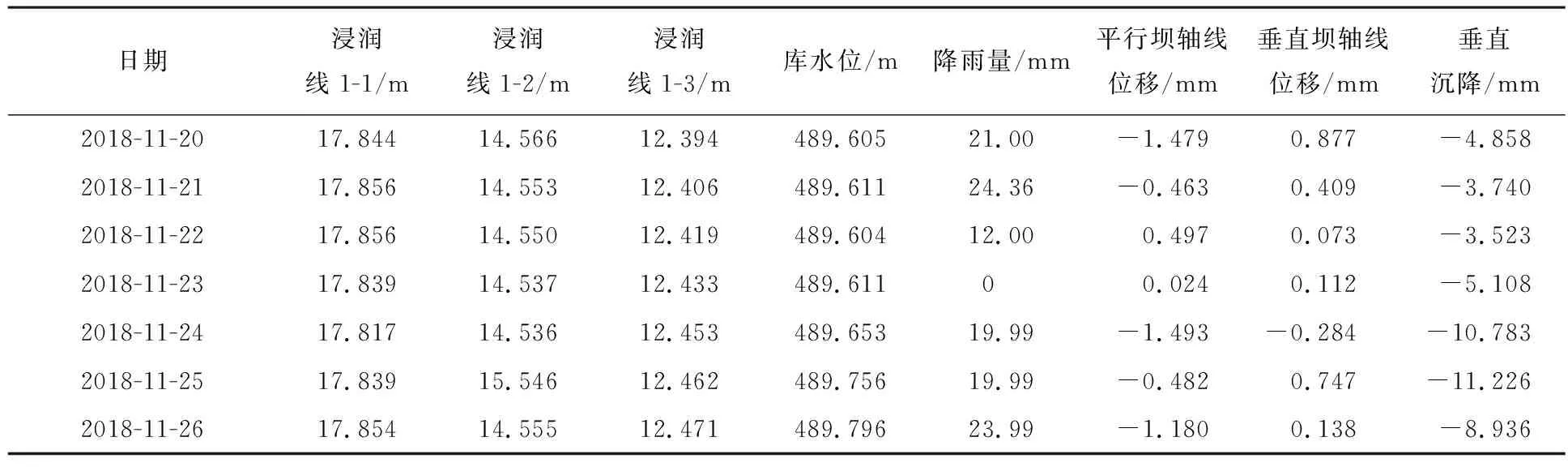
表1 部分实验样本特征
2.2 特征选择
凭借PyCharm搭配Anaconda开源包、环境管理器,利用python3语言编写.以3点浸润线埋深、库水位高度、降雨量、坝体表面平行坝轴线位移、垂直坝轴线位移作为输入,坝体垂直沉降作为输出.首先调用preprocessing模块的scale函数对输入输出特征进行快速Min-Max标准化,然后导入ensemble模块中的RandomForestRegressor函数,默认决策树数值为100并拟合数据,计算输入特征重要性.结果表明库水位重要性占比为0.399,其次为两点浸润线埋深,分别占0.184和0.176.坝体表面平行坝轴线位移、垂直坝轴线位移分别占0.065和0.092.降雨量占比最低,为0.020,第一次筛选结果如图2所示.

图2 第一次特征筛选
待剔除降雨量特征后,数据重新导入模型并计算重要性,重要性占比发生变化:浸润线埋深1-2和1-3占比降低,分别为0.063和0.173,第二次筛选结果如图3所示.
经多次筛选,重要性排名从高到低依次是库水位、浸润线埋深1-1、浸润线埋深1-3、垂直坝轴线位移、平行坝轴线位移、浸润线埋深1-2、降雨量.其中库水位重要性最高,通过mic函数计算相关性为0.530,表明库水位与垂直沉降具有强非线性相关性.本文选择浸润线埋深1-1、浸润线埋深1-3、库水位、垂直沉降、降雨量为特征重建新数据集,为预测t时刻的垂直沉降,以t-dt时刻的浸润线埋深、库水位、垂直沉降、降雨量为输入,其中dt为1,2,3 d,新数据集部分样本如表2所示,通过特征选择可有效减少预测过程中的特征冗余,避免特征间的负面影响.
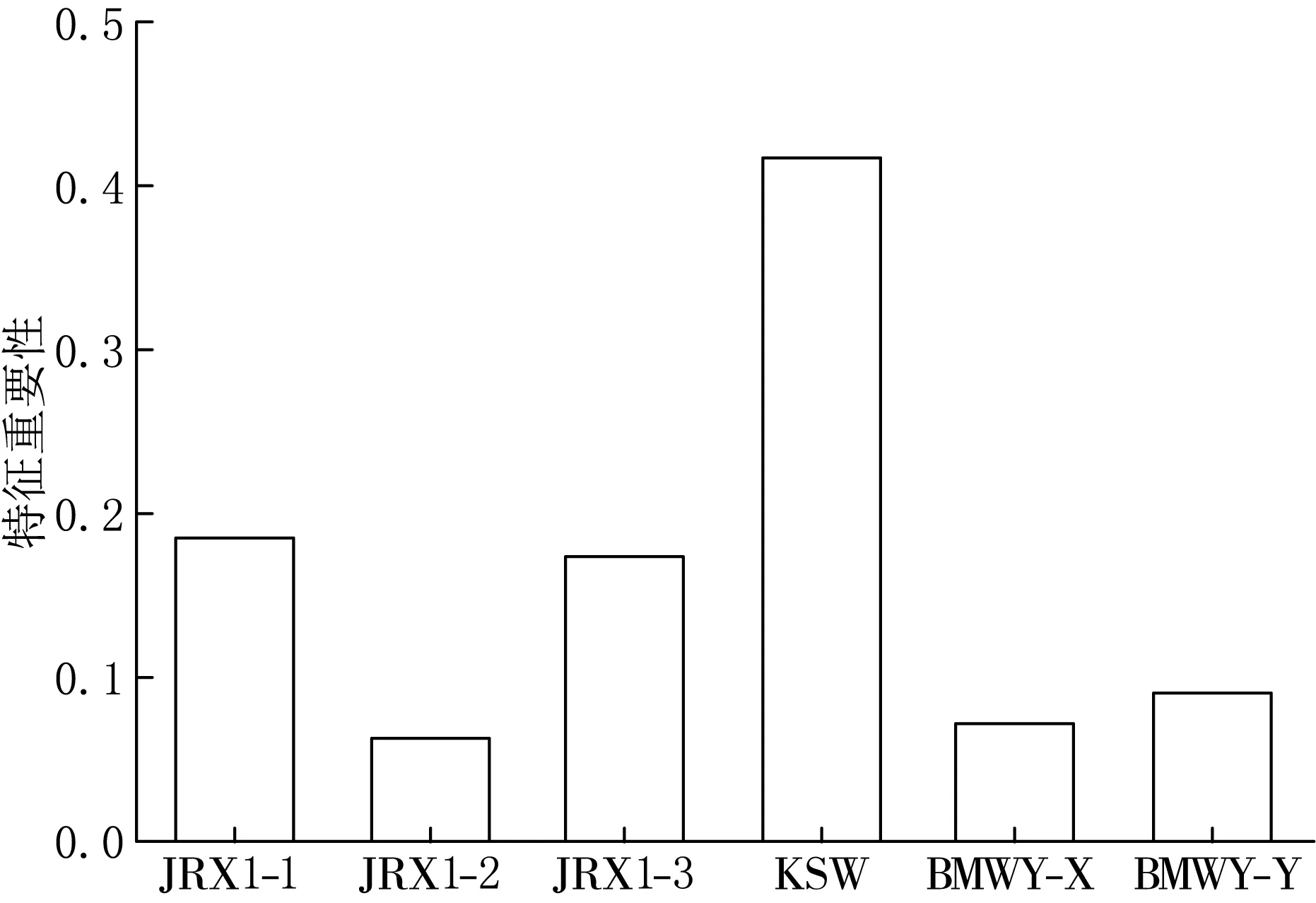
图3 第二次特征筛选
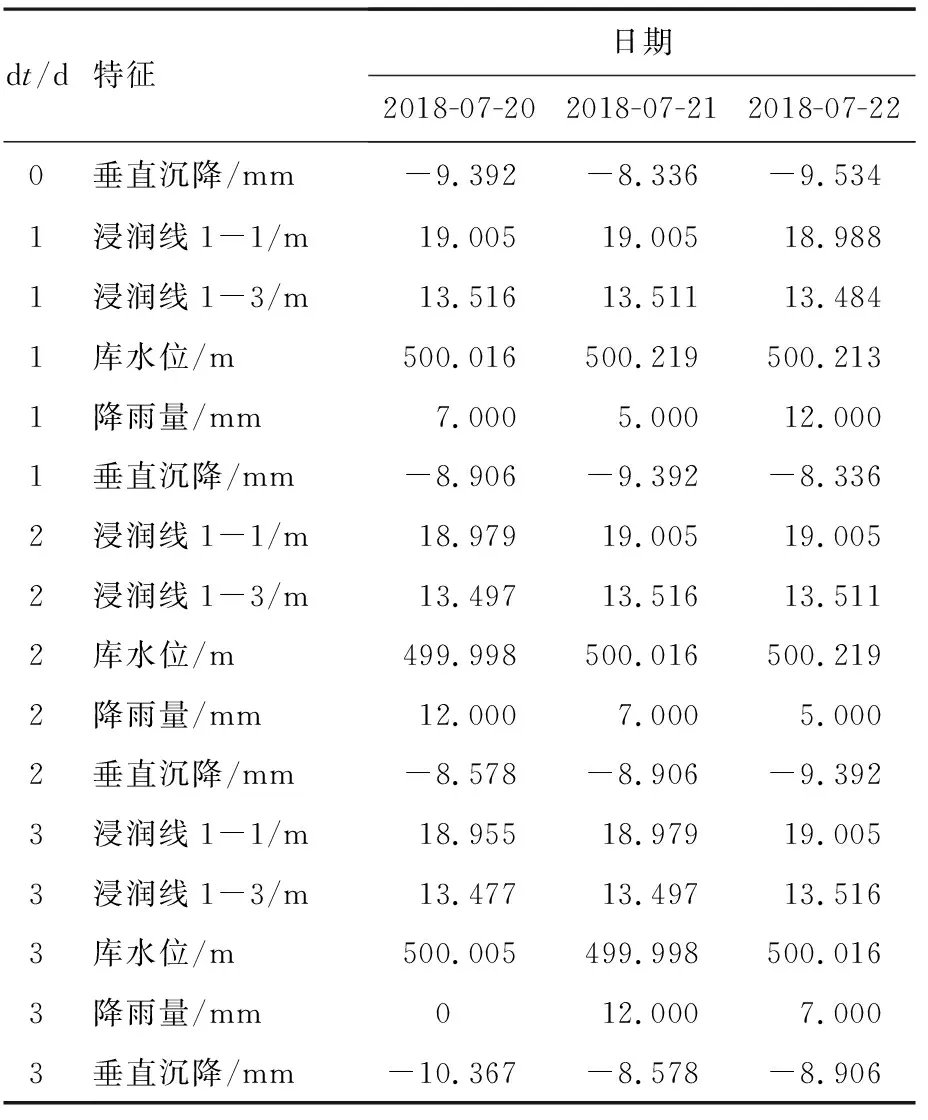
表2 新数据集部分样本特征
2.3 RFE-RF-XGBoost模型建立
根据RFE-RF特征选择排列重建新数据集后,数据集采用留出法交叉验证,依照时间顺序划分为训练集(60%)、验证集(20%)、测试集(20%),其中训练集导入XGBoost框架的XGBRegressor函数中训练拟合,验证集为模型泛化能力验证指标,测试集用于检验模型预测效果.XGBoost模型参数主要包括:回归树数量(n_estimators)、回归树最大深度(max_depth)、回归树最小叶子节点样本权重和(min_child_weight)、损失函数减小阈值(gamma)、回归树随机采样率(subsample)、回归树特征采样率(colsample_bytree)、L1正则化权重(reg_alpha)、L2正则化权重(reg_lambda)、学习率(learning_rate).本文根据验证集预测指标,配合网格搜索方法逐步调整模型参数,过程如下:
(1) 调整回归树数量,n_estimators从[10,300]之间取值计算验证集误差指标,结果如图4所示.[10,40]区间内误差曲线呈下降趋势,当n_estimators=40时,误差最小,MAE=0.072,[50,100]区间内误差曲线逐渐增高,泛化能力降低.
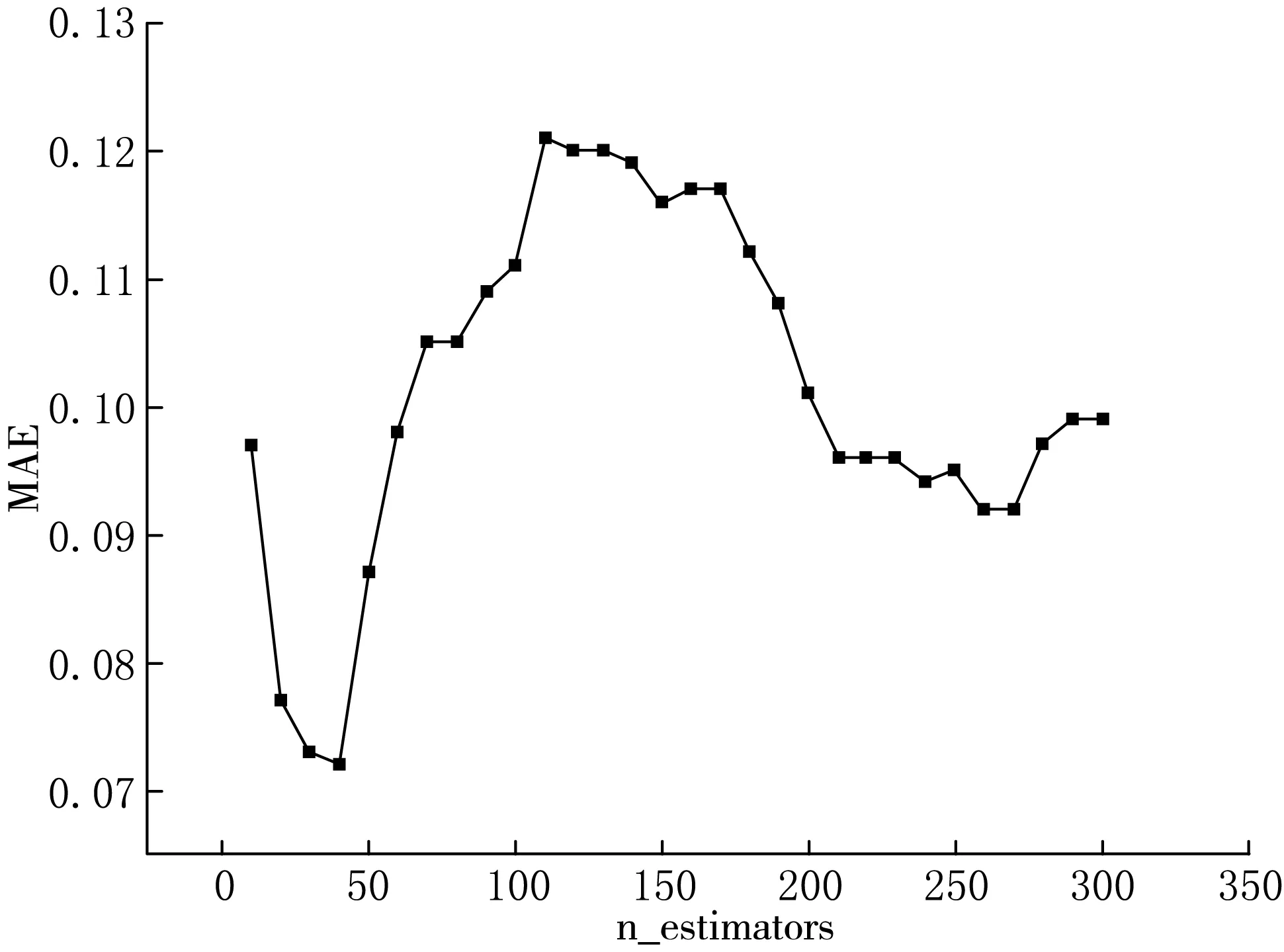
图4 回归树数量对MAE的影响
(2) 调整回归树最大深度和最小叶子节点样本权重和,max_depth调整区间为[0,10],min_child_weight调整区间为[0,20],结果如图5所示.max_depth=6,min_child_weight=19时,误差最小,MAE=0.068.
(3) 调整损失函数减小阈值,gamma调整区间为[0,1],gamma=0.05时,误差最小,MAE=0.067.
(4) 调整回归树随机采样率和回归树特征采样率,subsample和colsample_bytree调整区间为[0,1],subsample=0.5,colsample_bytree=0.9时,误差最小,MAE=0.065.

图5 回归树最大深度与最小叶子节点
(5) 调整L1正则化权重和L2正则化权重,reg_alpha和reg_lambda调整区间为[0,7],reg_alpha=0.06,reg_lambda=0.1时,误差最小,MAE=0.062.
(6) 调整学习率,learning_rate调整区间为[0,1],learning_rate=0.2时,误差最小,MAE=0.059.
经多轮参数调整,最小平均绝对误差MAE=0.059.表3为验证集的10组样本预测结果和相对误差,可知垂直沉降预测最大相对误差为7.21%,最小相对误差为0.17%.
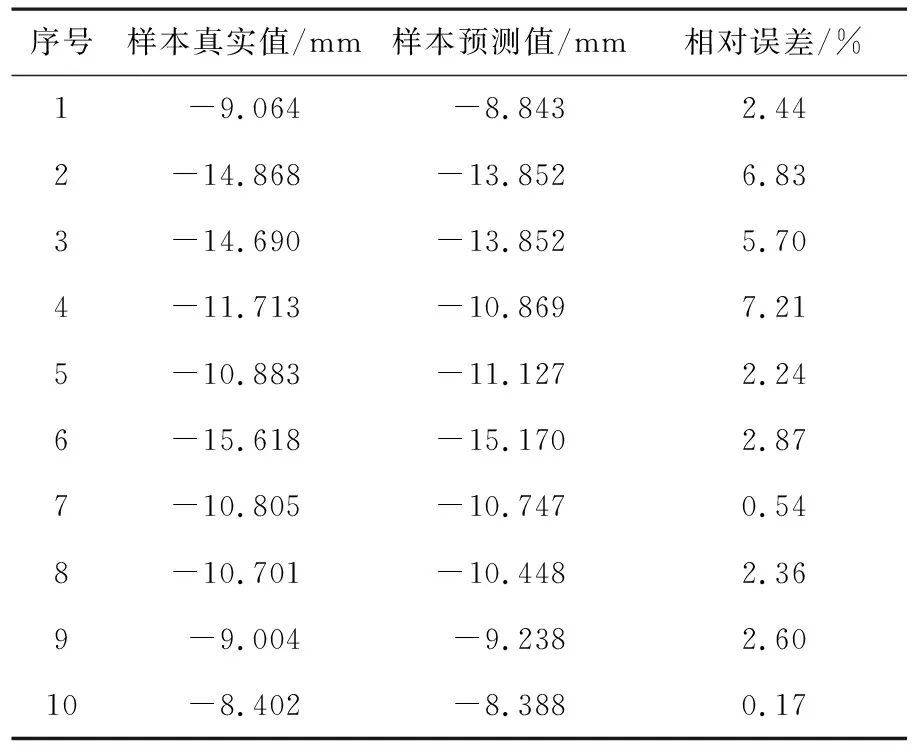
表3 RFE-RF-XGBoost对验证集样本预测结果
2.4 不同方法预测结果比较
本文使用tesorflow神经网络框架对BP神经网络编写及测试,网络结构包括输入层、隐藏层、输出层.其中隐藏层激活函数为tanh函数,输出层激活函数为线性函数.输入层神经单元数为24,坝体表面垂直沉降为输出,输出单元个数为1.使用SGD优化器实现权重、阈值更新.学习率为0.01,Dropout为0.2,迭代3 000次.BP神经网络的隐藏层神经元个数一般是根据以往经验和反复的试验选取,为寻找预测效果最好的网络结构,本文通过Kolmogorov定理计算隐含层神经元个数,公式为
h=2m+1.
(8)
其中:m为输入层神经元个数,h为隐含层神经元个数,网络结构为24-49-1时,预测误差MAE=0.133.
作为传统深度学习模型代表之一,LSTM神经网络模型通过keras深度学习框架搭建,网络结构包括输入层、LSTM层、全连接层、输出层[18].输入层神经元24个,LSTM层神经元60个,输出层神经元1个.LSTM层激活函数为tanh,输出层激活函数为线性函数.优化器是Adam,学习率为0.01.Dropout=0.2,batch size=64,epochs=46时,预测误差MAE=0.078.SVR预测模型通过sklearn模块的SVR函数构建,算法使用高斯核函数,正则化系数为0.8时,MAE=0.080[19].图6与表4为RFE-RF-XGBoost、XGBoost、LSTM神经网络、BP神经网络、SVR预测结果对比.

表4 多方法预测结果
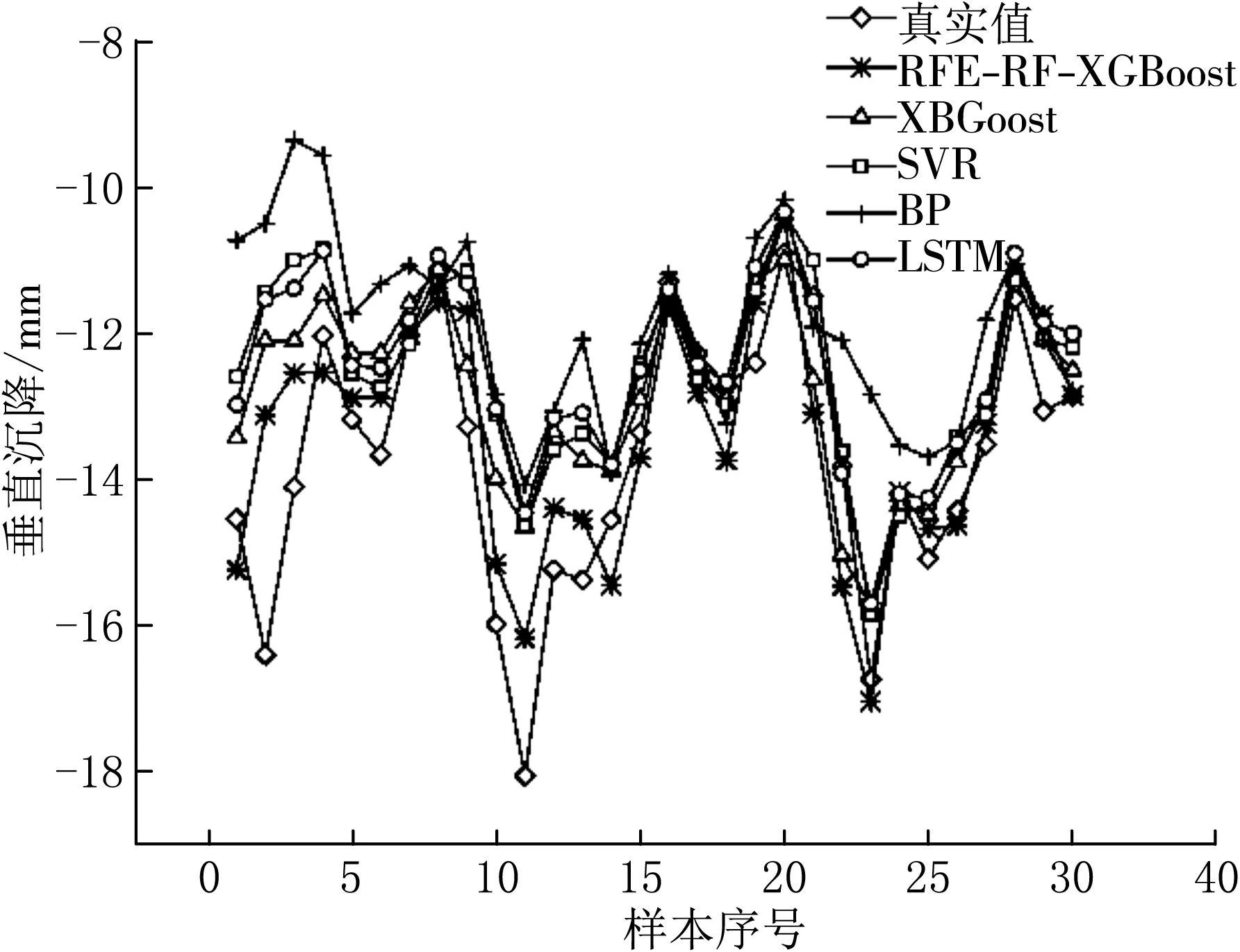
图6 多方法预测结果对比
表4为各模型样本预测结果和相对误差,由表4可知:RFE-RF-XGBoost模型最小相对误差为1.01%,最大相对误差为6.79%.XGBoost模型最小相对误差为3.02%,最大相对误差为12.84%.各模型MAE依次为0.060,0.062,0.080,0.133,0.078,平均相对误差分别为3.60%,7.53%,11.20%,16.76%,9.25%,其中RFE-RF-XGBoost预测效果最好,平均相对误差低于XGBoost3.93%.
3 结论
本文以某尾矿库2017年11月至2019年8月的历史数据为实验样本,提出使用随机森林配合特征递归消除与极限梯度提升模型相融合.实验结果表明:库水位与垂直沉降重要性最高,非线性相关性为0.530.RFE-RF-XGBoost对比XGBoost模型平均绝对误差降低了0.2%,平均相对误差降低了3.93%.所提出模型能够提高坝体位移的预测精度,总体精度高于XGBoost模型、SVR模型、BP神经网络、LSTM神经网络.借助RFE-RF-XGBoost预测模型,矿山管理部门可依据预测结果及早实施相应安全措施,对于矿山施工决策、安全管理,减少溃坝事故具有参考意义.

