考虑基地住宿问题的高铁列车乘务排班计划编制

李 雯，代存杰，巨玉祥，成 洋，张芳英

(1. 兰州交通大学 交通运输学院，兰州 730070；2. 中国铁路兰州局集团有限公司 兰州车站，兰州 730000；3. 中国铁路兰州局集团有限公司 兰州客运段，兰州 730000)

列车乘务排班计划，是指对列车乘务班组的休息、值乘，乘务车间做出的具体规划安排，主要在列车乘务计划编制的第二个阶段完成.完善的乘务排班计划，能够减少运营成本，并对乘务员的休息、工作时间进行科学有效地安排，提升乘务员对工作的满意度，具有关键的实践价值与作用.因乘务员的组织模式、乘务车间管辖的值乘区段存在差别，所以乘务排班计划的编制同样也呈现出不一样的模式.既有研究表明，乘务排班通常选取两类方式，即固定周期和单循环两种.目前相关的研究成果有：

文献[1]研究上海市轨道交通乘务排班优化问题，将乘务工作分为日班和夜班两部分并归结为一个二分双向匹配问题，采用匈牙利算法进行求解.文献[2]应用蚁群算法，针对高速铁路单循环模式乘务排班计划编制问题，以乘务交路接续时间最短和冗余时间分布最均衡为目标进行问题求解.文献[3]将动车组交路计划的编制问题转化为多旅行商问题，采用信息素增强的蚁群算法求解，并通过现场采集的数据验证算法的有效性.文献[4]构建了乘务人员数量最少与工作时间适应的双目标模型，基于南京—常州区间的列车运行数据，使用改进的蚁群算法进行实例验证.文献[5]通过分析车次、交路及乘务员之间的关系，以乘务班组费用最小化为目标，以交路和乘务工时为约束建立优化模型，设计遗传算法进行求解.文献[6]同样将铁路乘务排班问题抽象为多旅行商问题，以排班周期最短、乘务交路间冗余接续时间分布最均衡为优化目标，构建数学优化模型，使用一种启发式修正蚁群算法进行模型求解，并以广深城际铁路为案例验证算法的有效性.文献[7]设计了引入文化基因算法的非支配遗传算法(non dominated sorting genetic algorithm-II，NSGA-II)来解决多目标作业车间调度问题，该算法增加了基于模拟退火算法的局部搜索程序.文献[8]基于时空网络模型，对于在某个责任范围内，针对使用乘务班组人数的下限展开求解.文献[9]设计自适应遗传算法，初始值为难以获取的乘务组数的最小值，所借助的遗传算法当中的染色体长度，能够在迭代中进行自适应改变.文献[10]设计的遗传算法，含有嵌入式模糊逻辑处理器，用以促使算法交叉、变异机率的增加.文献[11-12]分别研究手术调度和项目调度的相关问题，优化与完善NSGA-II算法，同时借助运算数据，由分布性以及收敛性，验证优化方式的效果.文献[13]建立了带时间窗的多车场公交乘务排班优化模型，并使用禁忌搜索算法对该问题进行求解，结果表明该方法在处理带有时间窗的多车场公交乘务组跨线排班问题时具有良好的应用效果.文献[14]研究等待折返的动车乘务交路改进及优化的问题，基于集合分解问题扩展问题模型，同时运用遗传—蚁群混合算法展开求解.文献[15]针对公交线路多目标优化模型，采用改进的NSGA-II算法，以自然数进行编码，采取锦标赛选择策略进行选择操作，并采用均匀变异的方式，得到了较好的求解结果.

在已有文献中，通常将最小化班组数量，劳动均衡性做为求解目标，却没有对乘务班组因值乘不同出发时刻、到达时刻交路而产生的住宿问题进行优化.本文针对乘务基地住宿问题进行了讨论，并设计了相应的优化求解方法，在客运段车队(间)实际工作中，有较强现实意义.

1 乘务排班计划多目标数学模型

1.1 问题描述

本文讨论的列车乘务排班计划是指，在指定周期排班模式[2]下，对周期内乘务班组与值乘交路的匹配关系做出具体的安排.客运段通常以运营成本最小作为乘务计划编制的总体目标，其中人员成本和住宿成本在运营成本中占比最高.考虑到工作实际中，因值乘早发交路、晚至交路在乘务基地的住宿成本取决于在基地住宿的乘务班组数量，因此将班组数量和基地住宿班组数目作为乘务排班计划数学模型中的优化目标.又因各班组完成的任务量应当是均衡的，劳动均衡性也作为求解的目标之一.

基于以上分析，在模型构建过程中，在将最小化乘务班组数量、劳动均衡性作为目标的基础上，首次将最小化基地住宿乘务组数目作为求解目标，在已有研究基础上，将乘务交路与乘务班组的指派关系和周期内的劳动时长限制作为模型约束，对该问题进行优化.

1.2 指定周期乘务排班计划指派模型

综上分析，在原有研究[5]的基础上将乘务排班计划编制问题看作经典的指派问题，在此基础上建立多目标优化模型.模型中的符号定义如表1所列.

表1 模型符号定义Tab.1 Definition of model symbols

具体数学模型如下:

(1)

minZ2=

(2)

目标函数(1)为乘务班组数量的最小值.目标函数(2)为各乘务班组劳动时长差值最小.

(3)

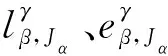
(4)

(5)

式(4)和式(5)为实际工作中乘务交路和乘务班组的一一对应要求，即每天乘务班组只能值乘一个乘务交路，且一个乘务交路只能由一个乘务班组值乘.

(6)

式(6)为给定乘务排班周期范围内的工作时长约束，月度工时限制为166.6 h.

2 改进的NSGA-II算法求解列车乘务排班计划

乘务排班计划编制问题数学模型为多目标优化模型，该类问题中的每个子目标间一般是相互矛盾的，求得的解被称之为非支配解或Pareto最优解，主要特征为优化任一目标函数的同时，并不影响至少一个其他目标函数.

结合该问题特点，设计基于实数编码的NSGA-II算法对模型进行求解，并对算法进行改进，使用基于禁忌思想的变异方式，尽可能的减少非可行解的产生.针对求解时容易出现的收敛速度慢、易陷入局部最优的问题，引入基于小生境的精英保留策略及自适应交叉变异算子的改进方式.此种改进方式符合问题的特点，可以提高算法的收敛速度，同时提高解的分布.

2.1 算法设计及改进

2.2.1 算法设计

1) 初始种群的产生

采用实数三层编码模式，第一层设指定周期内的排班计划为染色体，第二层设排班计划内每天的值乘计划为基因，第三层为某天值乘计划中乘务班组的排列次序.指定排班周期与乘务交路个数之积T×m作为初始种群中个体的乘务班组数，以实数代表一个班组出乘，其排列位置代表乘务班组值乘的交路和日期.

2) 适应度计算

适应度为遗传算法中决定个体优劣的指标，本例中，直接利用目标函数Z1、Z2、Z3数值作为个体的适应度.

3) 非支配排序

非支配排序是本算法筛选后代个体的排序方式，根据适应度函数对个体进行非劣分层，比较个体函数值的大小，将当前种群中所有非劣解划分为同一等级，令其为1；在剩余个体中找出新的非劣解，令其等级为2；重复以上过程，直至种群中所有个体都被设定相应的等级.

4) 锦标赛选择

随机选择两个个体，首先比较非劣等级，如果非劣等级不同，则取非劣等级较小的个体，若非劣等级相同，则以拥挤度CDl为标准，取拥挤度大的个体，形成新种群.

5) 交叉运算

针对问题编码特点，采用单点交叉的方法，对排班计划中某一天的值乘计划进行交叉，在具体操作中，先对染色体进行随机配对；其次随机设置交叉点位置；最后再相互交换配对排班计划的某一天的值乘计划.算法中的交叉运算如图1所示.

6) 变异运算

针对每天值乘计划中的值乘班组进行变异，在变异操作中引入禁忌思想，设置两种变异方式.首先随机选择某天乘务计划中乘务交路的基因变异位置，然后针对每天的值乘交路设置禁忌表，将当天出乘班组编号放入禁忌表中，变异选择为在当天不出乘的乘务班组.其次对值乘早晚交路做标记，值乘晚至交路的班组，判断是否在次日的禁忌表中，若不在禁忌表中，则在值乘早发交路变异为相同班组.

2.2.2 算法改进

根据已有研究[11]，计算染色体的海明距离即小生境尺寸CDl来实现拥挤密度的排序并减轻计算量，同时改善解的分布多样性.按海明距离由疏到密的标准，将个体复制到下一代，直到下一代群体规模达到进化群体规模终止复制.某非支配染色体集上第l个染色体的拥挤度CDl按下式计算:

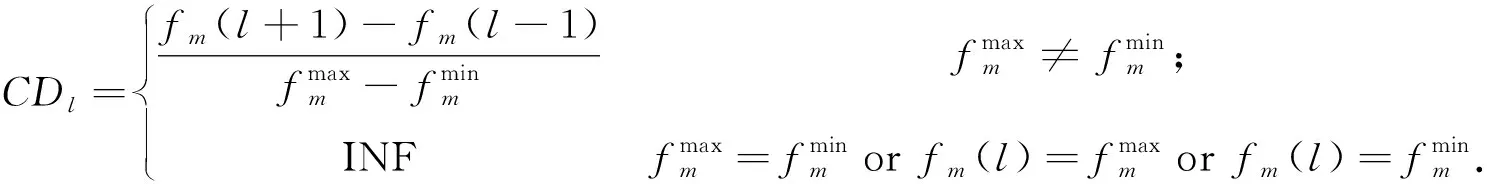
(7)

为避免NSGA-II算法因选定交叉和变异概率带来的弊端，引入概率自适应策略，动态控制遗传操作的频率.使用自适应交叉算子克服不成熟的收敛，使用自适应变异算子保持种群内个体的多样化，降低陷入局部解的可能，其中自适应交叉算子和变异算子分别为

宋榕华....................................................................................................................................................................科莱恩大中华区可持续发展及管理事务总监

(8)

(9)

算法经过多次迭代后，乘务班组数值不再有变化，并达到迭代次数时终止.

2.3 算法具体流程

步骤1设置进化代数计数器t=1,随机产生满足不超过周期内最大工作时长初始种群P(t)，设置种群中班组数量为T×m；

步骤2计算每个个体相应的目标函数值fm；

步骤3快速非支配排序.对种群P进行非劣分层，直至种群中所有个体被设定相应等级；

步骤4锦标赛选择.随机选择两个个体，若非劣等级不同，首先比较非劣等级，取级数较小的个体；若个体在同等级中，以拥挤度做进一步比较，取较优个体，形成种群P1(t)；

步骤5个体中的某一天的交路进行交叉操作，缩减乘务班组数目，并使用禁忌思想对某天内交路值乘安排进行变异操作，得到种群Q；

步骤7选择前N个个体产生新一代种群NPt；

步骤8判断产生更小乘务班组数目则转到步骤2.当算法进入停滞状态，乘务班组数目不再变动时，算法终止.

3 实例验证及分析

采用北京南站至天津站间的列车运营数据对本文设计的模型算法进行验算，利用经典的NSGA-II算法和改进的NSGA-II算法分别对该问题进行计算.并规定早于Ts=8:00发车的乘务交路为早发交路，晚于Te=20:30到达的乘务交路为晚至交路.列车乘务交路数据如表2所列.

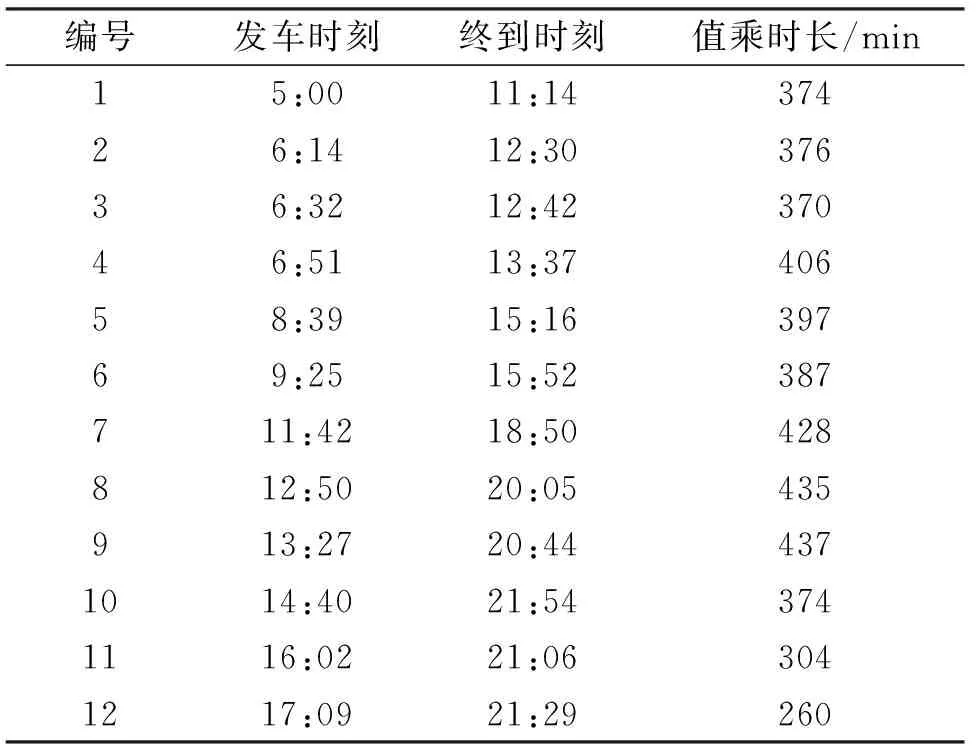
表2 列车乘务交路数据Tab.2 Crew scheduling data

对NSGA-II算法参数进行设置：T=10 080 min；Maxgen=500次；Popsize=130个；自适应概率及变异概率为PC1=0.9；PC2=0.6；PM1=0.1；PM2=0.001.

将经典NSGA-II算法和改进后的NSGA-II算法求解速度和求解结果进行比较，来验证算法及算法改进的有效性.

算法改进前后的收敛速度如图2所示.

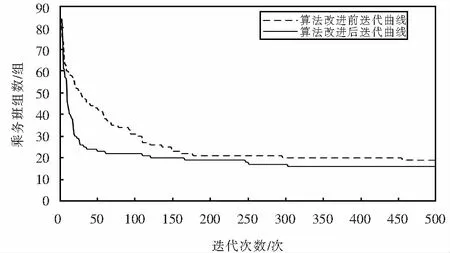
图2 算法改进前后收敛曲线对比图Fig.2 Convergence curve comparison chart before and after the algorithm improvement

通过对比算法改进前后的收敛曲线可得，经典的NSGA-II算法在迭代次数450代附近逐渐呈现出较好的收敛趋势，而改进后的NSGA-II算法在300代附近收敛稳定；改进后的NSGA-II算法收敛效率高、速度快，表现出更好的收敛性能，且求得的目标函数值更优.因此针对该问题的算法改进是有效的.

对改进前后所得最后一代Pareto解集的平均值进行对比，并将算法执行时间进行对比可知，算法改进后收敛速度提升14%，所得Pareto解集各目标函数的平均值均优于经典NSGA-II算法.算法改进前后求得的解的平均值如表3所列.

表3 算法改进前后结果对比Tab.3 Comparison of results before and after the algorithm improvement

最终求解所得的pareto解如表4所列.

表4 乘务排班问题非支配解Tab.4 Pareto solution of crew scheduling problem

解码后得出对应乘务排班计划表，其中基地住宿班组数最多和最少所对应的乘务排班计划表如表5～6所列.

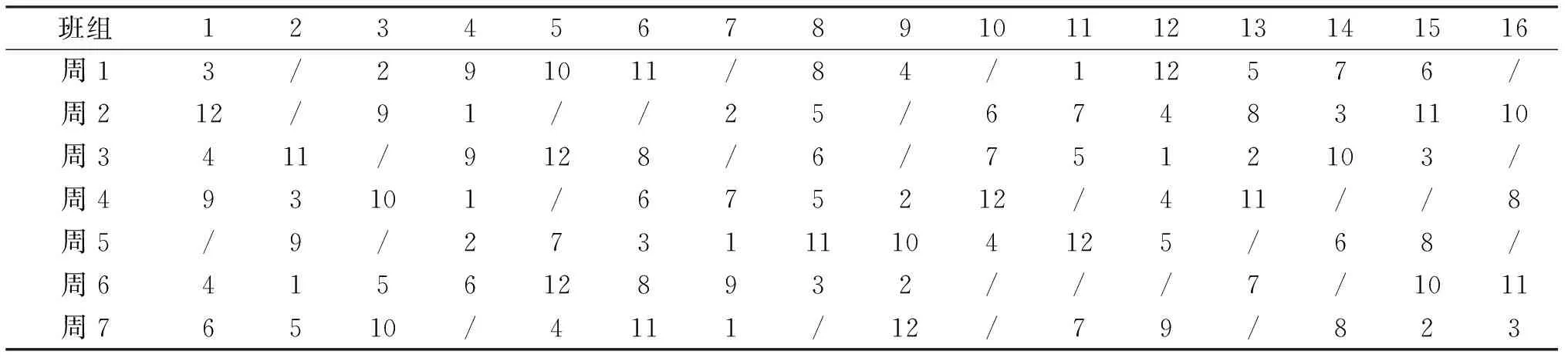
表5 当Z1=16，Z2=43 080 408，Z3=42时的乘务排班计划表Tab.5 Crew scheduling plan when Z1=16，Z2=43 080 408，Z3=42

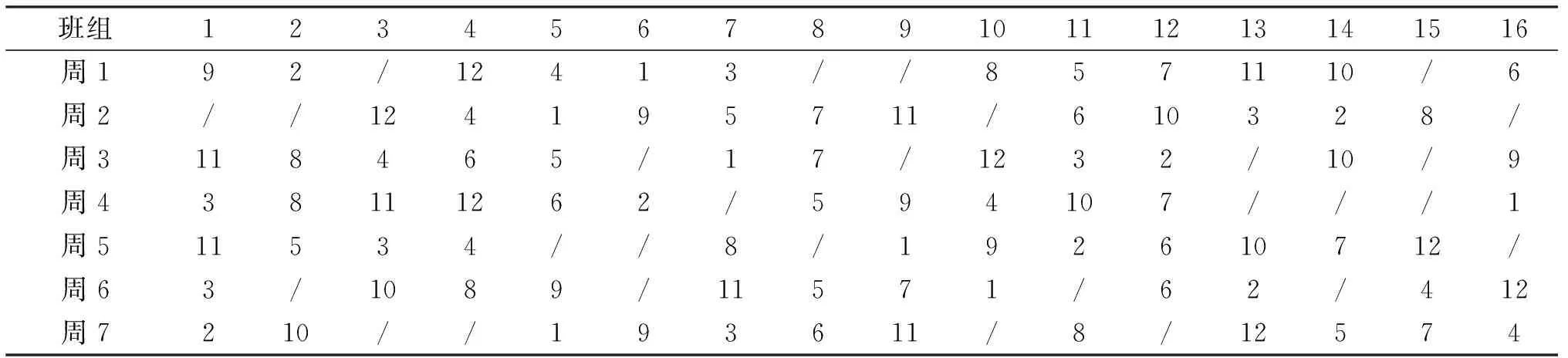
表6 当Z1=16，Z2=46 159 475，Z3=33时的乘务排班计划表Tab.6 Crew scheduling plan when Z1=16，Z2=46 159 475，Z3=33

4 结论

考虑到乘务工作中因交路出发时刻、到达时刻不同而产生的基地住宿实际，讨论因该问题产生的乘务基地住宿班组数量的优化问题，并基于指派模型，建立解决该问题的多目标优化模型.针对该模型，设计NSGA-II算法进行求解，并对算法进行了改进.最后以北京南站至天津站间的列车运行基础数据为算例，对设计的模型、算法进行验证，通过求解结果和算法改进前后计算结果的对比可得，算法改进后目标函数的求解结果及收敛速度均有了提高，从而证明了模型的正确性及算法的有效性.

乘务班组住宿优化问题，在客运段车队(间)实际工作中，有较强现实应用意义.本文未考虑在给定乘务基地住宿能力情况下列车乘务排班计划的编制，对这一问题的研究将是以后研究的重点.