欧拉不等式的一个新加强
2021-07-15 09:46:16曹嘉兴
数学通报 2021年5期
曹嘉兴
(浙江省开化县第二中学 324300)
众所周知,任意三角形的外接圆半径R不小于它的内切圆半径r的2倍,即R≥2r.这是大数学家欧拉(Euler)在1765年建立的一个不等式,由于该不等式具有简单而不平凡的特点,所以至今依然在几何不等式领域里保持着高水平的地位,关于它的各种推广和加强的研究一直是几何不等式研究的热点.贵刊就发表过多篇关于欧拉不等式的加强的文章[1-4],本文将给出欧拉不等式的一个新的加强,供大家参考与欣赏.
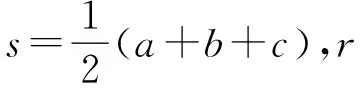
等号当且仅当△ABC为正三角形时成立.
证明在△ABC中,记BC=a边上的高为ha,∠BAC的平分线为ta,面积为Δ.



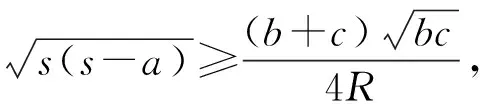

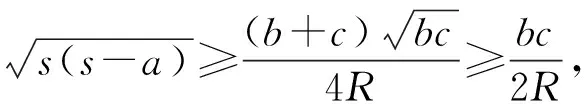
(1)
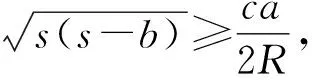
(2)

(3)
(1)+(2)+(3)得


再利用熟知的Tsintsifas不等式[5]:
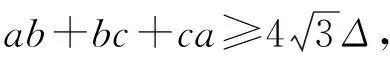

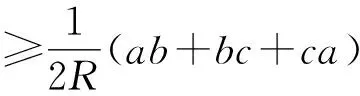
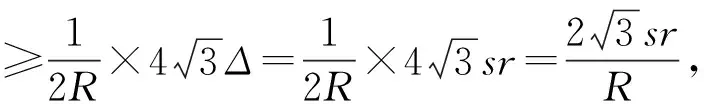


由上述证明过程不难看出等号当且仅当△ABC为正三角形时成立.
注记由柯西(Cauchy)不等式得

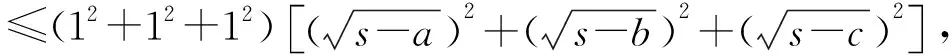

≤3(3s-a-b-c)=3s,


(4)
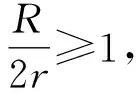
猜你喜欢
作文新天地(2022年17期)2022-11-20 01:55:07
小猕猴智力画刊(2021年8期)2021-08-27 09:15:59
中等数学(2021年2期)2021-07-22 06:21:52
数学小灵通·3-4年级(2021年4期)2021-06-09 06:28:00
中等数学(2020年9期)2020-11-26 08:07:28
中等数学(2018年7期)2018-11-10 03:29:04
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
浙江林业(2017年8期)2017-11-13 03:31:47
——浙江省衢州市开化县华埠镇中心小学
作文新天地(2017年12期)2017-06-21 15:12:54
数学学习与研究(2016年24期)2016-06-01 11:29:54

