数学归纳推理能力再探：内涵与表现①

吴惠玲 郭玉峰

(1.北京师范大学数学科学学院 100875；2.深圳外国语学校 518110)

1 问题提出

数学归纳推理能力对学生学习、数学学科发展、数学问题解决等有重要作用[1-4]，数学归纳推理与数学演绎推理一起，影响和推动数学的进展[5].《普通高中数学课程标准(2017年版)》(以下简称为“2017数学课标”)明确指出，逻辑推理素养是六大数学核心素养之一，并给出主要表现与相应的水平划分.而归纳推理作为逻辑推理的一个重要组成部分，无论教材编写还是教学实践，研究清楚数学归纳推理的内涵与学生具体表现等无疑有重要意义.

归纳推理在逻辑学、心理学和数学领域都有研究且各自关注点不尽相同.如，关注归纳推理形成过程所体现的形式共性[6]、信息加工过程[7]、任务表现[1]、归纳推理的逻辑性[8]等.归纳推理是一类重要的推理形式，与演绎推理不同.演绎推理可以得到必然的结论[9]，而归纳推理的本质是前提与结论的或然性联系，那么类比推理也属于归纳推理[8].从已有研究可见，结论的或然性和推理过程的逻辑性是归纳推理的特点.如何将二者的叙述相整合，刻画学生的数学归纳推理能力，是本研究亟待解决的问题之一.

数学归纳推理能力内涵包含的主成分是什么？它体现在数学归纳推理活动中.一些研究从推理的环节[10, 11]或数学内容特点[12]划分数学归纳推理过程，宏观认识趋于一致，即包括从特殊到一般的猜想过程以及猜想的检验过程.也有研究认为，数学归纳推理的认知过程常出现类的形成、类比、类的扩展等行为.[13]伍春兰等分析学生猜想线面垂直判定定理的过程，学生能够进行联想、自我检验.[14]对知识间关联的认识和想象与联想类比密切相关.[15]较为全面的是，Jeannotte 和 Kieran[16]从认知沟通的理论角度，给出9个数学推理词汇，描述发现相似性或差异性过程及检验猜想的过程.史亮[17]则统计《普通高中数学课程标准(实验版)》中关于归纳推理的词汇.“2017数学课标”涉及的数学归纳推理，其主要表现以及水平二和三仍较为模糊.除了理论视角，如何用实证研究分析能力结构要素？以上研究较为全面地展示了数学归纳推理能力的成分，但未明确数学归纳推理能力的主成分.在教学实践中，教师抓住主成分，更能有针对性培养学生的数学归纳推理能力.因此，明确数学归纳推理能力的主成分，借此分析数学归纳推理能力的现状，是本研究拟解决的另一方面.

总之，本文希望在数学归纳推理能力内涵基础上，结合数学归纳推理过程、相关操作词汇以及数学家的数学猜想实例，给出数学归纳推理能力的可能成分.进一步借助测试题，通过探索性因素分析法更深入揭示数学归纳推理能力的主成分，借助两次聚类分析分别得到主成分下的学生表现层次以及不同主成分的关系，从而构建数学归纳推理的框架结构，为课程建设和教学实践提供一定的参考和借鉴.

2 研究设计

小学阶段主要进行枚举归纳推理，小学高年级则逐渐开始科学归纳推理，用以理解数学概念和命题.[12]本研究希望揭示高中学生数学归纳推理的特点.考虑到测试的便利性以及数据的可靠性，研究对象选取高二年级学生.测试题编制原则是：(1)题目所涉及的数学知识是高二学生已学过的，包括高一以及高一之前的知识；(2)题目可以从特例入手，借助观察、分析、比较、联想等方式，得到猜想.(3)题目类型是学生未接触过的.教材中呈现的数学归纳推理任务为本研究测试题的设计和开发提供了思路.测试卷共3大题，2道类比题，1道归纳题.测试时长40分钟.

第1题：关于正四面体性质的类比.考察目的：(1)能否认识到正三角形和正四面体的相似性；(2)能否依据正三角形的某些性质，对正四面体的性质产生实质的联想，例如平面内关于边的问题，往往对应于空间中的平面问题；(3)能否得出正四面体性质的某个普遍规律；(4)能否用语言描述猜想.

第2题：关于空间四面体勾股定理的类比.考察目的：(1)能否认识到直角三角形和3个面两两垂直的四面体间的相似性；(2)能否根据直角三角形的勾股定理，产生空间四面体关于棱长或面积的联想，并得出普遍规律；(3)对所得的猜想，是否会检验.例如演绎证明、用具体例子增强说服力、举反例推翻等.(4)能否用语言描述猜想.

第3题：探究一元n次实系数方程的根与系数关系.考察目的：(1)能否分析特殊例子的根与系数关系，并写出特例的结论；(2)能否发现特例之间的共性和差异性；(3)如果猜出n为具体值时的根与系数关系，能否进一步得到一元n次实系数方程的普遍规律.

本研究给出数学归纳推理的8个成分假设(具体见第3.2节)，三道测试题与这些成分假设的对应关系以及具体分值(通过层次分析法得到)如表1，满分为100.

表1 研究假设维度与对应题目与分值

根据预测结果分别调整题目的提问方式、增设题目梯度、调整题量，以及调整区分度不大的题目等，形成最终测试问卷.考虑学生的数学层次分布与问卷发放的便利性，最终测试对象是山西一所重点中学(编码SX)、广东一所省级中学(编码G)、广西一所重点中学(编码GX)的高二学生，其中发放问卷425份，回收问卷395，回收率93%.回收问卷中的作废问卷是：存在一道空白的完整大题，或多于3个空白的小题，或两张问卷答案一样，这样有效问卷共368份.

表2 问卷数量情况统计

测试题的信效度来源于正式测试的数据，基于368个数据样本，本次问卷调查的信度(Cronbach α)是0.772，问卷各题项间的一致性较为合适.各维度与总分之间在显著水平为0.01(双侧)下，相关性是显著的(0.429～0.808之间).可见总分与各维度之间的相关性良好，即调查问卷具有较好的效度.因此，可对这批数据进行下一步分析，操作软件是IBM SPSS Statistics 20.

3 研究结果一：数学归纳推理能力的内涵

3.1 内涵界定

根据以上分析，借助“2017数学课标”关于逻辑推理素养的界定，“从一些事实和命题出发，依据规则推出其它命题的素养”，本研究界定数学归纳推理能力的内涵是，“从具有某一性质的一些特例(或一类事物)出发，猜想包含这些特例的一类事物(或具有共同属性的其他类事物)也具有一致的性质，并说明猜想合理性的能力.”包括以下要点：

第一，数学归纳推理是前提和结论之间存在或然性的推理形式，前提和结论之间的关系不是必然的；

第二，同数学演绎推理一样，数学归纳推理也是有逻辑的.界定中用文字语言的形式叙述这一逻辑性，也即性质传递性[8]：Ⅰ(归纳)：对于集合A和性质P，x→P，若x∈A，则A→P；Ⅱ(类比)：集合A和集合B都具有属性Q，对于性质P，若A→P，则B→P.

第三，对于高中学生的数学归纳推理，本研究更关注这样两个方面：(1)归纳：分析归纳多个特殊事物的属性，得出一类事物(包含这多个特殊事物)的一般属性，或找到具备此属性的、合适的数学研究对象集合.值得注意的是，特殊事物不一定多个，也可以是某个极端的，或具有主导性的.(2)类比：分析比较两类事物间的相似属性，从而联想到它们在其它属性上也有相似之处.

例如，一个主导作用的归纳[18]：面α和面β的夹角是θ，面积为A的多边形在面α内，猜想其投影在面β所形成的图形的面积是多少？矩形是一种便于处理且主导的特殊情形，底边平行于面α和面β的交线l，设底边为a，高为b，则投影图形的底边为a，高为bcosθ，面积为abcosθ.这可以推广到一直角边平行于交线l的直角三角形的投影面积，再推广至任意三角形的投影面积，进而推广至多边形的投影面积为Acosθ.

3.2 内涵成分再探

表3 可能的内涵成分解释

根据以上研究结果，运用探索性因素分析法提取整合数学归纳推理能力的主成分.探索性因素分析法的八个原始变量为：分析、比较、分类、联想、概括、类比猜想、归纳猜想、验证.反映象相关矩阵(表4)良好，主对角线元素的绝对值均大于0.6，基本大于0.8，主对角线外的元素绝对值绝大部分较小；KMO=0.768以及Bartlett球体检验的p值小于0.05.以上三个考虑因素均认为该问卷的数据适合做因素分析.通过主成分方法，结合先前的文献分析和表5的累积方差贡献率，相比于2个主成分而言，抽取4个主成分更好(此时的累积方差贡献率为84.141%).

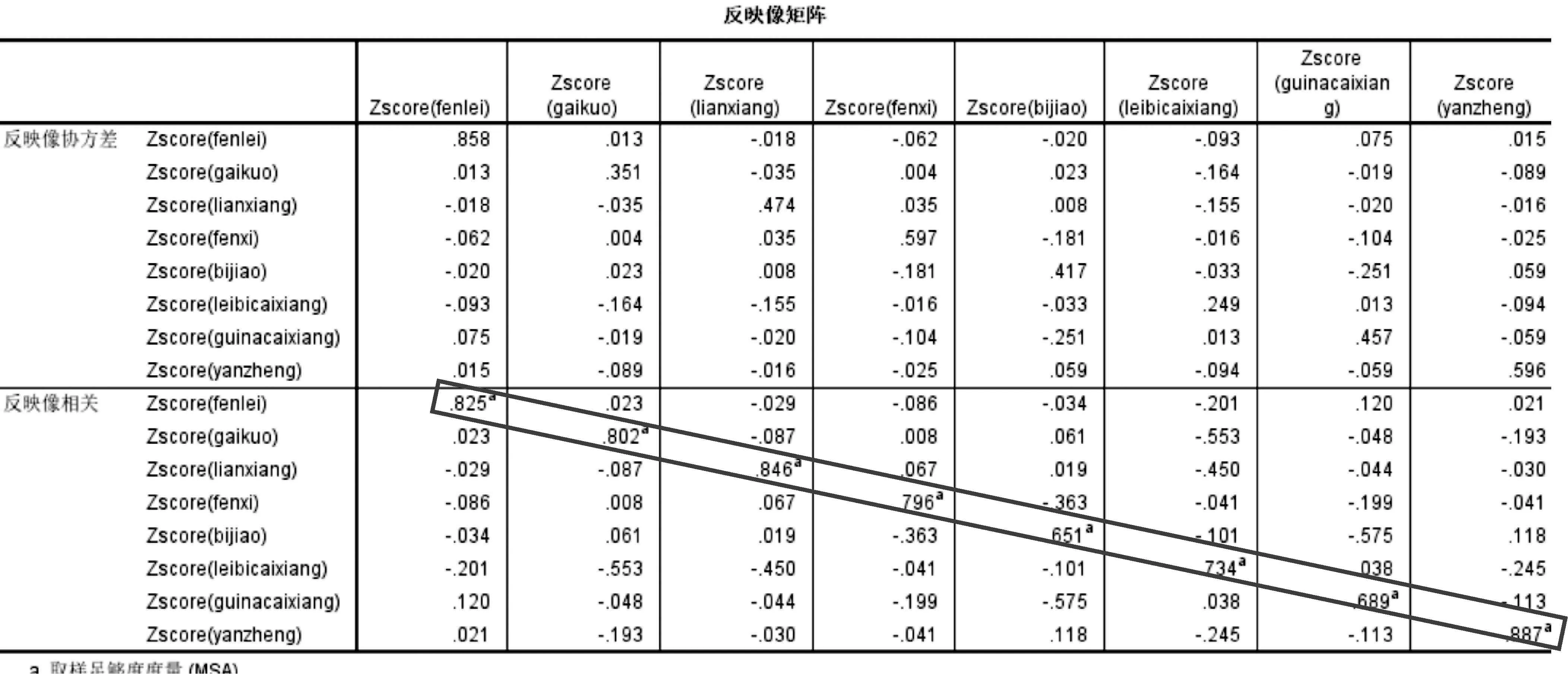
表4 反映像矩阵

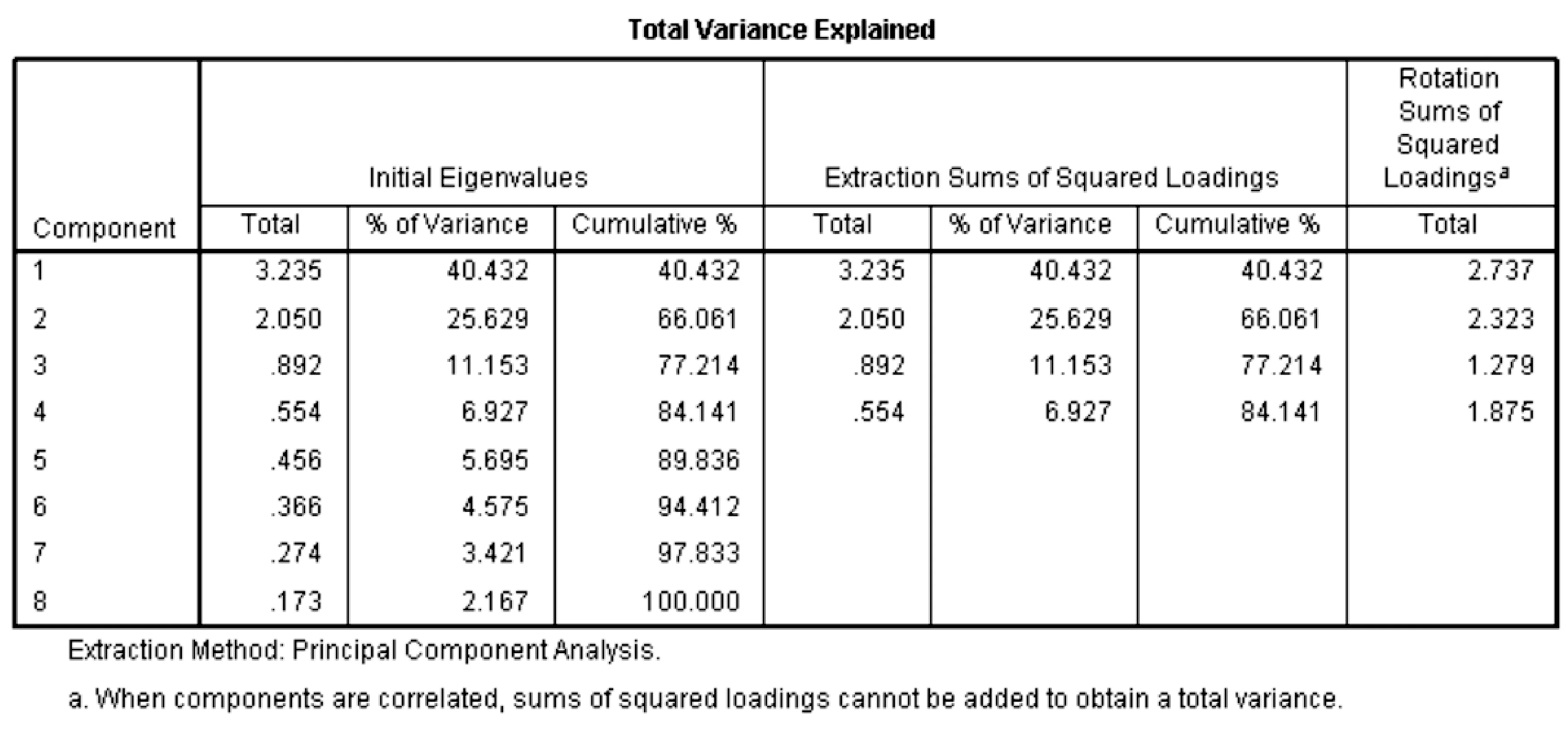
表5 解释的总方差

由于成分矩阵的维度与成分之间的关系糅合在一起，不明显，成分解释难度加大，故借助旋转变换方法得到旋转矩阵(如表6).成分1对“联想”、“概括”、“类比猜想”三个维度的载荷较大，命名成分1为联想类推；成分2对“观察分析”、“比较”、“归纳猜想”三个维度的载荷较大，命名成分2为比较递推；成分3对“分类”维度的载荷较大，命名成分3为分类；成分4对“验证”维度的载荷较大，命名成分4为验证.

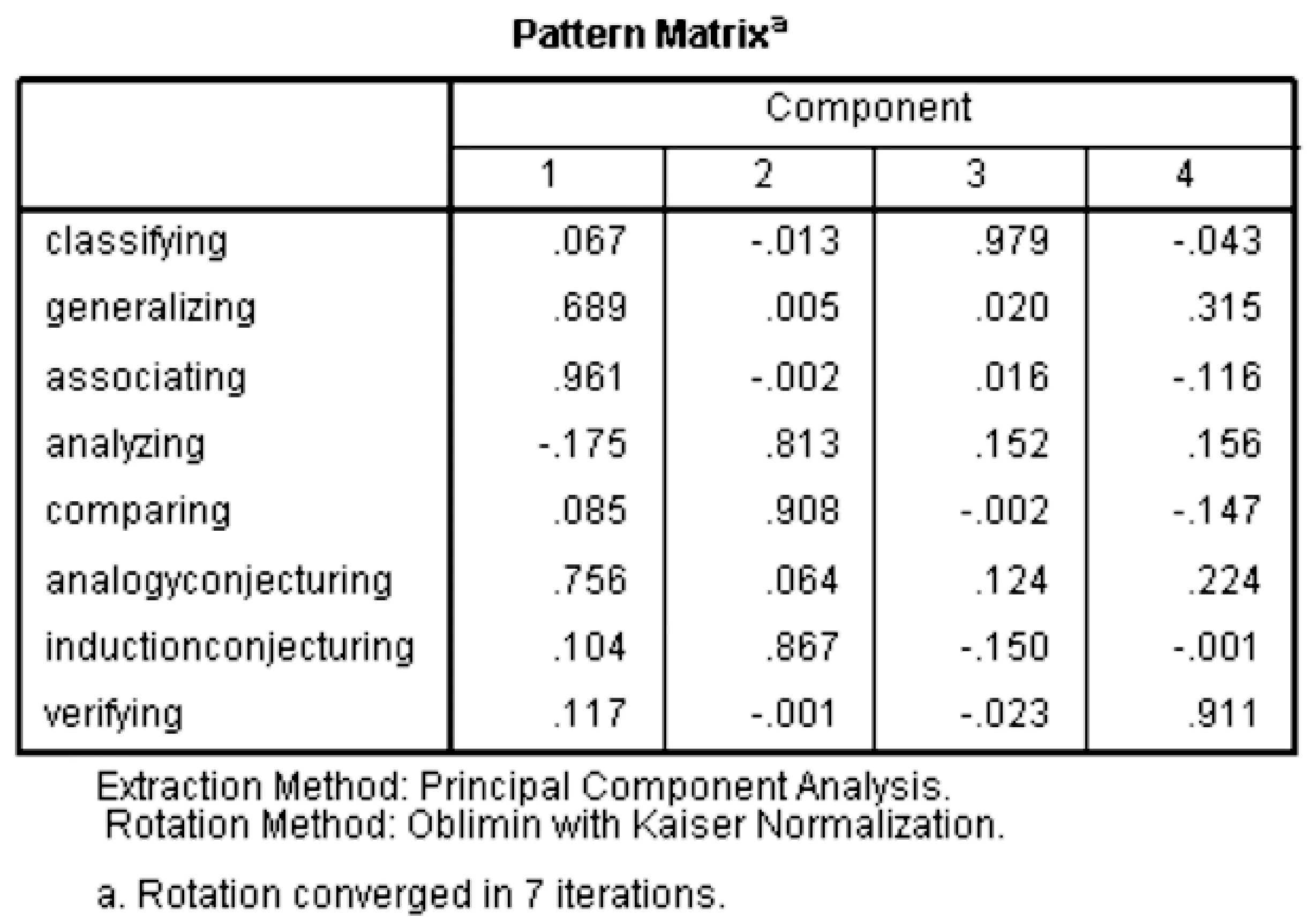
表6 抽取4个成分的旋转矩阵

4 研究结果二：高二学生数学归纳推理能力的表现

数学归纳推理能力的主成分包括分类、联想类推、比较递推、验证，学生在这四个主成分的表现如何？四个主成分间有何关系？本研究将学生测试成绩的总分、成分1得分、成分2得分、成分3得分、成分4得分作为变量，对368份测试样本进行聚类分析.借助两次聚类分析分别得到这四个主成分下的学生表现层次以及不同主成分之间的关系，得到以下数据结果.

4.1 高二学生数学归纳推理能力的表现层次

为了对学生的数学归纳推理能力按照各成分进行分层，用距离表示样本之间的关系，具体方法为：平方欧氏距离.由表7可见，第365步到第366步的聚类系数变化(7.331-5.921=1.41)与第364步到第365步的聚类系数变化(5.921-5.288=0.633)的相差较大，认为聚类为3类是合理的.再者，考虑到层次区分在实际操作的便利与明显，本研究将数学归纳推理能力的表现划分为三个层次.

表7 聚类表

根据以上分类结果，统计三个类别下学生的得分均值与得分率，如下表8：

表8 三个类别下的各变量得分均值与得分率

4.2 高二学生数学归纳推理能力的不同成分之间的关系

数学归纳推理能力的四个主成分可分别划分三个层次，反映学生可能处于的不同认知阶段，以及在这些主成分的表现有何特点.除此之外，主成分间存在怎样的关系？此时，学生的得分高低不是主要关注点，关注的是学生各个变量上分数的相似程度，也即各成分间有何关系.为此，本文选择用相似系数描述样本之间的关系，具体方法为：夹角余弦.

表9显示了层次聚类分析的聚类过程，类与类之间的距离采用一种使用较广、聚类效果较好的方法——类平均法.相邻步骤聚类系数的变化远大于前面相邻步骤聚类系数的变化，这在统计意义上认为聚类分析进行到这一步是较为合理的.[19]由表9可知，第364步到第365步的聚类系数变化(0.524-0.333=0.191)远大于第363步到第364步的聚类系数变化(0.525-0.524=0.001)，认为聚类为4类是合理的.

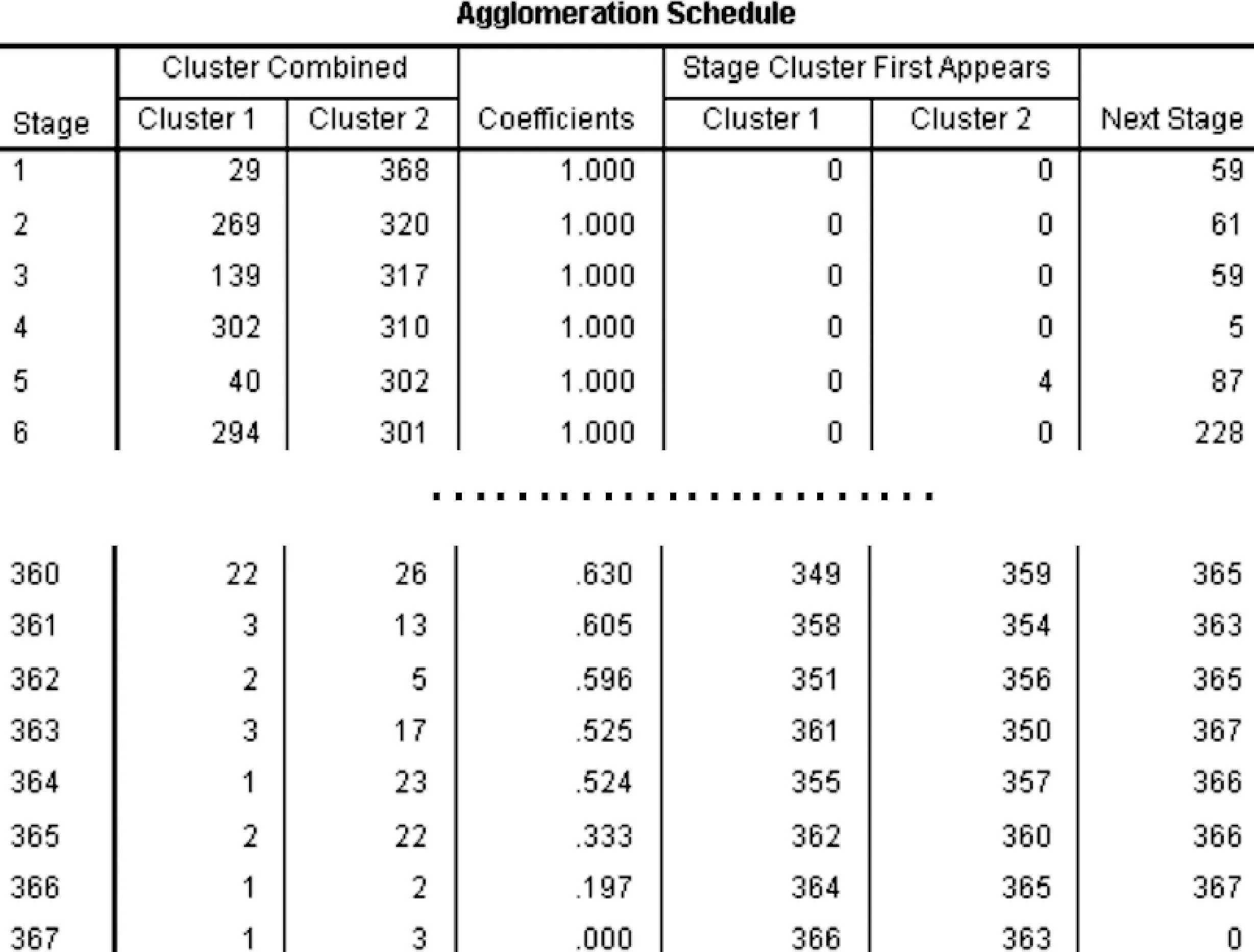
表9 聚类表

根据以上分类结果，统计四个类别学生的各成分与总成绩的得分均值和得分率，如下表10：

表10 四类情况的各变量得分均值与得分率

5 研究结论

(1)数学归纳推理能力内涵体现结论的或然性及推理的逻辑性，主成分明确推理关键环节

内涵界定中的猜想合理性要求学生意识到结论是或然成立的，从特例(或一类事物)的性质到包含这些特例的一类事物(或具有共同属性的其他类事物)的一致性质猜想，揭示了推理的逻辑性.

数学归纳推理能力的四个主成分——分类、联想类推、比较递推、验证是对假设成分的整合，突出归纳推理过程的重点与核心.前三个主成分属于从特殊到一般情形的猜想过程.分类是此过程的初始阶段，学生依据特例或某类推广，确定一类事物或其他类别，是对研究对象的分类，从而更有利于学生得到更可靠的猜想.联想类推和比较递推均是第二步，二者没有明显的递进关系.联想类推注重联想，更适合用于通常所说的类比推理；比较递推关注性质的比较，更倾向教学中所理解的狭义归纳推理.验证是猜想的检验过程，是对猜想可靠性和合理性的解释和说明，体现归纳推理结论的价值.

(2)数学归纳推理能力具有明显的三个层次

通过聚类表(表7)，将样本学生群体分成三类，分析数学归纳推理能力的各主成分表现.类别1的各项得分均值均低于类别2和3；三个类别在“分类”成分的得分均值差别较小；类别3的“验证”成分得分率远高于类别1和2的.再统计各成分下各类别学生大部分集中于哪个分数段，并分析这些学生的具体作答情况.以“分类”成分为例，思考平面中的直角三角形对应于空间中的哪种四面体时，类别1的学生较容易选择所有四面体，或有一个面是直角三角形的四面体；类别2的学生会考虑空间和平面的关系，选择有两个面互相垂直的四面体；类别3的学生会选择三个面两两垂直的四面体.以此，概括数学归纳推理能力的“分类”、“联想类推”、“比较递推”、“验证”成分的三个层次(表11)，该层次揭示了学生对事物的认识深刻程度，对简单和复杂问题的解决程度.

表11 表现层次

(3)数学归纳推理能力的“联想类推”与“比较递推”不存在明显关系，但与“分类”相关

第二次聚类分析关注数学归纳推理能力不同成分之间的关系，也即取样学生数学归纳推理能力各成分得分的波动相似程度.结合表10以及学生具体作答情况，得到以下结论：

学生在联想类推方面的表现与比较递推方面的表现不存在一致的强或弱.由表10可见：类别③的联想类推和比较递推的得分均值整体较高，超过类别②和④；但另一种情况更为明显：学生类别②的“联想类推”成分得分均值比类别④多，但“比较递推”成分得分均值比类别④少；同样，学生类别①和②之间、类别②与③之间的联想类推和比较递推的得分均值高低明显相反.进一步分析学生具体作答情况，例如，多数类别④学生能分析有n个实根的一元n次方程，猜想根与系数关系，但平面的结论类比至空间结论时，却进行无关联想；又或者，多数类别②能推广出平面到空间的较为普遍结论，但对于一元n次方程，只分析n=1，n=2的情形.本研究的归纳推理采用学界的广义观点，也即“2017数学课标”表述的“从特殊到一般的推理”，有两种推理方式：归纳和类比，此处的归纳是狭义的观点，本文的比较递推是其具体形式.数学教育把类比推理作为一类特殊的归纳推理，特别强调也就不足为奇了.对学生而言，类比推理的难度较大，往往是联想强弱的缘故.

分类对联想类推的影响存在两种情况：(Ⅰ)学生对事物的分类较弱时，其联想类推也较弱；(Ⅱ)当分类的水平较强时，对联想类推的影响不明显.表10显示，学生类别④和其他类别的“分类”成分得分均值相差较多，“联想类推”成分也如此；但类别①，②和③的“分类”和“联想类推”成分得分均值没有呈现一致的高或低.再结合学生具体作答情况，“分类”成分在6分及其以下的学生，其联想类推的得分也相对较低，例如，没有发现需要类比的性质，答非所问.“分类”得分6分以上的取样学生，其联想类推的得分波动较大.

6 讨论

随着“2017数学课标”的发布，六大数学核心素养的理论研究及其在实践中的真正贯彻落实成为关注的热点.核心素养的重要组成部分是关键能力，数学归纳推理能力作为逻辑推理素养的一部分，研究清楚数学归纳推理能力的内涵和学生表现无疑对课程实施以及教学实践有重要意义.与已有研究相比，本研究的贡献主要有以下方面：

(1)从理论上析出了数学归纳推理能力的主成分，为实践中有目的地指导学生提供了方向

数学归纳推理能力的主成分包括分类、联想类推、比较递推和验证，细化了“2017数学课标”的逻辑推理素养主要表现关于归纳推理的部分.这并不代表全面的数学归纳推理能力，而是强调在高中数学教育阶段，对学生数学归纳推理能力的发展起关键作用的不可或缺成分.主成分有利于教师在有限的时间内对学生的数学归纳推理行为做出快而准的观察与分析，发现学生的薄弱之处，从而有针对性地引导学生排除障碍；另一方面，面面俱到地评价学生的数学归纳推理能力，是困难的、不切实际的，而数学归纳推理能力的主成分可以为教师提供几个重要方面，着手评价.

(2)聚类得到数学归纳推理能力的表现层次，体现学生认知的规律性

数学归纳推理能力的三个层次是针对四个主成分进行展开的，体现了学生不同归纳推理认知阶段的特点，同时也显示了学生的发展规律，由表象到本质，由简单到复杂.例如，“分类”的层次揭示对事物认识的深刻程度，依次为：不能发现两类研究对象的关系、发现两类研究对象的非本质相似之处、发现其本质相似处或一致性.“比较递推”的层次体现学生对简单和复杂事物的解决顺序，依次为：可分析简单熟悉的特例、将简单特例的情形迁移至其他特例、将特例推广至一般情形.细化和补充“2017数学课标”关于逻辑推理素养的水平划分；有利于教师分层教学，从而有效提高学生的数学归纳推理能力.

(3)分类是数学归纳推理能力基础且重要的部分

发展学生的数学归纳推理能力时，注重“分类”成分的基础性是必要的.联想类推的提升需要较强的分类.分类是在认识事物的相似和差异的基础上，对事物进行归类；联想是通过熟悉的类别来思考一个新的类别，主要联系这两个类别的相似性.本研究结论发现，学生对事物的分类较弱时，其联想类推也较弱；当分类的水平较强时，对联想类推的影响不明显.这现象反映，在进行类比推理初期，学生更需要学会如何分类；分类到达较好的水平时，学生学习如何联想更有利于提高类比的能力，例如主动联想、相似联想和大跨度联想.也即，培养学生的数学归纳推理能力并不是一蹴而就的，需讲究策略.

总之，数学归纳推理能力研究可进一步推动数学核心素养的进展，但仍需从理论和实践两方面相互推进.本文的四个主成分呈现了学生数学学习的重要思维方式，例如，抓住问题的本质、建立待解决问题与熟悉问题的联系、用质疑的眼光看待问题等，与数学“三会”相一致，是数学核心素养的具体体现.主成分下的三个层次水平不局限于数学知识考核，转而关注学生的数学学习与思维过程，朝着数学核心素养测评的方向前进.朱立明[20]提到，深入数学核心素养的结构关系是其研究趋势之一，目前关于内涵、要素、测评等研究方面仍处于浅层阶段，需要不断挖掘与验证.因此，本文不仅补充和丰富逻辑推理素养的研究，也进一步推动数学核心素养的进展.未来，这四个主成分的创新方面也是今后进一步的研究方向.创造性的概括、类比和模式对创新的归纳推理至关重要[21].什么是创造性的分类、联想类推、比较递推和新颖的检验猜想思路，仍值得研究，这对于发展学生的创造能力具有重要作用.又如，分析学生在各种归纳推理任务情境下的表现，可以更好地补充和完善数学归纳推理能力的主成分.