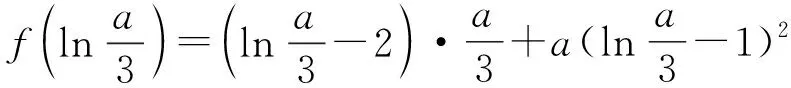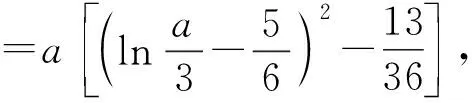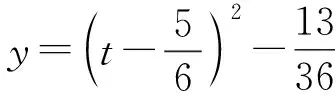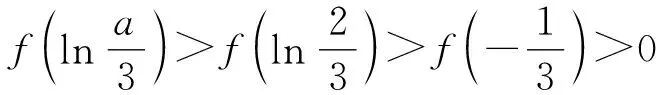何以感受数学的温度——一类“化无形为可见”问题引发的思考

刘师妤

(1.华中师范大学教育学院 430079；2.湖北省武汉市英格中学 430079)

传统逻辑基础规律之一就是排中律，通常被表述为A是B或者不是B.集合中元素与集合的关系也是如此，更确切地说，数学对象间关系往往都是如此确定.正如普通高中数学课程标准实验教科书(人教A版)主编寄语中的论述：“数学是清楚的.清楚的前提，清楚的推理，得出清楚的结论，数学中的命题，对就是对，错就是错，不存在丝毫的含糊.”数学因为有了确定性，能看得见、摸得着，才具备了“好玩”的潜质，数学才有了可抚触的温度.数学之美，美在数学语言能化无形为可见.俨然是开启自然之门的钥匙，转动它就能看到曲线的优美轨迹，握住它就能感受光辉的温度，举起它就能看到真理的距离.笔者以教学实践中的一类“化无形为可见”的问题为例，即如何运用导数工具研究含参函数的性质，一齐感受一下数学的炽热温度.

零点存在性定理，大家都不陌生，在此不再赘述.许多一线教师都站位于逻辑关系上剖析该定理，认定学习该定理的难点在于辨析这是一个判断零点存在性的定理，而非是判断零点个数的依据.实际上，从笔者及同事多年的教学实际来看，不得不说我们在“初级阶段”即判定区间两端点处函数值的正负关系，甚至在找零点大致所在区间都存在很大的困难，存在太多的“一笔带过”，如题：

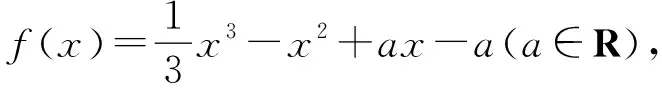
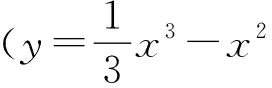
从极限的视角看问题并不是不可以，只是它的正确性要建立在对函数的性态的准确把握上，数学的奠基作用、数学的原汁原味就荡然无存了，至少在这里.

全国高考内容改革正在迈出新的步伐，数学的基础性、科学性及数学的内在理性正日渐突显出来，我们要辩证的看待数学的理性与灵活性、直觉感与严谨性.

如2015年全国高考课标(I)文科数学第21题：设函数f(x)=e2x-alnx.

(Ⅰ)讨论f(x)的导函数f′(x)零点的个数；

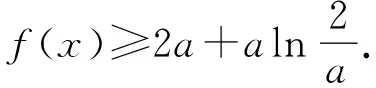
对于第(Ⅰ)问，参考答案是：

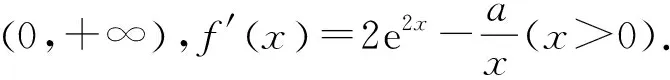
当a≤0时，f′(x)>0，故f′(x)没有零点；

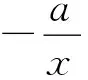
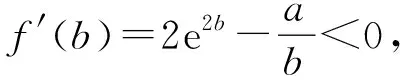
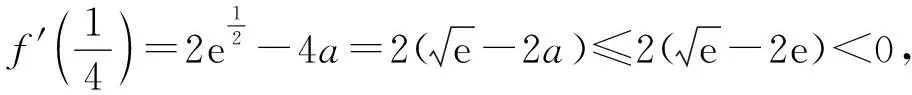
无独有偶，这一命题思路在2016和2017年的全国Ⅰ卷中竟是惊人的相似.

如(2017全国卷Ⅰ)：已知函数f(x)=ae2x+(a-2)ex-x.

(1)讨论f(x)的单调性；

(2)若f(x)有两个零点，求a的取值范围.

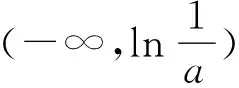
又如(2016全国卷Ⅰ)：已知函数f(x)=(x-2)ex+a(x-1)2.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若f(x)有两个零点，求a的取值范围.

分析：(Ⅱ)(i)设a>0，则由(Ⅰ)知，f(x)在(-∞,1)上单调递减，在(1,+∞)上单调递增.

又f(1)=-e,f(2)=a，

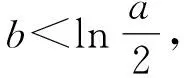
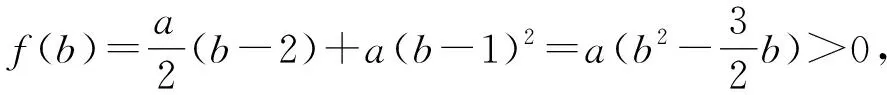
如法炮制，仍然对参数a进行讨论，

当a≥2时，f(0)=-2+a≥0，

所以f(x)在[0,1)内有且只有一个零点；

当0

综上，当a>0时，函数f(x)在(-∞,1)内有且只有一个零点.

为节约篇幅，当a=0及a<0的情形略去.

再如，题2：已知函数f(x)=xsinx，判断命题：∀M>0，至少存在一个实数x0，使得f(x0)>M是否正确.

还有一次，笔者给高三学生上“画函数图象的大致图象”的选修课时，谈到y=3x与y=2x的图象差异时，在y轴的左边并不是随着x的增大，两函数图象就越接近.学生们都感觉不可思议，莫非一直我们画的图象都太不准确？为了验证这个结论，笔者用几何画板演示了两者的图象，通过放缩图象发现：在y轴左边,y=3x与y=2x的图象均以x轴负半轴为渐近线, 当x=0时, 两图象交于点(0,1).这说明在y轴的左边y=3x与y=2x的图象从左到右开始时几乎一样, 后来y=2x的图象变化加快使得y=2x与y=3x的图象逐渐远离, 而当x经过某一值x0以后y=3x的图象变化加快使得y=2x与y=3x的图象又逐渐接近, 直到x=0时两图象交于点(0,1).原本以为学生会“善罢甘休”，哪知学生还不依不饶：“老师不常说‘眼见不一定为实’嘛，那这个x0究竟为多少呢？

文[4]中谈及到“要是没有数学，你将无从理解，是什么东西让一架巨型喷气式飞机浮在空气中”“数学允许我们将另外一些不可见——亦即尚未发生之事——变为可见，如用微积分预测明天的天气”，都揭示着一个道理：合乎情理的事情背后是确定的、实在的对象或机理在发挥着作用.熟读数学分析的读者会愈加深刻感受到数学学科的温度.该门课程以严格的极限定义为基础，切切实实的分析无穷小量；它又不仅限于在一定范围内探讨极限、微分与积分的性质，它在于体现一种问题分解、问题向确定性转化(此过程常会导致新的层次的问题的产生)的策略与数学本原思想.

不妨再看几个类似的例子，以探求合理性背后的确定性.

题3(2014福建)：已知函数f(x)=ex-ax(a为常数)的图象与y轴交于点A，曲线y=f(x)在点A处的切线斜率为-1.

(Ⅰ)(Ⅱ)略；

(Ⅲ)证明：对任意给定的正数c，总存在x0，使得当x∈(x0,+∞)时，恒有x2

对于第三问，大部分学生都可以感受到一种很强的合理性，随着x的增大，指数型函数y=cex(c>0)的函数值总会超过幂函数y=x2的函数值，但难以用数学的方式予以表达.在注重前后设问联系(指数函数与一次、二次、三次函数的关系)的基础上，发现证法.

由(Ⅱ)知，当x>0时，x2

从而h′(x)<0,h(x)在(0,+∞)上单调递减，

故对任意给定的正数c，总存在x0∈(x0,+∞)时，恒有x2

题4证明：对任意正数a，存在正数x，使不等式成立.

故h(x)>h(0)=0，

原不等式即为ex-(1+a)x-1<0.

令g(x)=ex-(1+a)x-1，

则g′(x)=ex-(1+a).

由g′(x)=0得ex=1+a，解得x=ln(1+a)，

当0

当x>ln(1+a)时，g′(x)>0.

故当x=ln(1+a)时，g(x)取最小值g[ln(1+a)]=a(1+a)ln(1+a),

故s(a)

即g[ln(1+a)]=a-(1+a)ln(1+a)<0.

因此，存在正数x=ln(1+a)，使原不等式成立.

M·克莱因在他的著作《数学——确定性的丧失》中提到数学自古希腊起的两千年里，经受了灾难并最终战胜了它.从“无理数的发现”到演译推理下建立的几何公理体系，从“无穷小是零吗？”到微积分在诸多领域的成功应用，从“悖论的产生”到重新考量数学基本结构的有效性，表面上数学的确定性正一步步丧失，实质无尽的争论、质疑与释疑会把数学推到一个更辉煌的高峰.同样，我们平时的学习中碰到的看似难以“确定”的内容又何尝不是我们数学学习中思维提升的助推剂、转化剂呢.