寻问题模型之源 挖教材潜在之能①

吴莉娜

(江苏省常州高级中学 213003)

“数学教材为‘教’与‘学’活动提供学习主题、基本线索和具体内容，是实现数学课程目标、发展学生数学学科核心素养的重要教学资源.”[1]面对各种教学情境，怎样利用好教材的“源”，是每一个教师需要研究的问题.本文以2017全国新课标平面向量试题为载体,探索高中数学教学如何回归教材，挖掘教材的潜在功能，对教材典型问题进行引申、推广，在教学中有意识地引导学生寻找问题模型的源头，运用数学思想方法解决问题，提高学生的思维品质和创造性解决问题的能力，从而提升学生的数学素养.

1 问题由来

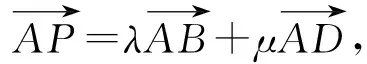
本题题面简约，背景清晰，主要考查：(1)平面向量基本定理的应用；(2)平面向量的坐标运算；(3)直线与圆的位置关系.

解析如图1以B为坐标原点，BC，BA所在直线分别为x轴，y轴建立平面直角坐标系，

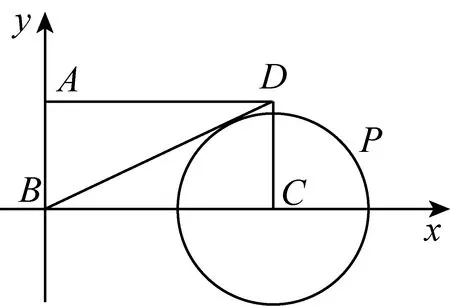
图1

则A(0,1)，B(0,0)，C(2,0)，D(2,1)，

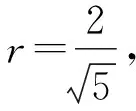
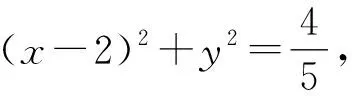
设圆C上任意一点P(x,y)，

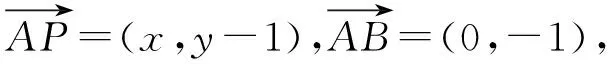
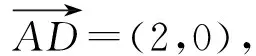
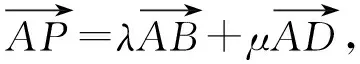
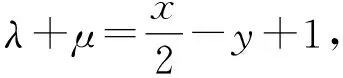
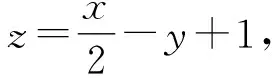
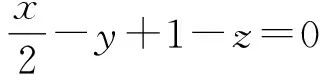
又点P(x,y)在圆C上，

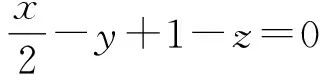
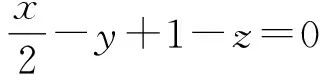
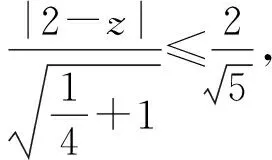
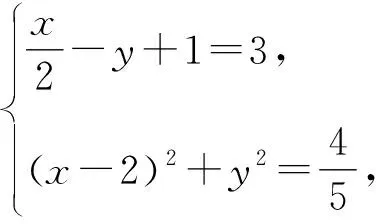
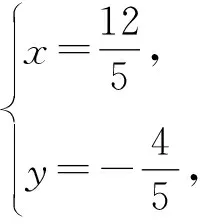
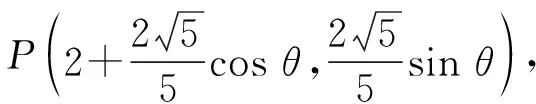
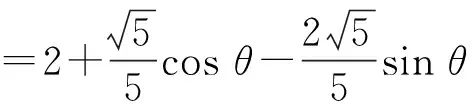
=2-sin(θ-φ)≤3，

多角度、多层次地考查学生对基础知识、基本技能以及数学思想方法的掌握情况.诸如此类的，已知图形关系求基向量系数问题或者已知系数条件求图形的有关问题，在历年的高考真题与模拟题中屡见不鲜，能有效地考查学生思维的灵活性和敏捷性.而学生在解决此类问题时，往往思路并不清晰且解题繁琐，得分率普遍不高.

2 追本溯源

针对这个问题的典型性，笔者认为有必要对其展开研究，细细品味，发挥试题教学的价值.于是研究了几套教材向量部分的编写，发现教材中都可以找到此类问题的源头所在，下面以人教版和苏教版教材来谈一谈.

人教版教材

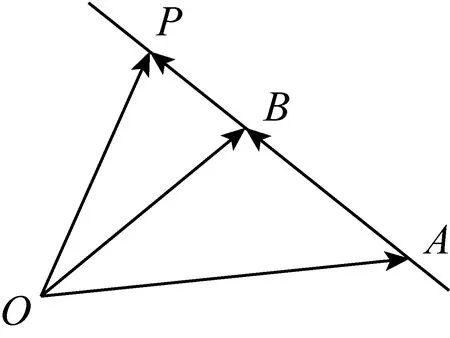
图2

苏教版教材

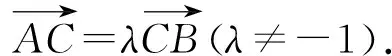
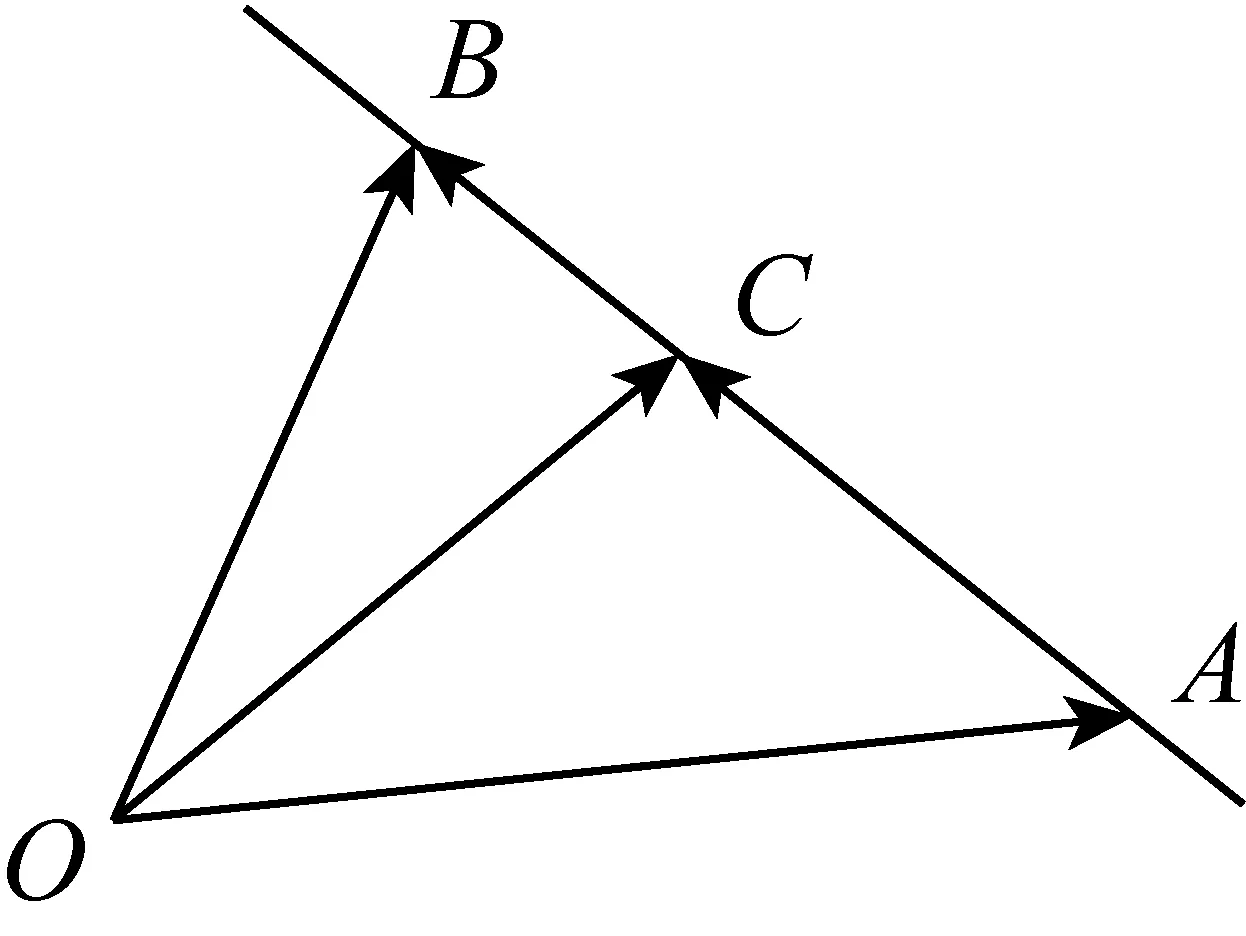
图3

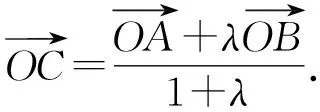
3 拨云见日

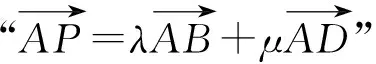
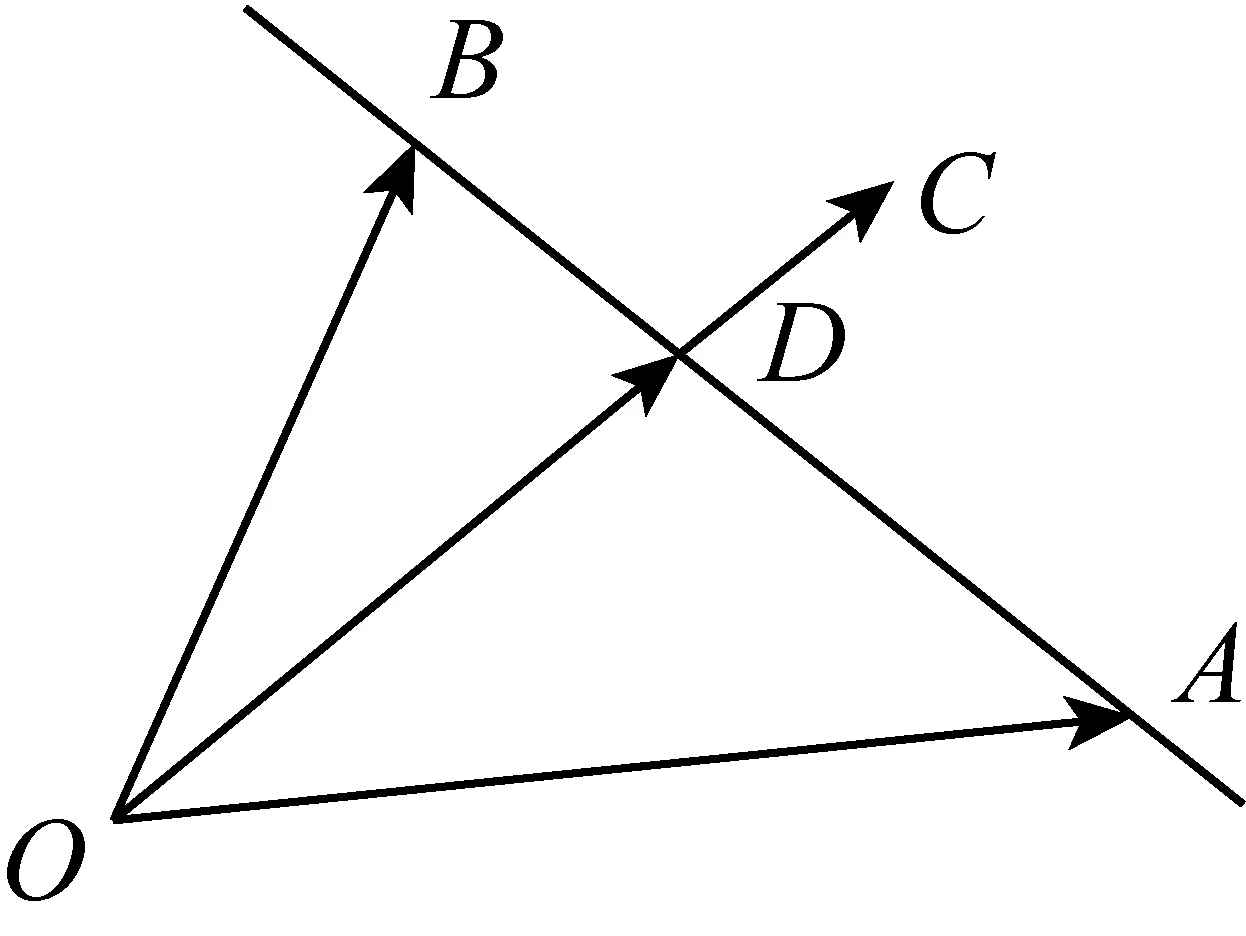
图4

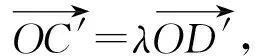
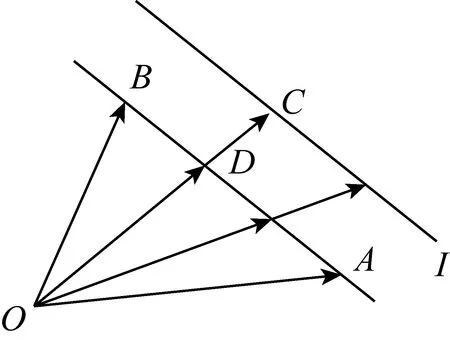
图5

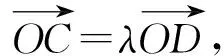
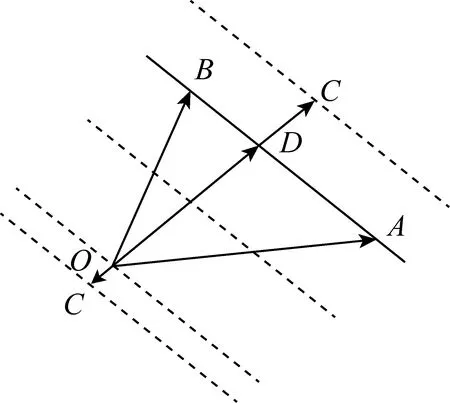
图6

因此由等和线结论2，我们可以另起炉灶来建构新的思路解决引例.

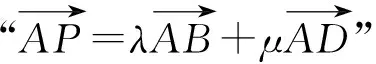
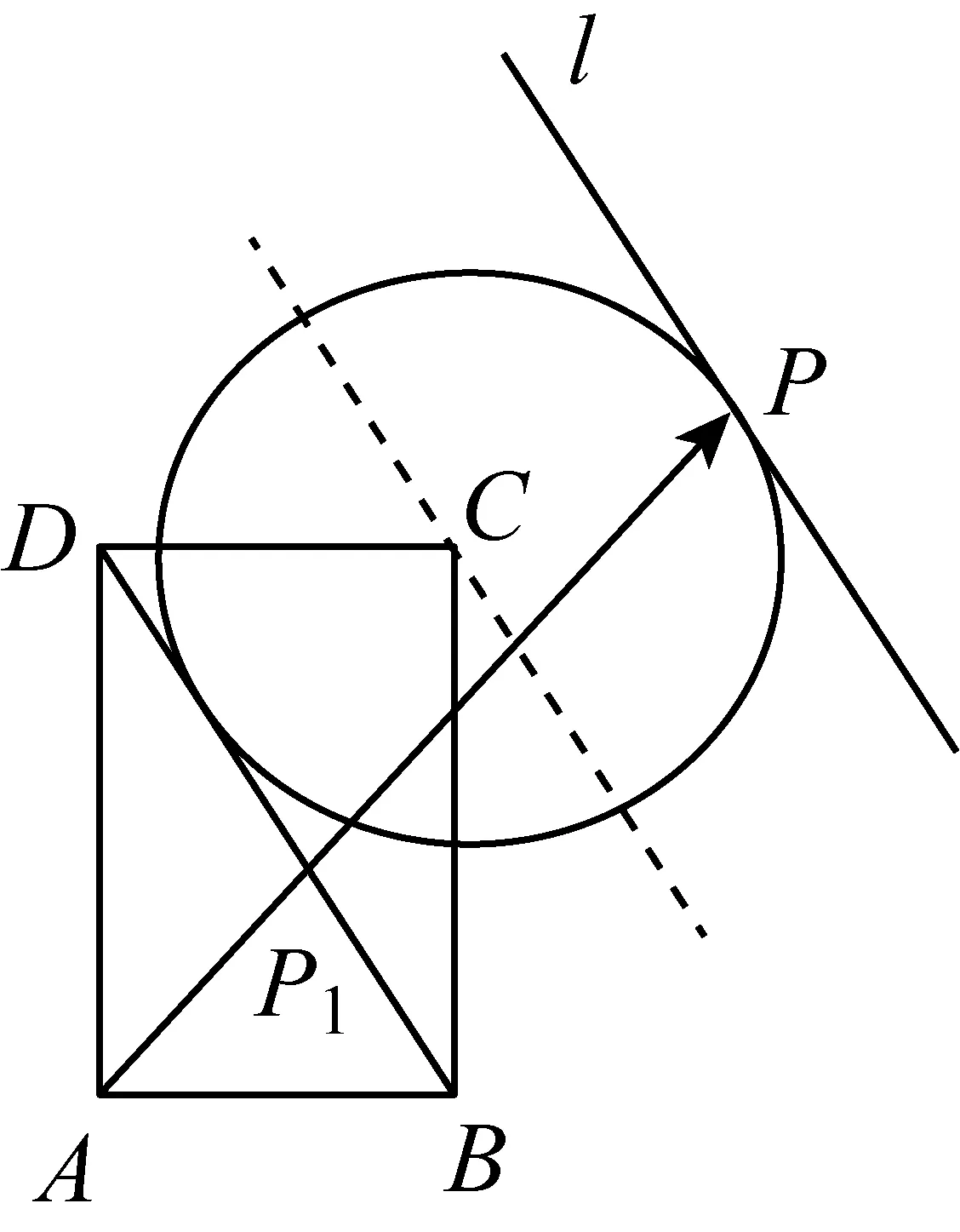
图7

4 延伸拓展

虽然引例的解题思路和方法并不唯一，但是相比较而言，利用向量等和线结论求解向量线性运算中共起点基向量的系数和问题，比建系转化为代数问题求解更显自然和流畅，能有效降低知识综合性要求与运算能力要求.不仅拓展了学生对平面向量的认知，而且对培养学生数形结合思想大有裨益.在历年的全国高考题、模考题中，以等和线为背景的平面向量问题受到了命题者的青睐.

应用1等和线结论应用于基向量系数的线性关系式aλ+bμ的最值问题.

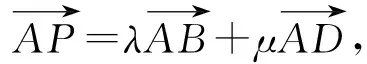
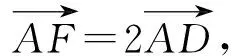
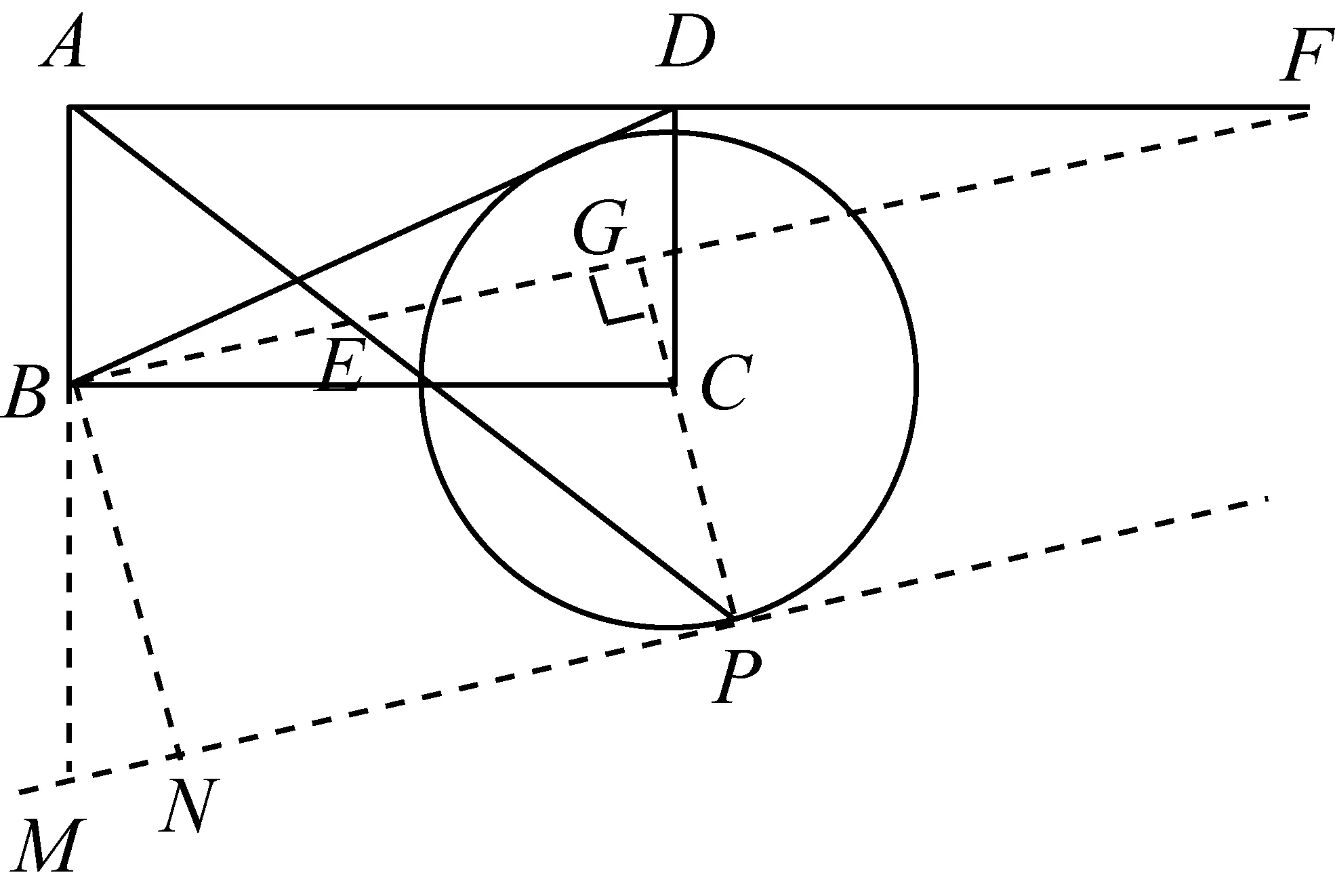
图8

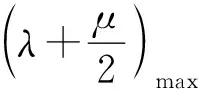
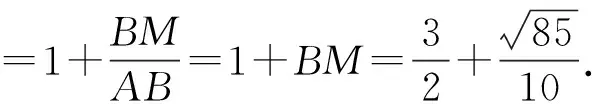
分析本题通过改编将系数和问题推广为系数的线性关系式，由于向量的数乘运算从形的角度，可以通过将原向量在共线的前提下，进行伸长、压缩等操作，那么从理论上来说，所有的系数之间的线性关系，我们都可以通过调节基底向量，使得所求系数线性关系变换为两个新基底向量的系数和问题，然后寻找到系数的线性关系式取得最值的等和线，利用等和线结论2解决问题.

应用2等和线结论应用于条件中三个向量不共起点时基向量系数和的问题.

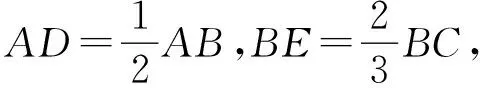
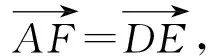
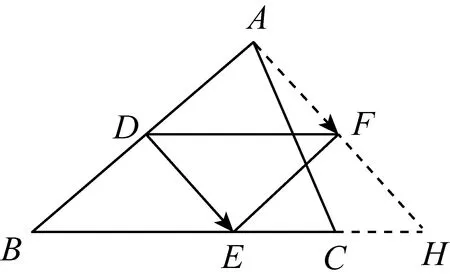
图9

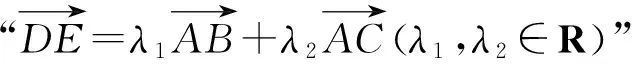
应用3等和线结论应用于基向量的终点运动变化的一类动态问题.

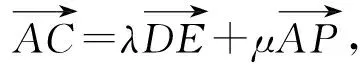
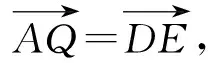
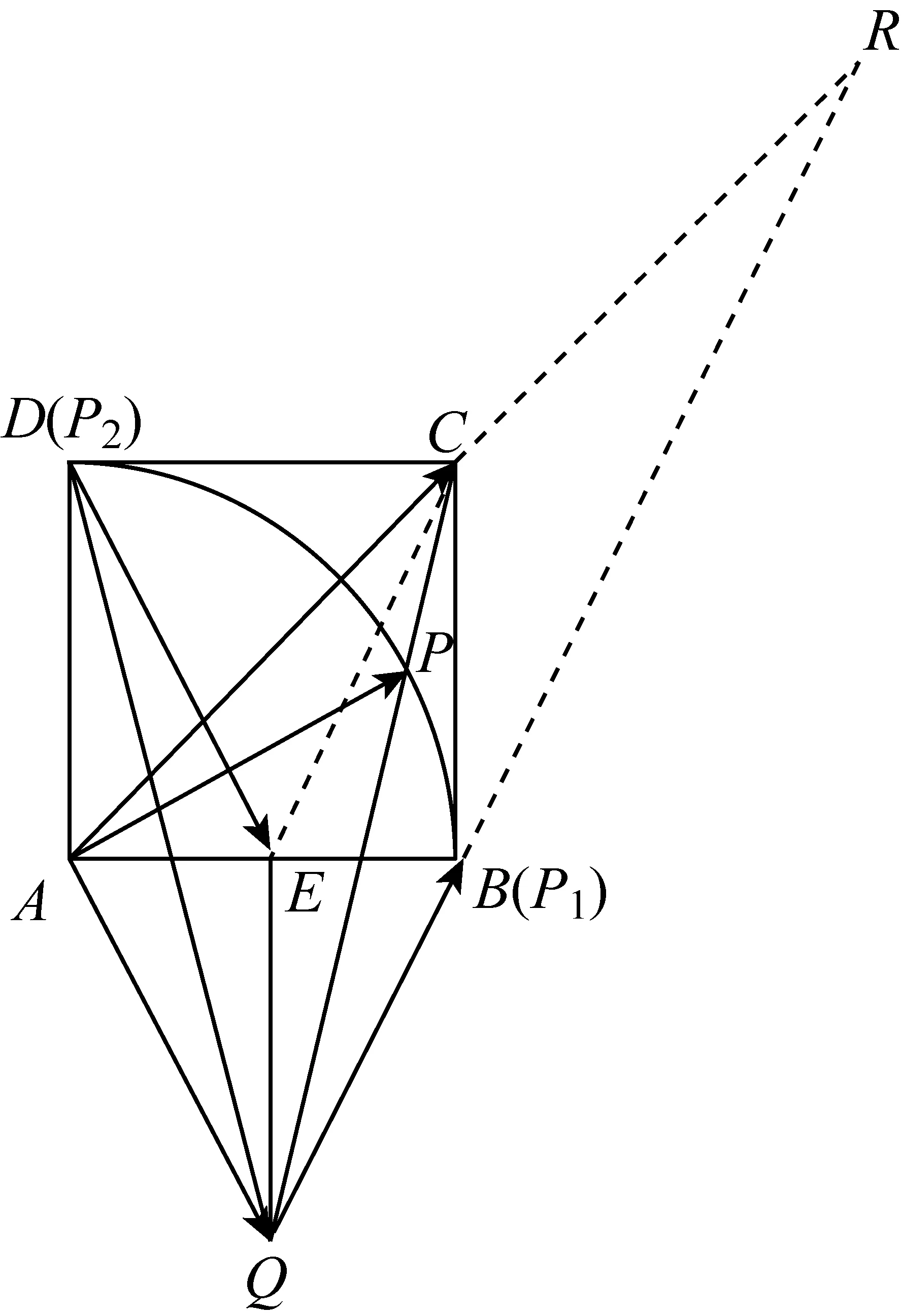
图10

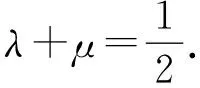
5 源清流澈

“向量理论具有深刻的数学内涵、丰富的物理背景.向量既是代数研究对象，也是几何研究对象，是沟通几何与代数的桥梁.”[1]因此，平面向量是高中数学的核心内容和重要思想方法，也是高考中经常考查的内容.怎样让学生理解向量的内涵，充分认识向量的“桥梁”作用，在教学中，我们从一个典型问题出发，通过以上变式问题的层层深入探究，让学生发现利用等和线结论解决向量线性运算的基底系数和问题，可以巧妙的将复杂的求值、最值等一系列代数问题转化为几何图形问题，将具体的代数式运算转化为距离的长度比例关系问题，用统一的数学模型沟通了相关问题，完美地呈现了数形结合思想在解题中的优势，提高了学生的思维品质和创造性解决问题的能力，从而达到提升学生数学素养的目的.

费里德曼在《怎么学会解数学题》中提出：“如果我们着手解答一道习题，那么，第一件事就想知道：这是道什么题？它是什么形式，属于哪种类型？换句话说，就是需要识别给定习题的类型.”[2]教材中的每一个例题、习题的设置都有其目的和作用，体现着本节知识所应达到的能力要求，教学不仅要紧扣教材中的基础知识，还要发现和应用教材习题中蕴含的数学思想方法，更要挖掘和利用教材习题潜在的功能.因此，指导学生回归教材，依“纲”固“本”，挖掘教材的潜在功能，对教材典型问题进行引申、推广，教材素材之“源”清楚，学生思维之“流”才能清澈，“源于教材，高于教材”，带领学生领略更靓丽的风景.