一类变系数迭代数列的收敛性

黄永忠, 雷冬霞

(华中科技大学 数学与统计学院，武汉430074)

1 引 言

(1)

定义的数列{xn},其中an>0(∀n∈*).这个数列是单增的，且有如下结论：

引理1由式(1)定义的数列{xn}收敛当且仅当正项级数∑an收敛.

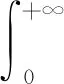
最后以引理1的证明结束本节.

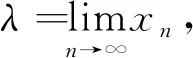
从而由比较判别法得到λ-p∑an收敛，因此∑an收敛.

另一方面，设正项级数∑an收敛. 对所有正整数n,有

由比较判别法知，级数∑(xn+1-xn)收敛，从而数列{xn}收敛.

为简便计，涉及数列等价或极限时，省略n→∞,比如an→0就是an→0(n→∞).

2 数列{xn}的收敛性

下面依次考虑正项级数∑an收敛、发散时与数列{xn}相关的等价量.

2.1 级数∑an收敛的情形

容易验证下面的简单不等式性质：

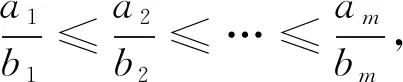
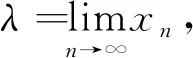
证证明思路来自文[1]例1.7.8(2)的解，但那里有两个地方不严谨(最终结论是正确的).一个是等价量加法性质需要有条件但没指明，另一个是那里的n0=n0(ε)表明n0与l无关，这正是需要论证的.对此，下面给出不同的处理.

由数列{xn}单增且收敛知λ≥xn≥x1>0,从而有

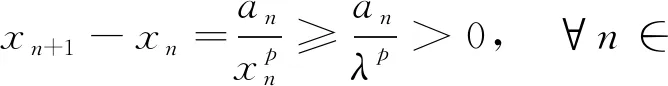
因此，∀m,n∈*有

(2)

于是由引理2得

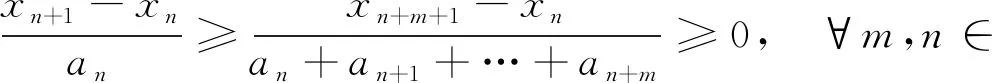
(3)

(4)

综合式(2)和式(4)，当n>n0时对任意正整数m有

令m→∞,注意到∑an收敛，得

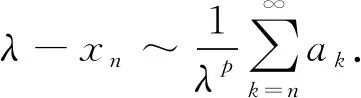
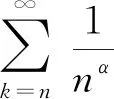
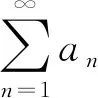
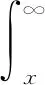
(5)

知

下面的引理3建立了一个等价结论.

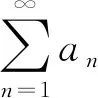
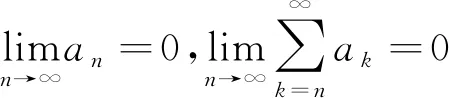
和

令m→∞得到

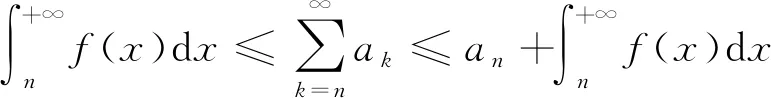
于是由两边夹定理得到

2.2 级数∑an发散的情形

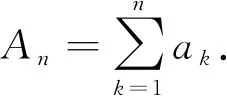
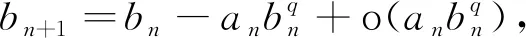
证由Stolz定理得到

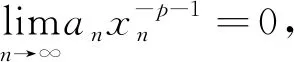
证由引理1知数列{xn}是发散到+∞. 令yn=1/xn则yn→0且由式(1)和Taylor公式有

3 应 用

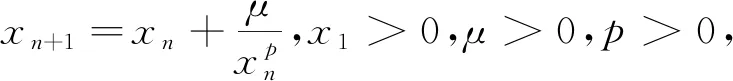
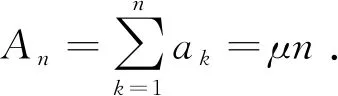
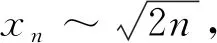
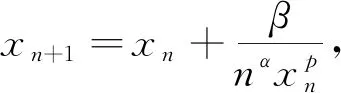
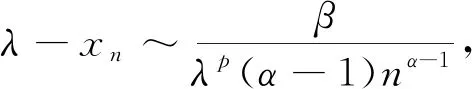
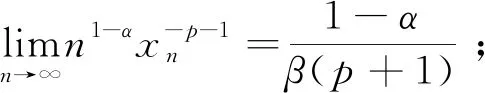
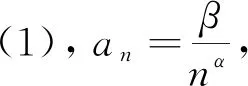
于是结论(ii)成立.

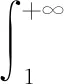
类似地，有

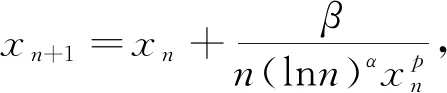
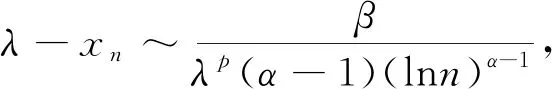
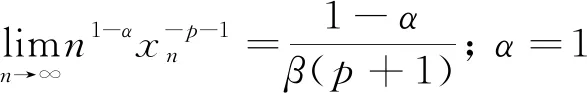
对于例3，仅给出引理3的相应验证如下：

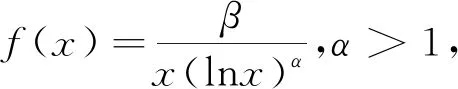
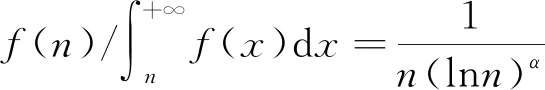
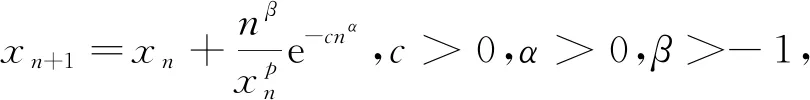
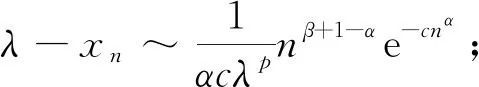
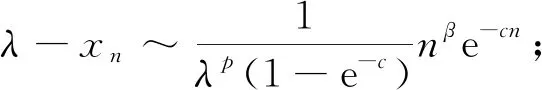
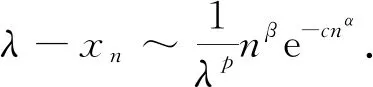
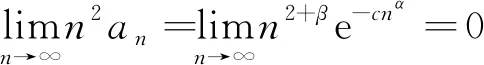
对α>1由

-c(n+1)α+cnα～-αcnα-1→ -∞,

有

因此由命题1和式(5)，对α<1有

由文[3]命题3, 记

则

最后由命题1得证(ii)、(iii).

4 结 论

本文对文[1]的一道例题进行推广，得到由变系数迭代式所定义数列的相应收敛性结果，在具体应用中涉及级数余项与其对应余积分的等价关系.应用例子本身也是一些结论的推广，展现了这种推广的有效性.

致谢作者非常感谢文献[1,3]对本文的启发以及审稿专家提出的宝贵意见.