Heusler合金Mn2V0.5Co0.5Al的晶体结构与磁性能研究

王 高，卢志红，樊帅锋，袁晓娟

(武汉科技大学省部共建耐火材料与冶金国家重点实验室，湖北 武汉，430081)

Heusler合金是一类具有丰富物理性能的磁性功能材料，具有较高的自旋极化率和居里温度点[1-3]。Heusler合金不仅能带结构特殊，即在一个自旋通道上表现出半导体性质，而在另一个自旋通道上表现出金属性质，表现为半金属特性[4]，而且在费米能级上能展现完全的自旋极化率(100%)，在提高自旋电子器件性能方面能够提供有效的自旋注入，有望成为潜在的理想自旋电子材料[5-6]。为了能满足实际应用需求，需要Heusler合金材料具有高于室温的居里温度点以及半金属稳定性。现有研究证实，低磁矩合金的自旋转移机制更具效率，其能在局部磁矩和传导自旋电子之间通过角动量传递，利用较小的自旋极化电流即可实现磁性合金的磁矩反转[7]。因此，在众多的半金属材料中，兼具高居里温度点、高自旋极化率和低磁矩特性的Heusler合金具有更广阔的应用前景[6,8]。

本研究拟在Mn2VAl合金的基础上进行掺杂，研究显示，对四元合金性能的预测应考虑与之相近的母相三元Heusler合金的性质[15-16]，如Mn2VAl和Mn2CoAl合金，均具有较高的居里温度点(760、745 K)和高自旋极化率，但其磁矩也较高(±2.0 μB/f.u.)[17-18]。本研究在三元Heusler合金Mn2VAl的基础上掺杂Co元素，基于密度泛函理论(DFT),采用第一性原理赝势方法，对其电子结构、磁性及半金属特性进行计算，以期为高性能新型自旋电子材料的研发提供参考。

1 模型建立与计算方法

本研究用模型是基于一个16原子的晶体单胞，图1(a)和图1(b)分别为两种三元Heusler合金的典型晶体结构，即有序L21结构和XA结构，图1(c)为本研究计算用理想16原子四元合金Mn2V0.5Co0.5Al的晶胞结构。对于三元Heusler合金X2YZ(X、Y通常为过渡族元素，Z指代主族元素)，50%B2无序结构模型仅改变一对YZ位置的原子占位，而100%B2无序结构则对应两对YZ位置的原子交换[12]。在具有XA结构的Mn2CoAl有序晶胞中，Mn和Co原子的占位则可以将8c位置分裂成4c(0.25，0.25，0.25)和4d(0.75，0.75，0.75)。根据经验规则，不同原子在晶胞结构中的占位顺序与各类原子的价电子数有关[18]，价电子数较多的原子倾向于优先占据8c位置。

(a) L21结构 (b) XA结构 (c) Mn2V0.5Co0.5Al晶胞结构

本研究以密度泛函(DFT)理论为基础，利用VASP软件结合第一性原理对Heusler合金的结构进行模拟计算。利用全势线性缀加平面波(FP-LAPW)方法生成的广义梯度近似(GGA)方法处理电子之间的交换关联能[21]，计算后使各离子状态均满足能量收敛标准(小于10-5eV/atom)和力收敛标准(小于0.1 eV/nm)。为提高计算精度，弛豫和静态计算均采用Monkhorst-Pack方法产生的相同的11×11×11格点精度进行布里渊区能量积分，设置高斯展宽为0.2 eV，平面波截断能为450 eV。

2 结果与讨论

利用第一性原理，计算得到常规Mn基三元Heusler合金和Mn2Co0.5V0.5Al四元合金结构有序及结构无序时的极化率和能量改变，如表1所示。表1中，a表示完全有序结构合金的优化晶格常数；P表示材料自旋极化率，P=(N↑-N↓)/(N↑+N↓)，N↑、N↓分别为费米能级处自旋向上和自旋向下的电子数；M表示合金的原胞磁矩；ΔE表示合金在B2结构无序时的能量改变量，ΔE=EB2无序-E有序，EB2无序、E有序分别对应B2无序结构与完全有序结构的形成能。计算结果显示，合金磁矩都遵循Slater-Pauling规则(Mt=Zt-24，Mt为原胞磁矩，Zt为原胞总价电子数)[22]。图2所示为Heusler合金有序结构与B2无序结构的能量差与无序程度的关系。

结合表1和图2可知，相比于MnYAl(Y=Ti、V、Cr、Fe)，Y为Co时更不易于形成B2无序结构，且在 50%B2无序时仍能保持100%的自旋极化率；由文献[17-18]可知，Mn2CoAl合金居里温度为745 K，远高于室温，略低于Mn2VAl的居里温度点760 K。由第一性原理计算得到Mn2V0.5Co0.5Al合金的50%B2、100%B2(Mn2与Al原子交换位置)无序结构与有序结构的能量差分别为0.0321、0.0465 eV/atom，其能量差均高于对应的Mn2VAl结构发生B2无序时的能量差，由此可见，Co原子掺杂在Mn2VAl中所形成的Mn2V0.5Co0.5Al合金一定程度上能够抑制B2无序

表1 Heusler合金的晶格常数、极化率及能量差计算值

图2 Heusler合金能量差随B2无序程度的变化

结构的形成。四元Mn2V0.5Co0.5Al合金的50%B2无序和100%B2无序结构的态密度(Density of state，DOS)如图3所示，其理想有序结构有着完全自旋极化率，在发生100%B2无序情况时，自旋极化率可达90.8%。

图3 不同结构Mn2V0.5Co0.5Al合金的态密度图

利用第一性原理对Mn2V0.5Co0.5Al合金的理想结构进行计算，得到基于平衡晶格常数的向上能带、向下能带及能态密度图，分别如图4和图5所示。由图4可以看出，合金自旋向上方向上存在明显的直接带隙(带隙宽度约为0.167 eV)，表现出半导体性质；费米面落在带隙中部位置，自旋极化率为100%；合金向下的自旋通道中，价带穿过费米能级，使得电子能轻易进入导带，表现为金属性；由此可见，四元Heusler合金Mn2V0.5Co0.5Al具有半金属性。由图5可见，合金的总态密度图(Total density of state，TDOS)表现出能态劈裂，即自旋向上和自旋向下通道呈现不对称性，证实该合金具有磁性性质；另外，Mn1-3d、Mn2-3d、Co、V的原子分态密度(Partial density of state，PDOS)具有不对称性，Mn1-3d与Co原子的分态密度图显示，其在相同能量区间(-2.15～-0.87 eV)的杂化轨道有一定程度的重叠，而Mn2-3d与V原子在3d轨道上，同样具有电子能级轨道之间的相互杂化作用。对比发现，Mn2V0.5Co0.5Al合金总态密度主要来自于Mn1-3d态密度的贡献，很大程度上是因为在具有16原子的理想晶胞中，Mn1的原子数较多且原子之间受轨道杂化作用的影响。与此对应，计算得到Mn2V0.5Co0.5Al合金的Mn1、Mn2、Co、V、Al原子磁矩分别为1.415、-2.801、-0.650、-0.763、-0.006 μB，原胞磁矩为0 μB/f.u.，与相应的理论磁矩一致，这是因为理想晶胞结构中原子之间的磁矩有正负值，这使得四元Heusler合金Mn2V0.5Co0.5Al的晶胞磁矩得到完全补偿。

图4 Mn2V0.5Co0.5Al合金的能带

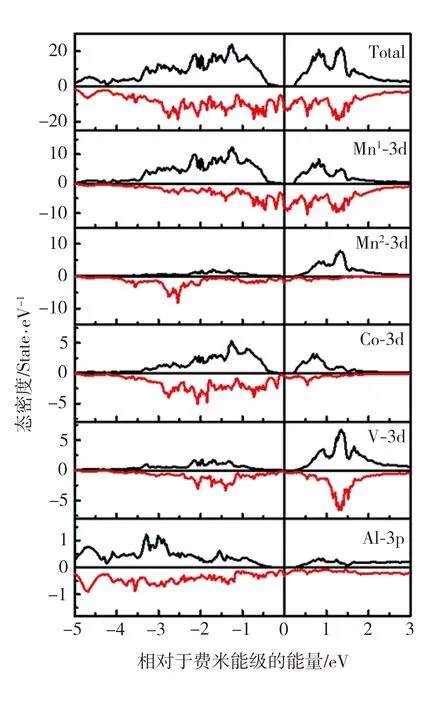
图5 Mn2V0.5Co0.5Al合金的总态密度图及各原子的分波态密度图

对Mn2V0.5Co0.5Al合金的理想有序结构进行弛豫优化，静态计算后得到相应的磁矩、极化率及形成能随晶格常数的变化，如图6所示。由图6(a)可知，根据能量最小化原则，得到平衡晶格常数为0.5747 nm；如图6(b)所示，当晶格常数在0.55～0.59 nm范围时，晶胞磁矩接近0 μB/f.u.，当晶格常数超过0.59 nm时，晶胞磁矩不为零，其完全补偿性遭到破坏；由图6(c)可知，当晶格常数在0.57～0.59 nm范围，合金仍保持完全自旋极化率，具有良好的半金属性；当晶格常数小于0.57 nm时，合金极化小幅降低；当晶格常数大于0.59 nm时，合金极化率变化较大，晶体磁矩完全补偿性和半金属性遭到破坏。

(a)形成能

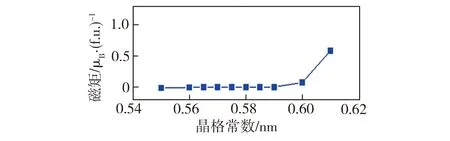
(b)磁矩

(c)极化率

3 结语

本文在三元Heusler合金Mn2VAl的基础上掺杂Co原子，形成Mn2V0.5Co0.5Al四元合金，基于密度泛函理论的第一性原理方法，对合金的电子结构、磁性和半金属性进行模拟计算。结果显示，Co原子的掺入能抑制Mn2V0.5Co0.5Al四元合金体系B2无序结构的形成。掺杂后，四元合金Mn2V0.5Co0.5Al具有完全自旋极化率(100%)，直接带隙宽度约为0.167 eV。Mn1、Mn2、Co、V不同原子的分波态密度图显示了不同程度的不对称性，在相同的能量附近原子轨道产生相互杂化作用，晶胞整体磁矩得到完全性的补偿(0 μB/f.u.)，并且Mn1、Mn2、Co、V的原子磁矩保持较高值(1.415、-2.801、-0.650、-0.763 μB)。四元合金Mn2V0.5Co0.5Al的优化晶格常数为0.5747 nm，当晶格常数在0.55～0.59 nm范围，晶胞磁矩接近为0 μB/f.u.，当晶格常数超过0.59 nm时，合金半金属性易遭到破坏。由此可见，Mn2V0.5Co0.5Al合金在晶格常数0.57～0.59 nm范围内具有良好的半金属性,磁矩能保持完全补偿。