裂纹磁悬浮双转子系统动态响应研究
王念先,刘明政,葛萍萍,姚俊夫
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
为获取高效率和高推重比,燃气轮机、涡轮机和航空发动机等旋转机械的核心转子部件广泛采用双转子结构。主动磁悬浮轴承(active magnetic bearing, AMB)具有无机械摩擦、无磨损、无需润滑、功耗低和寿命长等优点,用AMB取代支承双转子系统的机械轴承,即构成磁悬浮双转子系统,可显著降低系统复杂度,减轻质量,优化结构,大幅提升系统的可靠性、可维护性及整体性能[1]。在转子系统运行过程中,转子出现裂纹是常见故障,可能导致灾难性的后果。由于磁悬浮双转子系统具有复杂的耦合特性,同时存在内、外转子的多频激励,裂纹对系统的影响更为复杂[2],需要开展针对性研究。
裂纹转子的动力学问题已受到研究人员的广泛重视。Mayes等[3]通过一种余弦函数来考虑裂纹的呼吸效应。AL-Shudeifat[4]提出一种新的函数形式,可以更精确地描述裂纹的呼吸过程。Peng等[5]在时域内分析了裂纹位置对涡轮机械系统的涡动动力学影响,并将裂纹的呼吸函数改进为一个高次谐波。Wang等[6]提出一个同时考虑呼吸裂纹时变刚度特性和滑动轴承各向异性的模型,并研究了由轴承各向异性和速度相关特性引起的裂纹转子-轴承系统的动态稳定性。这些研究发现,裂纹可以与其他非线性特性耦合,影响转子系统的动态响应和稳定性,利用所提出的模型可以准确地分析裂纹转子的动态响应。
由于中介轴承的存在,双转子系统的内转子和外转子的动态响应存在直接耦合,双转子系统与单转子系统对裂纹的响应有很大差异。路振勇等[7]重点研究了空心轴中存在横向裂纹的双转子系统的非线性响应特性,指出裂纹能激发转子系统的超谐响应,但该双转子系统采用的是传统机械轴承。
除了传统裂纹转子系统的动态响应之外,研究人员对裂纹磁悬浮单转子系统的动态响应也进行了探讨。Zhu等[8]研究表明,与传统裂纹转子系统相比,含磁轴承的裂纹转子系统的动态特性更为复杂。钟志贤等[9]讨论了主动磁悬浮轴承的控制算法和控制器参数对有裂纹故障的Jeffcott转子系统动力学行为的影响。目前还未见对于含裂纹故障的磁悬浮双转子系统的相关研究报道。
为此,本文针对裂纹磁悬浮双转子系统的动态响应展开研究,采用有限元法建立系统动力学模型,同时采用PID控制策略,分析系统在不同控制参数下的动态特性,以期为磁悬浮双转子系统的建模和裂纹故障诊断提供参考。
1 磁悬浮双转子系统动力学模型
根据发动机双转子系统的结构特点,设计了一种相似的磁悬浮双转子结构,如图1所示,其中2个同轴转子通过机械中介轴承连接,转子由3个主动磁悬浮轴承(AMB1~AMB3)支承,AMB1和AMB2放置在内转子的端部,AMB3放置在靠近AMB1的外转子的端部。在裂纹动力响应研究中,由于双转子系统轴向自由度与径向振动之间的耦合可以忽略,因此这里不考虑系统的轴向自由度。
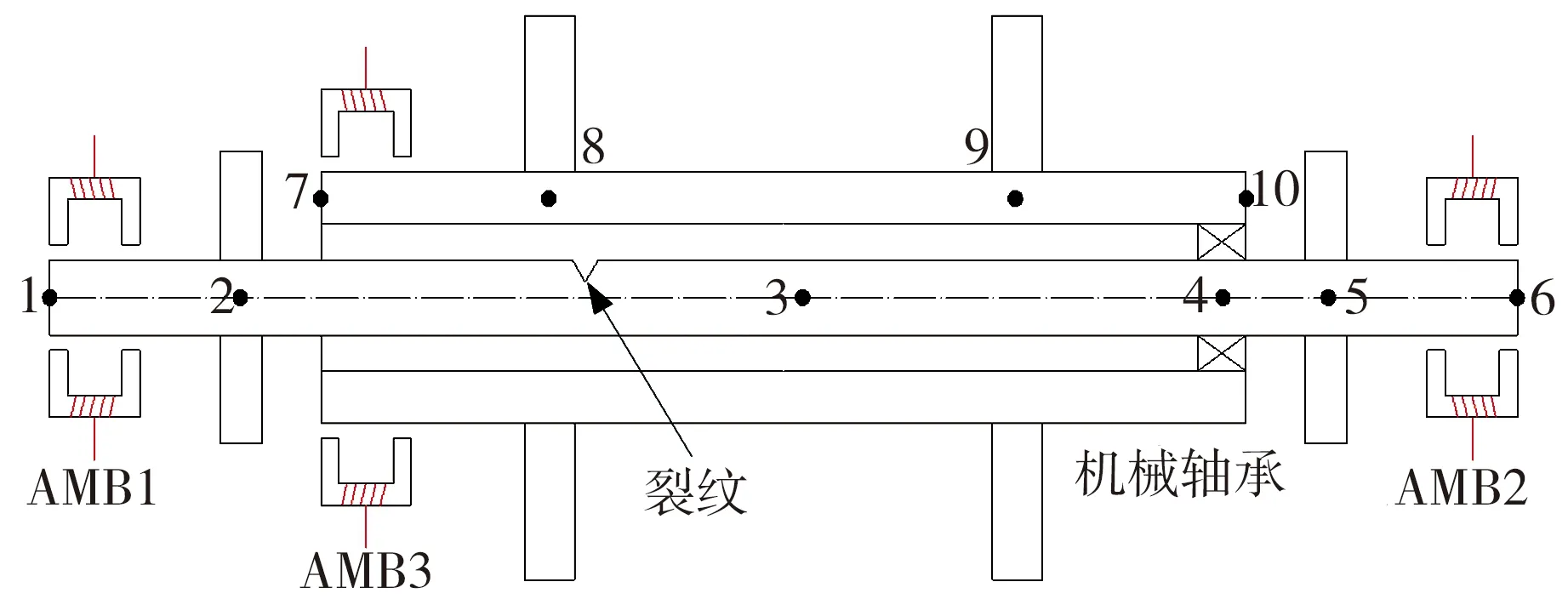
图1 裂纹磁悬浮双转子系统模型
采用有限元法对转子系统进行研究,将双转子系统分为8个轴段,共10个节点,转子系统的结构参数见表1和表2。
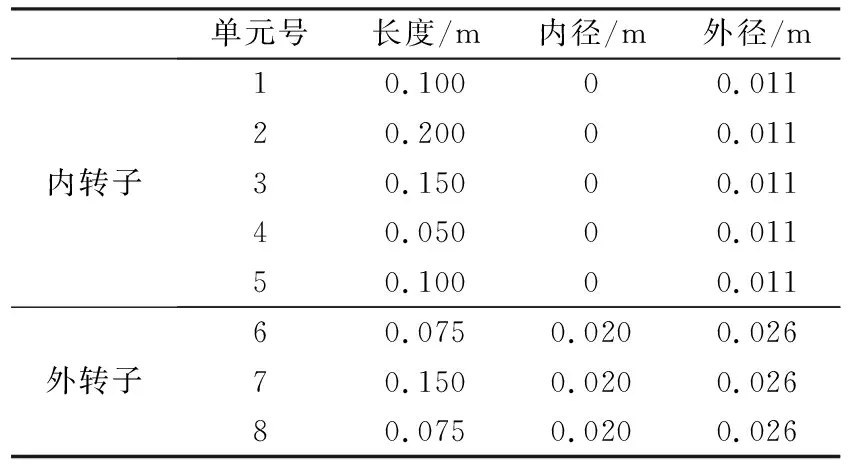
表1 系统各轴段的结构参数
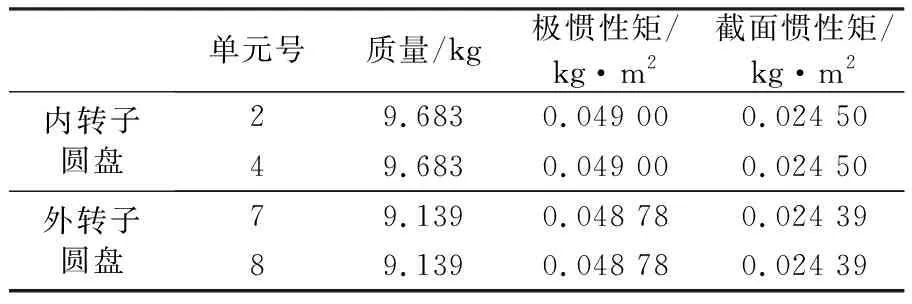
表2 转子圆盘的结构参数
1.1 圆盘动力学模型
磁悬浮双转子系统包含4个圆盘。假设圆盘是刚体,具有4个自由度,则圆盘在节点i处的运动方程如下:
(1)
其中,
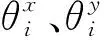
1.2 磁轴承动力学模型
与机械轴承类似,本文采用等效刚度和等效阻尼对磁轴承的支承特性进行描述。忽略磁轴承的漏磁和磁饱和等非线性特性,在PID算法控制下,磁轴承的等效刚度ke和等效阻尼ce可以描述为[10]:
(2)
式中:KP、KI和KD分别为比例系数、积分系数和微分系数;f为系统的涡动频率;Aa为功率放大器增益;As为传感器增益;ki和ks分别为磁轴承的电流刚度和位移刚度。
式(2)表明,等效刚度和等效阻尼不仅取决于磁悬浮轴承的结构和尺寸,还取决于控制系统和涡动频率。考虑到磁悬浮轴承在x、y轴上的弱耦合效应,忽略等效交叉刚度和等效交叉阻尼。这样一来,磁悬浮轴承就相当于2个相互垂直的弹簧阻尼结构。
假设磁悬浮轴承放置在节点i处,轴承的运动方程与圆盘具有相同的状态向量,可表示为:
(3)
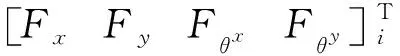
与磁悬浮轴承类似,中介轴承的动力学方程也可以表示为式(3)的形式,但其刚度和阻尼为定值。
1.3 转子系统动力学模型
采用有限元法建立转子的动力学模型,将转子分成N段和N+1个节点,基于Timoshenko梁单元,转子的动力学模型为:
(4)
将各刚性圆盘和轴承添加到选定的节点上,其质量和转动惯量矩阵被添加到相应的转子质量和陀螺矩阵中。中介轴承的添加过程稍有区别,它是内转子与外转子之间的一种支承,内、外转子在中介轴承处存在耦合。在该模型中,中介轴承放置在节点4和节点10之间,将轴承刚度矩阵加到转子刚度矩阵的元素K(13∶16,13∶16)和K(37∶40,37∶40)中。同时,要实现节点4和节点10之间的解耦,需在矩阵元素K(13,37)、K(37,13)、K(14,38)和K(38,14)处减掉中介轴承的刚度。对阻尼矩阵进行同样的运算即可获得双转子系统的动力学模型。
1.4 裂纹模型
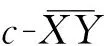
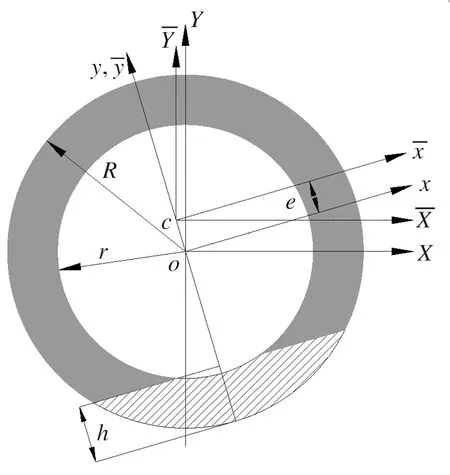
图2 裂纹转子横截面示意图
采用余弦函数对裂纹的呼吸过程进行描述[3]:
(5)
式中:f(t)为裂纹呼吸模型,表示裂纹随转子转速的变化过程。
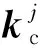
(6)
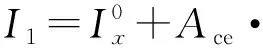
当裂纹较浅时(R-h>r):
sin-1(1-μr)]
(7)
3sin-1(γ)]
(8)
Ace=R2[π-cos-1(1-μr)+(1-μr)γ]-πr2
(9)
(10)
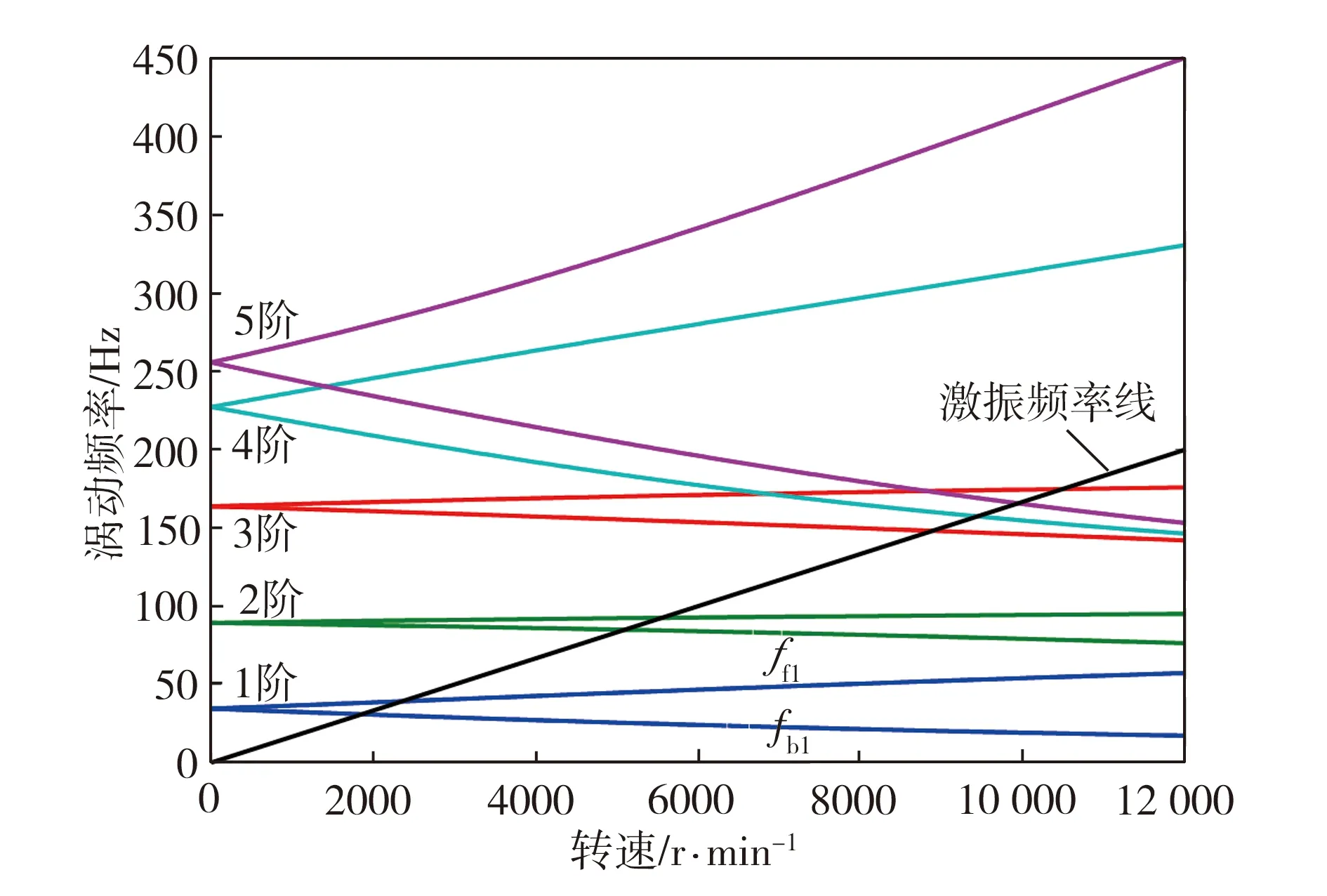
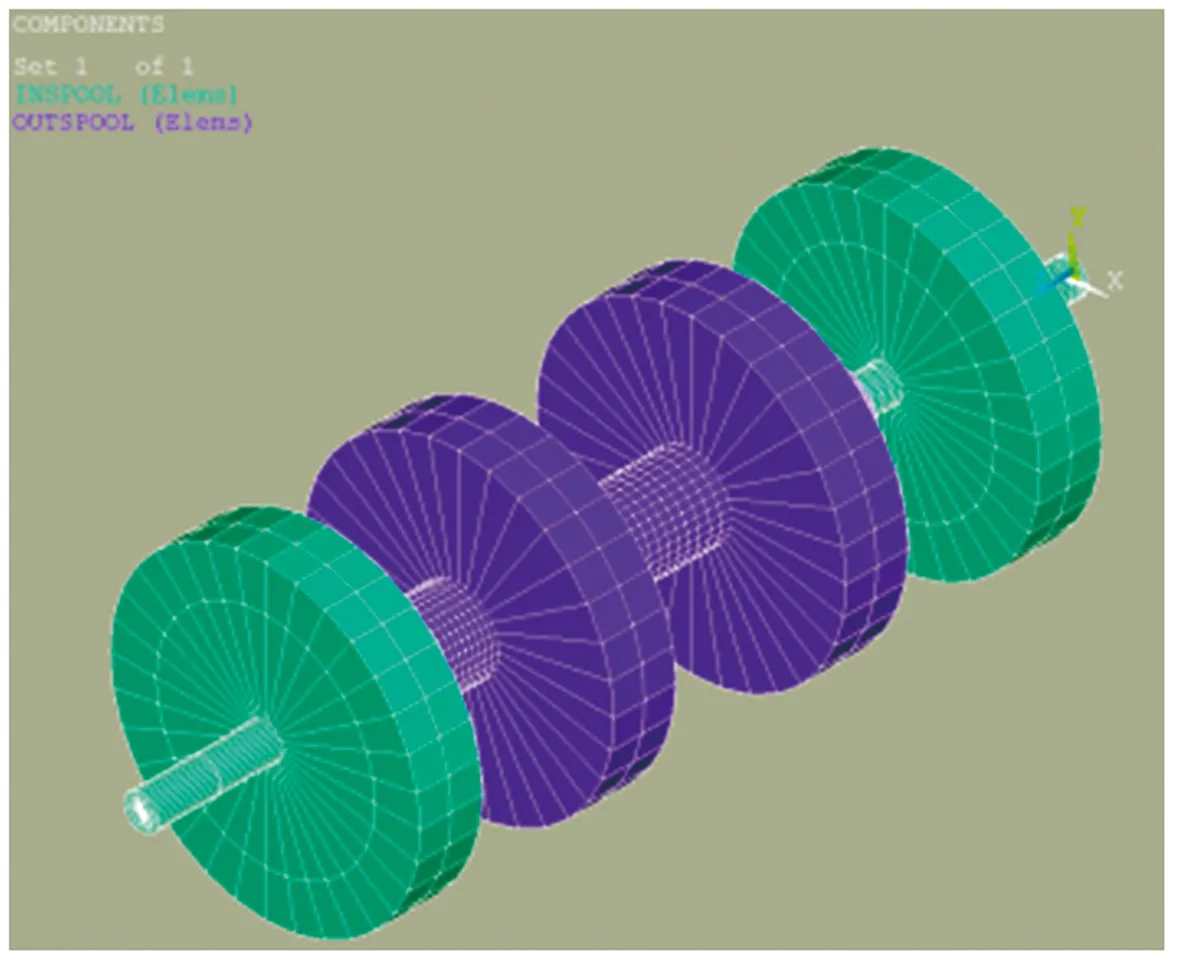
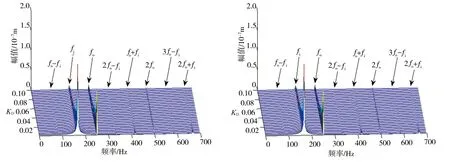
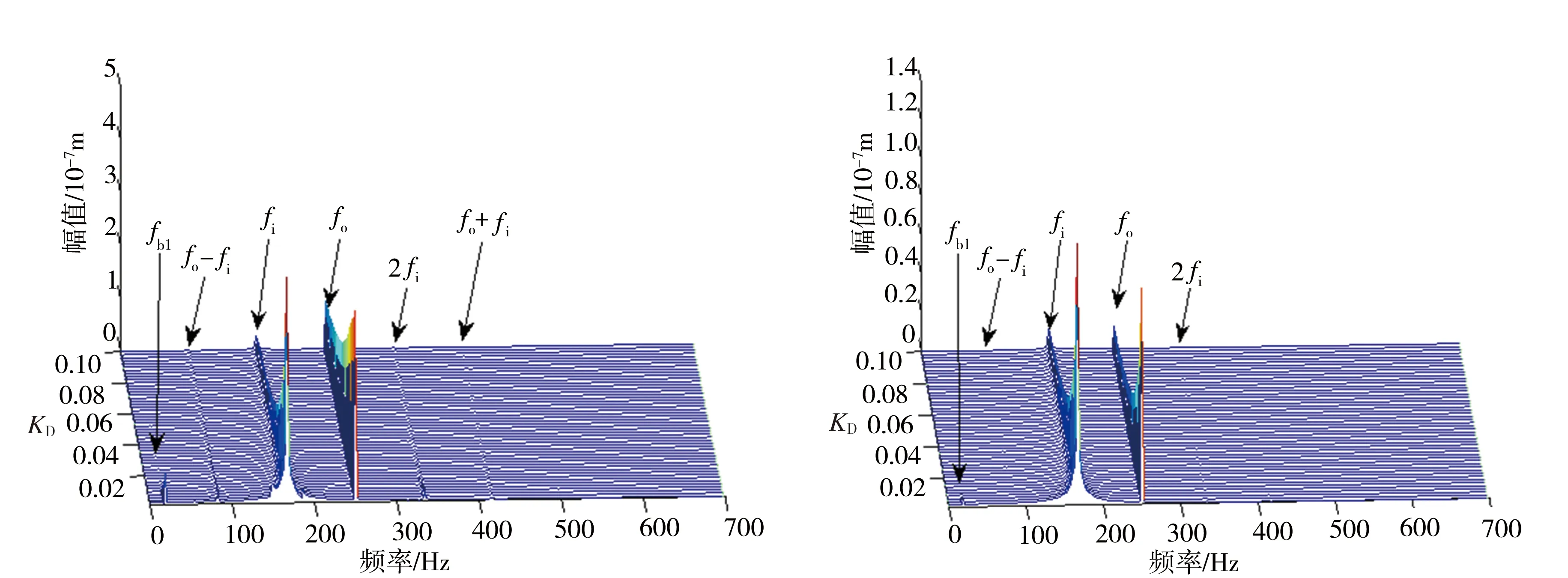
当裂纹较深时(R-h (11) (12) Ace=R2[π-cos-1(1-μr)+(1-μr)γ]- (13) α1=2cos-1[(R-h)/r] 因此,第j段转子产生裂纹时,裂纹单元新的刚度矩阵可表示为: (16) 式中:kj为第j段转子无裂纹时的刚度矩阵。 至此,裂纹双转子系统的动力学模型可表示为: =Fu(t)+Fg (17) 式中:Kc为裂纹刚度矩阵。 内转子激励下磁悬浮双转子系统的坎贝尔图如图3所示,从中可以得出转子系统的临界转速和前、后向涡动频率。图3中ff1和fb1分别为一阶前向涡动频率和一阶后向涡动频率。 图3 磁悬浮双转子系统的坎贝尔图 本文利用有限元软件对理论计算结果的准确性进行了验证,磁悬浮双转子系统的有限元模型如图4所示,结果对比如表3所示。 图4 磁悬浮双转子系统有限元模型 由表3可知,与有限元分析结果相比,解析模型对1阶临界转速的计算结果精度较高,2、3阶临界转速计算结果误差稍大,但总体上能满足理论分析的需求。 表3 解析模型的精度验证 采用Newmark-β法分析磁悬浮双转子系统的稳态不平衡响应。以靠近中介轴承的AMB2和AMB3的位移信号为对象,分别研究了内转子和外转子的振动。 当KP=20、KI=0.001、KD=0.05、内外转子转速比rs=1.5、内转子转速Ωi=10 000 r/min、μr=0.4时,AMB2处在不同裂纹条件下的时域响应、轴心轨迹和频率响应如图5所示。图5(a)为无裂纹转子系统的响应,图5(b)为外转子节点8和9之间出现裂纹时转子系统的响应,图5(c)为内转子节点3和4之间出现裂纹时转子系统的响应。 由图5可以看出,裂纹发生后,AMB2处的位移响应发生了明显的变化。裂纹会激发内、外转子的高阶谐波和叠加频率。在图5(a)中,没有裂纹时,AMB2的振动频率仅包括内转子的旋转频率fi和外转子的旋转频率fo。在图5(b)中,当外转子出现裂纹时,除了fi和fo外,振动频率还包含转子转速的倍频和内、外转子频率的叠加,可描述为nfo、nfo-fi和nfo+fi。在图5(c)中,当内转子出现裂纹时,AMB2的振动频率也发生变化,但与图5(b)不同的是,振动频率的分量主要由nfi、fo-fi和fo+fi组成。同样的情况也发生在外转子的AMB3中。 (a)无裂纹 (b)外转子裂纹 (c)内转子裂纹 保持系统运行参数不变,在外转子出现裂纹时,不同裂纹深度下AMB2和AMB3处的频率响应瀑布图如图6所示,可以看出,裂纹深度对磁悬浮双转子系统的频响特性有较明显的影响。在裂纹产生的初始阶段,除转动频率外,其他高阶谐波和叠加频率并不明显;随着裂纹深度的增加(μr>0.1),系统响应的频率分量逐渐变得复杂,更多倍频和组合频率被激发出来;当裂纹深度增加到一定程度时(μr=0.4),不会再激发新的频率成分。当内转子出现裂纹时,系统响应有相似的规律,这里不再赘述。 (a)AMB2 (b)AMB3 根据式(2),磁轴承的支承特性不仅取决于其结构和尺寸,还取决于控制参数KP、KD和KI,下面分析控制参数对裂纹磁悬浮双转子系统动态响应的影响。 保持系统运行参数不变,在不同KP取值下,内、外转子出现裂纹时磁悬浮双转子系统的频率响应瀑布图如图7所示,其中,图7(a)和图7(b)分别是裂纹位于外转子时AMB2和AMB3处的频率响应,图7(c)和图7(d)是裂纹位于内转子时同一位置的频率响应。 从图7可以看出,当裂纹位于外转子时,KP的变化对系统响应的频率分量几乎没有影响;但内转子出现裂纹时,频率分量随KP的变化产生了较明显的变化。在图7(c)和图7(d)中,当KP较小时,系统频率响应分量保持不变,但是当KP增加到一定程度后,频率响应分量中出现了一阶后向涡动频率fb1。 (a)AMB 2(裂纹位于外转子) (b)AMB 3(裂纹位于外转子) (c)AMB 2(裂纹位于内转子) (d)AMB 3(裂纹位于内转子) 由此可以得出结论,KP对系统频率响应的影响主要体现在裂纹位于内转子的情况下。当KP较大时,内转子裂纹会激发一阶后向涡动频率,而在相同条件下,外转子裂纹不会激发该频率。 保持系统运行参数不变,不同KD取值下,内、外转子出现裂纹时磁悬浮双转子系统的频率响应瀑布图如图8所示,其中,图8(a)和图8(b)分别是裂纹位于外转子时AMB2和AMB3处的频率响应,图8(c)和图8(d)是裂纹位于内转子时同一位置的频率响应。 从图8可以看出,与参数KP相比,KD对频率响应的影响更为严重。KD较小时,各频率分量的振动幅值较大;随着KD的增加,各频率分量的响应幅度迅速衰减;当内转子产生裂纹时,转子系统在KD较小时激发明显的一阶后向涡动频率fb1,fb1分量随KD的增加而消失。因此,增加KD值可以有效抑制转子频率响应中各频率分量的幅值,在KD较小的情况下,内转子裂纹会激发后向涡动频率。 (a)AMB 2(裂纹位于外转子) (b)AMB 3(裂纹位于外转子) (c)AMB 2(裂纹位于内转子) (d)AMB 3(裂纹位于内转子) 另外,根据式(2),KI对系统阻尼有影响,但主要体现在低频段,高频段可以忽略,研究结果将不在这里展示。 综上所述,KP和KD值会影响裂纹双转子系统的频率响应,特别是KP较大或KD较小时,内转子有裂纹时的系统频率响应中会出现一阶后向涡动频率fb1,而在相同条件下,外转子裂纹不会激发该频率,此特征可用于判断转子系统裂纹故障产生的位置。 本文研究了带有横向呼吸裂纹的磁悬浮双转子系统的动态响应特性。建立了裂纹双转子系统的有限元模型,并采用Newmark-β法得到系统的稳态不平衡响应,分析了不同裂纹情况下系统的时域响应、轴心轨迹和频率响应,讨论了控制参数对系统动态响应的影响。研究表明,裂纹可激发内、外转子的高阶谐波和叠加频率;当裂纹位于一个转子时,产生的高阶谐波和叠加频率在另一个转子上也可以观察到。控制参数会影响裂纹转子的响应,但产生的影响与裂纹出现的位置有关,当KP较大或KD较小时,内转子裂纹会激发出系统的一阶后向涡动频率,但在相同条件下外转子裂纹不会激发该频率。本文研究结果对磁悬浮双转子系统的裂纹建模和故障诊断具有一定的参考价值。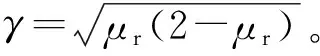
2 裂纹磁悬浮双转子系统的动态响应
3 控制参数对裂纹磁悬浮双转子系统动态响应的影响
3.1 KP对系统动态响应的影响
3.2 KD对系统动态响应的影响
4 结语

