基于特殊准随机结构模型的顺磁性奥氏体相的第一性原理研究

胡宇豪，魏 然，侯廷平，林恒福，王红鸿，吴开明

(1. 武汉科技大学省部共建耐火材料与冶金国家重点实验室，湖北 武汉，430081；2. 武汉科技大学高性能钢铁材料及其应用省部共建协同创新中心，湖北 武汉，430081；3. 武汉科技大学理学院，湖北 武汉，430065)

常温常压下铁的基态是铁磁性bcc相，当温度升高至超过居里点时，其转变成顺磁性bcc相，继续升高温度则转变为顺磁性fcc相，即奥氏体相[1-2]。奥氏体相作为高温相，有一些基本物理参数不容易直接通过实验获得。目前，普遍采用的计算方法是基于密度泛函理论的第一性原理，其主要用于研究多电子体系结构，适用于基态和0 K、0 Pa条件下材料微观物理参数的计算。

已有研究表明，fcc Fe的基态是双层反铁磁结构[3-5]，但奥氏体在工作状态是顺磁性结构。顺磁性结构磁性弱、磁矩分布复杂，研究时普遍将其视作无磁性结构来处理，即不考虑自旋极化。顺磁性实质是体系中某原子或基团含有没有完全抵消的磁矩，而磁矩之间的相互作用远小于热动能，故磁矩整体呈现无序排列状态，使材料不能形成自发磁化。由此看来，若采用忽略自旋极化作用的方式来模拟顺磁性fcc结构，则会影响材料参数计算结果的准确性[6]。而传统的第一性原理计算方法适用于研究周期性结构，无法构建奥氏体相的顺磁性结构。

特殊准随机结构(Special quasi-random structure，SQS)模型最早由Zunger等[7]提出，最初应用于计算半导体和过渡金属合金的热力学和光学性质等[8-9]。该方法的基本思想是，在一定大小超晶胞下，找到一个特殊构型，通过匹配团簇关联函数找到最接近随机的构型。由于其计算量较小，目前已替代传统构造超原胞结构的方法，广泛应用于模拟随机合金系统和固溶体。基于此，本文采用SQS构建顺磁性奥氏体相，计算了奥氏体相的晶格常数、磁矩和空位形成能，并与其他方法计算结果及实验值进行对比。

1 模型与计算方法

将顺磁性奥氏体相视作原子配比为1∶1的AB型化合物，其中A表示自旋向上的Fe原子，B表示自旋向下的Fe原子。本文用于模拟顺磁性奥氏体相的SQS结构单胞含有16个Fe原子，各原子的分数坐标见表1，SQS-16(A8B8)b结构示意图如图1所示，箭头方向表示原子的自旋方向。

图1 顺磁性fcc Fe结构示意图

表1 SQS fcc 8/8分数坐标

本文所使用的计算方法是基于密度泛函理论的第一性原理，通过VASP软件实现对结构弛豫和能量的模拟计算。收敛性测试结果显示，520 eV是获取高精度能量差的一个充分截止点，能量收敛精度为10-5eV/atom。交换关联能量泛函

采用改进的广义梯度近似(GGA)和PBE赝势来处理，离子-电子交互作用采用投影缀加平面波方法(PAW)。

本文模拟顺磁性奥氏体相时所使用的原胞如图1所示，模拟无磁性奥氏体相所使用的原胞为含有4个Fe原子的fcc单胞。为了减少空位浓度对计算结果的影响，无磁性和顺磁性fcc Fe相计算中使用的晶胞均为含64个Fe原子的超胞，晶胞规格与对应布里渊区k点网格设置如表2所示，其中a表示晶格常数。分别计算完整晶胞和去除一个原子后的晶胞(含单个空位)的平衡态总能量和平衡体积，使用B-M(Birch-Murnaghan)状态方程(Equation of state，EOS)拟合得到fcc Fe的平衡晶格常数，通过式(1)计算得到fcc Fe空位形成能[10]：

表2 晶胞结构参数和k-points设置

(1)

式中：E(N)和E(N-1)分别代表N和N-1个原子组成的经过充分弛豫的超胞总能量。

2 结果与讨论

2.1 结构的能量-体积曲线及磁矩

由于SQS单胞没有对称性，是一种亚稳态结构，其结构优化步骤比普通的对称结构要复杂，故本文共分3步进行优化：首先，通过不断改变POSCAR文件中缩放系数来获取不同的SQS超胞的体积，仅作电子态的自洽计算，使用B-M状态方程拟合得到随超胞体积变化的能量-体积(E-V)曲线，并找到能量最低点对应的体积V1；随后，在V1上下5%的范围内找到等体积差距的9个点(含V1)，对其形状进行固定，改变原子位置的弛豫(ISIF=2)，离子弛豫到平衡位置后再进行电子态的自洽计算，拟合得到E-V曲线；最后，进行既改变形状又改变原子位置的弛豫(ISIF=4)操作，离子弛豫到平衡位置后，静态计算体积V及对应的能量值E，再次拟合得到E-V曲线。SQS原胞结构优化前后的E-V关系曲线如图2所示。由图2可见，体系的总能量随着体积的变化先收敛至一定值，随后继续增大，并且随着三次优化步骤的不断进行，体系收敛总能量逐渐降低，体系更加稳定。

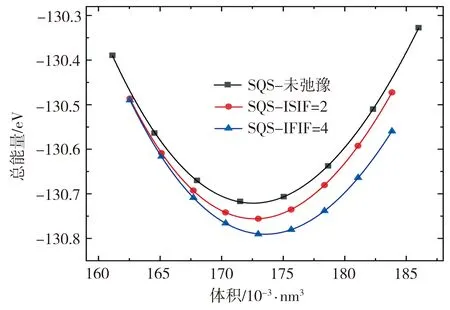
图2 优化前后SQS结构的E-V曲线

对顺磁性和无磁性fcc Fe结构进行能量散点计算，两种磁性结构优化后E-V曲线如图3所示。由图3可见，当处于平衡态时，相比于无磁性fcc Fe结构，顺磁性结构的总能量更低，结构更加稳定，由此可以得到完全弛豫后结构的平衡态总能量、晶格常数等基态性质。

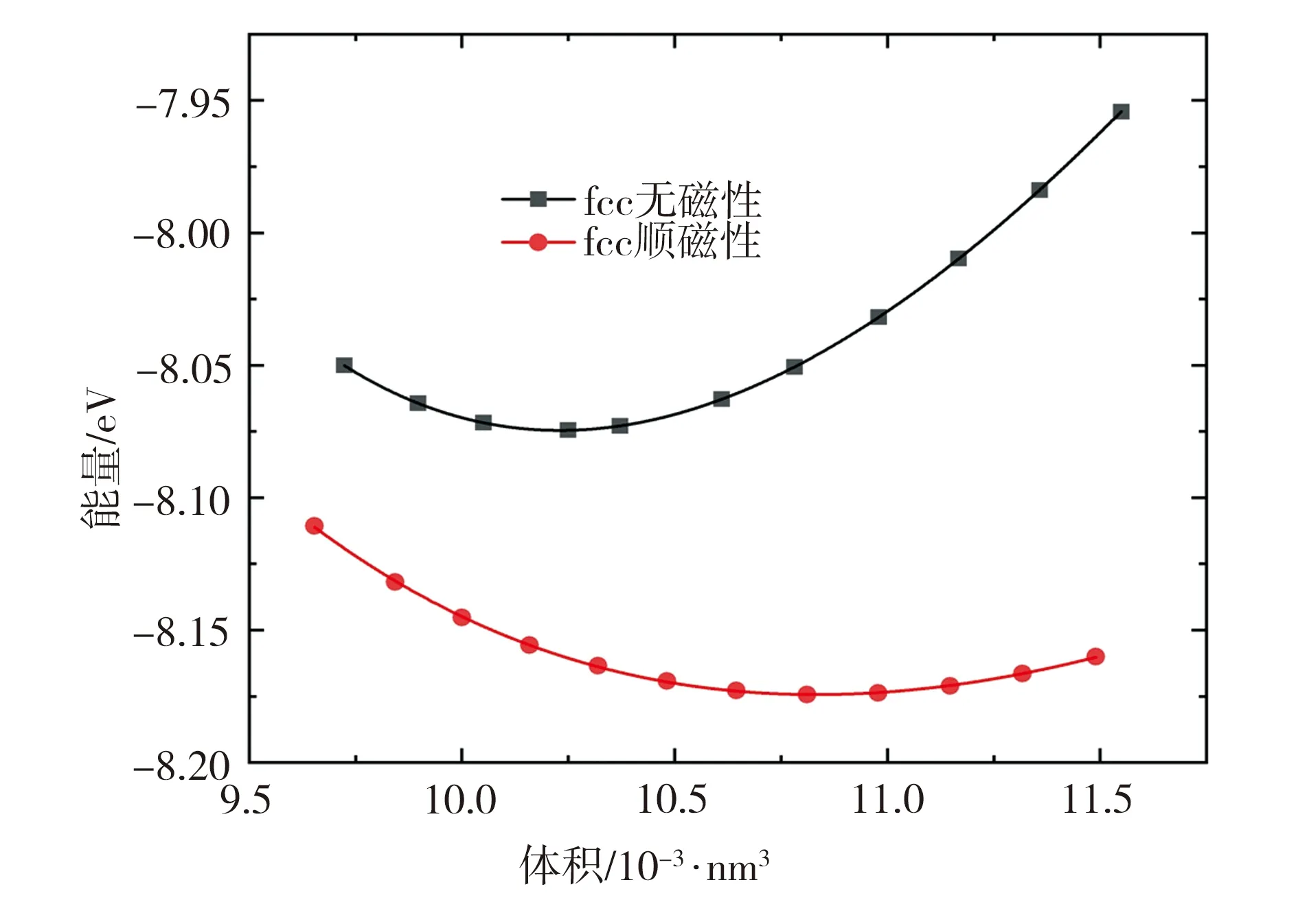
图3 完全弛豫后fcc Fe结构的E-V曲线(ISIF=4)

顺磁性和无磁性fcc Fe结构中各原子磁矩随体积变化如图4所示。由图4可见，顺磁性结构的体积-磁矩曲线中，Fe原子的磁矩在0.75～2.0 μB之间，属于正常范围[11]；其中单个Fe原子的磁矩随晶胞体积的增大而缓慢增加，这是由于随着晶胞体积的增大，Fe晶胞结构电子密度减小，有利于自旋平行，但总磁矩仍基本保持为0，结构保持顺磁特性[12]。

图4 顺磁性(SQS)和无磁性fcc Fe结构的磁矩随体积的变化

2.2 晶格常数

表3列出了本文模拟计算得到顺磁性和无磁性fcc Fe的平衡晶格常数以及文献中报道的实验值和模拟计算值，其中文献[13]中报道的是利用Ackland赝势基于分子动力学计算得到的结果，文献[11,14]则分别是模拟无磁性和低自旋反铁磁性后通过第一性原理计算得到的结果。由表3可见，无磁性fcc Fe结构的晶格常数计算结果与文献[11]和文献[14]计算结果吻合较好，但与实验测定值差别较大，偏差分别为3.26%和3.07%，而顺磁性奥氏体相的模拟计算结果与实验值的偏差相对较小，仅为1.49%和1.29%。由此可以看出，顺磁性状态fcc Fe的模拟结果明显与实验测定值一致性更好，表明无磁性状态模拟方法不能准确地反映奥氏体相的基态性质，而通过SQS模型模拟顺磁性奥氏体相是可行的。另外，顺磁性fcc Fe相平衡晶格常数的计算结果要略大于无磁性fcc Fe相的相应值，这是由于磁致伸缩作用所导致的[17]。

表3 不同方法所得fcc Fe的晶格常数

2.3 空位形成能

表4为本文模拟计算得到fcc Fe的空位形成能(完全弛豫)以及文献中报道的结果，其中文献[19]是基于正电子湮灭技术通过空位-能量理论模型得到的计算值，文献[20]则是基于第一性原理计算得到铁磁性fcc Fe的空位形成能。由表4可见，本文计算值和文献中报道的基于第一性原理的计算结果均略大于实验值，这是由于奥氏体工作状态是高温态，而第一性原理只能计算0 K、0 Pa下基态的性质。此外，本文计算得到顺磁性fcc Fe结构的空位形成能更接近于实验值和前人的计算结果，偏差相对较小。由此可见，本文采用SQS构建顺磁性奥氏体相方法能够较好地模拟奥氏体基态性质，结合第一性原理能模拟计算得到较准确的奥氏体相的晶格常数和空位形成能，该方法的有效性得到验证。

表4 fcc Fe结构的空位形成能

3 结论

为探究将特殊准随机结构(SQS)模型应用于模拟顺磁性物质的可行性，本文利用SQS构建顺磁性奥氏体相，基于第一性原理计算得到顺磁性和无磁性奥氏体相的平衡晶格常数和空位形成能，并将优化后两种磁性结构的计算值与实验值和前人的计算值进行对比。结果表明，相较于无磁性fcc Fe结构的模拟计算结果，利用SQS构建顺磁性奥氏体相模拟计算得到的平衡晶格常数和空位形成能均与实验值和前人计算结果有更好的一致性。由此看来，利用SQS模拟顺磁性奥氏体相并结合第一性原理的计算方法是可行的，这对于其他顺磁性结构的模拟计算工作具有一定的参考价值。