信息技术下的中学数学可视化教学*——以GeoGebra、几何画板辅助教学为例

广东省佛山市顺德区沙滘初级中学(528315) 钟小玲 黄金雄

数学的研究对象是抽象的,其学习过程也是一种抽象问题形象化、具体化的过程.特别是在呈现动点轨迹难题、函数的动态变化、图形的变换、几何模型时,如果能借助信息技术中的“可视化”技术,将数学的抽象性问题、学生看不见的思维过程、不可言说的思想方法等清晰的呈现出来,不仅有利于启发学生的思维、提高学生分析问题解决问题的能力,更有助于培育学生的数学核心素养.

GeoGebra 与几何画板是当代信息技术的集大成者,也是目前主流的动态数学软件.它们功能强大、交互性强,能将抽象的数学知识变得生动直观,易于理解.而且它们的版面简洁,易于操作,是中学数学课堂常用的辅助教学手段.本文结合具体的案例,论述它们在中学数学教学可视化教学的独特作用,为教师利用GeoGebra、几何画板辅助中学数学的可视化教学提供借鉴.

1 抽象问题形象化、具体化,突破动点轨迹难点

近年来,综合了函数,图形变换,方程等知识的动点轨迹问题颇受命题者的青睐,是中考的热点问题,也是难点问题.学生在解答此类问题时,常常不知所措,无从下手,究其原因是不能发现“动”之中的“静”,抓不住问题的本质.而GeoGebra 与几何画板凭其强大的功能,化繁为简,化动为静,是解决此类问题的神助攻.

案例1:(2020 广东省中考第17 题)有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫、老鼠都理想化为同一平面内的线或点,模型如图,∠ABC=90°,点M、N分别在射线BA、BC上,MN长度始终不变,MN=4,E为MN的中点,点D到BA、BC的距离分别为4 和2.在此滑动过程中,猫与老鼠的距离DE的最小值为____.

GeoGebra 动态演示

案例2:(2020 佛山市顺德区中考模拟)如图,抛物线y=-x2+2x+3 与x轴交于A、B两点,顶点为D,对称轴交x轴于点E,点P为对称轴上一点.以BP为边在BP的下方作等边三角形ΔBPQ,当点P从点D运动到点E的过程中,求出点Q经过的路径的长度是多少?

原图

几何画板追踪点的运动轨迹

案例3:(2018 南通市中考)如图,正方形ABCD中,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.求线段OF的最小值.

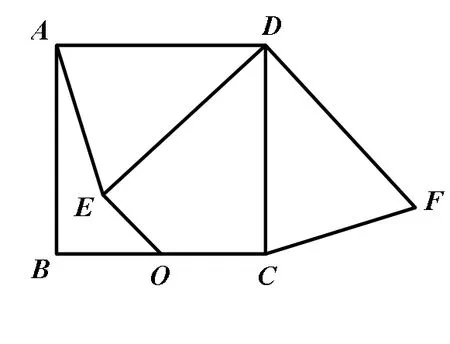
原图

几何画板动画演示图

上述案例都是动点问题,大部分学生看到此类问题,第一反应就是迷茫,无从下手.上述图形都会随着点的运动发生改变,学生若在平时的学习中没有学会抓住“主动点”,理清“从动点”,找出动点的轨迹,那必然不会解决此类问题.

而这种动态问题就是我们数学教学的重难点,如何将“动”化为“静”,抓住本质,这时GeoGebra 与几何画板就是我们的教学神器,我们可以借助它们追踪点的功能,将运动轨迹形象直观的展示给学生看,同时引导学生发现此类题目的本质.而这也达到了我们教学可视化的目标之一,将学生看不见的思维过程、将不可言说的思想方法等清晰的呈现出来,从而提升学生分析问题解决问题的能力.

2 趣味盎然,简明易懂,激发学生学习的内驱力

脑科学研究表明,人类80%以上的信息是通过视觉获得的,常言道“一图胜千言”,因此抽象的知识可视化显得尤为重要.数学历来以其高度的抽象性、严密的逻辑性被人们所赏识,然而也恰恰是这点,令很多学生望而生畏.教师在教学中将抽象晦涩的数学知识生动形象的展示出来,让学生感受到数学的简单、对称、无限、和谐的美,在数学学习中起着至关重要的作用,而借助GeoGebra 与几何画板不单能有效激发学生学习兴趣,同时可以将一些抽象的定理通过动态图形的演示,简洁易懂,激发学生学习的内驱力.

案例4:利用几何画板中的绘图、深度迭代和参数功能,可以绘制出一棵五彩斑斓,动态生长的勾股树.点击“生长”、“颜色变幻”按钮,树就开始动态变化,十分美丽.

“面动成体”动画演示

案例5:利用几何画板中的绘图、点的追踪、动画等功能,可以将“面动成体”的过程形象生动的演示给学生看,加深学生对概念的理解.每每播放这个课件,学生总会发出兴奋的惊呼声.

案例6:利用GeoGebra 制作动态图形,形象生动的演示勾股定理的证明.

图1 至图4,直角三角形都是可以移动的,点击动画,学生能形象直观的观察到勾股定理a2+b2=c2.图5、图6 是动态演示的示意图,GeoGebra 以其强大的功能,让勾股定理“活”了起来.

图1

图2

图3

图4

图5

图6 达芬奇证明的动态演示

法国数学家笛卡尔说:“没有任何东西会比几何图形更能简单直接的引入脑海,用图形表达事物是很有帮助的.”上述案例不仅让学生感受到了数学图形的千姿百态的美,激发学生探索的欲望,更是将高深莫测的数学证明变得平易近人.当然我们不仅仅把数学的教学停留于视觉吸引这一浅层次的目标,我们还会关注更深层的目标,帮助学生把视觉感知到的外在物质工具内化为学生进行学习、研究问题的内在心理工具.

3 数形结合,生动形象,加强函数性质把握

数与形是中学数学研究的两大基本对象,数形结合就是将抽象的数量关系与直观的几何图形结合起来,建立对应关系,通过数与形的互相转化,达到“以数解形”、“以形助数”的效果.数形结合是一种非常重要的数学思想方法,贯穿于初中三年的数学教学.GeoGebra 与几何画板凭借其强大的功能,完美的将抽象的数量关系与直观的几何图形结合起来,帮助学生深刻的理解函数的相关知识,有效的提升学生数形结合的能力.

反比例函数图像

二次函数图像

案例8:探究二次函数y=a(x-h)2+k的图像分别随a,h,k变化的规律.利用几何画板的参数、函数绘制、动画等功能绘制出二次函数的图像,分别点击三个参数的动画按钮,学生能直观形象的观察到每一个参数变化带来的函数图像的变化,从而在头脑中形成一个整体、具体的印象.

案例9:利用GeoGebra 绘制反比例函数图像,并探究反比例函数相关的面积性质.

GeoGebra 动态演示面积相等的几种情形

运用信息技术使数学教学视觉化的目的之一,就是化数学的抽象为直观具体,使其利于学生观察,视觉感知,降低理解难度.而上述三个案例就很好的将抽象的函数直观化,动态化,加强了学生对知识的理解和把握.学生若在平时的学习当中,很好的把握了函数的性质,那么遇到相关的问题时就会得心应手.

4 一题多解,举一反三,提升学生数学思维水平

案例10:(2020 广东省中考第25 题)如图,抛物线与x轴交于点A、B,点A、B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为第(3)问:点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当ΔABD与ΔBPQ相似时,请直接写出所有满足条件的点Q的坐标.

原图

GeoGebra 绘制两种情况

案例11:如图,在正方形ABCD中,点E是BC边上一点,点F是BC延长线上一点,AE垂直与EG，EG交∠DCF的角平分线CG于点G,求证:AE=EG.

从上述两个案例可知,我们数学教学中常常需要启发学生思考解决问题的多种可能性.特别是第二个案例,我们希望学生能一题多解,思维发散,举一反三.而几何画板的构图思想,能激发学生在实际分析过程中不断拓展思维,触类旁通,发现解决问题的多种可能性.与此同时,利用GeoGebra与几何画板辅助我们的教学,有利于提升学生的思维水平,使其从浅层学习向深度化学习转化.

5 结语

总之,运用信息技术使数学教学可视化,能有效的突破动点轨迹难题,能帮助学生更好的理解性质,能让学生有效开展数学探究,提升学生的思维水平.GeoGebra 与几何画板作为辅助性教学手段在中学数学可视化教学中有着独特的作用,它们能够动态演示过程,揭示数形关系,突显研究对象间的内在联系,从而降低学生的认知负荷,优化学生的认知结构,提高教学的教学效率与教学质量.