从“动态量”与“不动量”的角度思考解析几何的定值问题

李悦 陶军

摘要：解析几何定值问题是几何中具有代表性的一类问题，同时也是学生解题的一个难点。正确审题并在限定的时间内找准方向，展开解答思路，是解答解析几何题目的关键。如何入手，如何设解，如何快速运算，最终在有限的时间内为完成整题的解答，有效的找准解题思路，找准切入点就尤为重要。

关键词：解析几何  定值问题  变量处理  数形结合

解析几何定值问题是几何中具有代表性的一类问题，其本质是研究几何图形中的不变关系。研究的方法是先特殊情形猜出定值，再进行严谨的推理证明。在解决问题的过程中，需要挖掘几何特征并对几何条件恰当地代数转化，而代数运算常常涉及多个变量的处理，对学生的综合能力要求比较高。选择恰当的变量，建立给定代数化的几何关系和目标所求之间的联系，这其中的核心便是研究对象间的位置关系，如果研究对象的位置关系确定了，就可以用代数的形式进行表达了;其次是对含字母的代数式进行运算和变形，需要不断分析给定关系和目标之间的联系，寻找运算的方向，选择灵活的计算途径，有效简化运算进行求解，需要较高的数学运算素养和逻辑推理素养。解析几何定值问题使学生经历“猜想证明”、“探索实践”“转化和化归”等问题研究的过程，锻炼了学生的猜想证明科学素养、由特殊到一般、数形结合的基本思想方法和能力。

本文通过一道题目的解析，从“动态量”与“不动量”的角度，通过研究对象的位置关系，分析建构选择合理变量的分析方法，由几何与代数的合理转化，表示目标解析式，根据目标寻找并优化计算方向等方法性知识，能够从整体上把握解题的主干思路和局部内恰当的选择运算方向，从而提升学生直观想象、数学运算和逻辑推理等数学核心素养，这也符合高考数学北京卷试题解析几何一贯秉持“多想少算”的理念，注重学生“动手尝试、探索实践”的能力和“先猜再证”的基本研究方法。

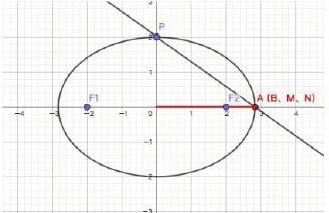
问题：已知椭圆C：   的上顶点为P，点A、B（A、B与点P都不重合）是椭圆C上关于 轴对称的两点，直线PA交 轴于点M，直线PB交 轴于点N，O为坐标原点，证明： 为定值。

环节一：猜想定值

分析：题中要求A、B为椭圆上不同于P的任意两点，那么当A、B在什么位置时， 最容易得出？学生容易想出的是椭圆与坐标轴的交点，由于A、B两点都不与点P重合，所以排除椭圆的下顶点。因此学生通过画图、观察可以找到椭圆的左右顶点处。

预设：点A位于椭圆的左顶点，B为点A关于 轴的对称点，此时B点与A点 重合，因此M点与N点重合。所以此时  ，因此可以猜想 为定值8。同时教师还需总结：什么是特殊位置，点的特殊位置一般选取与坐标轴的交点，直线的特殊位置一般为平行或者垂直的情况。在特殊位置猜想出结果，一般情况需推理证明。

环节二：推理证明

问题2：根据题意，通过画图的过程，请你分析图形中哪些量是动态的？哪些量是不动的（确定的）？

分析：学生绘图，在绘图的过程中再次理解题意，找到题目中的“动态量”和“确定量”。

确定量：椭圆方程已知，因此椭圆的轨迹是确定的;椭圆与坐标轴的交点坐标确定，即点P（0，2）是已知的;点A与点B的位置关系是确定。

动态量：由题意：点A、B是椭圆上与点P不重合的动点，可知直线PA、PB为動直线，进而两条直线分别与 轴的交点M、N的位置即为不确定，M、N的位置不确定，计算 就存在困难。

在解决解析几何问题时，学生往往是清楚基本方法的，即：（1）选择适当的变量。（2）进行代数运算，整理所求的目标。但题目中不确定的量有那么多，到底应该选择哪个变量是“适当”的变量呢？这恰恰是学生最困难的地方。这个困难突破的关键，是引导学生找到哪个变量是引起其他量改变的“源头”呢？找到了变化的“源头”，就可以抽丝剥茧，顺藤摸瓜，理清整个解题思路。

在研究平面解析几何问题时，要注重培养学生能够根据问题的条件，读出几何对象的几何特征的能力。在明确研究对象几何特征的基础上，再根据研究对象间确定的几何关系，合理的设出参变量，列出简易的思维简图：将几何元素的代数化、研究对象之间位置关系的代数化、所求的目标代数化。

综上所述，平面解析几何这门学科研究的对象是直线、圆和圆锥曲线;“动”与“不动”是理解平面解析几何问题的思维特征;研究几何对象的几何特征（性质与位置关系）是解决平面解析几何问题的一般方法。

北京市怀柔区第二中学   北京市怀柔区第一中学