基于神经网络的欠驱动水下机器人三维同步跟踪和镇定控制
方 凯,姚佳琪,李家旺
(宁波大学海运学院,浙江宁波 315211)
1 引言
近年来,水下机器人(autonomous underwater vehicle,AUV)在海洋资源开发、海底勘探和军事侦察等领域得到了越来越广泛的应用,也使得对其三维空间运动的控制技术的研究受到了越来越多的重视.对于AUV的运动控制问题,其主要难点在于一般情况下AUV都具有欠驱动特性,即AUV的独立控制输入数目少于其自由度数,由于不满足Brockett必要条件[1],因此无法通过连续时不变控制策略实现镇定.此外,AUV在实际工况下经常受到未知外界干扰、模型参数不确定性和输入饱和限制的影响,这些也使得AUV的三维运动控制变得更加困难.
目前,针对AUV的实时三维空间运动控制问题的研究主要可以分为2类:镇定控制与轨迹跟踪控制.在镇定控制问题中,需要选择合适的控制输入形式使得AUV的状态误差收敛到零或零点附近的有界邻域内.如文献[2-4]中基于四元数形式的6自由度欠驱动AUV模型,提出了一种连续周期时变控制律以实现位置和姿态角的局部指数镇定.其中文献[2-3]未考虑环境干扰的影响,最终使状态误差收敛到零点,而文献[4]考虑了环境干扰的影响,使控制误差收敛到零点的有界范围内.在该控制方法基础上,针对AUV的控制输入饱和限制,文献[5]中设计了基于模型预测控制的AUV镇定算法.然而,上述文献均未考虑大初始误差情况.与镇定控制问题不同,在轨迹跟踪控制问题中,需要设计控制策略使得AUV的状态趋近并跟上满足持续激励条件的时变轨迹,实现状态误差的收敛.如文献[6-7]针对欠驱动无人水下航行器的三维轨迹跟踪问题设计了一种基于虚拟速度误差变量的反步控制方法.文献[8]基于反步法设计了一种输出约束的三维跟踪控制方法.文献[9]提出了基于生物启发式速度调节方法的欠驱动AUV三维轨迹跟踪控制策略.但在上述4篇文献中,系统模型均假设为完全已知.针对模型参数不确定性和输入饱和限制情况,文献[10]中提出了欠驱动AUV的三维自适应轨迹跟踪控制方法,但其并未考虑外部干扰的影响.文献[11-12]分别通过自适应神经网络和比例积分微分(proportional integral derivative,PID)滑模控制方法解决参数不确定问题和外界干扰,但均未考虑输入饱和问题.
需要指出的是,在实际的AUV的三维空间工作任务中,其可能需要同时具备实现镇定控制和轨迹跟踪控制的能力,但上述提及的控制方法均无法达到.考虑到在任务过程中切换不同控制方法可能引起控制系统不稳定或失效,因此设计一种能够同步实现镇定和跟踪的控制策略对于AUV的技术应用十分有益.现有的同步镇定和跟踪控制方法主要应用于平面运动系统.如文献[13]中设计了一种统一控制方法以解决欠驱动船舶的同步镇定和跟踪控制问题,该方法也可应用于非完整移动机器人的相关控制问题[14-15].针对非完整移动机器人的运动学模型,文献[16]中基于Lyapunov理论和通过引入虚拟控制量设计出一种形式简单的统一控制器.然而,上述4篇文献中的控制方法均存在误差收敛速度较慢和对于初始误差较敏感等问题.针对这些问题,文献[17]基于动力学振荡器提出了一种统一控制方法,并针对欠驱动水面船的同步跟踪和调节问题进行了研究.文献[18-19]通过采用“横截函数”(transverse function)方法[20]设计了欠驱动船舶的同步跟踪和镇定控制策略.但是上述3篇文献均未考虑控制输入饱和限制的影响.针对受到模型参数不确定性影响和输入饱和限制作用下的欠驱动船舶,文献[21-22]中通过引入辅助控制项设计出一种统一控制策略以实现同步跟踪和镇定.
受到上述研究的启发,本文针对欠驱动AUV的三维同步跟踪和镇定控制问题开展了研究.在建立欠驱动AUV空间运动数学模型基础上,通过分析不同期望轨迹的特点,设计一种虚拟控制策略以实现对欠驱动方向的控制.结合反步法和Lyapunov直接法设计思想,并考虑AUV模型参数不确定性、未知干扰及输入饱和限制等影响,设计出一种饱和动力学控制器,使得AUV的误差状态能够收敛到零点附近的有界范围内.最后,通过数值仿真实验形式,对所设计控制策略的有效性进行验证.
2 问题描述
2.1 AUV模型
本文所研究的AUV是具有轴对称外形的刚体并配置有轴向、俯仰和偏航方向上的独立控制输入.忽略横滚运动的影响,则可得如下形式的5自由度AUV三维运动数学模型[23],由于系统控制输入少于其自由度数,故属于欠驱动系统.
1) 运动学模型:
2) 动力学模型:

其中:(x,y,z)表示地面固定坐标系中AUV的空间位置坐标;θ和ψ分别表示AUV的俯仰角和偏航角;(u,v,w)为随体运动坐标系中AUV的线速度,q和r分别表示AUV的俯仰和偏航角速度;mi >0(i=u,v,w,q,r)为包含附加质量的AUV惯性项;di >0(i=u,v,w,q,r)为AUV的水动力阻尼系数;W和分别表示AUV排水量和纵稳性高;τwi(i=u,v,w,q,r)表示包含模型参数不确定性和环境干扰影响的未知作用项;(τu,τq,τr)表示AUV的控制输入,考虑到AUV的实际控制输入都存在饱和限制,因此有

其中τiM>0(i=u,q,r)表示相应输入的饱和值.
假设1式(2)中,所有的AUV模型参数均为未知常数且未知作用项τwi(i=u,v,w,q,r)连续有界.
假设2在纵倾复原力矩作用下,存在正常数θM,使得AUV的俯仰角满足|θ|≤θM.
假设3AUV的横向和垂向速度v和w是被动有界的,即存在正常数U0使得|v|≤U0和|w|≤U0.
2.2 控制目标
本文的控制目标是,针对由式(1)-(2)描述的AUV系统,通过设计合适的控制输入(τu,τq,τr),在满足输入饱和限制式(3)下,使得AUV 的实际轨迹η=[x y z θ ψ]T能够对期望轨迹ηd=[xdydzdθdψd]T进行跟踪,并保证跟踪误差有界.不失一般性,该期望轨迹由下述方程产生:

其中(ud,vd,wd,qd,rd)表示期望速度.
假设4期望轨迹(4)满足:1)期望速度id(i=u,v,w,q,r)及其一阶导数都是有界的,且满足|vd(t)|≤|ud(t)|和|wd(t)|≤|ud(t)|,∀t≥0;2)期望俯仰角|θd|<以避免出现奇异现象.
值得注意的是,假设4中并未对期望速度是否满足持续激励条件做任何限制,因此,期望轨迹(4)可以是持续变化的时变运动轨迹,也可以是固定点.
为便于后续控制设计,定义AUV的跟踪误差如下:
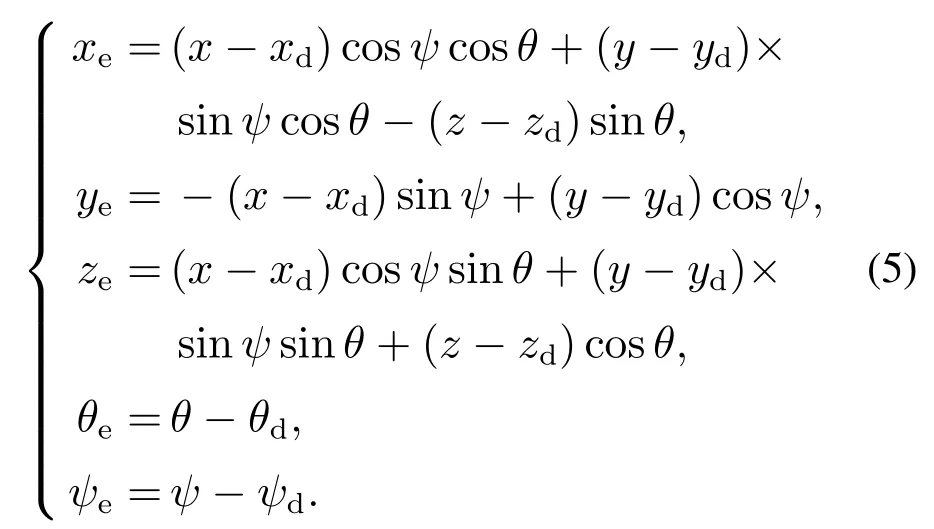
对上式求导并结合式(1)和式(4)可得

其中:ie=i-id,i=u,v,w,q,r表示速度误差;变量gx1,gx2,gy,gz1和gz2的具体表达式如下:

不难发现式(7)中各项都是有界的.此时,经过式(5)的全局可逆变换,本文所研究的控制问题等价于关于跟踪误差(xe,ye,ze,θe,ψe)的镇定问题.
3 控制器设计
为实现对式(5)中跟踪误差的镇定控制,本节将给出一种新型的饱和控制律.首先,考虑到AUV的欠驱动特性,选择误差信号ψe和θe作为虚拟控制输入分别实现对误差信号ye和ze的镇定.为此,定义以下误差修正方程:

其中δθ和δψ表示附加控制项并定义如下:

将式(8)代入式(6)可得



4 稳定性分析
下面给出本文的主要结论.
定理1针对由式(1)-(2)描述的AUV三维运动模型,当假设1-4成立时,对于如式(4)表示的期望轨迹,包括时变轨迹和固定点等,在控制器如式(13)(17)(27)作用下,结合自适应律如式(31),能够保证AUV三维跟踪误差收敛到原点附近的有界邻域内.此外,若选择控制参数ki,WiM,γi(i=u,q,r),Nh,γθ和γψ满足如下不等式:
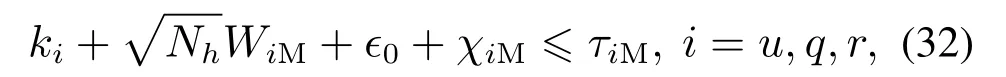

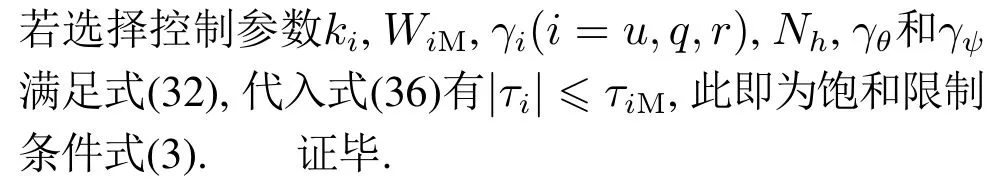
5 仿真结果
为了验证上述控制方法的有效性,本节对某型AUV的三维同步跟踪和镇定问题进行了数值仿真实验.AUV模型参数为[25]

在仿真中,期望轨迹设定为由时变轨迹和固定点构成的复合轨迹形式,其中:在仿真时间t≤150 s时,ud=1.5 m/s,其余速度和角速度均为0,即期望轨迹为 直 线;在t ∈(150,450]s 时,ud=1.5 m/s和rd=rad/s,其余速度和角速度均为0,即期望轨迹为圆形;在仿真时间t >450 s 时,期望轨迹为固定点(300 m,-100 m,-100 m,0 rad,0 rad);期望轨迹的初始状态设定为xd(0)=0 m,yd(0)=0 m,zd(0)=0 m,θd(0)=0.1 rad,ψd(0)=0 rad.AUV的初始状态为x(0)=15 m,y(0)=10 m,z(0)=-10 m,θ(0)=0 rad,ψ(0)=0 rad.AUV的初始速度和角速度均为0.控制参数选择为
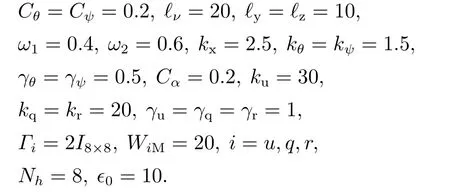
仿真结果如图1所示.为了更好地对比本文控制方法的性能,在仿真中加入了文献[8]方法的对比结果.

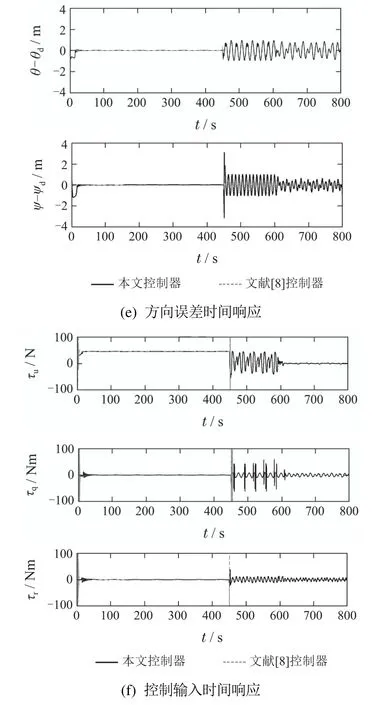
图1 欠驱动AUV三维同步跟踪和镇定仿真结果Fig.1 Simulation results for three-dimensional simultaneous tracking and stabilization of the underactuated AUV
由上述仿真结果可知,在本文控制方法作用下,AUV能够实现对复杂三维空间期望轨迹的跟踪,包括时变轨迹和固定点;跟踪误差均能收敛至零点附近的有界区域内;而对比文献[8]的控制方法只能实现时变轨迹的跟踪,当目标轨迹为固定点时,AUV的位置误差和控制输入无法收敛.且由于对比文献[8]未考虑饱和输入限制,其第一阶段时变轨迹的控制输入远大于本文的控制器;本文在饱和动力学控制式(27)作用下,所有的控制输入均始终处于饱和限制范围内,有效的避免了因控制输入过大所引起的控制失效和跟踪性能下降的问题.另外根据上图可知θ的最大值最终收敛至1左右.
6 结论
本文针对欠驱动AUV的三维同步跟踪和镇定控制问题,提出了一种基于神经网络的饱和控制方法.通过在角度跟踪误差信号中引入附加控制项,使得控制器能够在跟踪控制和镇定控制之间进行光滑切换.基于RBFNN设计了针对AUV未知参数的自适应更新律.根据Lyapunov直接法,完成了AUV控制输入的饱和化设计,保证了跟踪误差能够收敛至零点附近的有界区域内.最后对AUV三维同步跟踪和镇定问题进行了仿真实验并与已有研究进行了对比,结果表明本文控制方法无论在跟踪情况下还是镇定情况下均具有较好的控制性能,并成功避免了输入饱和现象.

