井下调度运输的自动调度策略研究
李文宏郑建志
(1.山东科技大学海洋科学与工程学院,山东青岛 266590;2.泰安华讯电气有限公司,山东泰安 271219)
1 引言
机车调度监控系统对于保障矿井机车的运输安全,提高矿井轨道机车的运输效率具有非常重要的作用,是现代化矿井必须具备的[1].随着煤矿自动化水平的提高,机车数量增多,如果没有有效的机车调度,会出现机车碰撞、井下调度效率降低问题.这就需要减少人工调度在机车调度系统中所占的比重,优化机车调度系统至完全自动调度.本文研究的目标就是提出行之有效的机车调度策略,实现机车调度监控系统可以自动调度井下机车行驶,能够避免机车碰撞,提高井下调度效率.
为了得到符合矿场结构的调度策略,首先需要对矿场路况等进行模拟,Petri网在模拟、决策和制造业中来模拟复合系统已经拥有了广泛的应用[2],机车调度过程本质上也属于离散动态系统,可以用Petri网来进行描述,有许多论文[3-4]也通过Petri网对机车调度过程进行建模研究.在本文中通过利用Petri网来模拟机车调度过程,发现其中容易发生死锁的进路或区段,通过添加约束避免死锁,进而发现实际矿场中易发生碰撞的路段并进行预防.
早在2007年郭智奇等人[2]就利用有色Petri网对机车调度系统进行了建模,但是其主要研究内容是系统本身,而没有对机车调度过程进行优化,2012年,霍晓宇等人结合矿山运输调度系统实际,考虑到计划产量、生产能力、质量要求和运输过程等方面约束,建立了一个通用性较强的矿山运输调度系统模型[5],对井下机车调度有一定的参考意义.2013年,方欢等人利用Petri网对机车调度过程进行了详细的建模并分析其无死锁调度提出了最优调度策略[4],但是未进一步将调度策略与调度系统结合解决机车调度自动化问题.2016年,V.Nguyen等人[6]分析了所谓的混合车间问题的特征,提出了一种改进的遗传算法,以最大程度地提高了混合车间计划的效率,为井下机车调度效率的提高提供了解决方案.2017年,陈晨针对铁路调度建立Petri网模型,并提出模型优化策略[7],2018年,李国清以最短工序时间间隔和最短完成时间为共同优化目标构建了地下矿山生产接续与设备调度集成优化模型[8].Renaud Sen´ecal等[9]在处理多个处理流的矿山生产调度问题中,开发并行多邻域禁忌搜索元启发式算法,以优化所提出的模型.
上述论文只是对井下调度策略进行了优化,但是还未上升到自动调度的高度,在井下自动调度方向,许多学者将方向放在机车自动化上,在2014年王建斌等人[10]就对矿井机车无人驾驶系统进行了形式化的设计与开发,李宏刚等人[11]提出了一种矿用运输车辆无人驾驶感知及控制方法,实现无人驾驶矿用运输车辆纵向速度和横向位置的精准控制.井下机车的无人控制只是井下机车自动调度系统的一部分,还需要自动调度策略,只有两者结合才能实现井下运输调度的完全自动化.
本文首先利用Petri网对井下调度过程进行了无死锁建模,然后根据矿井轨道的结构提出了3种不同参数下的最优调度策略,然后利用最优调度策略进行矿井调度参数的设置,最后通过仿真实验验证了调度策略的有效性.
2 井下Petri网建模过程
2.1 Petri网建模基本概念
时延Petri 网[12]是一个六元组N=(P,T,F,W,M,D),P代表库所Place,T代表变迁Transition,F代表有向弧.Petri网用标识M来表示系统的当前状态,用不同颜色的令牌(Token)的流动表示系统的变化状态和活动行为.
P={P1,P2,···,Pn}:Petri网中“”,即库所.
T={T1,T2,···,Tm}:Petri网中“”表示瞬时变迁,“ ”表示时延变迁.
M:Petri网中库所中的点称为令牌或者Token,其图形为“”,不同颜色的令牌定义为机车或者命令.
F:Petri网中“”,即有向弧,定义为机车和命令的流动方向.
W:代表有向弧上的权值函数,矿山机车模型中W表示一条路段同时通过的机车数量.
D:为所有库所的时延集,定义为机车通过该路段所需时间.
2.2 进路和区段的划分
图1中蓝色线段表示机车轨道,轨道附近的各种图标是机车调度监控系统的组成部分,轨道上的数字是划分的区段,区段和进路是机车调度规则中基本的元素[13],井下轨道区段和进路的划分直接影响到调度策略的形成.
图1中区段和进路的划分如表1所示,其对应的区段长度表如图2所示.
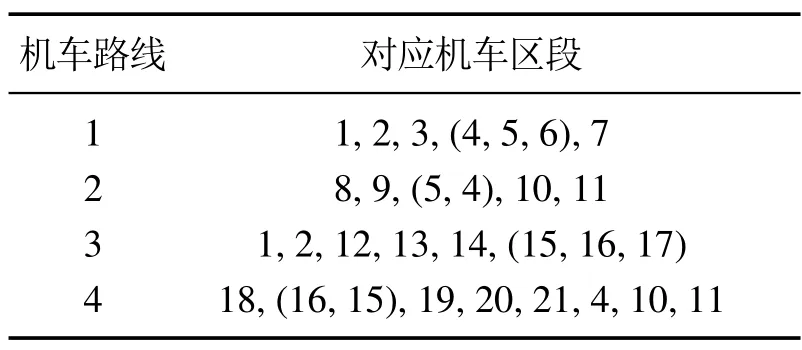
表1 路线及区段对应表Table 1 Route and section correspondence table
2.3 井下调度Petri网建模
在该节对图1矿场进行Petri网建模,图1井下轨道为单向轨,机车从图1平峒口01#车场出发,去往301盘区02#车场和303盘区03#车场,机车行驶路线1为01#车场到02#车场再返回01#车场,为变迁触发序列A,机车行驶路线2为01#车场到03#车场再返回01#车场,为变迁序列B.

图1 某煤矿界面图Fig.1 Interface diagram of a coal mine
变迁触发序列A的Petri网建模如下图2所示.
其中Pn代表n号区段,其中后缀有a和b的代表该区段为公共区段,a,b表示不同方向.黑色令牌代表空载机车,蓝色代表重载机车,黑色变迁没有时延,变迁时延Tn是机车驶过n号区段的时间.绿色的令牌代表限制库所,用来限制进路内只有一辆机车和变迁序列A调度的无死锁,可以看成机车调度监控系统中的调度命令.
整个调度流程为图2中黑色Token通过CH1车场出发,经过进路1,2,3后,经过限制库所X1,X2确定公共路段4,5可以进入后机车进入,经过进路6,7到达采矿车场02,装车后变为蓝色Token,然后返回CH1车场,再次经过路段4,5时,再次确定,之后经过10,11 到达CH1卸车再次变为黑色Token.
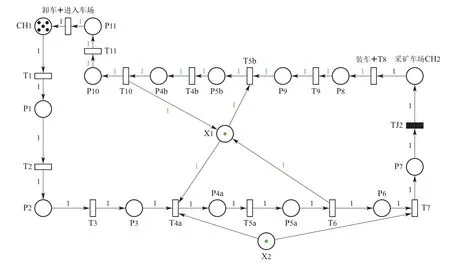
图2 变迁触发序列A的建模Fig.2 Modeling of transition trigger sequence A
变迁触发序列B的Petri网建模如下图3所示.

图3 变迁触发序列B的建模Fig.3 Modeling of transition trigger sequence B
两个变迁序列完成后,可以研究自身循环中可能出现的冲突和竞争,避免死锁的出现,但是两个变迁序列是具有交集的,所以还需要将两个变迁触发序列结合得到如图4所示的完整的井下调度建模.
3 消除死锁和冲突的分析
死锁出现的条件结合Petri网为
1) 互斥:共享令牌同一时刻只能被一个变迁序列占用.
2) 请求与保持:库所因变迁发生条件不满足时,不释放库所内令牌.
3) 不可抢占:库所内令牌不能凭空消失.
4) 循环等待:进路之间形成一种头尾相接的循环等待资源关系.
在上述4个条件中,前3个是Petri网本身的性质,是无法避免的,所以要做到模型无死锁[14]就要使条件4不满足.井下轨道公共路段使得机车进入和驶出时头尾相接,这是死锁条件4循环等待的出现原因.
冲突在Petri网中是两个变迁对一个令牌的夺取,在单轨道Petri网模型中不会出现,即在图2和图3中不会出现,只会出现在图4中T12和T3对P2中令牌的抢夺,即机车对采矿车场的选择,而机车出车时就已经确定采矿车场,所以无需对此进行设置.
3.1 模型死锁约束
变迁触发序列A中进路(4,5)是机车来回的公共路段,故4,5,6,7,8,9,CH2形成闭环回路,易形成死锁.
同理,在变迁触发序列B中,进路(15,16)是机车来回的公共路段,故15,16,17,18,CH3形成闭环回路,易形成死锁.
当上述任意库所都有令牌时,就会陷入死锁,所以防止死锁的方法是将进入区段和驶出区段错开,使死锁条件4不满足.
序列A中区段4和5是公共路段无法设置,所以将进入区段6或是驶出区段9与区段4,5形成一个新进路,只允许进入或驶出时只有1辆机车,即可避免死锁的发生,在图2中利用X2限制库所使(4,5,6)为一个进路.
同理得在变迁序列B中将(15,16,17)作为一个进路,也避免了死锁条件4的发生.
两者结合形成图4完整建模后,没有形成新的头尾相接的循环等待关系,没有形成新的死锁,但是两者都具有区段4,因此通过X1对区段4进行了约束.

图4 完整矿井下机车轨道模型Petri网建模图Fig.4 Petri net modeling diagram of complete locomotive track model in underground mine
4 调度策略的建立
井下机车在获取矿产资源的过程中,由于路线复杂,空间有限,多辆机车同时运行会发生碰撞等问题需要进行机车调度,机车调度本身是对进路和区段的分配与控制,在本节中是通过协调机车运行顺序或路段资源的分配,在保证安全的前提下,达到系统生产最优化的目的.
4.1 井下调度参数设置
通过上述证明了模型的无死锁性,但是如果不采用符合矿场的调度策略的话,会使得机车在无死锁调度的过程中浪费大量的时间.
为了方便得到井下调度策略,将井下车辆速度设为匀速v.机车数目设置为n.
机车同一序列发车时间间隔设为Td.不同序列机车发车间隔设为Tl.
机车在整个循环过程中还需要装车和卸车,卸车在01#车场不占用循环时间,装车时间分别在02#和03#车场占用循环时间,装车时间设为Tz.根据机车调度规则[2],一段进路中只能有一辆机车,由于该调度规则的原因,两辆机车之间的间隔时间等于机车占用一个库所的最长时间T.
证假设有Li(i=1,2,···,n)个区段,其中当i=m时,区段最长,库所占用时间最长.第1辆机车在轨道行驶时间为
设第2辆机车在第1辆机车驶出L1后,立刻驶出,此时间隔时间为L1/v,当到达L2之前,若L1>L2,则机车不需要等待,可以直接进入L2,此时间隔时间依然为L1/v,当L1<L2时,第1辆机车还未驶出L2,需要等待时间为(L2-L1)/v后才可进入L2,此时间隔时间为L1/v+(L2-L1)/v=L2/v.
以此类推,两辆机车间隔时间为Lm/v,为机车占用一个库所的最大时间.
所以一条变迁序列中两车之间最长的间隔时间Td可能为Lm/v或者Tz(Tz≥Lm/v).
当存在多条变迁序列时,不同变迁序列之间的间隔时间应为最长公共路段的行驶时间. 证毕.
4.2 3种情况下的调度策略
变迁触发序列A:1,2,3,4,5,6,7,8,9,5,4,10,11.
变迁触发序列B:1,2,12,13,14,15,16,17,18,16,15,19,20,21,4,10,11.
变迁触发序列A的总时间TA为

变迁触发序列B的总时间TB为
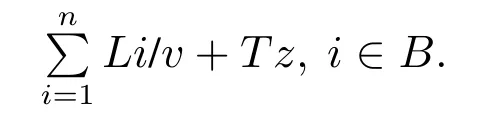
在该例中TA=7250/v+Tz,TB=9790/v+Tz,TB-TA=2540/v,且两个变迁触发序列有最长公共区段1.A,B单独发生时,变迁间隔时间为L1/v或者Tz(Tz≥L1/v).
同时发生时,A,B变迁间隔时间为L1/v,A,B单独变迁序列为2L1/v或Tz(Tz≥2L1/v).
不同的机车发车间隔时间对调度策略的优化方式是不同的,所以提出3种不同的情况:
情况1当Tz≤L1/v时,序列变迁间隔Td为L1/v,L1为序列A,B公共起始段,又因为TB >TA,所以最优调度方式即为仅触发序列A变迁.
如果井下调度要求两条变迁序列A,B都需要触发时,TB-TA=2540/v,其值与2L1/v最接近,因此触发序列设置为BAABAA···且最后触发序列必须是A时与仅触发序列A变迁时时间相同.当井下有10辆机车时变迁触发情况如图5-6所示.

图5 仅触发变迁序列AFig.5 Only trigger transition sequence A
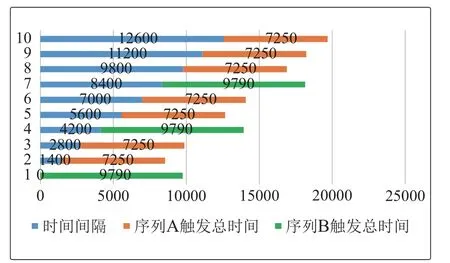
图6 序列A,B触发Fig.6 Sequence A,B trigger
从图5-6可以看出两者消耗时间一样,所以情况1下的最优调度策略为A单独触发或是BAABAA···.
情况2当L1/v≤Tz≤2L1/v时,单独触发序列A变迁时,同一序列变迁间隔Td=Tz,单独触发序列A的时间为(n-1)Tz+TA.
当序列A,B交错发生时,A,B序列之间变迁间隔Tl为L1/v,同一序列变迁间隔Td=2L1/v.
当机车数目为偶数时,最优调度方式为BABA···,当机车数目为奇数时,ABABA和BABAA的方式还需要再考虑,具体序列发生总时间公式如下:

随着机车数目n的增加,单独触发序列A的调度方式总时间越来越长,不适合多机车调度井下矿场.
情况3当Tz≥2L1/v时,同一序列变迁间隔Td=Tz,A,B序列之间变迁间隔Tl不再只是L1/v,此时最优调度策略是在序列A之间插入序列B,两者间隔时间前段为L1/v,而后段为Tz-L1/v.
由上述3种情况可以看出,当机车匀速行驶在轨道上时,机车运行速度v和装车时间Tz决定了机车行驶的最优调度策略.
4.3 轨道内部调度时间
上述最优调度策略忽略了机车在井下轨道内部经过调度系统调度的时间,是理论上的最优调度.
情况1和情况3不易发生且调度逻辑简单,机车调度时间被Tz或Tl覆盖,不再赘述.
情况2为井下调度的多数情况,因此对情况2下发生的机车调度做研究,需要机车调度的情景为变迁序列A从CH2回来的车和变迁序列A去往CH2车相遇,变迁序列A去往CH2的车和变迁序列B从CH3回来的车相遇,变迁序列B从CH3回来的车和变迁序列B去往CH3的相遇,以及变迁序列A回来的车和B回来的车竞争.
A回A去:
冲突路段为进路(4,5),当n为奇数Tz≥TBTA时机车进入(4,5)的时间区段为

解得
当n为偶数或n为奇数Tz≤TB-TA时死锁的时间区段为
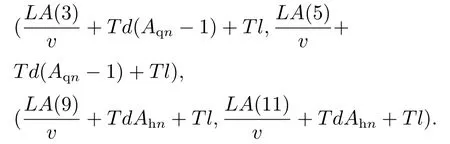
同理解得式(1).
其中:Td为机车发车间隔时间,v为机车行驶速度,Aqn为序列A去往采区车场CH2的第n辆车,序列为序列A回到车场CH1的第n辆车.LA(n)为序列A前n个进路的长度.
A去B回:
冲突路段为进路4,同理解得当n为奇数Tz≥TB-TA时机车进入进路4的死锁时间区段为
n为偶数或n为奇数Tz≤TB-TA时机车进入进路4的死锁时间区段为
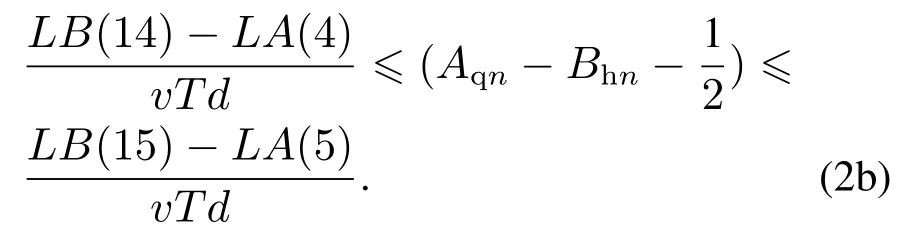
B回B去:
冲突路段为进路(15,16),同理解得当n为任意情况时机车进入进路4的死锁时间区段为
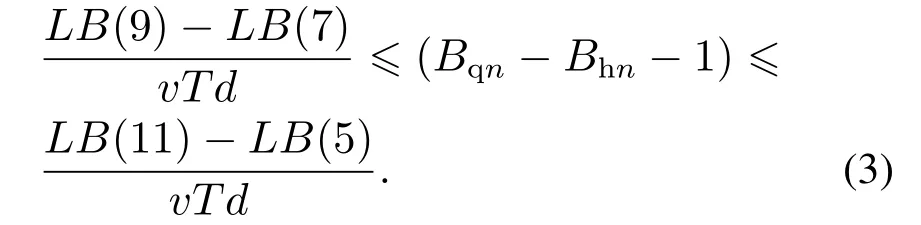
A回B回:
竞争路段为进路4,同理解得当n为奇数Tz≥TB-TA时机车进入进路4的竞争时间区段为
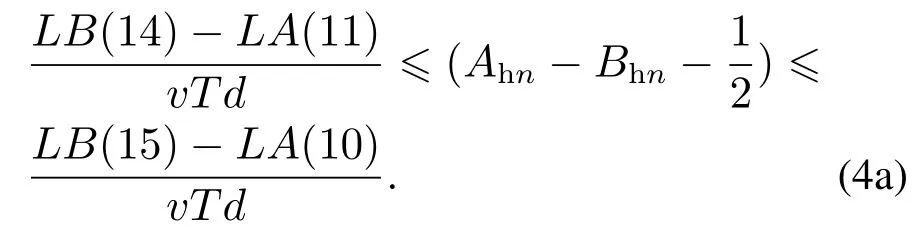
n为偶数或n为奇数时机车进入进路4的竞争时间区段为
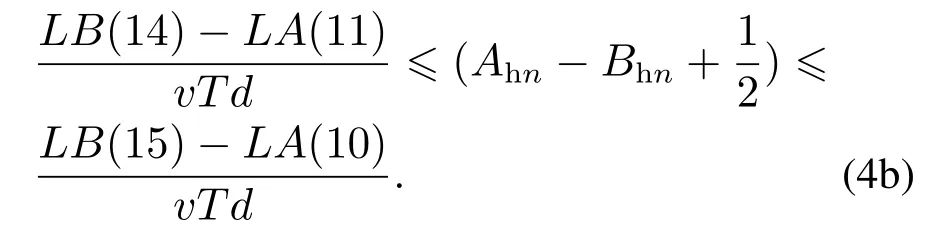
将Td=2L1/v和表2 中长度数据代入式(1)(2a)(2b)(3)(4a)(4b)得到下式:

表2 煤矿区段长度表Table 2 Coal mine section length table

其中Aqn,Ahn,Bqn,Bhn都为整数,经过计算发现上述条件都不满足.
从上述过程可以发现,当机车发车间隔Td与机车速度v相关时,机车死锁和竞争的发生与两者都没有关系,只与机车区段长度有关,而机车发车间隔Td的设置针对不同的情况有不同的值,上述策略确定后结合Petri网模型可以通过可达树[15]进行时间上的优化.
5 实验过程
本文的自动调度策略是对山西王坪矿场结构研究得到的,是为在该矿场井下安装KJ654调度监控系统做准备,在整个机车调度系统研发完成后,首先通过人工模拟井下机车运行对调度监控系统的信号灯、位置传感器等设备进行有效性进行验证,人工模拟时数据如下:

从数据中可以看出,在人工模拟机车过程中,机车车场等待时间为5 min,E3号车从01车场到02车场时间为22 min左右.E4号车从01车场到03车场时间为28 min左右.
机车在井下并非匀速行驶,但结合表2可以看出L1/v≤Tz≤2L1/v且Tz≤TB-TA,实际调度共有19辆机车,选择情况2下BABA...A作为调度顺序.
选择好调度策略后,由于人工难以完全模拟距离与速度的变化,该实验为仿真实验,将速度设置为Tz=2L1/v,Tz不变为5 min,得v=m/s,算出每个变迁T的时间,将Petri网模型中每个变迁的时延设定好之后,设定机车数目为9辆,通过图4 Petri网模型进行仿真实验,调度数据对比如表3所示,1为数据库数据,2为实验数据.

表3 调度数据对比表Table 3 Dispatching data comparison table
考虑到井下机车的速度具有一定的限制,速度不变进行实验仿真,对比如表4所示.
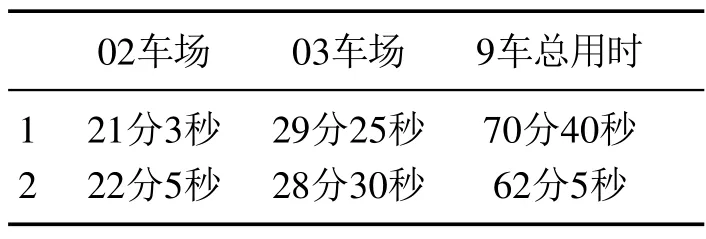
表4 调度数据对比表Table 4 Dispatching data comparison table
在速度大约一致时,虽然单一车场时间相似,但多辆机车时使用调度策略的也要更快一点.
在实际应用过程中,该矿场井下有运料车,运人车及运煤车各类车辆30余辆,速度不一致,情况较复杂,但运煤车为普通矿车,速度约为3~4 m/s,矿车车皮数非常多,所以机车装卸车时间比较长,所以选择情况3下的调度策略.
在井下安装设备测试时出现了不少问题,硬件问题居多,而在调度策略方面,是因为机车损坏等井下突发情况的出现,所以最后的机车调度监控系统还是保留了人工调度的功能,并未完全依赖自动调度,但是依然能证明该调度策略能够指导井下机车调度,提高调度效率.
6 结论
本文使用Petri网结合井下调度监控系统结构,以真实井下矿场为实例,提出了机车在井下轨道行驶下的Petri网模型,基于该无死锁模型建立了模拟专业调度人员控制机车运行的调度策略.并对调度策略进行了理论验证,最后通过仿真实验以及实际应用验证了调度策略的有效性.为井下自动调度系统的形成提供了行之有效的自动调度策略.

