不对称欠驱动水面机器人事件触发全局渐近镇定控制

王 锐 ,司昌龙 ,马 慧 ,郝程鹏

(1.中国科学院声学研究所中科院水下航行器信息技术重点实验室,北京 100190;2.中国科学院大学,北京 100049)

1 引言

欠驱动水面机器人(under-actuated surface vessels,USVs)已在军事领域与民用领域得到了广泛的应用,可以完成海上巡逻、自主航行、打捞、搜救等任务.由于不存在侧向控制力,使USV成为具有二阶非完整约束的欠驱动系统,导致USV的控制问题具有一定的挑战性并得到了广泛关注[1-2].根据不同任务需求,USV的控制目标主要可以分为:镇定控制[2-12]、轨迹跟踪[13-14]、路径跟踪[15-17].

其中,镇定控制可以使USV完成动力定位以及自主停靠等任务,控制目标为设计控制器使USV所有状态均收敛至给定的参考点.其难点在于USV系统原点不满足Brockett条件[18],即时不变光滑的状态反馈控制律无法使系统渐近稳定.因此需要设计光滑时变[2-6]或不连续[7-12]的控制律.文献[3]首次利用坐标变换以及级联系统理论将USV的镇定控制问题简化为4阶子系统的镇定控制问题,并引入关于时间t的三角函数设计光滑时变控制律使USV原点渐近收敛.在文献[3]的基础上,国内外学者们进行了一系列的改进[4-11].文献[4]提出了若干光滑时变控制律,首次实现了USV原点的指数收敛.文献[5]利用频率实化的变周期函数代替周期三角函数设计了光滑时变控制律,提高了系统的收敛速率;文献[7]利用反步法设计了非光滑的控制律,并利用切换控制律避免系统奇异现象;文献[8]提出的切换控制律首次实现了系统原点的κ指数收敛.为了增加系统的鲁棒性,文献[9-10]提出了简单的比例微分(PD)控制器,由于牺牲了终端姿态角的自由度来增加系统鲁棒性,无法实现最终航向角的镇定,仅实现了USV的位置镇定,并利用中心流形定理以及LaSalle定理证明了位置坐标的渐近稳定性.以上文献中均假设USV 是上下对称的,并不符合实际应用[14],需考虑USV不对称的情况.文献[6,11]利用坐标变换证明了不对称USV的镇定控制也可以等价于类似文献[3]中子系统的镇定控制问题,并设计切换控制律使不对称USV 原点渐近稳定[11],以及设计光滑时变控制律实现不对称USV原点的κ指数收敛[6].

上述方法均是基于连续时间系统进行USV镇定控制器设计,系统内部的采样时间是固定的,即当系统到达下一个采样周期时,完成对控制信号的更新.若采样频率过高,不仅过度占用系统的资源,而且执行器执行次数过多,会减少执行机构使用寿命[15,19],而对控制品质提高的程度有限;若采样频率过低,虽然节约了系统资源,但是控制品质随之变差.为了解决上述问题,文献[13,15-17]利用事件触发机制(eventtriggering mechanism,ETM)预设触发条件,设计USV事件触发控制器(event-triggered controller,ETC)实现了USV的轨迹跟踪[13]以及路径跟踪[15-17].ETC的优点在于,系统仅在满足触发条件的时刻更新控制量,可以节约系统资源以及减少执行器操纵次数,同时维持原有的控制品质.

通过以上分析可知,关于USV的ETC研究成果很少,且多集中于轨迹跟踪以及路径跟踪问题.文献[2,20]指出,由于需要同时约束USV的位置以及航向,USV的镇定控制比轨迹跟踪和路径跟踪更难实现,因此用于轨迹跟踪以及路径跟踪的ETC对于不对称USV的镇定控制并不适用.迄今仅文献[12]利用T-S模糊规则描述对称USV的数学模型,结合ETM 提出了ETC以实现对称USV的渐近镇定控制.然而在利用模糊规则建模时限制了USV的状态变化范围,导致结果并非全局的.

综上所述,至今仍没有关于对称/不对称USV 的ETC以保证系统原点全局渐近稳定.为了解决这一问题,结合实际的工程应用,本文提出了一种ETC设计方法,以实现不对称USV 的全局渐近镇定控制.受以上文献启发,本文采用坐标变换以及级联系统理论将不对称USV的全局渐近镇定控制问题等价于欠驱动子系统的全局渐近镇定控制问题,通过引入时变函数构造辅助变量以设计控制推力以及理想航向角速度,进而设计控制力矩使不对称USV跟踪理想角速度,并结合基于切换策略的ETM得到关于控制推力以及控制力矩的ETC输入,使不对称USV闭环系统原点全局渐近稳定(globally asymptotically stable,GAS),最后通过仿真验证所设计ETC的有效性.

2 模型变换

不对称USV的运动学动力学模型为[1,13]

利用式(2),可将系统(1)改写为

对于系统(5),利用文献[10]中的如下结论:

引理1状态变换(4)是全局微分同胚的,系统(1)的镇定问题可以转化为系统(5)的镇定问题.

引理2如果存在控制律使子系统(5b)的状态全局有界且GAS,则该控制律能使系统(5)的状态全局有界且GAS.

利用以上两个引理,可将不对称USV全局渐近镇定控制任务转化为:设计关于控制推力τ1以及控制力矩τ2的ETC,使子系统(5b)的原点GAS.

3 主要结论

为了便于设计与分析,给出如下定义与引理:

3.1 ETC设计

定义采样误差Δi=ϖi(t)-τi(t),其中ϖi(t)为ETC控制信号.受文献[22]的启发,设计事件触发条件为

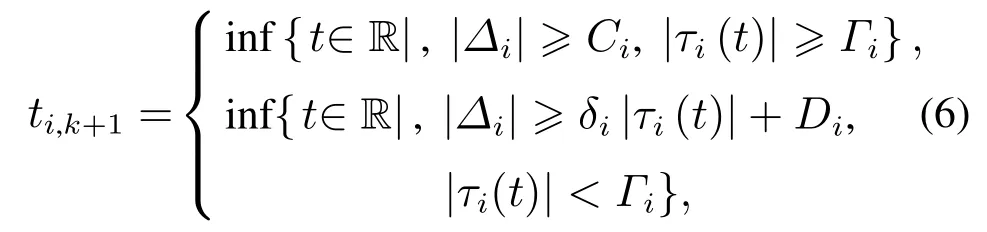
其中:k ∈Z表示记录控制器触发时刻的下标,ti,0=0为初始时刻;ETM设计参数满足:Ci,Di,Γi ＞0;0＜δi ＜1.

观察式(5b)可知,系统为欠驱动系统,为了设计时变控制律以满足Brockett条件解决欠驱动问题,利用时间周期函数ht构造第1个辅助变量ξ1=z4+Φ(z2)ht.首先利用ξ1设计控制力τ1与理想角速度z6d渐近镇定系统(5b)的前3个方程,再设计τ2使z6渐近跟踪z6d,保证闭环系统GAS.控制系统框图及ETC结构图如图1-2所示.

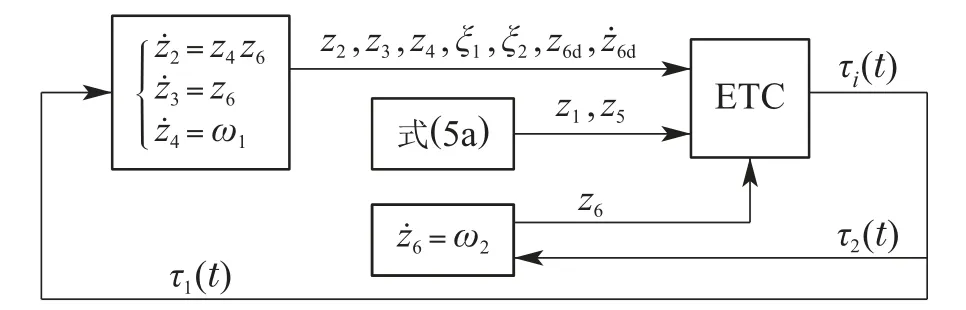
图1 控制系统框图Fig.1 Diagram of the control system

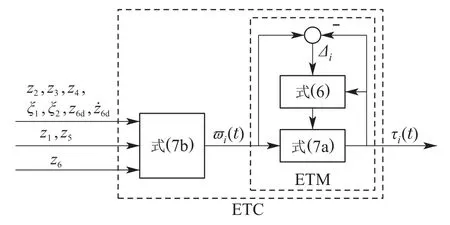
图2 ETC结构图Fig.2 Structure of the ETC

注1上述过程可以概括为ETC在触发时刻ti,k对信号ϖi(t)进行采样,并在t ∈[ti,k,ti,k+1)内保持为τi(t)=ϖi(ti,k),当采样误差Δi再次满足触发条件(6)时,记录该触发时刻为ti,k+1并再次对ϖi(t)进行采样,ETC控制量更新为ϖi(ti,k+1)并保持至下一触发时刻.

注2上述方法的优点在于预设切换门限Γi,当|τi(t)|≥Γi时,控制幅值较大,此时ETC按固定门限策略|Δi|≥Ci触发,可以避免控制信号产生突变,防止系统震荡;当|τi(t)|＜Γi时,控制幅值较小,此时ETC按比例门限策略|Δi|≥δi|τi(t)|+Di触发,可以实现精确控制,保证系统控制精度.此外,,控制量大小恒为,从而该时间段内ETC无需与外界通信,而且也减少了执行机构的操纵次数,节约系统资源.

注3当ξ1与～r的幅值较大时,式(7b)中ϖi(t)第1,3项起主要控制作用,可使|ξ1|与||快速减小;当|ξ1|与||接近于0时,ϖi(t)第1,2项起主要控制作用,可以补偿采样误差Δi对系统的影响,提高控制精度.

注4文献[3]中已证明,利用坐标变换,对称USV的全局渐近镇定控制问题也可以转化为全局渐近镇定子系统(5b),因此本文所提出的ETC设计思路也适用于对称USV的全局渐近镇定控制任务.

3.2 稳定性分析

本文的主要结果由如下两个定理给出:

4 仿真验证

为了验证所提方法的有效性,本文与文献[4]中的方法进行了对比,采样周期设为0.05 s.仿真结果如图3-12所示.

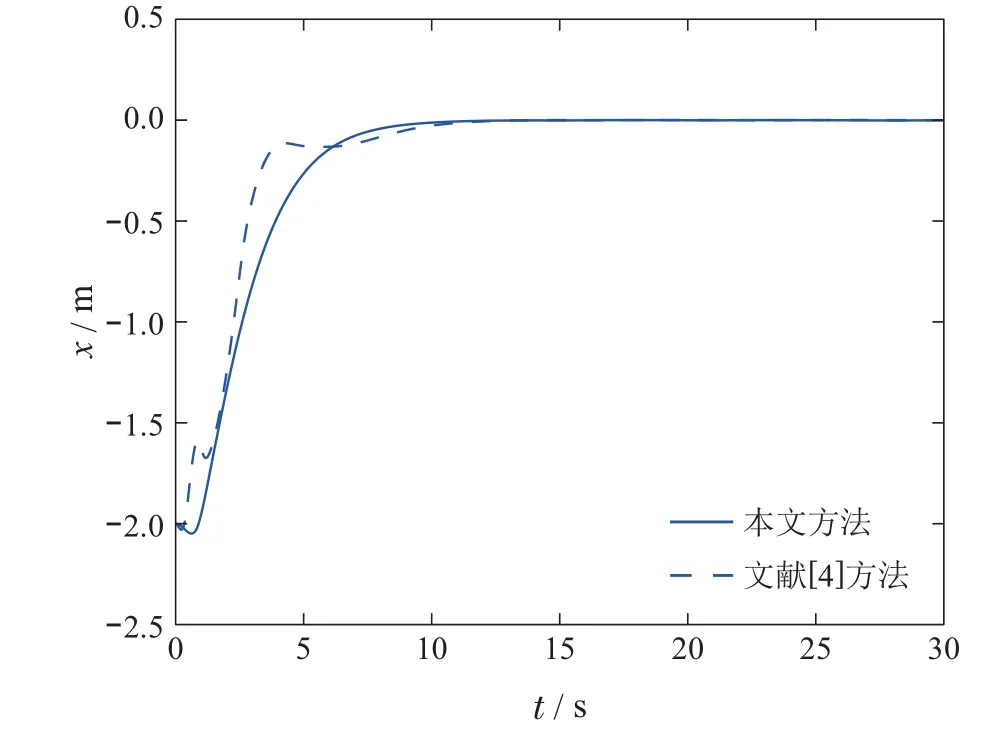
图3 x轴位置坐标Fig.3 x-coordinate position

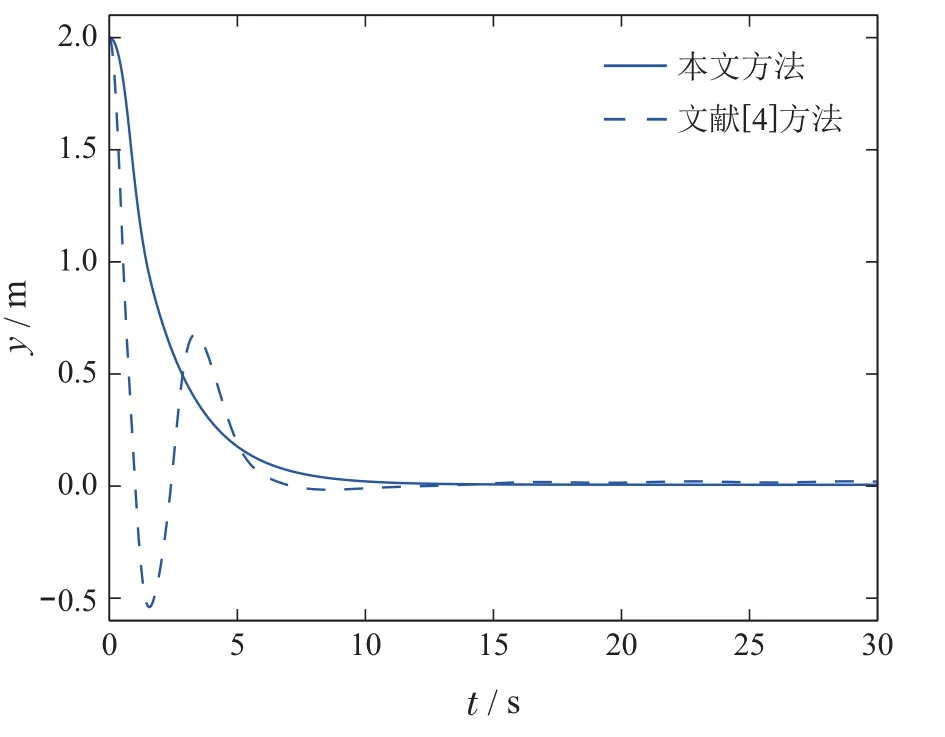
图4 y轴位置坐标Fig.4 y-coordinate position

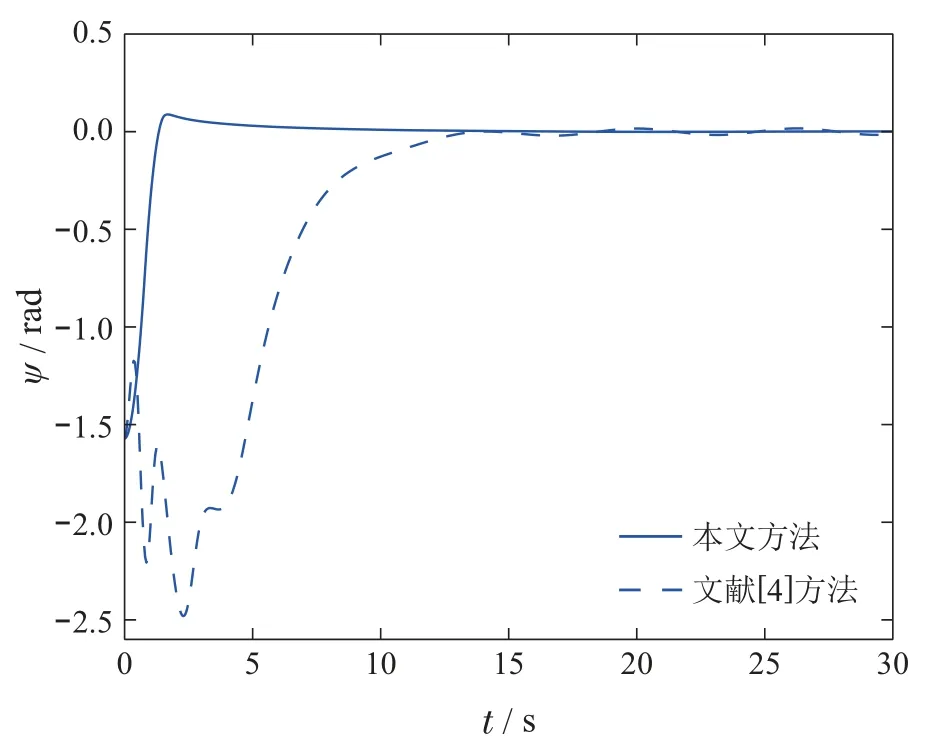
图5 航向角ψFig.5 Yaw angle ψ

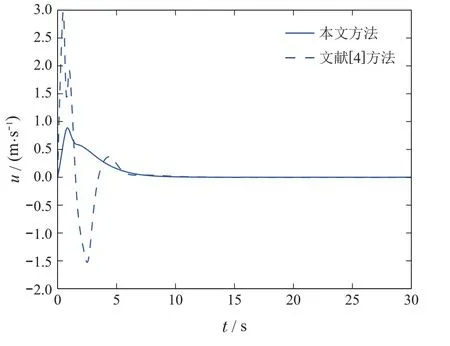
图6 纵向速度uFig.6 Surge velocity u

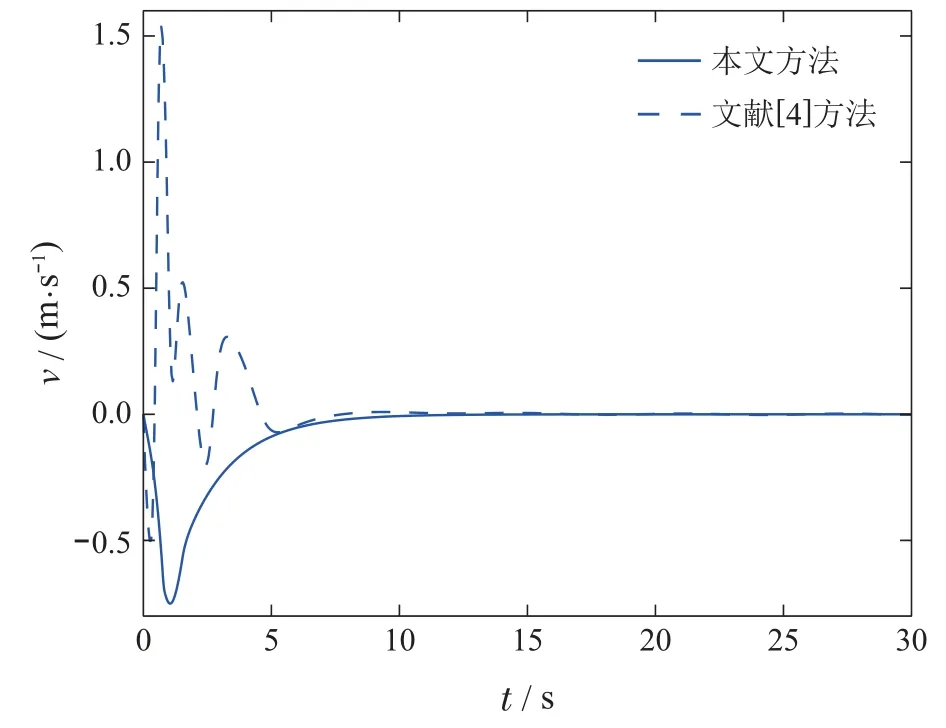
图7 横向速度vFig.7 Sway velocity v

图3-8为不对称USV的状态变化曲线,结果表明,相比于文献[4]中提出的方法,本文所提出的ETC具有更小的震荡与超调.这是由于初始时刻文献[4]的控制输入幅值较大且受到零阶保持器的作用,导致了系统各个状态变化剧烈.

由图8 可知,系统最大瞬时航向角速度达到了-3 rad/s以上,对于USV系统来说是不可能实现的.由于本文引入了切换门限ETM并补偿了Δi,可以避免控制信号的剧烈变化,防止系统震荡.

图8 航向角速度rFig.8 Yaw angular velocity r

图9-10为本文控制输入的变化曲线,由图可知,τi在触发时刻对信号ϖi(t)采样并对控制输入进行更新.定义能量消耗指标变化曲线如图13所示,由图可知文献[4]的方法控制幅值较大,需消耗更多能量,而本文所提出的ETC利用更少的能量可以达到更好的控制效果.

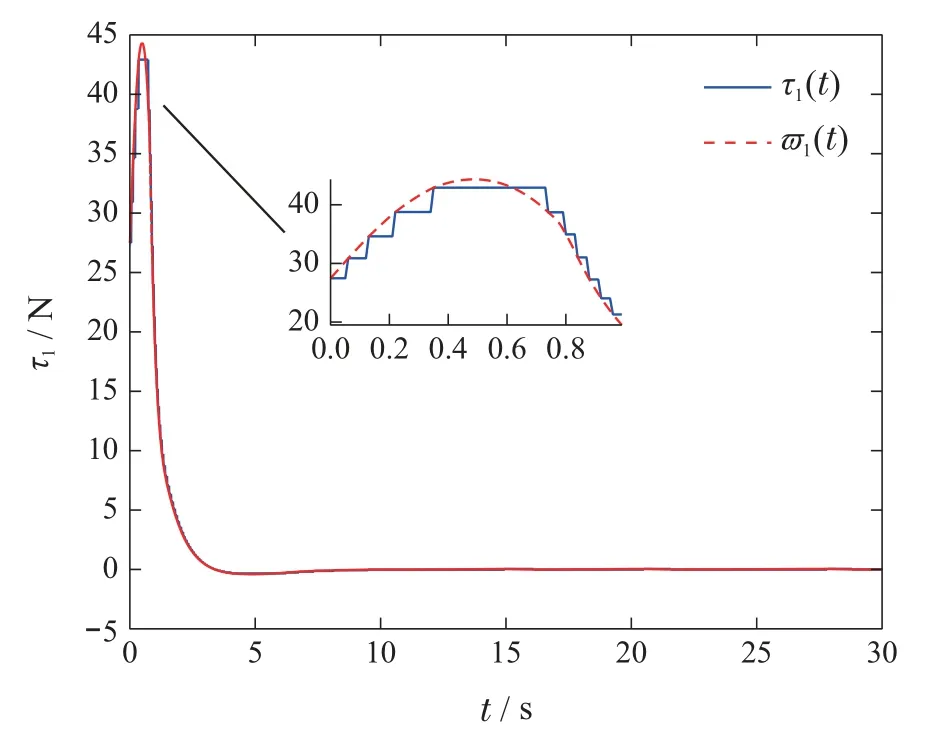
图9 控制推力τ1Fig.9 Control force τ1

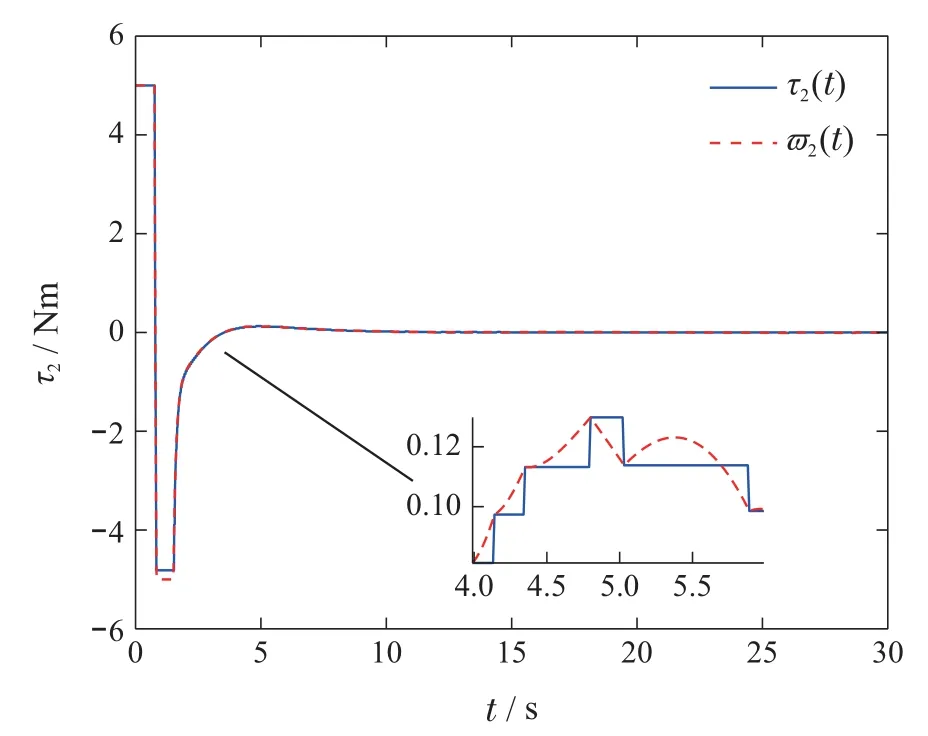
图10 控制力矩τ2Fig.10 Control moment τ2

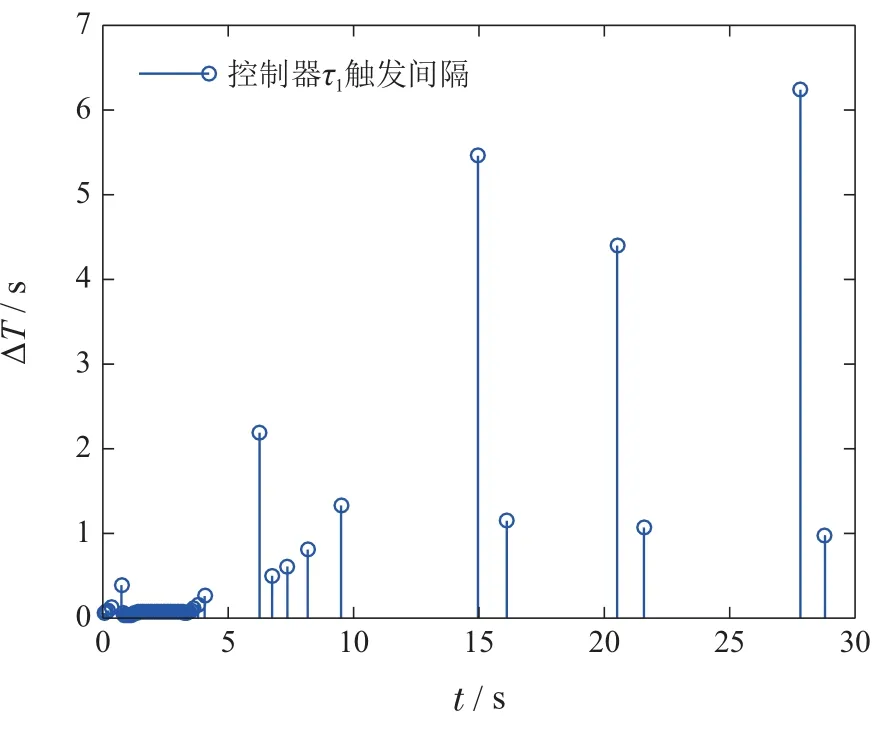
图11 τ1触发间隔Fig.11 Triggering intervals of τ1

图12 τ2触发间隔Fig.12 Triggering intervals of τ2

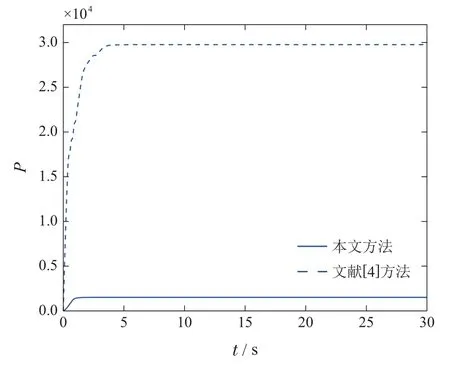
图13 控制器能量消耗Fig.13 Energy consumption of the controllers

图11-12为本文ETC中τi各触发时刻的间隔,结合图14可知,文献[4]中由于采样周期为0.05 s,控制输入在前30 s更新了600次;而采用本文设计的ETC,在前30 s控制力τ1更新了62次,控制力矩τ2更新了90次,执行机构的操纵次数显著减少,可以减轻系统的负担.

图14 控制器更新次数Fig.14 Times for update of the controllers

5 结论

本文通过坐标变换将不对称欠驱动水面机器人的全局渐近镇定控制问题转化为欠驱动子系统的全局渐近镇定控制问题,针对变换后的系统,利用周期时间函数构造时变辅助变量设计控制推力以及理想航向角速度,并设计控制力矩实现对理想航向角速度的渐近跟踪,结合切换门限事件触发机制设计事件触发全局渐近镇定控制器使闭环系统全局渐近稳定,并证明了该控制器是因果可实现的且不会发生Zeno现象.本文方法仅在系统满足触发条件时对控制器进行更新,能够节约系统资源以及减少执行器操纵次数,同时不会降低原有的控制品质.最后,仿真结果验证了所提出方法的有效性.