基于均值改进控制策略的昂贵约束并行代理优化算法

林成龙,马义中,肖甜丽

(南京理工大学经济管理学院,江苏南京 210094)

1 引言

随着计算机仿真建模软件中的有限元分析,计算流体力学等技术在航空航天、产品优化设计及可靠性工程等领域的广泛应用,高精度仿真建模方法减少实物试验成本的同时有效提升了产品质量特性[1-2].但随着市场对产品更新速度和产品质量要求的不断提高,完全依靠仿真建模技术进行设计和验证往往需要耗费大量时间成本.例如,福特汽车进行一次碰撞仿真试验需要36～120 h,那么进行100次就至少需要5个月的时间[3].尽管计算机计算能力大幅度提升,但如果碰撞试验在10种方案下进行,那么重复100次试验需要4年多的时间,这对企业而言是难以承受的昂贵时间.对于实际中的工程优化和产品设计优化,仅依靠有限试验数据近似建模难以保证代理模型预测精度.所以采用高效空间填充策略增加新增试验点,实现代理模型重构对提升模型精度及优化效率至关重要.此外,大量封装的商用仿真软件无法修改且难以获得设计变量和质量目标之间的内在关系,这种黑箱特性给优化和分析带来了极大困难[4].综上,为了减少昂贵仿真的计算次数和仿真试验成本,采用有限试验数据建立初始代理模型,选取高效的填充策略实现工程问题的并行代理优化(parallel surrogate-based optimization,PSBO)研究成为热点[1,5-6].

并行代理优化算法是基于真实试验数据或有限仿真数据建立近似代理模型,选取高效的多点填充策略对未试验区域进行选点,然后利用计算机的并行计算能力引导新试验点快速收敛到优化问题的全局最优解的办法.因此,代理模型的选择和空间探索多点填充准则是并行代理优化算法实现的关键,常用的代理模型有径向基函数方法、多项式响应曲面法、支持向量机模型及Kriging模型等[1,5-6].其中,Jones等利用Kriging模型对未试验点的不确定性度量能力,选择满足最大期望改进(expected improvement,EI)值的点作为新样本点,实现串行序贯填充的有效全局优化(efficient global optimization,EGO)算法获得了极大发展[1,5,7-8].该方法有效减少了昂贵仿真的时间成本和实物试验的物料成本,被广泛地应用于航空航天、机械工程和工业工程等诸多领域[1-2,5].

现有的代理优化算法多采用串行序贯加点策略,即在每次优化过程只选取一个新样本点进行试验或仿真,待上一次试验结束后再进行下一次试验.例如,Jones等将优化搜索和代理模型空间填充相结合,提出了最大化EI准则辅助下的标准EGO算法,但EI准则的贪婪性导致收敛速度缓慢[7];Schonlau等针对EI准则收敛缓慢问题,提出了广义参数调整的期望改进准则及包含约束处理的约束期望改进(constraint expected improvement,CEI)准则[8];Ulmer等采用最大化概率改进(probability of improvement,PoI)策略,选取Kriging 代理模型解决昂贵成本的工程优化问题[9];Alexandrov和Dennis等通过选取参数阈值,提出了模型预测值的较低置信下界(lower confidence boundary,LCB)框架并将其用于近似优化问题[10].上述策略均是基于改进增量进行优化设计的单点串行序贯填充准则,优化算法中Kriging模型的刷新和下一个样本点的选取必须等待上一次试验的结束,难以有效利用工程问题中丰富的计算资源[11-12].

随着仿真对象日益复杂,采用多台计算机或多核心计算机同时执行仿真或计算任务的并行计算有效减少了设计周期,已成为缩短产品研发时间,提高设计优化效率的常规方法.Ginbingour等的理论分析与实际验证结果表明Kriging模型在并行优化领域具有独特优势,基于Kriging代理模型开发适应于并行计算的多点填充策略逐渐成为解决计算瓶颈,提升设计效率的研究热点[12-13].现阶段基于Kriging模型多点填充策略的研究主要集中于多次优化同一加点策略进行空间填充.例如,Ginsbourger等基于严格推动提出的q-EI多点填充策略及为解决变量较多时q-EI策略计算困难问题,发展的Kriging Believer 和Constant Liar填充策略.Kriging Believer和Constant Liar策略分别选取预测均值和初始样本集最小值作为响应的伪值来近似q-EI策略,近似效果较好.但随着单次填充样本点个数q增大,并行优化效率提升不明显[13];Zhan基于影响力函数的距离特性构造了伪期望改进(pseudo expected improvement,PEI)填充策略,该策略有效提升了优化效率但未对其进行具体的理论分析与证明[14];此外,张建侠等发展了兼具局部开放和全局探索功能结合Pareto解集挑选的多目标MS&CA策略并将其应用于压力容器优化设计,但当单次新增样本数q大于3时,收敛效率提升不明显[15];此外,Viana等采用多种代理模型分别建模,利用不同模型预测能力进行试验点选取实现多点填充并将其应用于稳健优化设计[16];Hamza等提出多种策略分别选取试验点的方法进行多点填充设计并将其应用于车体碰撞优化设计[17];陈志旺等提出了融合多属性决策的双层种群筛选策略求解高斯模型参数并将其应用于多目标优化问题中[18].更多关于多点填充设计方案请参见综述性文献[12,19].

在实际工程优化中,昂贵约束并行优化问题的挑战来源于缺乏合适的多点填充策略和设计空间中可行解的获取.因此,如何进行有效的多点填充设计和可行解获取成为并行优化算法的关键.针对上述问题,文章的主要思想及框架为:首先,依据贝叶斯先验假设,后验分析及Kriging近似模型的插值特性,经过理论推导与分析给出了均值改进,未试验样本点及新增样本点三者之间的不等关系.其次,基于理论推导结果定义控制函数,结合Kriging模型最大改进特性构造具有空间调整距离特性的均值改进控制(mean improvement control,MIC)策略及拓展的期望改进控制(expected improvement control,EIC)策略实现多点样本填充设计,选取经典的可行性概率(probability of feasibility,PoF)策略作为MIC或EIC策略权重兼顾可行解的可行区域探索.然后,针对具有黑箱特性昂贵约束优化问题,综合启发式搜索算法中的差分进化优化算法,Kriging模型及约束均值改进控制(constraint mean improvement control,CMIC)填充策略和基于最大改进期望拓展的约束期望改进控制(constraint expected improvement control,CEIC)多点填充策略,提出了适用于多核计算机或多台计算机并行计算环境,基于约束均值改进控制策略的并行代理优化算法.最后,选取经典测试函数及航空减速器优化设计案例进行验证分析.文章的主要创新点及贡献:1)给出改进控制函数(control function,CF)的定义及其理论证明;2)提出了基于均值改进控制的CMIC多点填充策略及拓展的CEIC多点填充策略;3)对于Zhan等人提出的PEI策略给出了理论分析与解释[14].

2 Kriging模型

假定试验数据为n次试验获取结果,记初始观测矩阵为X=[x1x2··· xn]T,x ∈Rd及对应的响应矩阵y=[y1y2··· yn]Ty ∈R,初始样本集记为Ω=[X,y].Kriging模型将黑箱函数y(x)看作包含回归项的随机过程Y(x)的一次实现.即任意设计点x对应的响应值Y(x)表示随机过程的可能取值之一:

其中:μ为全局趋势项,反映近似目标函数在设计空间的总体分布趋势;z(x)是均值为零、方差为的平稳高斯过程,表示对近似模型的校正.

z(x)对Kriging模型的近似能力起决定性作用,其空间分布数据的协方差满足如下关系:

其中:R(xi,xj|θ)为Kriging核函数;θ为核函数的关键参数,具备自适应调节设计点之间相关性能力.本文选取满足如下关系的高斯核函数:

基于上述信息,Kriging近似模型可由式(1)改写为如下形式:

3 基于改进控制的均值改进控制策略

3.1 最大均值改进策略

样本集Ω中已知响应的最小值记为ymin,设计空间中Kriging模型可获得未知试验点的预测响应值Y(x),则ymin相较于Y(x)的最大改进表示如下:

Kriging模型在未知试验点的响应值Y(x)的最大预测改进的均值MI(x)=M[I(x)]=ymin-整理可得均值改进(mean improvement,MI)策略如下:

3.2 最大期望改进策略

其中Φ(·)和φ(·)分别表示标准正态分布累计概率密度函数和概率密度函数.

3.3 均值改进控制函数

3.4 均值改进控制策略

由定理1可得,I(x)的改进范围受到预测均值ˆy与控制函数CF的双重作用.由定理1不等式关系知:控制函数主要依据选择填充策略增加的样本点xm与未试验点x间的距离关系对改进增量进行约束控制且取值满足0 ≤CF(x)≤1;因此,将CF(x)作为I(x)的权重得到IC(x)=I(x)·CF(x).易知IC(x)≤I(x),故可以实现对I(x)改进的逐步减少.综上,基于控制函数构建均值改进控制策略:

由式(10)及第3.3节解控制函数的定义可知:在初始Kriging模型超参数一定时,当未试验点x与xm越近,控制函数越接近于1,倾向于在xm附近进行加点,ymin-的值减小幅度较小,注重局部搜索能力;当未试验点x与xm越远,控制函数越接近于0,倾向于远离xm处进行加点,ymin-的值减小幅度较大,注重全局探索能力.

同理,可得基于均值改进控制的期望控制策略:

Zhan等提出的PEI策略认为Kriging模型某一点x目标值受附近点影响较大,但距离较远的点对x影响较小.PEI策略有效减少了昂贵仿真成本,但未给出理论证明[14].MIC策略与EIC策略的理论分析表明,采用控制函数CF(CF∈[0,1])作用于最大改进I(x)来逐步减少MI或EI填充策略的贪婪特性.对于PEI填充策略而言,作用机理与EIC策略等价.因此,本文的理论分析结果可用于PEI策略的解释分析.

假设单次循环过程MIC和EIC填充一次增加q个点,可得两种均值改进控制策略表达式:

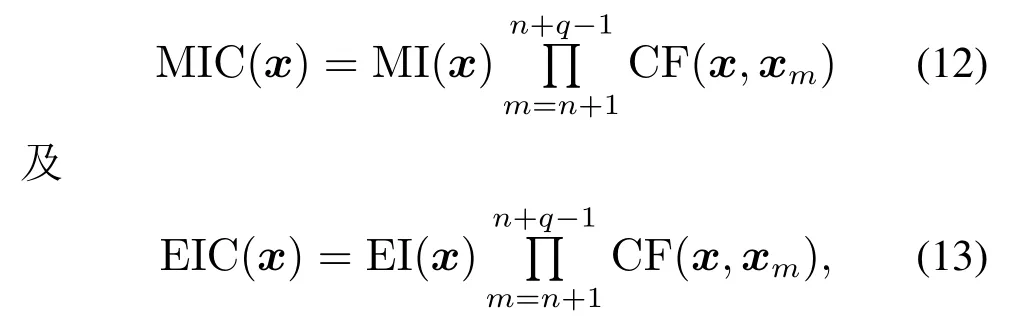
其中:xn+1为最大化MI或EI策略获取的第1个新增试验点;xn+q-1为第q个新增试验点.易知CF∈[0,1],故EIC ≤EI,MIC ≤MI,依据Bull关于EGO算法收敛率问题的证明及分析,可知均值改进控制策略具有较好的收敛性,具体理论分析结果参见文献[20].

4 基于均值改进控制策略的并行代理优化算法

4.1 可行性概率

实际工程中,基于专家经验及结构限制等因素,优化问题往往存在众多的约束条件.假设昂贵约束优化问题存在r个约束条件gi(x)≤0(i=1,2,···,r),各约束条件间彼此相互独立,空间内任意点x对应的约束响应gi(x)是满足正态分布gi(x)～N的随机变量,令G=表示约束Kriging模型的联合后验分布,则试验点x落入可行域的可行性概率可表示为如下形式:

其中P(G(x)≤0)表示满足所有r个约束条件的约束概率.

4.2 约束均值改进控制策略

Schonlau等假设优化目标函数与约束条件函数的随机过程相互独立,提出了适应于单目标约束优化问题的约束期望改进CEI填充策略[8].在Schonlau等假设条件下,将满足约束的概率和目标函数的改善概率结合,得到兼顾当前最佳设计点改进和满足约束的概率P[I(x)∩G(x)]=P[I(x)]·P[G(x)];计算均值改进和约束同时满足条件下I(x)∩Gi(x)的期望,得到CEI(x)=E[I(x)∩Gi(x)]=EI(x)·PoF(x).因此,将PoF 作为MIC多点填充策略的权重,得到两种约束均值改进控制策略

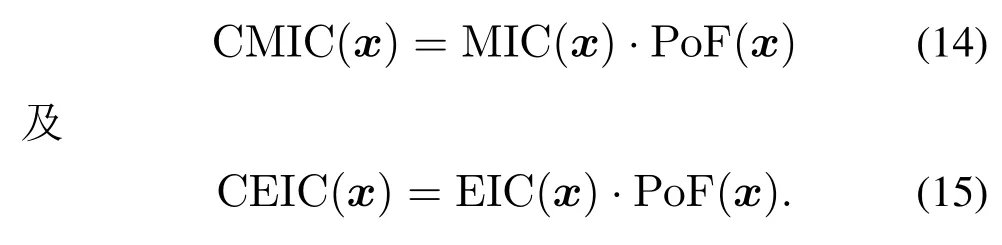
4.3 算法复杂度分析

实际优化问题中,大多数问题数据集均呈现离散化特性,因此有必要进行算法复杂度分析.代理优化算法是典型的两阶段优化过程:基于试验设计的代理模型建立(刷新)和基于空间填充设计的新试验点获取.因此,CMIC-PSBO及CEIC-PSBO算法复杂度主要来源于两部分:第1部分是代理模型的建立,单目标约束优化问题最终近似优化解数目为1,故其时间复杂度为O[tq(1+r)],r和t分别是约束条件个数和算法最大循环迭代次数;第2部分则来源于CMIC策略及CEIC策略的多点填充寻优,时间复杂度为O[tq].综上,CMIC-PSBO和CEIC-PSBO算法的整体复杂度均为O[tq(1+r)].

CMIC-PSBO和CEIC-PSBO算法二者的区别主要来自于第2部分关于MI值和EI值的计算.在预测均值和预测方差已知情况下,MI只需进行1次减法运算,EI则需要进行9次运算.故相比较CMIC-PSBO算法运算效率高于CEIC-PSBO算法.

4.4 算法实现步骤

综合运用Kriging模型,均值改进控制策略及差分进化算法,基于均值改进控制的昂贵约束并行优化算法实现步骤如下:

步骤1算法初始化(试验参数设定).算法终止条件选取;仿真案例选取;初始观测样本数量5d;填充策略单次增加新试验点个数q;

步骤2初始试验设计.拉丁超立方抽取5d个初始观测样本X=[x1x2··· xn]T,n=5d,并仿真获得对应的估计值矩阵y=[y1y2··· yn]T;

步骤3判断优化结果是否迭代达到终止条件.若是,算法终止;若否,重复步骤4-5-3;

1.4.5 BALF和血清肿瘤坏死因子-α(tumor necrosis factor -α, TNF-α)浓度测定 采用ELISA法检测BALF上清液和血清中的TNF-α浓度，试剂盒购自上海森雄科技实业有限公司。

步骤4判断样本集Ω=[X,y]中是否存在可行解G(x)≤0.若否,选取PoF策略作为填充设计方案;若是,选取均值控制策略作为填充设计方案;

步骤5算法迭代.依据样本集Ω=[X,y]建立初始Kriging模型,利用差分进化算法获取满足最大化均值改进控制策略的q个新增样本点,并刷新观测矩阵X=X ∪xn+1∪xn+2∪···∪xn+q;仿真试验计算q个新增样本点所对应的响应估计值,并刷新响应矩阵y=y ∪yn+1∪yn+2∪···∪yn+q及Kriging模型;

步骤6算法终止.输出近似最优解.

5 仿真测试及结果分析

为保证所提算法的有效性,选取2个数学算例及航空减速器优化实例[21]进行仿真测试.其中,选取的Toy问题[15,22]和Kit问题[15,23]算例均为较难求解的约束优化问题,二者局部和全局最优解均位于可行域边界上且非凸.

当q=1时,CEIC策略变为经典的CEI策略.因此,针对单点填充,选取q=1 的CEI 策略,MS&CA 策略[15],验证所提CMIC策略单点填充的有效性及解的质量特性.当q ＞1进行多点填充策略比较时,选取具有代表性的Ginsbourger等提出采用预测均值μˆy作为伪值的Kriging Believer策略[13];张建侠等[15]提出的Pareto 选点MS&CA 策略.4种策略比较验证CMIC及CEIC多点填充策略的有效性及解的质量特性.因此,选择CMIC及CEIC多点填充策略进行昂贵约束并行代理优化的同时与Kriging Believer策略,MS&CA 策略优化结果进行比较.为便于书写及对Jones等人开创性工作的贡献,本文后续部分将Kriging Believer策略简记为q-EI&PoF;3 种单点填充的代理优化算法简记为CEI-EGO,CMIC-EGO及MS&CA-EGO.

5.1 数学算例

算例1 玩具问题(toy problem)包含两个约束条件(见图1),其全局最优解(红色实心圆点)为x* ≈(0.1954,0.4044),对应的最优响应值为0.5998.此外,算例1在试验点x ≈(0,0.75)和x ≈(07197,0.1411)处存在两个局部极小值(红色星点).

图1 玩具问题及其局部极小与全局最小值Fig.1 Local minimum and global minimum of toy problem

算例2Kit问题包含两个约束条件(见图2),其全局最优解(红色实心圆点)为x* ≈(0.2016,0.83332),对应的目标最优响应值为-0.7484.另,算例2存在局部极小值(红色星点)x ≈(0.2623,0.1223).

图2 Kit问题及其局部极小与全局最小值Fig.2 Local minimum and global minimum of Kit problem

5.2 工程案例

航空减速器(speed reducer design,SRD)设计优化问题.考虑齿轮齿根弯曲强度和齿面接触强度约束,轴的横向变形及轴的应力约束等共11个约束条件,对齿面啮合度b,大齿轮模数n,小齿轮模数m,轴承间距l1和l2及小齿轮直径d1,大齿轮直径d2共7个参数进行优化设计.以最小化齿轮箱的总重量为优化目标,见结构简图3.

图3 减速器设计问题Fig.3 Speed reducer design problem

5.3 试验参数设定

为了更好的验证所提算法的有效性及具体质量特性,所有优化过程及仿真测试均在Intel(R)Pentium(R)处理器、4 GB内存、2.90 GHz、Windows7 32位电脑操作系统下进行.文中算法涉及相关程序的实现代码均在MATLAB2015b软件上实现,其中Kriging模型实现选取DACE程序包执行[24].MS&CA程序相关代码实现在R软件实现,其中Kriging模型实现选取DiceKriging程序包实现[25].

初始试验设计过程中为避免在非可行域范围内选取过多的试验点,选取文献[15]样本方案设定初始试验设计样本量为5d.采用最大最小拉丁抽样方法进行初始试验设计,随机抽取30组初始试验方案进行优化以减少初始试验设计对试验结果的影响;优化过程中,设定优化算法循环的最大次数t=100为终止条件,最大估计次数为t×q+5d,并以30次随机优化结果的平均值作为算法稳健性能比较的依据;新试验点选取过程中,选取差分进化算法并设定种群规模Np=100,进化代数TG=200对均值改进填充策略进行优化.此外,分别设定近似全局响应最小值与已知响应最小值ymin的1%,1.5%绝对值误差百分比(absolute error percentage,AEP)作为终止条件,评估算法的收敛速度,收敛精度.

5.4 仿真结果分析

首先,选择CMIC 单点填充设计策略,MS&CA 策略和CEI策略对上述例子进行单点填充设计并对优化结果进行比较.其中,MS&CA策略兼顾可行边界的刻画与目标函数的期望改进进行填充;CMIC策略侧重于最大均值改进处进行加点而CEI策略侧重于最大期望改进处进行填充,二者均将可行性概率作为改进策略的权重来实现目标和约束的同时优化.设定最大昂贵估计次数Tm=50作为终止条件,最大最小拉丁超立方抽样设计下抽取5d个初始样本.在3种策略下分别重复进行30组随机试验,以30次试验获取3个算例优化估计的最终近似优化解ymin的平均值和标准差进行对比分析.具体结果见表1.

表1 单点填充ymin结果比较Table 1 Comparison of ymin in single point results

从表1结果可以看出,3种策略在单点填充时均可获得近似最优响应值.Toy和Kit问题最终优化响应值的均值和方差结果表明:对于变量数目较少的Toy问题和Kit问题,CMIC单点策略相比MS&CA策略及CEI策略具有更强的寻优能力且获取近似最优响应值稳健性更好.但在处理变量数目较多的SRD问题时,3种策略均可获得近似最优解,但CEI策略寻优能力最强且获取近似最优响应值更稳健.从仿真算例在3种单点填充策略作用下的整体优化结果来看:CMIC策略在处理变量数目较少问题时更具有优势,CEI策略则在多变量问题上更具优势,MS&CA策略对3种问题均可获得较为理想的优化结果,但其获取Pareto解集后单点选择运算效率较低;此外,上述所有测试案例最终优化结果均满足1%的绝对值误差百分比范围,可用于实际问题.在3种策略进行单点填充时,针对CMIC策略,CEIC策略处理不同问题上存在的优势,考虑MS&CA策略兼具目标改进与可行边界刻画的能力.后续通过选取4中策略对仿真测试案例进行多点填充的优化结果进行比较分析.

为了更好的比较3种策略在单点填充时的收敛速度,将3 种仿真案例分别在CMIC策略,MS&CA策略及CEI策略的仿真优化试验结果进行统计分析.选择获取试验结果中的最优响应值每隔10个点取一个值,绘制3种策略下30次随机试验的平均最优响应值随迭代次数变化收敛曲线,具体结果见图4.

图4 MS&CA-EGO,CMIC-EGO及CEI-EGO算法优化结果比较Fig.4 Comparison of MS&CA-EGO,CMIC-EGO and CEI-EGO algorithm optimization results

通过图4可以看出,Toy和Kit算例在3种策略进行填充设计时,CMIC策略收敛速度最快.SRD算例中3种填充策略收敛速度相近,均可以收敛到一种最优响应值附近.图4与表1结果表明:在变量数较少时,CMIC 策略更具优势;变量数目较多时,3种策略结果相近,但CEI策略更优.从3种策略作用下的昂贵约束代理优化算法的寻优结果可以看出:CMIC策略加点均选择在均值改进增量最大处进行加点,变量数目较少时收敛速度较快;MS&CA策略的Pareto最优解集挑选特性缩小了新试验点的选择范围,可实现有目的性加点;CEI策略寻优基于所有未知样本点近似响应的期望改进值进行填充,可以更好的兼顾探索空间.仿真试验优化结果与理论相符合.

单点填充策略往往采取最大化改进策略值处进行加点,策略成功获取改进的同时导致优化过程因贪婪特性而陷入局部最优解.为了更好的说明该特性,以Toy和Kit算例在CMIC和CEI两种单点策略指导下的优化填充设计效果进行分析,具体结果见图5.为对结果进行区分,选取蓝色上三角形作为初始试验设计样本点,红色圆点为新增样本点,其添加顺序用数字进行标记,具体顺序见图5-6.

图5 CMIC-EGO和CEI-EGO算法Toy问题优化结果比较(t=20,q=1)Fig.5 Comparison of CMIC-EGO and CEI-EGO algorithm optimization results(t=20,q=1)

通过图5-6中采用CEI策略与CMIC策略在单次增加1个点,增加20个新样本点获得样本空间分布与图1-2中全局最优解分布比较可以看出:1)两种策略指导下的代理优化算法填充20个点均可获得Toy及Kit问题的近似最优响应值;2)CEI策略及CMIC策略填充样本点位置相似,均可以实现在可行区域内的快速收敛.例如:Toy 问题填充的第1,2,3,4,5个样本点,Kit问题中的第1,5(6)点;3)两种策略在填充20个样本点条件下,均不能有效获得Toy和Kit问题的局部最优解;4)Toy问题中两种策略在添加第4个样本点时收敛到近似最优响应值附近,但第5,6个样本点均在点4附近添加,当代理模型近似波动幅度较大时易陷入局部最优;Kit问题中两种策略在添加第一个样本点可以收敛到全局最优解附近,CEI策略的期望填充可较好的实现可行域及空间内的覆盖填充;CMIC策略则多集中在可行域外部附近进行填充,部分添加样本点与CEI 策略填充位置相近.

相比于串行单点填充策略计算效率低下及填充策略的贪婪特性,CMIC和CEIC多点填充策略的优势在于保证初始均值或期望值最大化的同时,利用控制函数来实现改进增量I(x)的逐步减少.

为了更好的说明和比较所提并行代理优化算法的优化能力,选取q-EI&PoF策略、MS&CA策略与所提多点填充策略对Toy和Kit问题进行优化比较.设定初始试验参数:最大最小拉丁超立方抽取样本数为5d,单次循环新增q=4个新试验点,循环次数t=5,最大估计次数为5d+5q.绘制新增样本点在设计空间内填充位置的等高线图进行比较,具体填充结果见图7-8.

图8 4种并行代理优化算法Kit问题结果比较(t=5,q=4)Fig.8 Comparison of four parallel surrogate-based optimization algorithm results in Kit problem(t=5,q=4)

由图7-8关于Toy问题及Kit问题优化后的样本空间分布可以看出:1)4种并行代理优化算法均能获得Toy及Kit问题的全局最优解,但q-EI&PoF策略作用下解的精度较差;2)采用4种策略的并行优化算法只需少量迭代就可获得较高精度的近似最优解,有助于计算效率的提升;3)q-EI&PoF 策略获取多个新试验点聚集在非最优区域,优化精度及计算效率不高;4)MS&CA策略在单点填充时,获得近似最优解的同时兼顾约束边界,获取的近似最优解在最优可行域集中度较高,优化效率及精度较高;5)CEIC与CMIC策略的样本填充顺序类似,近似最优解可以实现在最优可行域附近聚集填充,具有较高的优化精度及计算效率;与q-EI&PoF和MS&CA策略优化结果比较,CEIC与CMIC策略对于Toy问题可获得一个局部最优解,对于Kit问题获得2个局部最优解.表明CEIC与CMIC策略具有更好的全局搜索特性.

昂贵优化算法优化效率的提升及成本降低主要来源于昂贵估计仿真次数的减少.设定终止条件为AEP＜1.5%,重复进行30次随机试验并统计算法终止时的平均迭代次数,最大迭代次数来估计所提算法优化效率.选取CEIC和CMIC策略一次增加q=3个样本点对Toy及Kit问题进行优化,并与张建侠等[15]优化结果进行比较.具体结果见表2.

从表2中30次随机试验优化数据统计结果可以看出:在AEP＜1.5%终止条件下,一次增加3个新试验点的4种多点填充均以较快速度收敛到1.5%精度以内,表明4种策略作用下的并行代理优化算法获取优化解具有较高精度,在处理昂贵黑箱约束问题有效且均能满足设计要求;4种多点填充策略的迭代次数和昂贵估计仿真试验次数均少于CEI单点填充设计方案,表明多点填充相比单点填充设计更高效,通过计算机的并行计算可有效提升工程优化效率;并行代理优化过程中迭代次数和昂贵估计仿真试验次数的减少,有助于优化效率的提升及成本降低.在初始设计样本量相同条件下,并行代理优化算法在CEIC及CMIC多点填充策略作用下对Toy和Kit问题优化效率的提升优于q-EI&PoF和MS&CA策略;基于控制函数进行均值改进控制的CEIC及CMIC多点填充策略,可实现对样本设计空间的高效填充,有助于提升并行代理优化算法的优化效率及收敛精度.

表2 不同算法1.5%绝对误差百分比优化效率比较Table 2 Efficiency comparison of 1.5%absolute error percentage with different algorithms

对比图5-8 结果可以发现:CMIC和CEIC两种多点填充策略收敛到最优解附近的解的数量基本一致,对比新增样本点的空间分布发现,两种填充策略搜索下新增试验点分布类似,说明CMIC可在某种程度上取代CEIC策略甚至优于CEIC策略;对于Toy及Kit问题,CEIC新增试验点空间分布较为均匀,相较CEIC策略新增样本点更集中且在可行域边界样本数量更多,说明CMIC策略在变量个数较少时边界搜索能力更强.

基于Kriging模型的昂贵约束并行代理优化算法计算效率提升的关键是多点填充策略的选择,提升程度则取决于优化过程中单次循环新增试验点的个数q.随着新增试验点q的增多,计算效率提升程度逐渐增高是并行代理优化算法的效率目标.因此,选取MS&CA策略,q-EI&PoF 策略与基于均值控制的CMIC,CEIC 多点填充策略在单次循环迭代中分别增加q=1,2,4,6,8,10个新试验点.以AEP＜1%作为终止条件,选取30次随机试验优化结果中迭代次数的平均值及标准差作为优化效率指标进行比较分析.具体统计结果见表3.

表3 1%绝对值误差百分比条件下最大优化迭代次数均值(方差)统计结果比较Table 3 Comparison of statistical results of mean(variance)of maximum optimization iterations under the condition of 1%absolute error percentage

表3是3种算例在4种多点填充策略作用下,一次增加q个样本点的终止迭代次数t的均值和标准差进行统计结果.从表3可以看出:1)4种多点填充策略在AEP＜1%条件下,相比单点(q=1)填充策略均实现了代理优化效率的提升,可有效减少仿真计算成本;2)对于Toy问题,q-EI&PoF 随着q个数的增多,当q ＞4时优化效率提升不明显;CMIC策略在q ＜4时,优化效率提升弱于MS&CA和CEIC 填充策略;3) 对于Kit 问题,4 种多点填充策略差别不大,但CEIC及CMIC填充策略优于另外两种策略;4)对于SRD问题,可以看出CMIC策略在一次增加样本点个数较少时,优化效率弱于其余3种策略.但随着q的增加可以看出,CMIC策略与其余3种策略的差距越来越小,表明CMIC策略相比单点填充设计更适用于多点填充.上述研究结果表明:基于均值改进控制函数发展的CEIC及CMIC多点填充策略,其均值改进控制机理可有效提升算法优化效率,实现样本设计空间的高效填充.

6 结论与展望

文章基于改进增量及新增样本点的不等关系,提出了均值改进控制函数概念并给出了理论分析;针对昂贵约束优化问题,基于约束均值改进策略提出了CMIC-PSBO及CEIC-PSBO算法.测试结果表明:所提算法可有效获得昂贵约束优化问题的近似最优解,且精度较高;基于均值改进控制的多点填充策略适用于并行计算,可有效减少昂贵仿真次数实现并提升计算效率.此外,Zhan等人构建了影响力函数对EI策略施加影响[14],其原理与均值改进控制函数原理相同,但未给出具体的理论分析与证明.因此,关于增量控制函数的理论分析与证明过程可解释其影响力函数的作用性质与结果.同时均值改进控制策略也对现有改进填充策略的贪婪特性有一定的启发意义.

现有针对具有黑箱特性的昂贵优化问题多是基于最大改进I(x)发展而来.因此,更多的控制函数的发现及将均值改进控制函数应用到更多的空间填充设计策略是值得研究的方向.此外,将该方法应用到多目标优化问题也是可以尝试的课题.