多阶邻接分布熵下的复杂网络节点相似性分析方法
王小刚,闫光辉,周 宁
(兰州交通大学电子与信息工程学院,甘肃兰州 730070)
1 引言
复杂网络是基于图论的复杂系统建模方式,已成为涉及自然科学、社会科学和工程学等诸多邻域的重要交叉研究课题[1-4].复杂网络研究一般基于某些量化的结构或动力学特性,如度分布、模块度、相似性、中心性、随机游走等[5-9].而复杂网络的结构呈现出各种复杂、异构甚至是无序和不确定的情况[10],需要多样性的网络或节点结构信息度量和分析方式.
信息熵[11]作为度量复杂网络结构的有力工具近些年日益受到重视.复杂网络结构熵基于一定的结构量定义熵,如文献[1]中给出基于度序列分布的熵,可以用来评价网络总体的规则性,熵越高网络越随机;文献[12]给出的Wu熵基于节点度衡量节点分布均匀程度,熵越大网络越均匀;文献[13]提出介数熵描述权重网络的结构特性,比度熵能更有效地描述有权复杂网络结构信息;文献[14-15]基于节点最短路径定义距离熵,并讨论了极值情况,有助于研究网络的构造特性.另外,学者也从复杂网络的代数特征和动力学特征出发定义和研究结构熵,如文献[16-17]基于拉普拉斯矩阵的特征值定义熵,通过分析节点移除导致的熵值变化,度量异构性及节点重要性,可以有效发现网络中的关键结构特征;文献[18]基于指数邻接矩阵定义游走熵,有助于揭示网络的动力学特性;文献[19]基于树结构和随机游走定义复杂网络高维熵,以表示和检测复杂网络的真实结构.
以上提到的熵都是宏观熵.宏观熵针对整个网络,度量某种结构量的总体分布特性[20].与之相对应的是节点微观熵,一般用来表示节点的局部结构信息,如文献[21]给出基于节点与其他节点最短距离分布的熵,从而发现中心节点;文献[22]提出一种基于邻域度分布的节点熵,用于节点相似性评价.目前文献中已有的复杂网络结构熵主要是宏观熵,微观熵比较少.宏观熵关注网络整体结构信息忽略局部,而现有微观熵主要基于邻域交互和最短距离,局限性较大,需要一种节点熵能从更灵活尺度上度量节点多层邻居的分布特征.
基于节点熵可以构造相对熵来对比节点间的相似性[22-23].节点相似性是重要的结构特征,有很多重要的用途,如社区检测、链路预测、节点分类.常见的相似性方法有:
1)基于共同邻居的方法[8,24],一般采用节点对之间公共邻居的数目,公共邻居的度等结构信息进行相似性计算,如JACCARD算法,共同邻居算法.这种方法计算简单,但只考虑了浅层局部的信息;2)基于路径的方法[8,24],考虑两个节点的路径连接来计算相似性,包括基于局部路径的算法如局部路径(local path,LP)算法和全局路径的算法如KATZ.基于路径的方法容易使大度或大介数节点成为一般节点的相似节点.全局路径算法考虑整个网络结构及路径,当规模很大时,难以计算,一般使用具有少量阶数的局部路径算法;3)基于随机游走的方法[8],此类算法根据节点间游走时间或到达概率等特性建立相似性模型,有全局随机游走算法如平均通勤时间(average commute time,ACT)算法和局部性游走算法如迭代随机游走(superposed random walk,SRW)算法;在大型网络上全局游走算法复杂度太高,实际上多使用局部随机游走算法;但局部游走算法受最短路径等结构元素影响较大.和基于路径的方法类似,这种方法也会使大度节点成为一般性相似节点;4)基于节点结构相对熵的方法,这类方法通过对比节点间某种结构量的分布一致性程度计算相似性.目前这种方法比较少,文献[22]提出一种基于邻域度分布的局部相对熵(local relative entropy,LRE)的相似性度量方法,文献[23]基于节点距离分布相对熵(distance distribution relative entropy,DDRE)研究节点间的相似性.LRE只是考虑了邻域节点的度信息相似性,DDRE只考虑了最短路径.这些都没有考虑多阶邻居分布特征下的节点相似性.
本文提出一种节点的多阶邻接分布熵(multi-layer adjacency entropy,MAE),用于度量节点多阶邻居的分布信息,提供研究节点和网络结构特征的一种中观视角:对任意节点,选取合适的阶数k,避免过于庞大复杂的计算,又不局限于浅层,得到一定尺度下节点周边结构特征的一种信息表示.进而定义多阶邻接分布相对熵(multi-layer adjacency relative entropy,MARE),研究基于相对熵的节点相似性.
2 多阶邻接分布熵
多阶邻接分布熵(MAE)是一种节点局部熵,度量节点k阶内邻居节点在各阶上的分布特征信息,以下给出MAE相关的定义和定理.
令G(V,E)为无向复杂网络,V是节点集合,E是边集合,n是节点个数.
定义1i,j ∈V,d(i,j)表示i到j的最短距离.定义
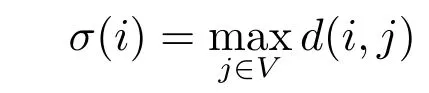
为节点i的离心率,
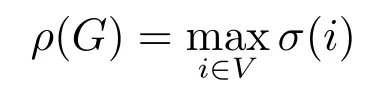
为G的直径,
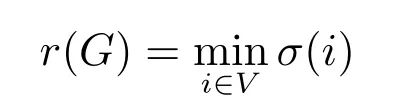
为G的半径[25].
定义2i,j ∈V,定义与i相距为k的节点数为

其中:若d(i,j)=k,则有δ(d(i,j)=k)=1,否则δ(d(i,j)=k)=0.当k=0时,令=1,表示节点0步可达自身.
定义3={j|d(i,j)=k,j ∈V}表示与节点i最短路径为k的所有节点集合,集合中的节点称为i的k阶邻居.
定义4定义节点i的多阶邻接分布熵(MAE)为

其中:log是以2为底的对数,k是阶数.MAE是一种香农信息熵.
定义5相对熵用于衡量两个随机分布p(x)和q(x)的差距,其基本定义为j的k阶MAE相对熵(MARE)如下:

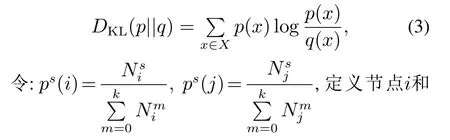
定理2对于节点i,当k >σ(i)时,节点的熵不再增大,即节点的MAE熵在离心率处收敛;当k >ρ(G)时网络的任何节点熵不再增大,即网络的MAE熵在其直径处收敛.

2) 当k >ρ(G),对于所有节点i ∈V,必有k >σ(i). 证毕.
定义6由定义1和定理2,对v ∈V,称离心率σ(v)为节点v最大MAE影响力尺度;称直径ρ(G)为网络的最大MAE影响力尺度.
定理3对于k阶MAE熵,孤立节点的熵最小,值为0;1到k阶分布节点数完全均匀时节点MAE熵达到最大值,最大值为

3 计算MAE熵基本算法


4 网络节点相似性指标
4.1 互相似性指标
基于MAE相对熵,在尺度k下对比两个节点的局部结构相似性.相对熵越小,两个节点越相似.如果i以j为最相似节点,那么j也应视i为最相似节点.一个节点可以和多个节点相似.设Φi是节点i视为最相似的节点集合,即有
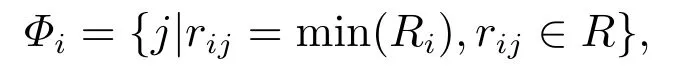
R是相对熵矩阵,其元素rij是节点i对j的相对熵,Ri是i对网络节点1,···,n的相对熵组成的向量.若i ∈Φj,且j ∈Φi,则i,j互为最相似,
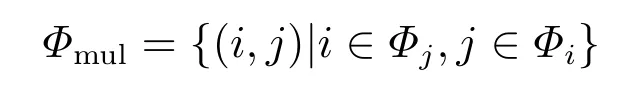
是互最相似对节点集合.定义互相似性指标为
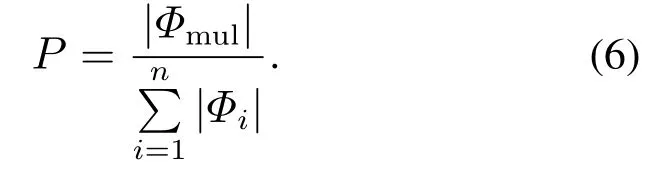
4.2 传播影响力
如果节点相似,其传播影响力也应该相似[22-23],可以采用SIR模型[26]来进行验证.在SIR模型中,节点分为3种状态:易感状态(I),节点未被感染,可能会变成感染状态;感染状态(U),节点已被感染,可以传染疾病;免疫状态(R),结点不会再传染,也不再被感染.
步骤1分别计算以每个节点作为传播源(U),其他节点易传染(I)的状态下,按一定概率传染100步每步网络节点的感染率指i节点作为传染源第t步网络感染率,t ∈[1,2,···,100].
步骤2计算所有互最相似节点对之间每步感染率差值的绝对值之和t ∈[1,2,···,100].
步骤3得到
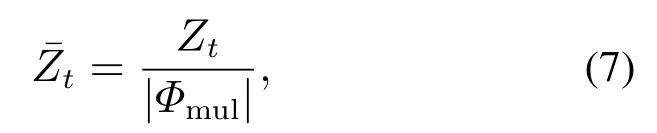
5 实验和分析
实验用网络数据集中Sw,Sf,Rm由程序生成,其余数据集来自http://konect.uni-koblenz.de/networks/,见表1所示.

表1 网络数据集Table 1 Network datasets
5.1 互相似指标分析
由定理2,当k >ρ(G)时,所有节点的熵不再增加,一般应取k≤ρ(G).对于尺度t的选取,取决于需要在多大的尺度上考察节点的相似性.表2是在5阶尺度下MARE与LRE[22],JACCARD,KATZ[8]几种方法互相似指标对比.通过表2,可以看出基于MARE相对熵的相似性方法取得了较好的相似比.所有10个网络中,MARE 互相似比超过了KATZ.除了Karate网络的9个网络上,MARE互相似比超过了JACCARD.在Jazz,Polbooks,Dolphins,Astroph,Rm和Sw这6个网络上,MARE 的运行结果好于LRE;在Chicago 和Egofacebook网络上MARE和LRE方法互相似比一样;仅在Karate和SF上,MARE熵互相似性指标不如LRE,这是因为网络结构特征不同,而每一种相似性方法体现了一定的结构比较角度,并无绝对优劣之分.在后面的传播影响力指标实验上,MARE在所有网络上表现比LRE更好.
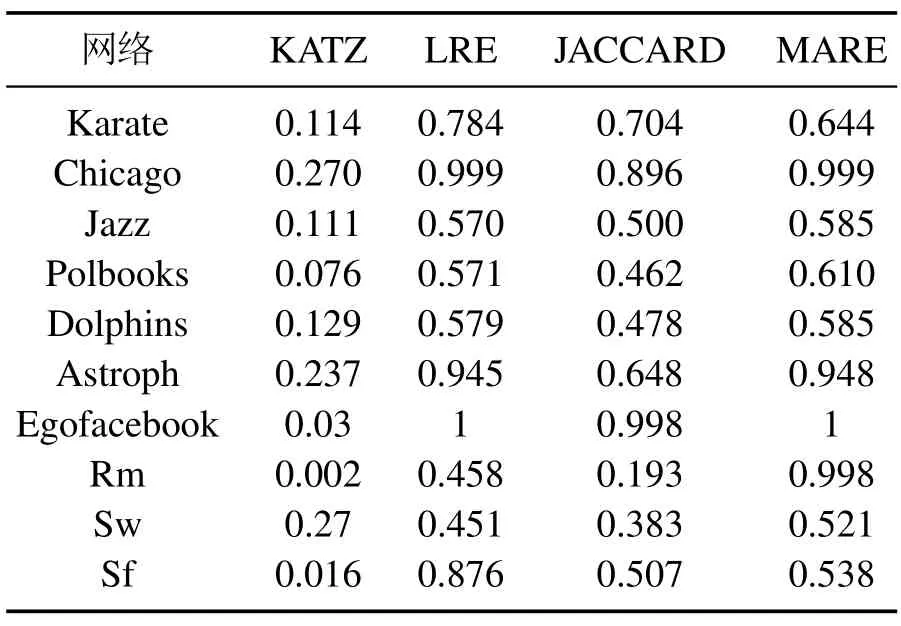
表2 互相似比Table 2 Mutual similarity ratio
设MARE相对熵矩阵为R,其元素rij为节点i对节点j的相对熵,根据相对熵的定义,R不对称.令H=R+RT,则H为对称矩阵,hij为H中元素,通过hij=1-hij/max(hij),归一化每个元素,得到标准化的相似性矩阵,其值在[0,1]之间.1为完全相似,0为完全不相似.LRE相对熵矩阵做同样对称化和归一化处理.JACCARD相似性矩阵和KATZ相似性矩阵进行同样的归一化处理.
下面基于相似性矩阵绘制热力图(图1),直观地看一下Jazz网络的相似性.图1热力图坐标为节点标号,体现节点间的相似性程度.可以看出,Jazz网络如果基于KATZ 方法度量,总体上节点之间相似性较低,JACCARD方法下相似性状况比KATZ要好些,LRE方法下相似性更好些,很多节点间的相似性值超过了0.8,MAE 熵视角下节点间相似程度最高,可以说在MAE熵视角下该网络同构性很高.
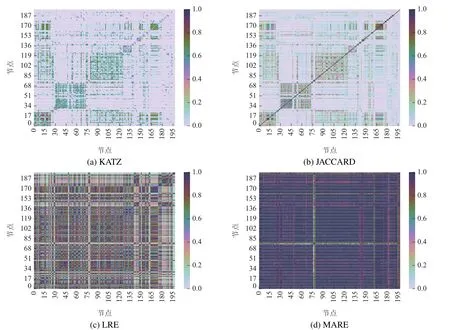
图1 Jazz网络相似性热力图Fig.1 Similarity heat map of Jazz
下面以Jazz网络和Chicago为例,给出几种相似性方法的相似性散点图,横坐标和纵坐标都为节点编号,每个横坐标节点和其对应的最相似点为一散点.从全局性相似性度量的角度考虑的话,散点应该分散在二维平面上,而不是集中于对角线附近或堆在局部.如果节点a以b为最相似,b也应识别a为最相似点,体现在图上就是对称.
图2 是Jazz 网络4 种相似性散点图,可以看出,MARE方法具有较好的对称性,说明该指标较好地衡量了相似性.JACCARD方法基于共同邻居衡量相似性,相似节点集中在每个节点的附近,所以主要沿对角线聚集.KATZ是基于路径的相似性,度大的节点处在多个路径的可能性更多,与较多或者大多节点相似的概率更大[23],Jazz 度最大的5 个节点依次是[66,6,19,22,89],这个在图2(c)中得到了体现.
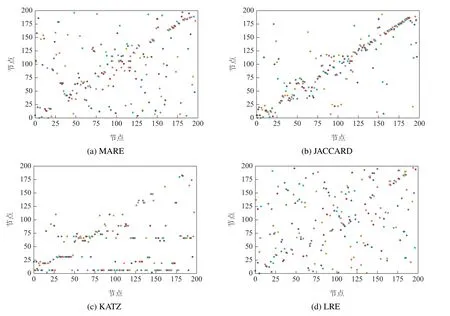
图2 Jazz网络节点互最相似散点图Fig.2 Scatter diagram of most similar nodes in Jazz
图3是Chicago网络4种相似性散点图.Chicago网络度分布相对均匀,没有特别大度的节点.而此网络有一些介数很大的节点,介数排前5 的节点标号为[1155,1156,1146,1154,1152],介数依次为[251953,209291,93440,90713,88642],意味着很多路径通过这些节点,所以在KATZ方法中被很多节点视为最相似,在图3(c)中体现为一条横线.JACCARD和KATZ两种方法相似,介数较大的点都与其他点相似得更多,但这个效果KATZ体现得更明显.该网络的LRE相似性对称强,因网络中有大量度相同的节点,按照LRE方法易被判为相似节点,所以在图3(d)中体现为很密集的散点图.图3(a)体现了MARE方法下Chicago网络整体很强的相似对称性,同时又避免了很多同度节点造成的片面相似性.

图3 Chicago网络节点互最相似散点图Fig.3 Scatter diagram of most similar nodes in Chicago
5.2 互相似节点传播分析
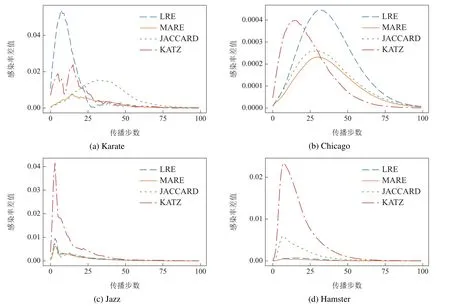

图4 互最相似节点各步感染率差值Fig.4 Variance of infection probability of mutual most similar nodes in networks
6 结束语
熵可以度量复杂网络节点的结构信息,本文提出节点的多阶邻接分布熵,用于表示k阶内邻居节点的分布特征,熵越高,说明分布越均衡,反之越不均衡.随着阶数k增大,节点的MAE熵也增大,并在离心率处收敛,k增大到网络的直径时,所有节点的MAE熵不再增加,即网络的MAE熵收敛.MAE熵代表的节点多阶邻居分布状态提供一种新的角度分析节点间相似性和网络整体的异构性.通过定义相应的多阶邻居分布相对熵,度量节点之间的相似性.实验表明这种度量方式效果明显,具有较好的互相似比;通过疾病传播模型,以这种方式度量的互最相似节点传播感染率平均差距最小,说明是一种合理有效的节点相似性度量方式.

